1. 概要
- その3(https://qiita.com/asys/items/9d40172e72dd01caa293)に引き続いて『経済・ファイナンスデータの計量時系列分析』を元に勉強中。
- 今回は4章に当たる部分、VARモデルについて。
2. VARモデルとは
- VARモデルとはARモデル多変量に拡張したもの。
- $VAR(p) : \mathbb{y}_t=\mathbb{c}+ \Phi _1 \mathbb{y} _{t-1} + \cdots + \Phi _1 \mathbb{y} _{t-p} + \epsilon _t, \quad \epsilon _t \sim W.N.(\Sigma)$
- 式を見れば分かるように、同時点での他の変数が含まれていない点に特徴がある。
- 常定条件は以下のAR特性方程式の全ての解の絶対値が1より大きくなることである。
$|\mathbb{I} _n - \Phi _1 z - \cdots - \Phi _p z^p|=0$
ただし、$\mathbb{I} _n$は$n\times n$の単位行列である。 - モデルの推定については、OLSによって各方程式を個別に推定してやればよく、ARモデルの推定と同じ方法で推定が可能である。
3. グレンジャー因果性
定義
- 変数同士の因果関係について、データだけから因果性の有無を判断できるよう考案されたのがグレンジャー因果性である。
- $\mathbb{x}_t$について、時点$t$において利用可能な情報の集合を$\Omega _t$、$\Omega _t$から$\mathbb{y} _t$を取り除いたものを$\tilde{\Omega} _t$とする。$\tilde{\Omega} _t$に基づく将来の$\mathbb{x}$の予測のMSEよりも、$\Omega _t$ に基づくMSEの方が小さくなる時、$\mathbb{y} _t$から$\mathbb{x} _t$へのグレンジャー因果性が存在する。
- 言い換えると、$\mathbb{x} _t$の予測にあたって$\mathbb{y} _t$の情報が予測精度を向上させる場合、因果性が存在するということである。
- グレンジャー因果性は通常の意味での因果性が存在するための必要条件であるが、十分条件ではない。
検定
- $\Omega _t$を用いた推定の残差平方和を$SSR _1$とし、$\tilde{\Omega} _t$による推定の残差平方和を$SSR _0$とする。
- $F$統計量を以下のように計算する。ただし、$r$は検定に必要な制約の数である。
$F \equiv \frac{\frac{(SSR_0-SSR_1)}{r}}{\frac{SSR_1}{(T-np-1)}}$ - $rF$は漸近的に$\chi^2(r)$に従うことが知られており、これを用いてグレンジャー因果性を判定する。
分析例
データ
- データはFI2010というデータセットを使用した。ここからData AvailabilityのところにあるAccess this dataset freely.をクリックすればダウンロードできる。
- ここでは詳細は省くが、株の取引所における板情報のデータセットとなっている。今後個人的に触っていきたいデータセットなので慣れるために使用した。
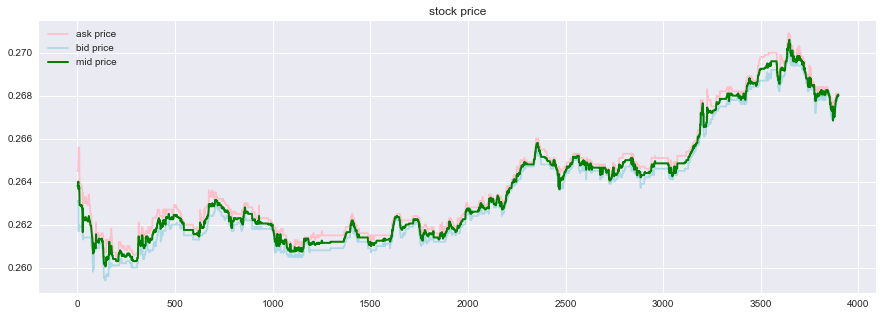
- ここでは株価の推移(以下中値の変化率)と最良気配数量の不均衡度合いを分析する。ある時点での最良気配数量について、BIDの方が多ければ買い手の方が売り手よりも多いと考えられ、これが将来の株価上昇につながるのではないかとの推測による。
前処理
# データの読み込み。
data = pd.read_csv('Train_Dst_Auction_DecPre_CF_1.txt', header=None, delim_whitespace=True)
# 最初の4行が最良ASK/BIDについての価格と数量のデータになっている。
# また、最初の3900列程度が1つ目の銘柄についてのデータとなっている。
pr = data.iloc[:4,:3900].T
pr.columns = ['ask_p','ask_v','bid_p','bid_v']
# 最良ASKと最良BIDから中値を計算する。
pr['mid_p'] = (pr['ask_p'] + pr['bid_p']) / 2
# 中値の変化率を計算する。
pr['p_chg'] = pr['mid_p'].pct_change()
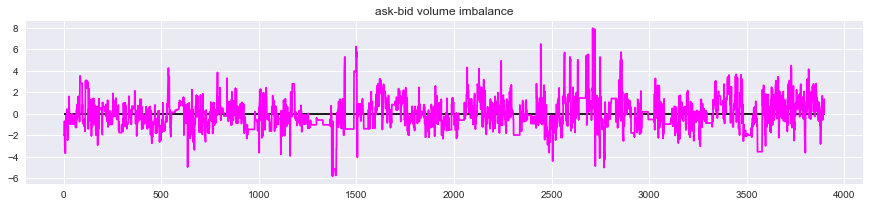
# ASKとBIDの数量の不均衡度合いを計算する。
pr['v_imb'] = (pr['ask_v'] / pr['bid_v']).apply(np.log)
pr = pr.dropna()
-
なお、最良気配数量の不均衡度合いについては、
$\qquad Imbalance=\ln \frac{V_{ask}}{V_{bid}}$
として算出しており、値が正の場合売り数量の方が多く、値が負の場合は買い数量の方が多いことを表している。 -
1つ前の時点で不均衡度合いの値が正で売り数量の方が多い場合、現時点で株価が下落しているかどうかを簡単に確かめてみる。
# 前の時点で売りの方が多いケース
print('sell > buy ', pr.loc[pr['v_imb'].shift(-1)>1, 'p_chg'].sum())
# 前の時点で買いの方が多いケース
print('sell < buy ', pr.loc[pr['v_imb'].shift(-1)<1, 'p_chg'].sum())
# sell > buy -0.0060484707428217765
# sell < buy 0.027729879129729684
- という具合で一応平均的には売りが多い場合中値は下落、買いが多い場合は中値が上昇していると言えなくもない状況である。
グレンジャー因果性の検定
- 毎度おなじみのstatsmodelsを使用する。
# まずはライブラリを読み込み、データをフィードする。
from statsmodels.tsa.vector_ar.var_model import VAR
model = VAR(pr[['v_imb','p_chg']].values)
- 次にモデルの次数を決定します。VAR(p)のpにあたる値です。これもライブラリを使えば一発。
model.select_order(10).summary()
| AIC | BIC | FPE | HQIC | |
|---|---|---|---|---|
| 0 | -15.49 | -15.48 | 1.880e-07 | -15.49 |
| 1 | -16.29 | -16.28 | 8.405e-08 | -16.29 |
| 2 | -16.31 | -16.30 | 8.217e-08 | -16.31 |
| 3 | -16.32 | -16.30 | 8.173e-08 | -16.31 |
| 4 | -16.33* | -16.30* | 8.101e-08* | -16.32* |
| 5 | -16.33 | -16.29 | 8.103e-08 | -16.32 |
| 6 | -16.33 | -16.29 | 8.108e-08 | -16.31 |
| 7 | -16.33 | -16.28 | 8.112e-08 | -16.31 |
| 8 | -16.33 | -16.27 | 8.116e-08 | -16.31 |
| 9 | -16.33 | -16.27 | 8.111e-08 | -16.31 |
| 10 | -16.33 | -16.26 | 8.120e-08 | -16.30 |
- とりあえず次数10までを見たところ、デフォルトの4つの基準で見てどれも$p=4$がいいとしてきたため、次数は4に決定する。
- 次にグレンジャー因果性について見る。
# 次数を4としてモデルを作成する。
var_model = model.fit(4)
# グレンジャー因果性の検定。causing=0('v_imb')からcaused=1('p_chg')への因果性を検定する。
Granger = var_model.test_causality(causing=0, caused=1)
Granger.summary()
| Test statistic | Critical value | p-value | df |
|---|---|---|---|
| 9.531 | 2.373 | 0.000 | (4, 7772) |
- p-valueを見ると0.05よりも小さくなっているので、グレンジャー因果性が存在していると言える。やはり板の不均衡度合いがその後の株価の推移に影響を与えていそうである。
- ちなみに逆に株価の推移から板の不均衡度合いへの因果性を検定してみると以下のようになった。
Granger = var_model.test_causality(causing=1, caused=0)
Granger.summary()
| Test statistic | Critical value | p-value | df |
|---|---|---|---|
| 0.9424 | 2.373 | 0.438 | (4, 7772) |
- こちらはP値が0.05より大きくなっており、因果性は認められないという結果になった。株価が上昇することにより売り物が増えてくるなどの関係性が存在しそうなものだが、分析しているタイムスパンが短すぎることもあってか、グレンジャー因果性は存在していなかった。
4. インパルス応答関数(Impulse Response Function)
非直交化インパルス応答関数
- 一般的なVARモデルにおいて、$y_{jt}$の撹乱項$\epsilon_{jt}$に1単位のショックを与えた時のk期後の$y_{i,t+k}$の変化を関数としてみたもの。
- $IRF_{ij}(k)=\frac{\partial y_{i,t+k}}{\partial \epsilon_{jt}}$
- 撹乱項間に相関が存在しないことを前提としているが、現実には$\epsilon_{it}$と$\epsilon_{jt}$の間に相関が存在するケースも多く、このような場合をうまくモデル化できていない点が問題である。
直交化インパルス応答関数
- 撹乱項の分散共分散行列を三角分解し、互いに無相関な撹乱項に分解したのち、その撹乱項に1単位のショックを与えた時のインパルス関数。
- 一般的なVARモデルにおいて、
$\qquad VAR(p) : \mathbb{y}_t=\mathbb{c}+ \Phi _1 \mathbb{y} _{t-1} + \cdots + \Phi _1 \mathbb{y} _{t-p} + \epsilon _t, \quad \epsilon _t \sim W.N.(\Sigma) $
$ A $ を対角成分が1に等しい下三角行列、$D$を対角行列として、
$\qquad \Sigma=ADA'$
と三角分解し、
$\qquad u_t=A^{-1}\epsilon_t$
という形で直行化撹乱項$u_t$を得ることができる。 - $IRF_{ij}(k)=\frac{\partial y_{i,j+k}}{\partial u_{jt}}$
- 三角分解を用いていることから、$\epsilon_{kt}$は$u_{1t},\cdots,u_{kt}$の線形和となる。このため、変数の並び順が結果に影響を与えることとなる。
分析例
- グレンジャー因果性のところで用いた板データを引き続き使用していく。
# 次数を4としてモデルを作成する。
var_model = model.fit(4)
# k=10までのインパルス応答を計算する。
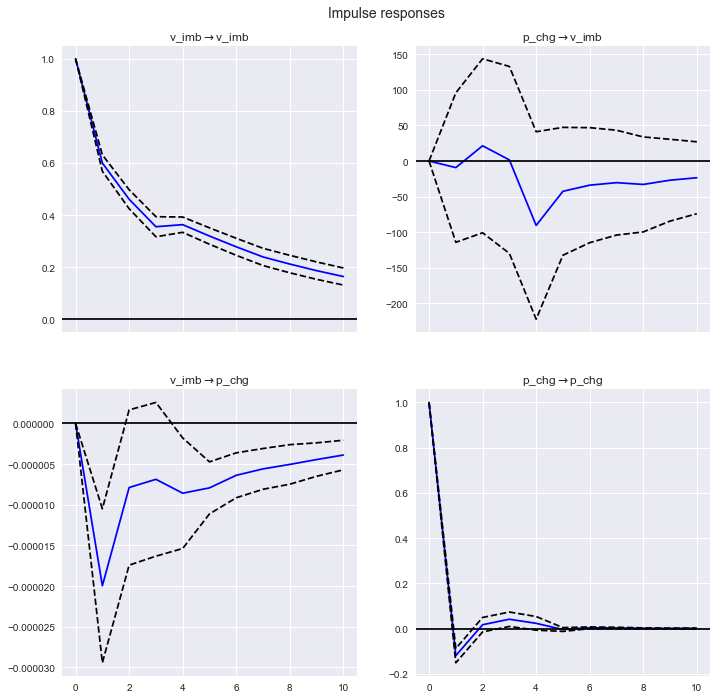
IRF = var_model.irf(10)
# 結果をプロットする。orth=Falseは非直交化を意味する。
IRF.plot(orth=False)
plt.show()
- 注目したいのは左下のv_imb→p_chgのインパルス応答である。1期後にマイナスの反応が出ており、その後反応が徐々に小さくなっている。不均衡度合いが1単位上昇するとそれは売りが増えたことを意味し、その後の株価のパフォーマンスとして下落がもたらされることが示唆されている。
5. 分散分解
定義
- $y_i$のk期先予測のMSEに対して、$y_j$の直行化撹乱項$u_{j,t+1},\cdots,u_{j,t+k}$が寄与する割合を相対的分散寄与率(RVC)と呼ぶ。
- n変量VARモデルについて、$y_i$のk期先予測のMSEは、$\mathbb{u}_{t+1},\cdots,\mathbb{u}_{t+k}$の線形和となるので、
$\qquad \hat{e}_{i,t+k|t}=\sum_{h=1}^{k}w_{1,t+h}^{i}u_{1,t+h}+\cdots+\sum_{h=1}^{k}w_{n,t+h}^{i}u_{n,t+h}$
とすると、
$\qquad MSE(y_{i,t+k|t})=\sum_{l=1}^{n}\sigma_l^2\sum_{l=1}^{k}(w_{l,t+h}^i)^2$
$\qquad where \quad \sigma_l^2=E(u_{lt}^2)$
を用いると、
$\qquad RVC_{ij}(k)=\frac{\sigma_j^2\sum_{h=1}^{k}(w_{j,t+h}^i)^2}{\sum_{l=1}^{n}\sigma_l^2\sum_{h=1}^{k}(w_{l,t+h}^i)^2}$
と表すことができる。
分析例
- 引き続きFI2010の板データを使用する。
# 次数を4としてモデルを作成する。
var_model = model.fit(4)
# k=10までの分散寄与率を計算する。
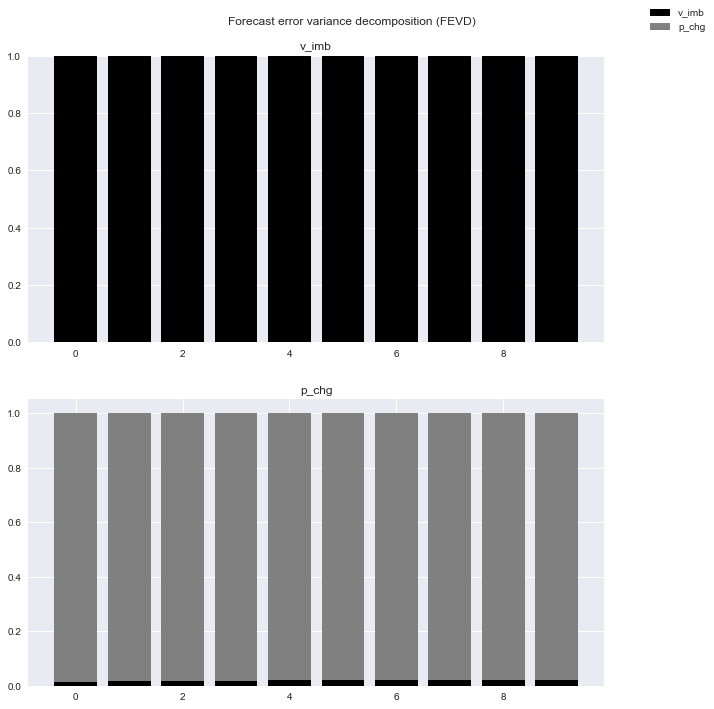
FEVD = var_model.fevd(10)
# 結果をプロットする。
FEVD.plot()
plt.show()
- これではあまりに分かりにくいので、具体的な数値を見てやる。
FEVD.summary()
| FEVD for v_imb | v_imb | p_chg |
|---|---|---|
| 0 | 1.000000 | 0.000000 |
| 1 | 0.999994 | 0.000006 |
| 2 | 0.999969 | 0.000031 |
| 3 | 0.999971 | 0.000029 |
| 4 | 0.999572 | 0.000428 |
| 5 | 0.999511 | 0.000489 |
| 6 | 0.999478 | 0.000522 |
| 7 | 0.999452 | 0.000548 |
| 8 | 0.999418 | 0.000582 |
| 9 | 0.999397 | 0.000603 |
| FEVD for p_chg | v_imb | p_chg |
|---|---|---|
| 0 | 0.012342 | 0.987658 |
| 1 | 0.018310 | 0.981690 |
| 2 | 0.018871 | 0.981129 |
| 3 | 0.019158 | 0.980842 |
| 4 | 0.019791 | 0.980209 |
| 5 | 0.020477 | 0.979523 |
| 6 | 0.020889 | 0.979111 |
| 7 | 0.021208 | 0.978792 |
| 8 | 0.021472 | 0.978528 |
| 9 | 0.021678 | 0.978322 |
- v_imbの分散に対するp_chgの寄与度は非常に低いことが分かるが、これはグレンジャー因果性やインパルス応答から見ても整合的である。
- 逆にp_chgに対してv_imbは2%程度の寄与をしている。この数値も非常に小さいが、予測期間が長くなるに従って寄与度が若干上昇しており、板状況の変化が株価に織り込まれるまで多少の時間を要する可能性を示唆している。