1. はじめに
文献[1]で、UCLK(Upper-Confidence Linear Kernel reinforcement learning)という強化学習のアルゴリズムが提案されました。UCLKを簡略化したアルゴリズム(以下、簡易版UCLK)と、ばねマスダンパ系を制御対象にした数値実験でアルゴリズムを検証した結果を、記事[2]で紹介しました。そこでは、状態遷移関数を、現時刻の状態と次時刻の状態の差が混合正規分布に従う確率分布に制限しました。
この記事では、系のダイナミクスをより広く表現できるように状態遷移関数を拡張したアルゴリズムを紹介します。次時刻の状態の確率分布は、記事[2]と同様に、混合正規分布で定義していますが、混合正規分布を構成する正規分布の中心を、現時刻の状態の線形結合および行動によって決まるベクトルの和とすることで、線形時不変システムを含むクラスで系のダイナミクスを表現できるようにしました。
ダイナミクスのクラスを拡張することで、どういった効果が得られるか、ばねマスダンパ系を制御対象とした数値実験を通して検証した結果を紹介します。
2. アルゴリズム
2.1. モデルと未知パラメータ
状態遷移関数のモデル
状態遷移関数を次のように定義しました。
p(s'|s,a) = \sum_{i=1\cdots d} \theta_{i,a} {\cal N}(s' | \bar{F}_{i}s + \bar{g}_{i}, \bar{\sigma}^2_{p} {\rm I}_{n} )
ただし、$s',s\in\mathbb{R}^{n}$は、それぞれ、次時刻および現時刻における状態で、$n$次元のベクトルとします。また、$a\in{1\cdots A}$は行動です。重み係数$(\theta_{i,a})_{i=1\cdots d,a=1\cdots A}$は未知パラメータで、データから学習します。${\cal N}(...)$は、$n$次元正規分布の確率密度関数です。$\bar{F}_{i}\in \mathbb{R}^{n\times n},\bar{g}_{i} \in \mathbb{R}^{n}(i=1\cdots d),\bar{\sigma}_{p}^2$はハイパーパラメータです。${\rm I}_{n}$は$n$次元の単位行列です。
なお、重み係数$(\theta_{i,a})_{i=1\cdots d,a=1\cdots A}$は以下を満たします。
$$
\sum_{i=1\cdots d}\theta_{i,a} = 1, 0 \leq \theta_{i,a} \leq 1, a \in {1\cdots A}, i \in { 1\cdots d}.
$$
次時刻の状態の期待値は次の通りです。
$$
{\cal E}[s'|s,a] = F_{a} s + g_{a}, \
F_{a} = \sum_{i=1\cdots d} \theta_{i,a} F_{i},
g_{a} = \sum_{i=1\cdots d} \theta_{i,a} g_{i},
a \in 1\cdots A.
$$
次時刻の状態の期待値は、行動に応じて決まる重み係数$F_{a}$と定数係数$g_{a}$を持つ、現時刻の状態の線形関数に従います。前回の試みでは、$F_{a} = {\rm I}_{n}$と制限していました[2]。今回のモデルでは、表現できる状態遷移のクラスを、線形時不変システムを含むクラスまで拡げたことになります。
状態価値関数および行動価値関数のモデル
状態価値関数および行動価値関数をガウス過程回帰を使ってデータから推定しました。
状態価値関数の近似関数は以下の通りです。
$$
v(s) = \sum_{j = 1\cdots N} v_{j} {\cal N}(s|\bar{s}_{j}, \sigma^2_{v}{\rm I}_{n}) + b_{v}.
$$
$v_{j}(j=1\cdots N),b_{v},\sigma^{2}_{v}$は未知パラメータであり、データから学習します。
行動価値関数の近似関数は以下の通りです。
$$
q(s,a) = \sum_{j = 1\cdots N} q_{j,a} {\cal N}(s|\bar{s}_{j}, \sigma^2_{q}{\rm I}_{n}) + b_{q,a}.
$$
$q_{j,a}(j=1\cdots N,a=1\cdots A),b_{q,a}(a=1\cdots A),\sigma^2_{q}$は未知パラメータであり、データから学習します。
なお、状態価値関数および行動価値関数にあらわれる$\bar{s}_{j}(j=1\cdots N)$は学習データです。
2.2. 学習データ
学習データについては前回の記事[2]と概ね同様です。
状態および行動の学習データを、それぞれ、$\bar{s}_{1}\cdots \bar{s}_{N+1}\in\mathbb{R}^{n}$、$\bar{a}_{1}\cdots \bar{a}_{N} \in {1\cdots A}$とします。なお、$N$はサンプル数です。数値実験では、一様分布に従う乱数で生成しました。
2.3. アルゴリズム
簡易版UCLKのアルゴリズムを説明します。学習データから未知パラメータを求めます。ハイパーパラメタの一覧は表2.1にまとめました。
- 未知パラメタを初期化します。
\begin{align*} b_{v} &= 0\\ v_{j} &= 0, ~ j = 1\cdots N\\ \sigma^2_{v} &= \bar{\sigma}^2_{p},\\ b_{q,a} &= 0, ~ a = 1\cdots A\\ q_{j,a} &= 0, ~ j = 1\cdots N, a = 1\cdots A \\ \theta_{i,a} &= \frac{1}{d}, ~ i = 1\cdots d, a = 1\cdots A. \end{align*} - $a = 1\cdots A$ それぞれについて、$(Q_{t,a})_{t = 1 \cdots N, a = 1\cdots A}, (X_{t,j})_{t = 1 \cdots N,j = 1\cdots N}$ を以下のように計算します。第一式の第二項の積分は解析的に計算できます。なお、UCLKと同様に[1]、報酬関数$r(s,a)$を既知と仮定します。
\begin{align*} Q_{t,a} &= r(\bar{s}_{t}, a) + \gamma \int {\rm d}s' p(s'|\bar{s}_{t},a) v(s'), \\ X_{t,j} &= {\cal N}(\bar{s}_{t}|\bar{s}_{j}, \sigma_{q}^2 {\rm I}_{n}). \end{align*} - $a = 1\cdots A$ それぞれについて、説明変数を$(X_{t,j})_{t=1\cdots N, j = 1\cdots N}$、目的変数を$(Q_{t,a})_{t=1\cdots N}$として、ガウス過程回帰によって重み係数、バイアスおよび基底関数のスケールを求めて、$(q_{j,a})_{j=1\cdots N},b_{q,a},\sigma_{q}^2$とします。
- $(V_{t})_{t=1\cdots N}$および$(X_{t,j})_{t = 1 \cdots N,j = 1\cdots N}$を以下のように計算します。
\begin{align*} V_{t} &= \max_{a=1\cdots A} q(\bar{s}_{t}, a),\\ X_{t,j} &= {\cal N}(\bar{s}_{t}|\bar{s}_{j}, \sigma_{v}^2 {\rm I}_{n}). \end{align*} - 説明変数を$(X_{t,j})_{t=1\cdots N, j = 1\cdots N}$、目的変数を$(V_{t})_{t=1\cdots N}$として、ガウス過程回帰によって重み係数、バイアスおよび基底関数のスケールを求めて、$(v_{j})_{j=1\cdots N},b_{v},\sigma_{v}^2$とします。
- 手順2-5 を
n_round回繰り返します。 - $a=1\cdots A$ それぞれについて、手順8,9,10を実行します。
- 行動の学習データが$a$に一致するサンプル時点を$t_{1},\cdots,t_{N'}$とする。
\bar{a}_{t_{1}} = \bar{a}_{t_{2}} = \cdots = \bar{a}_{t_{N'}} = a - $(Y_{t}, X_{t,j})_{t = t_{1}\cdots t_{N'}, j = 1\cdots d}$を以下の通り計算します。
\begin{align*} X_{t,j} &= \int {\rm d}s' {\cal N}(s'|\bar{F}_{j}\bar{s}_{t} + \bar{g}_{j},a)v(s'),\\\\ Y_{t} &= v(\bar{s}_{t+1}). \end{align*} - 説明変数を$(X_{t,j})_{t = t_{1}\cdots t_{N'}, j = 1\cdots d}$、目的変数を$(Y_{t})_{t = t_{1}\cdots t_{N'}}$として、以下の最適化問題を解くことで重み係数を求めて、$(\theta_{i,a})_{i=1\cdots d}$とします。なお、制約条件の第一式は、回帰計算によって求めた重み係数でもって混合した結合ガウスモデルが確率密度分布になるための必要条件から導きました。
\begin{align*} {\rm minimize} & \sum_{t=t_{1}\cdots t_{N'}} (Y_{t} - \sum_{j=1\cdots d} X_{t,j} \theta_{j,a})^2\\ {\rm subject~to} &\sum_{j=1\cdots d} \theta_{j,a} = 1,\\ & 0 \leq \theta_{j,a} \leq 1, ~ j = 1\cdots d. \end{align*} - 手順2-10を
n_itr回反復します。
表2.1. ハイパーパラメータの一覧
| パラメタの名称 | 説明 |
|---|---|
n_round |
手順2-5の反復回数 |
n_itr |
手順2-10の反復回数 |
| $\gamma$ | 割引率 |
| $d$ | 特徴ベクトルの次元 |
| $\bar{\sigma}_{p}^2$ | 遷移関数のパラメタ(2.1節参照) |
| $\bar{F}_{i}(i=1\cdots d)$ | 遷移関数のパラメタ(2.1節参照) |
| $\bar{g}_{i}(i=1\cdots d)$ | 遷移関数のパラメタ(2.1節参照) |
3. 数値実験
3.1. 制御対象
制御対象は、ばねマスダンパ系で、こちらの記事を参考にしました。
状態方程式は以下の通りです。
$$
\begin{align*}
\dfrac{{\rm d}x}{{\rm d}t} &= v,\\
m\dfrac{{\rm d}v}{{\rm d}t} &= -kx -cv + f.
\end{align*}
$$
なお、$x,v$は、それぞれ、おもりの位置および速度です。状態変数$s$は2次元のベクトルで$s = (x,v)^{\rm T}\in\mathbb{R}^2$です。$m,c,k$は、それぞれ、おもりの質量、減衰係数、ばね係数で、$1,1,10$としました。$f$は外力です。行動は、有限個の集合${0,1}$の要素とします。行動$a$が0あるいは1のとき、外力$f$を以下の通り設定します。
$$
\begin{align*}
f &= -3 &~ (a = 0)\\
f &= 3 &~ (a = 1)
\end{align*}
$$
すなわち、$a=0$では負の方向に加速するように外力をかけて、$a=1$では正の方向に外力をかけます。
制御の目標は、任意の初期状態から原点$x=0$に収束させることです。このため、報酬は次のように設定しました。
$$
\begin{align*}
r(x,v,a) = -|x|
\end{align*}
$$
すなわち、速度$v$および行動$a$に関わらず、位置の原点からの偏差をペナルティとしています。
なお、制御対象は、前回の記事[2]から変更していません。
3.2. ハイパーパラメータ
ハイパーパラメータは表3.1に示す値に設定しました。
表3.1. ハイパーパラメタの設定値
| パラメタの名称 | 説明 | 設定値 |
|---|---|---|
n_round |
手順2-5の反復回数 | 1 |
n_itr |
手順2-10の反復回数 | 16 |
| $\gamma$ | 割引率 | 0.9 |
| $d$ | 特徴ベクトルの次元 | 128 |
| $\bar{\sigma}_{p}$ | 基底関数の分散 | 0.4 |
| $\bar{F}_{i}(i=1\cdots d)\in\mathbb{R}^{2\times 2}$ | 遷移関数のパラメタ | 平均0、分散$1/3$の正規分布からサンプルした |
| $\bar{g}_{i}(i=1\cdots d)\in\mathbb{R}^{2}$ | 遷移関数のパラメタ | 平均0、分散$1/3$の正規分布からサンプルした |
| $N$ | 学習データのサンプル数 | 128 |
3.3. 実験結果
数値実験の結果を説明します。
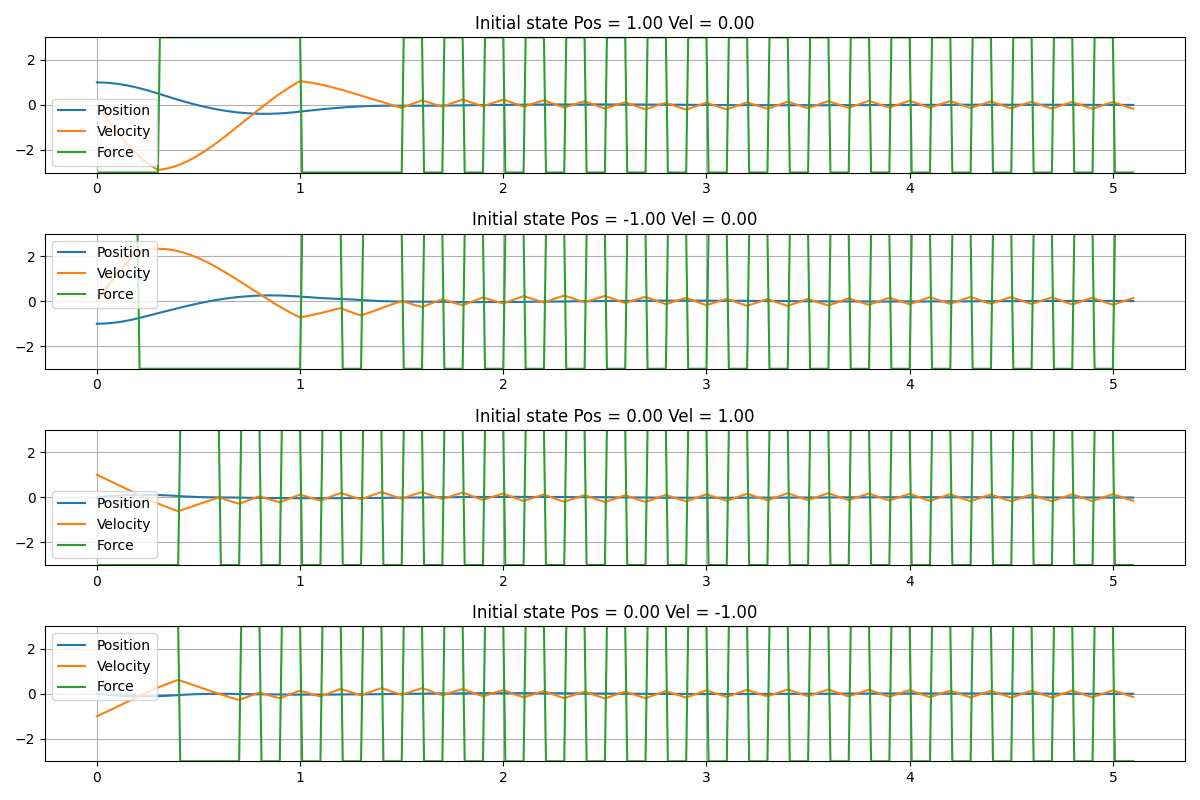
結果1: 学習した方策による制御シミュレーション
簡易版UCLKのアルゴリズムに従って学習した方策を使って、ばねマスダンパ系のシミュレータを制御した結果を紹介します。図3.1は、シミュレーションの結果です。4種類のシミュレーションをした結果を図に掲載しました。上から順番におもりの初期状態を以下の通り設定しました。
- 位置 = 1、速度 = 0
- 位置 = -1、速度 = 0
- 位置 = 0、速度 = 1
- 位置 = 0、速度 = -1
図3.1に掲載した4つのシミュレーション結果のうち、1番初めの結果を見ると、初期時刻ではおもりが正の位置にあるため、おもりに負の方向の外力をかけています。また、時刻0.3付近で、速度が負の方向に加速し過ぎたため、おもりに正の方向に力をかけて引き戻しています。同様に、時刻1付近でも、正の方向に加速しすぎたため、おもりに負の方向の外力をかけて引き戻しています。十分時間が経過した後には、正の方向と負の方向、それぞれに、等しい頻度で外力がかかっていて、おもりは原点付近で小さな振動をしています。この数値実験では、外力を$f=3$および$f=-3$のいずれか一方から選択するように操作量を決めています。この制約があるため、同じ頻度で力を加えることで、外力を加えない状態を作り出し、おもりを原点付近に保っています。
図3.1. 学習した方策で制御対象を制御したシミュレーションの結果
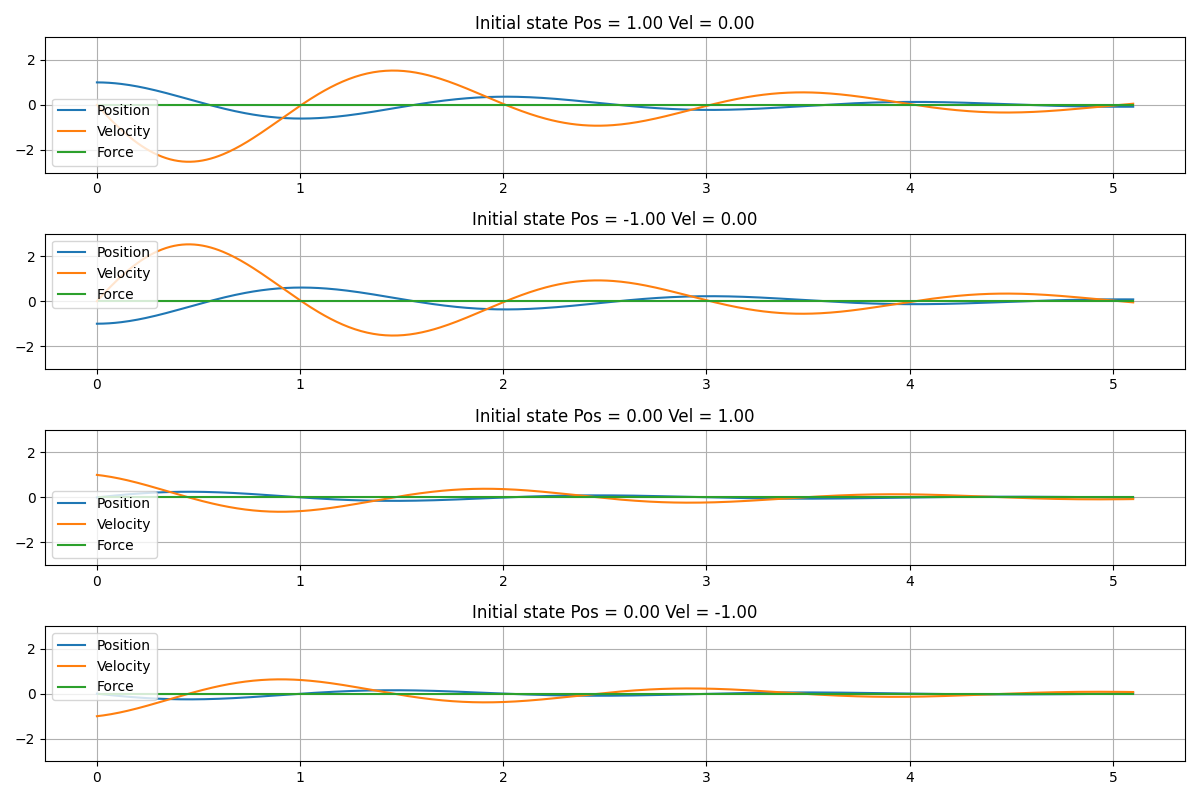
図3.2は、外力をかけずに$(f=0)$、おもりを自由に振動させた場合のシミュレーション結果です。図3.1と図3.2を比較すると、学習した方策で制御することによって、速やかにおもりの速度が0に収束していることが見て取れます。
図3.2. 外力$f=0$として、おもりを自由振動させたシミュレーションの結果
結果2: 学習した行動価値関数の特徴
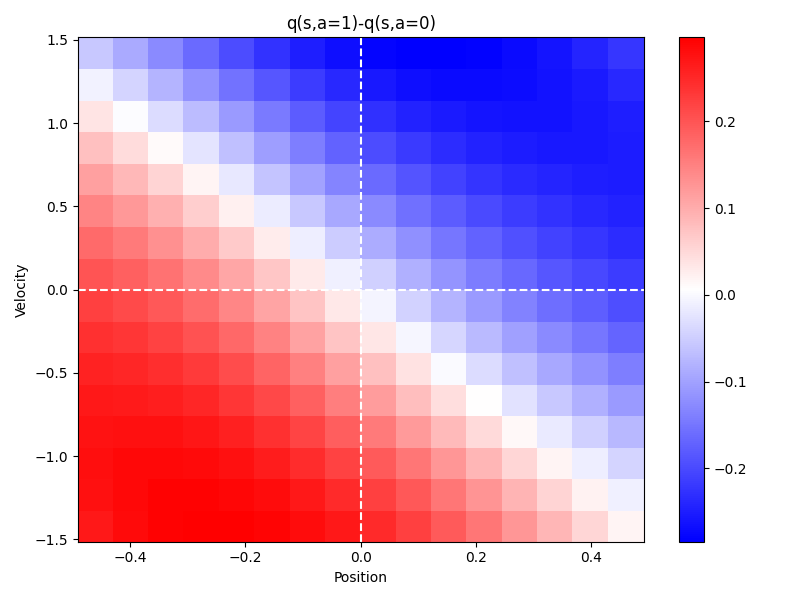
行動価値関数の推定結果を説明します。
図3.3に行動価値関数の推定結果を示しました。おもりの状態(位置と速度の組合せ)ごとに、正の方向に外力を加えた場合の価値関数$q(s,a=1)$から、負の方向に外力を加えた場合の価値関数$q(s,a=0)$を差し引いた値を色分けして示しています。
- 例えば、チャートの第一象限では、大部分の領域で青く着色されていて、負の方向に外力を加えた方が、正の方向に外力を加えるよりも価値関数が大きいこと表します。おもりが正の位置にあって、かつ正の速度で運動する場合に、負の方向に力を加えているので、期待通りの制御ができます。
- また、チャートの第四象限では、おもりが正の位置にあって、負の方向にゆっくり運動する領域では、青く着色されているため、負の方向に力を加える方が、正の方向に外力を加えるよりも価値関数が大きいこと表します。一方、負の方向に十分早く運動する領域では、赤く着色されているため、正の方向に外力を加える方が、価値関数が大きいことを表します。おもりが正の位置にあって、負の速度で運動する場合には、速度に応じて、外力の向きを調整しているので、やはり期待通りの制御動作となっています。
以上のように、位置あるいは速度について偏差がある場合に原点に引き戻すように力がかかるため、結果1で示したように原点に収束するように制御することができた、と考えられます。
図3.3. 行動価値関数の推定結果
おもりの位置および速度の組合せごとに、正の外力を加えた場合の価値関数$q(s,a=1)$から負の外力を加えた場合の価値関数$q(s,a=0)$を差し引いた値を色分けした
結果3: 学習した遷移関数による状態遷移の予測結果
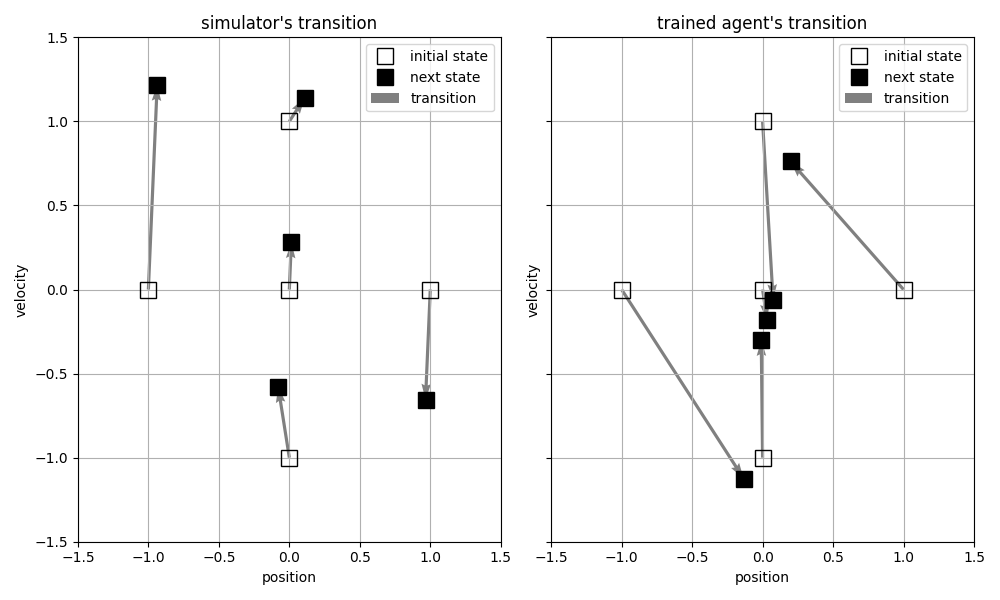
学習した遷移関数により次時刻の状態を予測した結果を説明します。
図3.4に、ばねマスダンパ系のシミュレータにより算出した次時刻におけるおもりの位置および速度と、学習した遷移関数により予測した結果をそれぞれ示しました。おもりの位置と速度の初期状態を、原点(0,0)、(1,0)、 ... などと設定して、正の外力を加えた場合の状態遷移を、合計5種類のパターンで示しています。
学習した遷移関数による状態遷移の予測結果(右図)は、ばねマスダンパ系のシミュレータによる状態遷移(左図)とまったく一致していません。特に、正の外力を加えたときに、正の方向に速度が加速する、という定性的な性質すら成立していません。
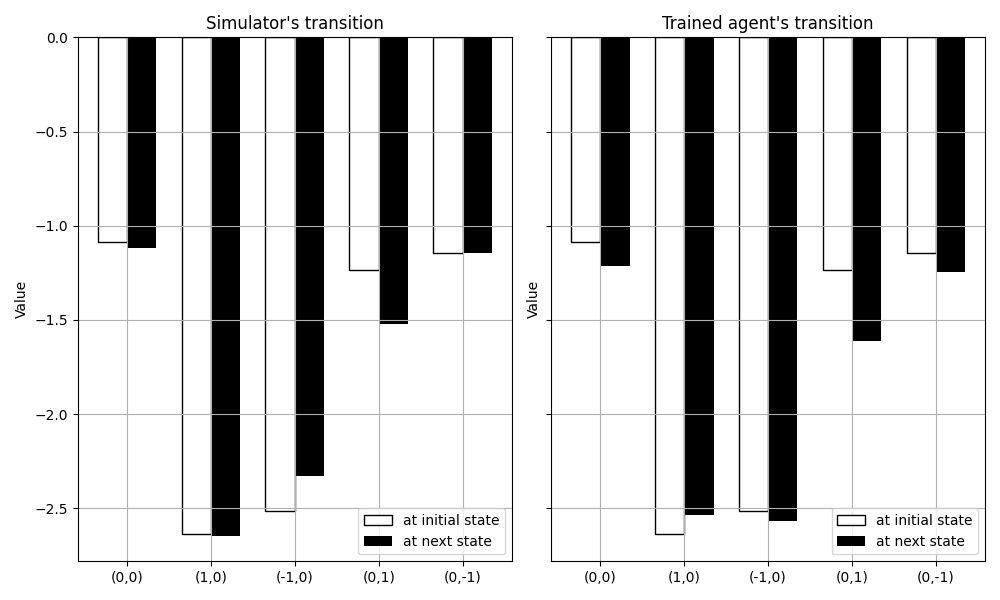
図3.5に、状態遷移前後の価値関数の推定値を示します。左図には、初期状態およびシミュレータにより算出した次時刻の状態、それぞれにおける状態価値関数の推定値を示しました。学習した遷移関数について、同様の図を右図に示しました。次時刻における状態価値関数の推定値(左図および右図の黒のバーの高さ)は、シミュレータと学習した遷移関数の間で概ね一致します。
UCLKは、状態遷移関数を学習するときに、状態(おもりの位置と速度)の予測誤差ではなく、状態価値関数の予測誤差を小さくするように学習します。状態(おもりの位置と速度)の違いが状態価値関数にそれほど影響しない場合には、予測誤差を小さくするように状態遷移関数のパラメタを学習しません。このため、状態の違いが価値関数にそれほど影響しないことから、学習した遷移関数とばねマスダンパ系のシミュレータで状態遷移が異なった、と考えられます。
また、結果1に示したように、簡易版UCLKで設計したコントローラで、ばねマスダンパ系のシミュレータを期待通りに制御できています。状態(おもりの位置と速度)を正しく予測することは、必ずしも必要ではないのかもしれません。
図3.4. シミュレータおよび学習した遷移関数で算出した状態遷移
おもりの初期状態(位置と速度の組合せ)を、それぞれ、(0,0),(1,0),(0,1),(-1,0),(0,-1)として、正の外力を加えた場合の状態遷移
左図: ばねマスダンパ系のシミュレータによる次状態の算出結果, 右図: 学習した遷移関数による次状態の予測結果
図3.5. 状態遷移前後の状態価値関数の推定値
おもりの初期状態(位置と速度の組合せ)を、それぞれ、(0,0),(1,0),(0,1),(-1,0),(0,-1)として、正の外力を加えた場合の状態遷移
左図: ばねマスダンパ系のシミュレータによる次状態の算出結果, 右図: 学習した遷移関数による次状態の予測結果
3.4 ソースコード
ソースコードはこちらに公開しました。
4. 終わりに
この記事では、記事[2]で紹介した簡易版UCLKを改造して、モデルで表現できる動特性のクラスを線形システムまで拡張する工夫を紹介しました。ばねマスダンパ系を制御対象にした数値実験では、簡易版UCLKで学習したコントローラにより、偏差なく制御できること、行動価値関数が期待通りに学習できたことを示しました。また、学習したモデルによって次時刻におけるおもりの位置および速度を予測した結果は真値から外れることを示しました。さらに、おもりの位置および速度の予測が不正確であるにも関わらず、状態価値関数の予測値はおおむね正しいことを示しました。
興味を持っていただいたら、幸いです。
参考文献
- [1]: Zhou, D., He, J., & Gu, Q. (2020). Provably Efficient Reinforcement Learning for Discounted MDPs with Feature Mapping. International Conference on Machine Learning.
- [2]: カーネル法を使った強化学習のアルゴリズムの数値実験による検証