1. はじめに
文献[1]で、UCLK(Upper-Confidence Linear Kernel reinforcement learning)という強化学習のアルゴリズムが提案されました。このアルゴリズムには、次のような特徴があります。
- (1) 状態および行動を特徴量に変換すること
- (2) 制御対象の動特性が特徴量の線形和に従う、と仮定すること、
- (3) また、それぞれの特徴量の重み係数をオンラインで学習すること
- (4) 学習した動特性のモデルに基づいて、状態価値関数および行動価値関数を求めること
- (5) 動特性のパラメタは、観測出力の予測誤差ではなくて、状態価値関数の予測誤差に基づいて学習すること
最近提案された強化学習のアルゴリズムは、多くの場合、ニューラルネットワークを使って価値関数や方策を実装するため、コーディングにも学習の計算にも苦労していました。基底関数を使うことで、アルゴリズムの実装や応用が軽快になることを期待しています。
この記事では、文献[1]で提案されたUCLKを以下のように簡略化したアルゴリズム(以下、簡易版UCLK)を実装し、効果を検証した結果を報告します。
- オンラインでデータ収集しながらパラメタを学習する代わりに、オフラインで収集したデータを使ってパラメタを学習しました。
- UCLKでは探索過程でデータの多様性を保つために、価値関数を正則化します。今回は、正則化をつけませんでした。
- UCLKでは状態遷移関数を基底関数で近似します。ここでは、遷移関数に加えて、状態および行動価値関数もそれぞれ基底関数で近似しました。
(2023/03/05 追記)遷移関数のパラメタを算出するアルゴリズムを修正しました。修正にともなって、アルゴリズムの解説、結果、考察を修正しました。
2. アルゴリズム
状態を1次元の実数に限定してアルゴリズムを説明します。任意の次元に拡張することができます。
未知パラメータ
状態の遷移関数は次のように定義されます。
$$
p(s'|s,a) = \sum_{i=1\cdots d} \theta_{i,a} \phi_{i}(s'-s)
$$
$s'\in\mathbb{R},s\in\mathbb{R},a\in {1\cdots A}$は、それぞれ、次時刻の状態、現時刻の状態、現時刻の行動です。$A$は、取りうる行動の数です。$\phi_{i}(i=1\cdots d)$は基底関数で、中心$\bar{s}_{i}$、分散$\bar{\sigma}^2$のガウス関数とします。$d$は特徴ベクトルの次元です。$(\theta_{i,a})_{i=1\cdots d, a=1\cdots A}$ は動特性の重み係数です。$(\theta_{i,a})_{i=1\cdots d, a=1\cdots A}$は、以下を満たすとします。
$$
\sum_{i=1\cdots d} \theta_{i,a} = 1, ~ a \in {1\cdots A}
$$
$(v_{j})_{j=1\cdots}$は状態価値関数の重み係数で、$b^{v}$はバイアスです。状態価値関数は次のように近似されます。
$$
v(s) = \sum_{j=1\cdots d} v_{j} \phi_{j}(s) + b^{v}
$$
$(q_{j,a})_{j=1\cdots,a=1\cdots A}$は行動価値関数の重み係数で、$(b^{q}_{a})_{a=1\cdots A}$はバイアスです。行動価値関数は次のように近似されます。
$$
q(s,a) = \sum_{j=1\cdots d} q_{j,a} \phi_{j}(s) + b^{q}_{a}
$$
学習データ
状態および行動の学習データを、それぞれ、$s_{1}\cdots s_{N+1}\in\mathbb{R}$、$a_{1}\cdots a_{N} \in {1\cdots A}$とします。なお、$N$はサンプル数です。数値実験では、一様分布に従う乱数で生成しました。
アルゴリズム
簡易版UCLKのアルゴリズムを説明します。学習データから未知パラメータを求めます。ハイパーパラメタの一覧は表2.1にまとめました。
- 未知パラメタを初期化します。
\begin{align*} b^{v} &= 0\\ v_{j} &= 0, ~ j = 1\cdots d\\ b_{a}^{q} &= 0, ~ a = 1\cdots A\\ q_{j,a} &= 0, ~ j = 1\cdots d, a = 1\cdots A \\ \theta_{i,a} &= \frac{1}{d}, ~ i = 1\cdots d, a = 1\cdots A. \end{align*} - $a = 1\cdots A$ それぞれについて、$(Q_{t,a})_{t = 1 \cdots N, a = 1\cdots A}, (X_{t,j})_{t = 1 \cdots N,j = 1\cdots d}$ を以下のように計算します。第一式の第二項の積分は解析的に計算できます。なお、UCLKでは、報酬関数$r(s,a)$を既知としています。
\begin{align*} Q_{t,a} &= r(s_{t}, a) + \gamma \int {\rm d}s' p(s'|s_{t},a) v(s'), \\ X_{t,j} &= \phi_{j}(s_{t}). \end{align*} - $a = 1\cdots A$ それぞれについて、説明変数を$X_{t,j}$、目的変数を$Q_{t,a}$として、リッジ回帰によって重み係数とバイアスを求めて、$(q_{j,a})_{j=1\cdots d},b_{a}^{q}$とします。
- $(V_{t})_{t=1\cdots N}$を以下のように計算します。
V_{t} = \max_{a=1\cdots A} \left( \sum_{j=1\cdots d} \phi_{j}(s_{t}) q_{j,a} \right) - 説明変数を$X_{t,j}$、目的変数を$V_{t}$として、リッジ回帰によって重み係数とバイアスを求めて、$(v_{j})_{j=1\cdots d},b^{v}$とします。
- 手順2-5 を
n_round回繰り返します。 - $a=1\cdots A$ それぞれについて、手順8,9,10を実行します。
- 行動の学習データが$a$に一致するサンプル時点を$t_{1},\cdots,t_{N'}$とする。
a_{t_{1}} = a_{t_{2}} = \cdots = a_{t_{N'}} = a - $(Y_{t}, X_{t,j})_{t = t_{1}\cdots t_{N'}, j = 1\cdots d}$を以下の通り計算します。
\begin{align*} X_{t,j} &= \int {\rm d}s' \phi_{j}(s'-s_{t})v(s'),\\\\ Y_{t} &= v(s_{t+1}). \end{align*} - (2023/03/05修正)
説明変数を$X_{t,j}$、目的変数を$Y_{t}$として、リッジ回帰によって重み係数を求めて、$(\theta_{i,a})_{i=1\cdots d}$とします。説明変数を$(X_{t,j})_{t = t_{1}\cdots t_{N'}, j = 1\cdots d}$、目的変数を$(Y_{t})_{t = t_{1}\cdots t_{N'}}$として、以下の最適化問題を解くことで重み係数を求めて、$(\theta_{i,a})_{i=1\cdots d}$とします。なお、制約条件の第一式は、回帰計算によって求めた重み係数でもって混合した結合ガウスモデルが確率密度分布になるための必要条件から導きました。
\begin{align*}
{\rm minimize} & \sum_{t=t_{1}\cdots t_{N'}} (Y_{t} - \sum_{j=1\cdots d} X_{t,j} ,\theta_{j,a})^2\\
{\rm subject~to} &\sum_{j=1\cdots d} \theta_{j,a} = 1,\\
& 0 \leq \theta_{j,a} \leq 1, ~ j = 1\cdots d.
\end{align*}
- 手順2-10を
n_itr回反復します。
表2.1. ハイパーパラメータの一覧
| パラメタの名称 | 説明 |
|---|---|
n_round |
手順2-5の反復回数 |
n_itr |
手順2-10の反復回数 |
| $d$ | 特徴ベクトルの次元 |
| $(\bar{s}_{j})_{j=1\cdots d}$ | 基底関数の中心 |
| $\bar{\sigma}^2$ | 基底関数の分散 |
3. 数値実験
簡易版UCLK を数値実験で検証しました。
3.1. 制御対象
制御対象は、ばねマスダンパ系で、こちらの記事を参考にしました。
状態方程式は以下の通りです。
$$
\begin{align*}
\dfrac{{\rm d}x}{{\rm d}t} &= v,\\
m\dfrac{{\rm d}v}{{\rm d}t} &= -kx -cv + f.
\end{align*}
$$
なお、$x,v$は、それぞれ、おもりの位置および速度です。状態変数$s$は2次元のベクトルで$s = (x,v)^{\rm T}\in\mathbb{R}^2$です。$m,c,k$は、それぞれ、おもりの質量、減衰係数、ばね係数で、$1,1,10$としました。$f$は外力です。行動は、有限個の集合${0,1}$の要素とします。行動が$a\in{0,1}$のとき、外力$f$を以下の通り設定します。
$$
\begin{align*}
f &= -3 &~ (a = 0)\\
f &= 3 &~ (a = 1)
\end{align*}
$$
すなわち、$a=0$では負の方向に加速するように外力をかけて、$a=1$では正の方向に外力をかけます。
制御の目標は、任意の初期状態から原点$x=0$に収束させることです。
3.2. 状態の遷移関数の性質
簡易版UCLKでは、状態の遷移関数を次のように設計しました。
$$
p(s'|s,a) = \sum_{i=1\cdots d} \theta_{i,a} \phi_{i}(s'-s).
$$
現時刻の状態$s = (x,v)^{\rm T}$、次時刻の状態$s'=(x',v')^{\rm T}$とすると、次時刻の状態の確率密度関数は次の式に従います。
$$
p(x',v'|x,v,a) = \sum_{i=1\cdots d} \theta_{i,a}
{\cal N}(x';x+\bar{x}_{i},\bar{\sigma}^2){\cal N}(v';v+\bar{v}_{i},\bar{\sigma}^2)
$$
特に、次時刻の状態の期待値は、
\begin{align*}
{\cal E}[x'|x,v,a] &= x + \sum_{i=1\cdots d} \theta_{i,a} \bar{x}_{i},~\\
{\cal E}[v'|x,v,a] &= v + \sum_{i=1\cdots d} \theta_{i,a} \bar{v}_{i},
\end{align*}
となっていて、現時刻の状態に、操作によって決まる一定のシフト幅を加えたものなっています。
ばねマスダンパ系の位置に関する動特性は速度に依存することから、このモデルは、制御対象の状態方程式と構造的に一致していません。この条件の下で、どういった制御ができるか、またどんな問題があるか検証します。
3.3. 実験結果
数値実験の結果を説明します。なお、ハイパーパラメータは表3.1に示す値に設定しました。
表3.1. ハイパーパラメタの設定値
| パラメタの名称 | 説明 | 設定値 |
|---|---|---|
n_round |
手順2-5の反復回数 | 2 |
n_itr |
手順2-10の反復回数 | 2 |
| $d$ | 特徴ベクトルの次元 | 32 |
| $(\bar{s}_{j})_{j=1\cdots d}$ | 基底関数の中心 | -3から3の間で一様分布する確率分布からサンプルした |
| $\bar{\sigma}^2$ | 基底関数の分散 | 1 |
| $N$ | 学習データのサンプル数 | 2048 |
結果1: 学習した方策による制御シミュレーション
簡易版UCLKのアルゴリズムに従って学習した方策を使って、制御対象のばねマスダンパ系を制御するシミュレーションをした結果を紹介します。
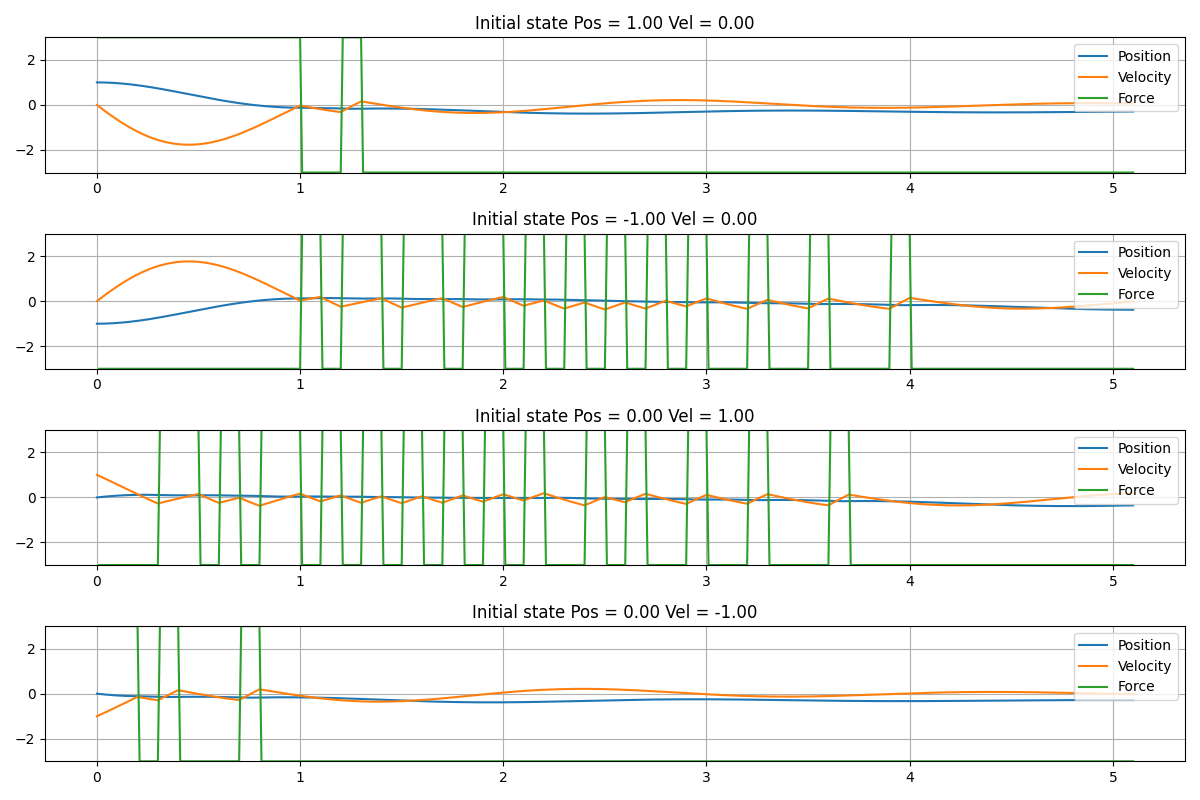
図3.1は、シミュレーションの結果です。4種類のシミュレーションをした結果を図に掲載しました。上から順番に初期条件を以下の通り設定しました。
- 位置 = 1 速度 = 0
- 位置 = -1 速度 = 0
- 位置 = 0 速度 = 1
- 位置 = 0 速度 = -1
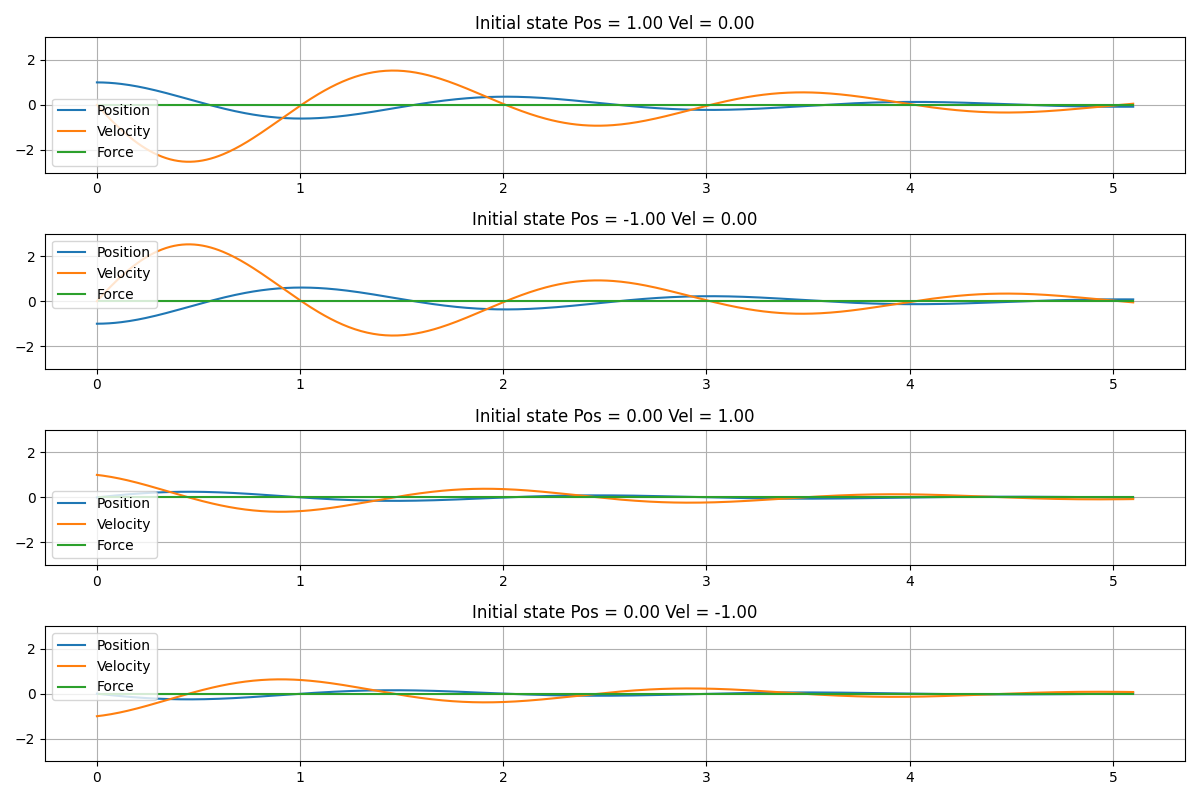
図3.2は、外力をかけずに$(f=0)$、おもりを自由に振動させた場合のシミュレーション結果です。
図3.1から、速度が正の場合に、おもりに負の力$f = -3$がかかり、速度が負の場合には、正の力$f = 3$がかかっていることが見て取れます。図3.1と図3.2を比較すると、学習した方策で制御することによって、速やかにおもりの速度が0に収束していることが見て取れます。また、初期時刻から十分時間が経過した後に、位置について定常偏差が残り、かつ、力が$f=-3$で収束しています。
図3.1. 学習した方策で制御対象を制御したシミュレーションの結果
図3.2. 外力$f=0$として、おもりを自由振動させたシミュレーションの結果
結果2: 行動価値関数の推定結果
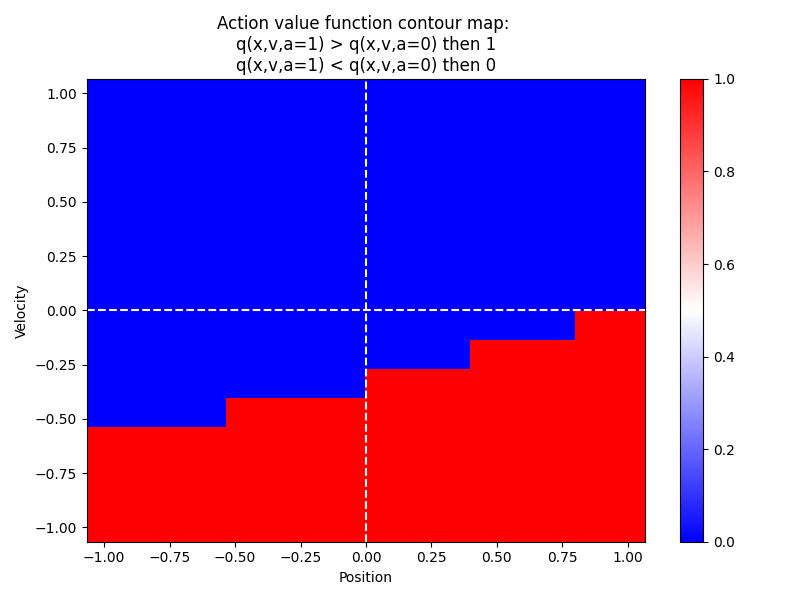
図3.3は、行動価値関数の推定結果です。
行動価値関数は位置$x$、速度$v$、行動$a$の関数$q(x,v,a)$です。また、行動は、この数値計算では、$a=0$、すなわち、負の外力を入れる場合と、$a=1$、すなわち、正の外力を入れる場合の2種類です。図3.3には、位置$x$、速度$v$それぞれにおいて、行動価値関数$q(x,v,a)$が、
- $q(x,v,a=0) < q(x,v,a=1)$ となる場合、すなわち、正の外力を加えた方が価値関数が大きくなる場合、赤
- $q(x,v,a=0) > q(x,v,a=1)$ となる場合、すなわち、負の外力を加えた方が価値関数が大きくなる場合、青、
と色分けしました。
速度$v$が正の場合には、負の外力を加えた方が、価値関数が大きくなっています。逆に、速度$v$が負の場合には、正の外力を加えた方が、価値関数が大きくなっています。つまり、おもりが動いているときには、その動きを止める方向に力が働いています。
一方、位置が正のときに、正の外力を加える方が、価値関数が大きくなっています。また、位置が負のときに、負の外力を加える方が、価値関数が大きくなっています。おもりが基準の位置からずれていても、偏差を小さくする方向に力がかからないことを表します。
フィードバックシミュレーションの結果で、速度については収束していたけれども、位置について定常偏差が残った、という結果と辻褄があいます。
図3.3 行動価値関数の推定結果
(赤: 正の外力を加えた方が価値関数が大きくなる領域、青: 負の外力を加えた方が価値関数が大きくなる領域)
結果3: 遷移関数の推定結果
学習した遷移関数によって位置および速度を予測した結果と、制御対象のばねマスダンパ系の応答を比較します。
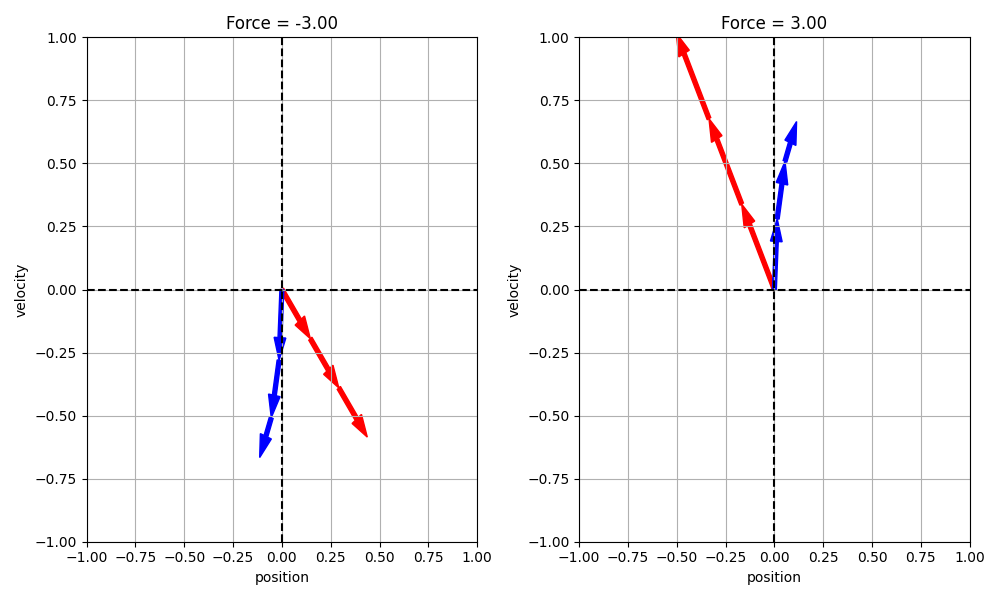
図3.4には、初期時刻で位置$x=0$、速度$v=0$であるおもりを、3ステップ先までシミュレーションした結果を掲載しています。図3.4の左図は、負の外力を加えてシミュレーションした結果で、右図は正の外力を加えた結果です。赤の矢印が、学習した遷移関数により予測した結果で、青の矢印が、制御対象のばねマスダンパ系の応答を表します。
(2023/03/05 修正)正の外力、負の外力を与えた場合、ともに、予測の結果は、まったく一致しません。負の外力を与えた場合に、負の方向に速度が加速する、という性質は一致しています。しかし、変化の大きさは、大きく異なります。 正の外力を加えた場合(図3.4(右))、ばねマスダンパ系のシミュレーション結果(青)によると、おもりは正の方向に加速し、位置が正の方向にシフトします。学習した遷移関数の予測(赤)によると、おもりは正の方向に加速し、位置が負の方向にシフトします。すなわち、速度の変化については、シミュレーションと予測で一致するのですが、位置については一致しませんでした。負の外力を加えた場合(図3.4(左))についても、やはり同様に、矢印の向きは、速度について一致して、位置について逆向きとなりました。
図3.4. 3ステップ先までの軌跡
(赤: 学習した遷移関数による予測の結果、青: 制御対象のばねマスダンパ系をシミュレーションした結果)
結果4: 遷移関数の推定結果
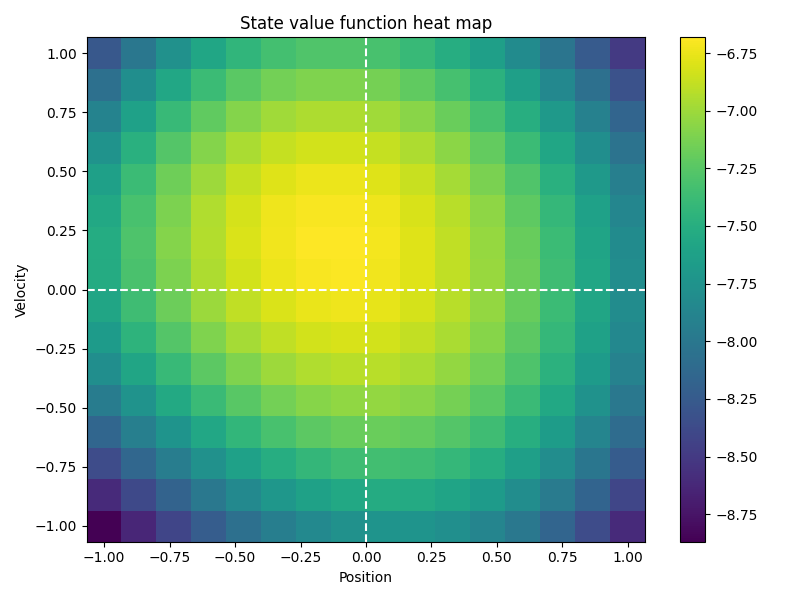
図3.5は、状態価値関数の推定結果です。状態価値関数は、位置$x$、速度$v$の関数です。状態価値関数$V(x,v)$は、ばねマスダンパ系を初期状態$(x,v)$から、学習した方策で制御したときのリターンを表します。
UCLKでは、状態価値関数の予測誤差を基準に遷移関数のパラメタを学習することから、状態価値関数がフラットの場合、2つの遷移関数が互いに異なっている場合でも、識別することができません。
図3.5において、状態価値関数の値は、それほど大きく変化していません。このことから、状態価値関数に影響を与えないために、遷移関数の推定が粗いものになった、と推測できます。
図3.5. 状態価値関数の推定結果
考察
(2023/03/05 修正)
位置変数の時間発展については、モデルの構造が制御対象の構造と一致しないために、時間発展を予測するのは難しいだろうと思っていました。そのためにフィードバックシミュレーションで、位置について定常偏差が残るのだろうと思っていました。しかし、図3.4の右図を見ると、位置変数どころか速度変数についても予測の方向も大きさもあっていません。それにも関わらず、フィードバックシミュレーションで速度は0に収束しています。この疑問は、まだ解消できていません。今後の検討課題とします。
モデルの構造が制御対象の構造と一致しないために、時間発展にともなう状態変数の変化の向きを予測できないだろう、と仮説を立てていました。すなわち、ばねマスダンパ系の位置変数の時間変化は、本来、速度に依存するのですが、遷移関数では、操作によって決まる一定の速度で平行移動するという動特性となっているため、位置変数の変化を予測できない、と想定していました。図3.4の予測結果は、この仮説を裏付けています。
行動価値関数は遷移関数に基づいて推定します。図3.3で、位置変数に偏差があるときに外力を加える利得を行動価値関数が推定できなかったのは、遷移関数が位置変数を予測できなかったため、と考えられます。
以上から、遷移関数と制御対象とで動特性の構造が一致しないために、図3.1のように、位置変数の定常偏差に対して制御がかからなかった、と考えることができます。
今回の遷移関数では、次状態の確率密度関数を、現在の状態を一定幅だけシフトした中心を持つガウス関数の結合分布で表現しました。制御性能を改善するには、もっと広いクラスの動特性を表現できるように遷移関数を定義を工夫する必要がありそうです。
3.4. ソースコード
数値実験に使ったソースコードはこちらに公開しております。
(2023/03/05 追記)遷移関数のパラメタを求めるアルゴリズムの修正にともなって、ソースコードも修正しました。
お気づきの点があれば、ご指摘ください。
参考文献
- [1]: Zhou, D., He, J., & Gu, Q. (2020). Provably Efficient Reinforcement Learning for Discounted MDPs with Feature Mapping. International Conference on Machine Learning.