LoginSignup
78
58

More than 3 years have passed since last update.

@arakiii(Hiroshi ARAKI)

Spiking Neural Networkとは何なのか

Last updated at Posted at 2019-12-13

はじめに

近年，深層学習における畳み込みニューラルネットワークをはじめとする機械学習が主流です．このニューラルネットワークとは，その名の通り生物の脳における神経回路網を模したものであり，それを構成する神経細胞を形式ニューロンとしてモデリングしたものがはじまりです．

しかし，この形式ニューロンは神経細胞の簡単なモデルに過ぎません．一部の研究者はより精緻なニューロンモデルを研究し，今日まで様々なニューロンモデルを提案してきました．

このような本来の神経細胞に，より近づけたニューロンモデルを一般的にスパイキングニューロンモデル (Spiking Neuron Models)と言います．またそれを用いたニューラルネットワークをスパイキングニューラルネットワーク (SNN: Spiking Neural Networks)と言います．

ここで「スパイク (Spike)」という単語が出てきましたが，このワードを理解するためには神経細胞の働きについてある程度詳しく知る必要があります．

ちなみに”詳しい話はどうでもいいから，どんなもんか早く見せてよ！”という方は「有名なモデル(Diehl＆Cook)を見てみる」に飛んでください．

神経細胞のはたらき

神経細胞は「入力を受け取り，それを処理して出力する」というとてもシンプルな作業を行なっています．
この説明だけだと訳がわからないので詳しく説明していきますが，その前にいくつかの前提知識が必要です．

- 膜電位とは何か

神経細胞は細胞の内側と外側で，多く存在するイオンが異なります．外側ではナトリウムイオン，内側ではカリウムイオンが多く存在しています．
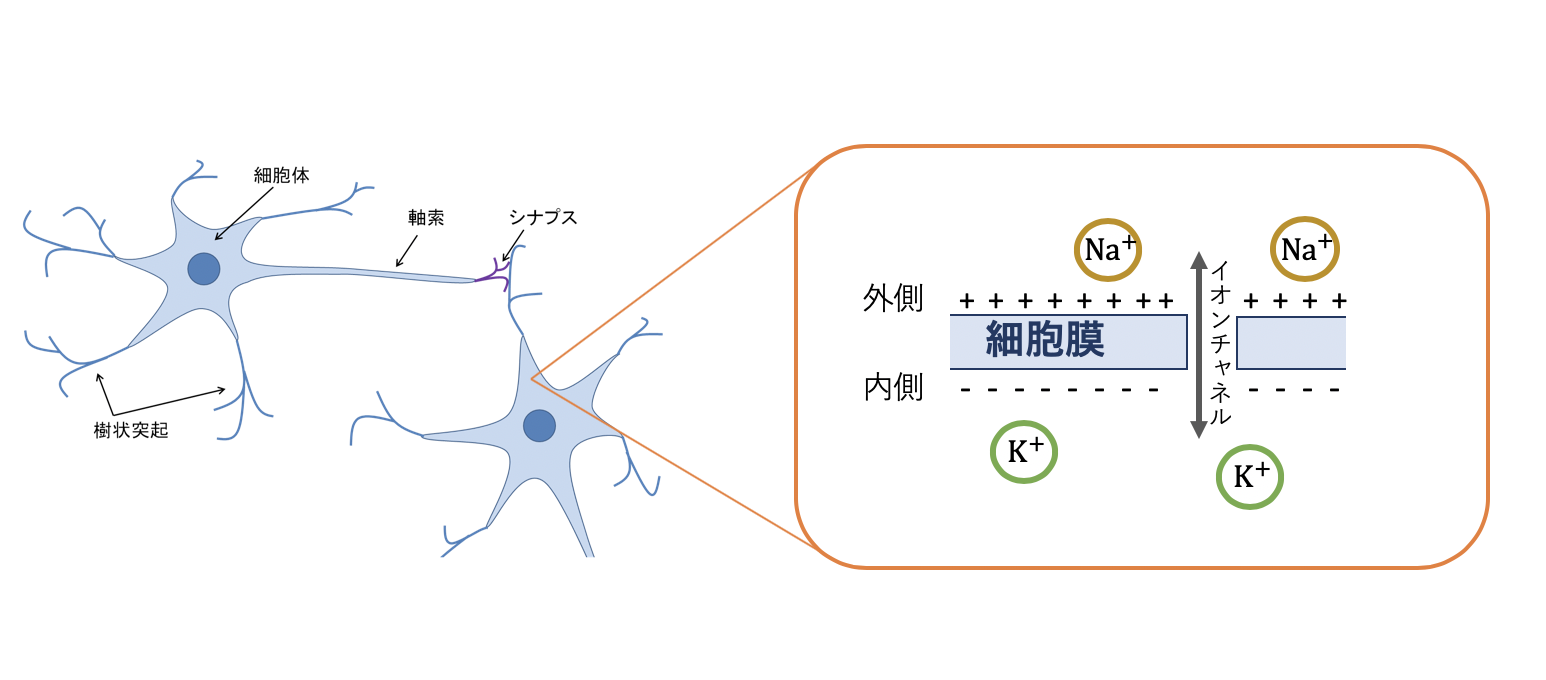
neuron

そのため細胞膜の内外では電位差があり，この電位差は膜電位 (Membrane Potential, Membrane Voltage)と呼ばれています．この膜電位は通常-65mV程度で安定しており，これを静止膜電位(Resting Potential)と言います．

- 膜電位とスパイク

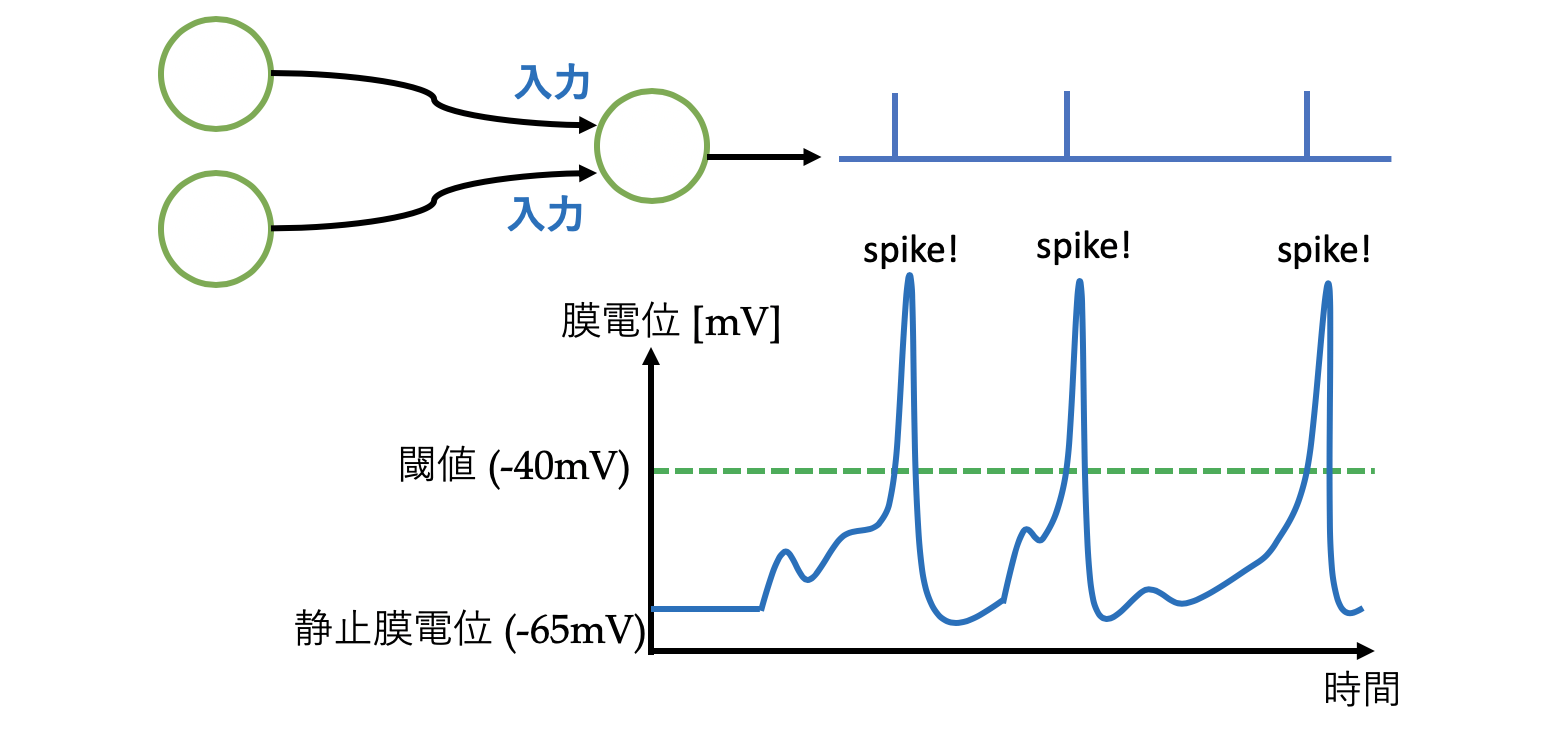
ここであるニューロンに，外部から刺激(入力)が入ったとき，膜電位は上昇しますが，時間と共に減衰し，また静止膜電位に落ち着きます．しかし，多くの刺激があると膜電位は上昇し続け，あるところに達すると膜電位は急上昇し，3msほどかけて静止膜電位に落ち着きます．

これを発火(fire)と言い，静止膜電位に落ち着くまでを不応期(Refractory period)と言います．
このとき，発火して膜電位が突出した部分をスパイクと言います．
membrane_voltage_and_spikes

- 神経細胞の情報

それでは，神経細胞の入出力(情報)はなんでしょうか？

形式ニューロンでは実数値が情報でしたので，膜電位の大きさと思うかもしれませんが，実際には「スパイクの発生時刻・頻度」が情報であると言われています．つまり，私たちの脳では，{0,1}のデジタル信号でやりとりが行われているのです．膜電位の大きさは関係ありません，重要なのはスパイクの有無です．

これを，悉無律(しつむりつ)や全か無かの法則，なんて言ったりします．

つまり，実数値を情報とする現在主流の一般的なニューラルネットワークとは性質が大きく異なることがわかります．

スパイキングニューロンモデル

話は戻ってニューロンモデルについてです．

先ほど話したような神経細胞の本来の働きをモデル化したものを，スパイキングニューロンモデルと言います．
スパイキングニューロンにも「どこまで細かくモデル化」するかによって，いくつかモデルが存在します．
ここでは最もメジャーなLIFモデルについて説明します．

- LIF: Leaky-integrate-and-fire モデル

日本語に直訳すると「漏れ積分発火モデル」です．
積分発火(IF)モデルというものもありますが，IFモデルはその名の通り，入力を積分していって，閾値に達したら発火する，そのようなニューロンモデルです．
一方でLIFモデルはそれに時間的な漏れ (Leak: リーク，減衰)が加わったニューロンモデルです．

LIFモデルの式定義はいくつか見受けられますが，最もシンプルなもので以下のような微分方程式で膜電位を計算します．
$$\tau\frac{dV(t)}{dt} = (-V(t) + E_{rest}) + I(t)$$
このとき，$V(t)$は膜電位，$\tau$は時定数，$E_{rest}$は静止膜電位，$I(t)$が入力電流を指します．この$V(t)$が発火閾値$V_{\theta}$を超えた時，そのニューロンはスパイクを生成する，といった具合です．

この微分方程式を解くとわかりますが，LIFモデルには入力を足し合わせる部分と，時間的減衰が存在します．コードに落とす際には，微小時間でループを回し，以下のような近似した形で実装することが多いようです．

【追記 (2020.04.09)】
以下のコードがちょっと間違っていたのと，少しつまらないコードだったので一部変更しました．

import numpy as np
import matplotlib.pyplot as plt


def lif(currents, time: int, dt: float = 1.0, rest=-65, th=-40, ref=3, tc_decay=100):
    """ simple LIF neuron """
    time = int(time / dt)

    # initialize
    tlast = 0  # 最後に発火した時刻
    vpeak = 20  # 膜電位のピーク(最大値)
    spikes = np.zeros(time)
    v = rest  # 静止膜電位

    monitor = []  # monitor voltage

    # Core of LIF
    for t in range(time):
        dv = ((dt * t) > (tlast + ref)) * (-v + rest + currents[t]) / tc_decay  # 微小膜電位増加量
        v = v + dt * dv  # 膜電位を計算

        tlast = tlast + (dt * t - tlast) * (v >= th)  # 発火したら発火時刻を記録
        v = v + (vpeak - v) * (v >= th)  # 発火したら膜電位をピークへ

        monitor.append(v)

        spikes[t] = (v >= th) * 1  # スパイクをセット

        v = v + (rest - v) * (v >= th)  # 静止膜電位に戻す

    return spikes, monitor


if __name__ == '__main__':
    duration = 500  # ms
    dt = 0.1  # time step

    time = int(duration / dt)

    # Input data
    input_data_1 = 10 * np.sin(0.1 * np.arange(0, duration, dt)) + 50
    input_data_2 = -10 * np.cos(0.05 * np.arange(0, duration, dt)) - 10

    # 足し合わせ
    input_data = input_data_1 + input_data_2

    spikes, voltage = lif(input_data, duration, dt)

    # Plot
    plt.subplot(2, 2, 1)
    plt.ylabel('Input 1')
    plt.plot(np.arange(0, duration, dt), input_data_1)

    plt.subplot(2, 2, 2)
    plt.ylabel('Input 2')
    plt.plot(np.arange(0, duration, dt), input_data_2)

    plt.subplot(2, 2, 3)
    plt.ylabel('Membrane Voltage')
    plt.xlabel('time [ms]')
    plt.plot(np.arange(0, duration, dt), voltage)

    plt.subplot(2, 2, 4)
    plt.ylabel('Output')
    plt.xlabel('time [ms]')
    plt.plot(np.arange(0, duration, dt), spikes)
    plt.show()

((dt * t) > (tlast + ref))は不応期中か否かを見ており，不応期中でなければ膜電位を計算します．上記コードを実行してみると以下のようになります．
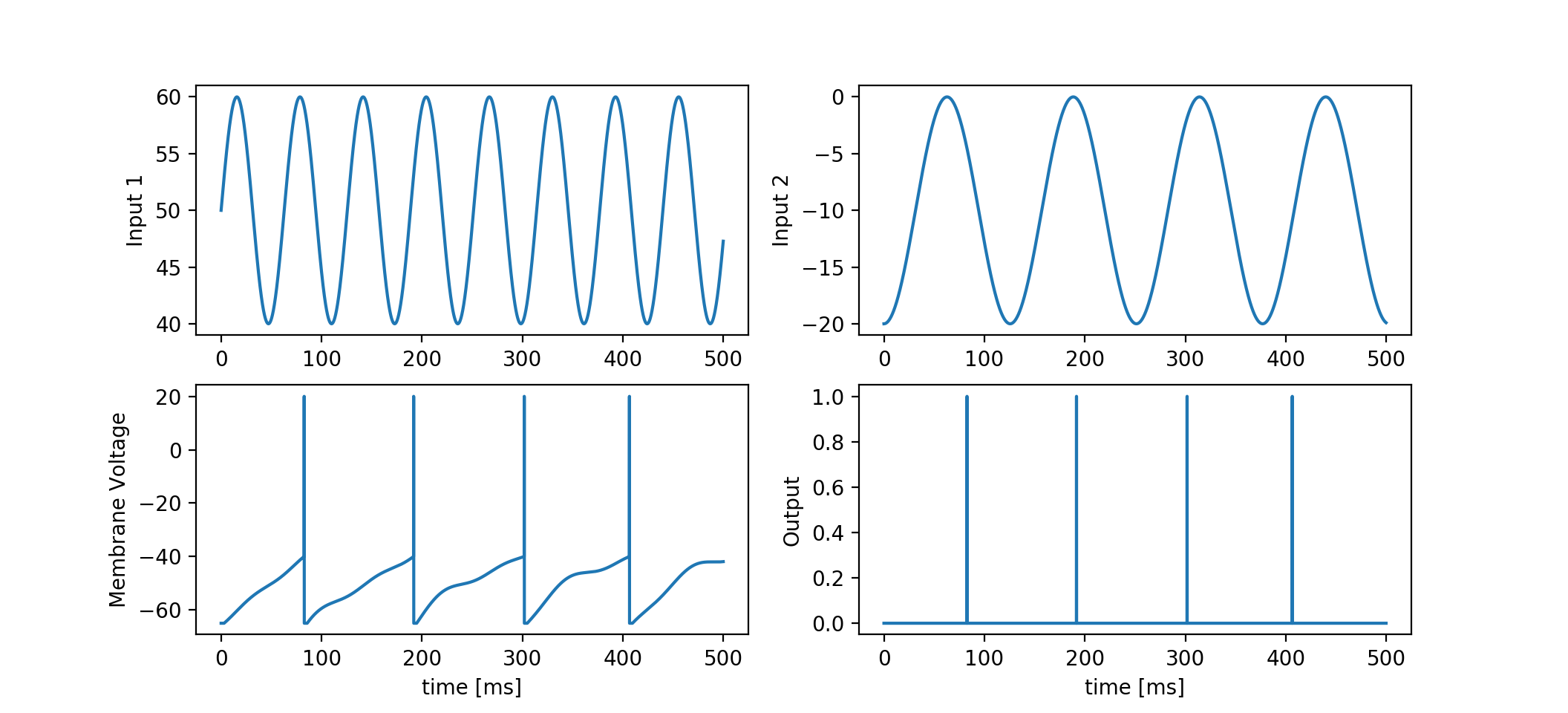
lif_1.png

今回は二つのサインカーブを入力電流としてみました．
一つは活性化させるプラスな入力で，もう一方は抑制性のマイナスな入力です (図上段)．

膜電位の様子と，出力スパイクの関係がわかるかと思います (図下段)．
実際には，受け取る入力はスパイク列(Spike Train)ですので，スパイク列を電流に変換する過程が必要です．

これもやり方は様々ですが，例として以下のようなものが考えられます．
$$I(t)=w\cdot(S(t)*h(t))$$

$$h(t)=(\exp^{\frac{-t}{\tau_1}}-\exp^{\frac{-t}{\tau_2}})$$
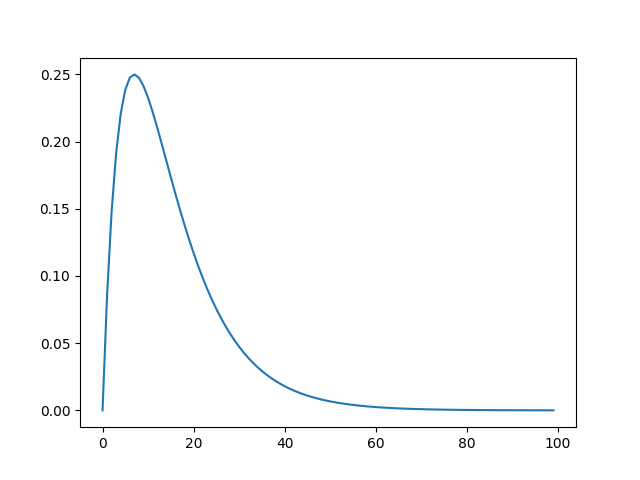
ここで$w$は2つのニューロン間の結合重みです．$h(t)$はいわゆるスパイク応答関数で，スパイクが入力されたときの電流の立ち上がりと減衰を司ります．そして畳み込み演算子によってスパイク列$S(t)$を畳み込む，といった具合です．

最近では，膜電位計算と同じように微分方程式を用いて，単一な指数関数的減衰を畳み込む場合が多く見られる気がします．

実際には入力は複数のニューロンから入ってくるので，$S(t)$は前ニューロンの数だけあり，正しくは前ニューロン数で回すループ(Σ)が入ります．

ちなみに，スパイク応答関数は例えばこんな感じです．

def response(time, tau1, tau2):
    return np.exp((-time/tau1)) - np.exp((-time/tau2))

if __name__ == '__main__':
    times = np.arange(0, 100)
    plt.plot(times, response(times, 10, 5))
    plt.show()

h.png

このような感じで，スパイキングニューロン(LIF)は定義されています．形式ニューロンに比べかなり複雑ですね．

LIFモデルの他にも，かなり細かく定義したHodgkin-Haxley(ホジキン・ハクスレー)モデルや，それを簡易化したFitzhugh-Nagumo(フィッツフュー・南雲)モデルなどがあります．また，LIFにアダプティブな閾値をつけたAdaptiveLIFモデルも最近ではよく使われます．(次に紹介するモデルはこれを使用しています)

有名なモデル(Diehl&Cook)を見てみる

小難しい話は置いておいて，実際の研究を見てみましょう．

以下のモデルは2015年にDiehlらが提案したSNN界では有名なモデルです．
(元論文: Unsupervised learning of digit recognition using spike-timing-dependent plasticity (Diehl et al., 2015))
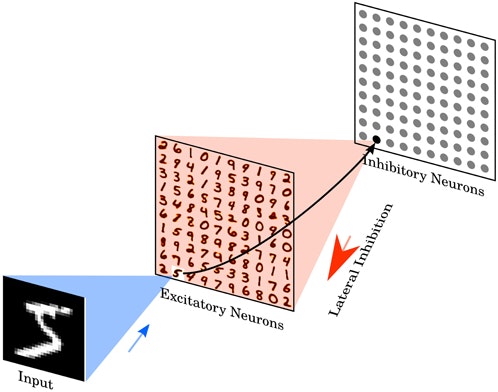
diehl.jpg

ネットワーク構成はとてもシンプルで，入力層，興奮性層，抑制性層の3層構造です．もっと言うと，興奮性層は出力層にあたり，抑制性層は側抑制(Winner-take-all)に相当しますので2層構造です．

このネットワークはSTDP(Spike-timimg-dependent plasticity: スパイクタイミング依存可塑性)学習則と呼ばれる，教師なし学習で特徴抽出を行っています．このSTDP学習則は現存の，どの学習手法よりも生物学的に妥当性のある学習則だと思います．

実際に学習していく様子を見てみましょう．以下のgifは入力層と出力層を結ぶ重みを可視化したものです．1つのウィンドウは28x28で計100個の出力層ニューロンを用意してみました．
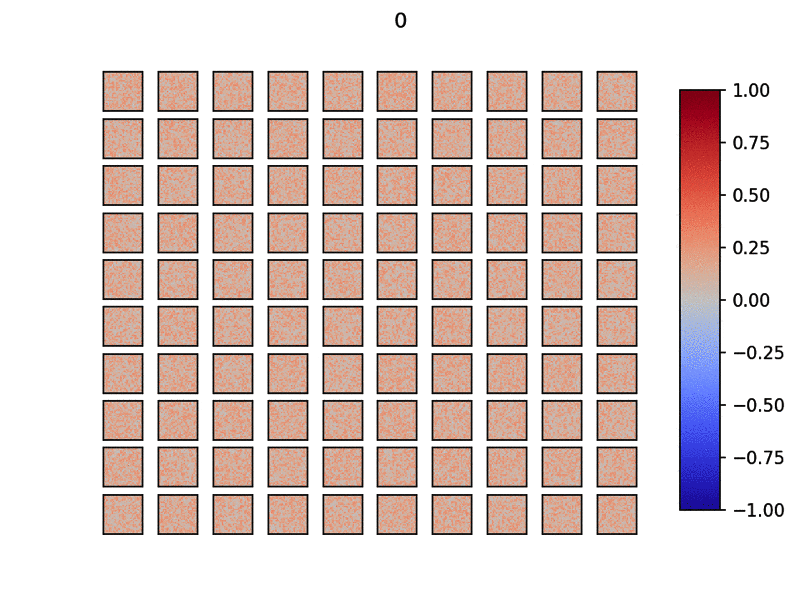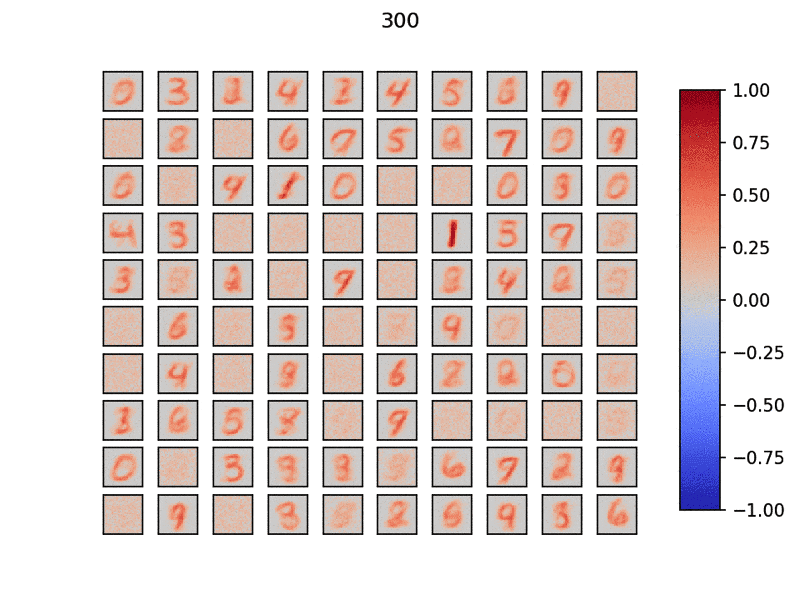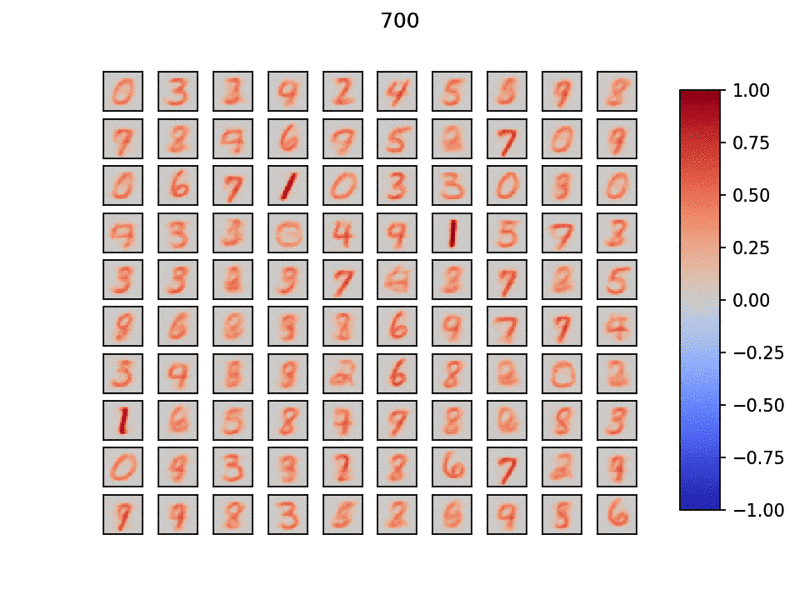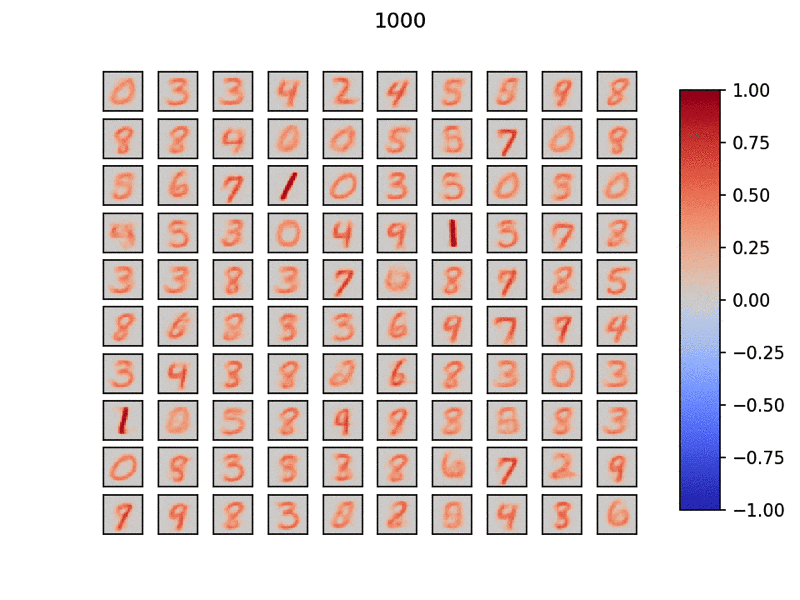
0-1000.gif
タイトルはデータ(MNIST)を流した枚数です．このように分散的にネットワークが特徴を抽出していることがわかります．

ただ，このモデルは少し無理やりな部分もあって，課題はまだたくさんあります．

SNNライブラリ BindsNET

最後はライブラリについて．
SNNのライブラリはなかなか使いやすいものがなかったのですが，最近ではPytorchベースのBindsNETというものが有名になってきました．私も最近使い始め，さらに使いやすくラップしたWBN(WrappedBindsNET)というものをGithubにあげています．動作確認程度なら，ラップしたものの方が使いやすいかと思いますが，如何せん素人がコーディングしていて，常に未完成なのでバグがあっても文句は言わないでください．笑

BindsNET (original): Hananel-Hazan/bindsnet: Simulation of spiking neural networks (SNNs) using PyTorch.
WrappedBindsNET : HiroshiARAKI/snnlibpy: The tiny Spiking neural network library implemented by BindsNet.

Diehlのモデルなら，

from wbn import DiehlCook_unsupervised_model 
DiehlCook_unsupervised_model()

だけで起動します．(要　$ pip install bindsnet)

おわりに

今回マイナーな機械学習分野「スパイキングニューラルネットワーク」について少しだけ概要を紹介しました．これを機にSNNに興味を持ってくれる方が増えると嬉しいです．個人的にはSNNにはロマンが詰まっていると感じます．数十年後にはもしかしたら，より生物学的なSNNが主流になっているかもしれません．

また，もし間違った解釈や説明があればご指摘いただけると幸いです．

興味を持った方は是非色々調べてみてくださいね．日本語文献はとても少ないですが，IBMのスパイキングニューロンをハードウェア化したTrueNorthとかを調べてみるのも良いかと思います．

👉関連記事 : Pythonで実装しながら理解するPoisson Spike (ポアソンスパイク)
👉関連記事 : Hodgkin-Huxleyニューロンモデルを実装してみる

追記

  • 2021.01.04 NEW!
    ゼロから学ぶスパイキングニューラルネットワークをリリースしました．
    これからSNNを勉強しようとしている方向けの完全無料学習サイトですのでぜひ見てみてください！

  • 2020.08.26
    Izhikevichニューロンモデルのシミュレータも作りました．
    こちらは，より脳科学的なニューロンモデルですが，脳科学入門にはとても良いかと思います．
    https://neuron.hirlab.net/

  • 2020.07.02
    Webで動くSpiking Neuron Simuoatorを作ってみました．
    https://spine-web.hirlab.net/
    本当に小規模なシミュレーションしかできませんが，適当に遊んでみてください！

78
58
5

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
78
58