1. はじめに
(2020.05.29 更新:コードと図を良さげなものに変更しました)
(2020.11.05 更新:ごめんなさい.コードが少しだけ間違っていたので修正しました)
脳神経科学や,スパイキングニューラルネットワークの分野ではよく「ポアソンスパイク (Poisson spike)」という単語を目にする.
これは言葉の如く,ポアソン分布にしたがって生成されたスパイク列を指すが...
この考え方は,SNNや神経科学を勉強を始めたばかりの段階では,なかなかイメージしづらくどのように変換が起きているのか分かりづらいものである.
この記事は,そんなマイナー読者に向けたもの. あとは僕自身の備忘録.
(もし間違え・誤解があれば指摘してください...)
2. どこでポアソン分布が登場するのか
まず,そもそも脳神経科学とポアソン分布はどのような関係があるのだろうか?
脳神経細胞は,外界からの入力が無い時でも,自発的に発火を続けるらしく,その発火がポアソン分布に従うと言われている.
ここで,大事なのは「何がポアソン分布」に従うかである.
答えは,「発火周期」.
つまり,スパイクとスパイクの間隔である.
これをまずは前提として頭にいれておく.
3. Poisson Distribution: ポアソン分布
深く理解する前に,前提知識としてポアソン分布を知らなければならない.
知っている人は飛ばして構わない.
ポアソン確率分布は以下の式で示される.
$$P(X=k)=\frac{\lambda^{k}e^{-\lambda}}{k!}$$
導出は割愛するが,この式を言葉で表すなら,
「ある時間中に平均$\lambda$回起こる事象がちょうど$k$回起こる確率」
である.
さらに言い換えるなら**「平均5回起こる事象は,もちろん5回になる確率が一番高くて,そこから離れると確率は下がるよね?」**という至極当たり前なことを示す確率分布だ.
性質としては,平均も分散も$\lambda$になる.
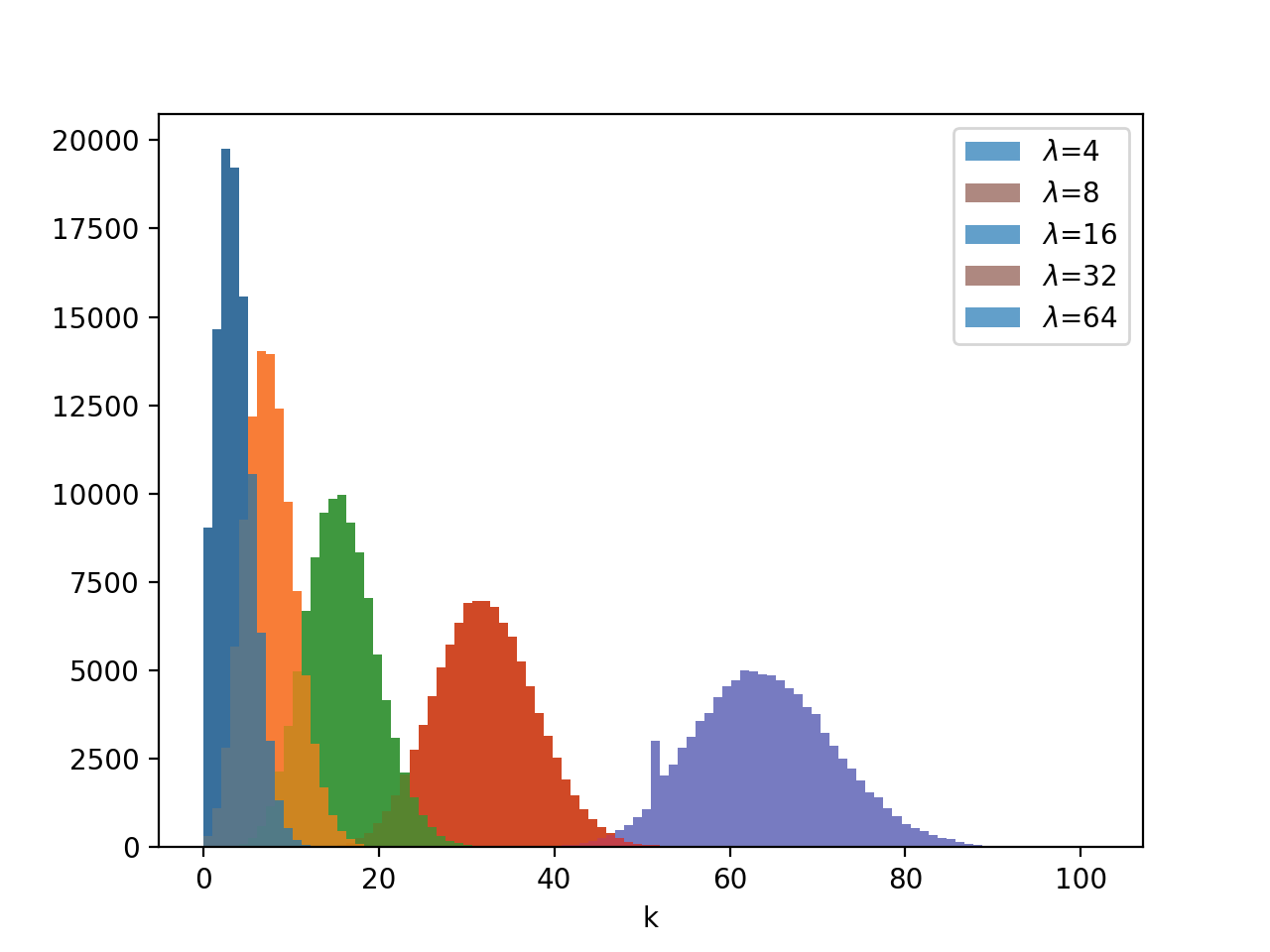
グラフに示すとこんな感じだ.
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
num = 100000 # 抽出回数
lam = [4, 8, 16, 32, 64] # lambda
res = [np.random.poisson(l, num) for l in lam] # Poisson dist. から抽出
for r, l in zip(res, lam):
plt.hist(res, bins=100, histtype='stepfilled', alpha=0.7, label='$\lambda={}$'.format(l))
plt.xlabel('k')
plt.legend()
plt.show()
(なぜか凡例の色とグラフの色があっていないけど,まあ良しとする)
見てわかるように,$\lambda$の値が大きいほど,ガウス分布っぽくなる.
4. ポアソン分布とスパイクの変換
次に,実数値データをスパイクを生成する術を紹介していく.
スパイキングニューラルネットワークの研究では,実世界の実数値データをスパイク列というデジタル信号に変換しなければならない.
それにポアソン分布によるエンコードがよく見られる.
2. どこでポアソン分布が登場するのか で話したように,**ポアソン分布に従うのはスパイク間隔(周期)**である.
したがって,ポアソン分布に渡す$\lambda$は周期 (単位: ms) となる.
しかし,実際には周波数 (Hz) の形に変換してからスパイク列に変換することがほとんどだ.
なぜなら,実数値が大きいほどスパイクがたくさん生成されるのが普通の考えだから.
それを再現するならば,そのまま周期に変換するのではなく,その逆数の周波数から考えた方が良い.
つまり,
- 実数値データを周波数に正規化する
- 周波数から周期に変換する
- 周期をもとに次のスパイクが現れるまでの時間(周期)をポアソン分布から抽出
まだピンとこないかもしれないので実際に実装してみよう.
4.1. 3×3画像からポアソンスパイク列へ変換
試しに,ランダムに生成した3×3の画像をポアソンスパイク列に変換してみる.
コードと実行結果例を以下に示す.(コードを少なくするために脳筋な部分もあるが無視して欲しい)
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
max_freq = 128 # 最大スパイク周波数 [Hz] = 1秒間 (1000 ms) に何本のスパイクを最大生成するか
time = 300 # 観測時間 [ms]
dt = 0.5 # 時間分解能 [ms]
image = np.random.random((3, 3)) # 適当な画像
freq_img = image * max_freq # pixels to Hz
norm_img = 1000. / freq_img # Hz to ms
norm_img = norm_img.reshape(-1) # 2次元だと扱いが面倒なので1次元に
spikes = [
# 周期が抽出されるのでスパイク発生時間としては累積させなければならない
# とりあえず,今回は約300msに収まる分だけ抽出
np.cumsum(np.random.poisson(cell / dt, (int(time / cell + 1)))) * dt
for cell in norm_img
]
# Plotting
plt.figure(figsize=(14, 4))
# Original Image
plt.subplot(1, 2, 1)
plt.title('original')
plt.imshow(image, cmap='gray')
plt.colorbar()
for num in range(9):
plt.text(int(num%3), int(num/3), str(num), color='tab:blue', fontsize=14)
# Spike trains generated by Poisson Encoder
plt.subplot(1, 2, 2)
plt.title('Spike firing timing')
for i, s in enumerate(spikes):
plt.scatter(s, [i for _ in range(len(s))], s=1.0, c='tab:blue')
plt.xlim(0, time)
plt.ylabel('pixel index')
plt.xlabel('time [ms]')
plt.show()
出力結果を見ると,生成されたポアソンスパイク列は,おおよそ同じ周期で発火しているように見える.
これが,ポアソンスパイク列ないしポアソンスパイクエンコーダ (Poisson Spike Encoder) の概要である.
やはり少しややこしい.
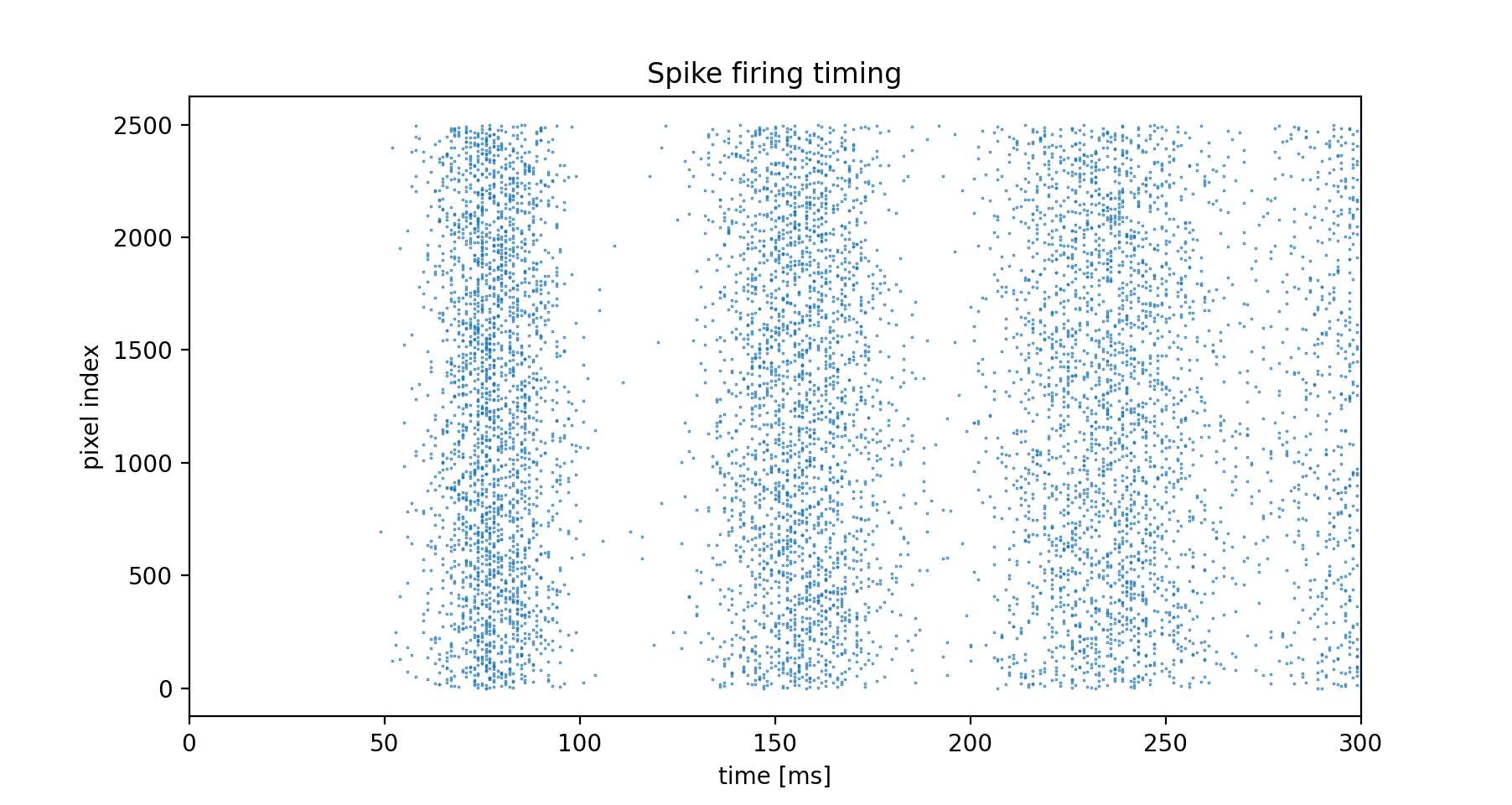
ちなみに50×50で,かつ全て同じ画素値(0.1)で生成してみると,以下のように周期性が分かりやすく観察できる.
追記: わかりにくいコードの補足コメント
spikes = [
# 周期が抽出されるのでスパイク発生時間としては累積させなければならない
# とりあえず,今回は約300msに収まる分だけ抽出
np.cumsum( # 累積
np.random.poisson( # |- Poisson分布から次の発火時刻までの時間を抽出
cell / dt, # |-- λとして周期を与える (が,int型しか無理なのでdtで一旦割る)
(int(time / cell + 1)) # |-- 300msに収まる分だけ抽出 (余分に1つ追加で抽出) ← 脳筋ポイント!
)
) * dt # 最後にfloatに戻す
for cell in norm_img # 各ピクセルごとに算出
]
5. あとがき
脳神経科学とかスパイキングニューラルネットワークの記事ってQiitaでは多分需要はほとんどないんだろうけどドメインが強いから,長期スパンで見たらそこそこ需要がありそうなので,この分野の記事をちょくちょく書いています.
今回はポアソンスパイクについて.
この話は,僕もずっと勘違いしていたもので,いまだにあっているか不安になります.
でも,きっとこの分野を学びたての人は,理解しがたい話ではあるので,そういった人の役に立てば幸いです.
もし,「Python」のタグからこの記事にたどり着いた人は,興味あれば以下の記事も読んでみてください.
👉 Spiking Neural Networkとは何なのか - Qiita
