ハイどうもこんにちは!
前回に引き続き位置ベースなんちゃって物理で遊んでいきます。今回は導き出された位置を直接操作し、制約条件を加えていきます。
さっそく始めていきます!
ところで、ここまで扱ってきた位置、速度、力などはすべて3次元ベクトルです。シレっとベクトルの足し引きなど扱ってきましたが、今回から正規化とか内積とかよう分らんものも出てきます。気が向いたら以下の記事などで理解を深めておくと良いかもしれません!スルーしてもBifrostグラフは組めます。たぶん!
点と点の距離を一定に保つ
点と点の距離を保つといっても大きく分けて2種類あります。
- 2点のうち1点が固定 → 1点だけ動かせばいい
- 2点の両方がフリー → 2点とも動かす必要あり
前者の方が簡単なのでまずは片方が固定の場合からいきます。
片方が固定の場合
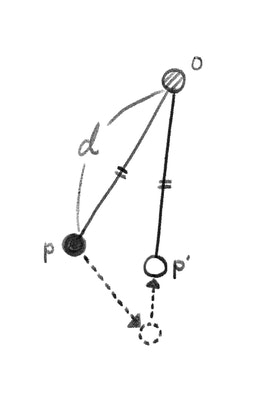
補正したい点を$p$、固定されている点を$o$として、$p$と$o$の間の距離を$d$に保ちたいとします。もし間の距離がずれていた場合、次の式で$p$のみを補正し、指定した距離に引き戻すことができます。
p' = o + \frac{p - o}{\| p - o \|} d
$\frac{p - o}{| p - o |}$は$o$から$p$へ向かうベクトルを正規化(長さを1に)したものです。正規化ベクトルに本来の長さを掛け、固定点の位置に足しています。方向だけは維持しつつ長さだけ強引に戻してしまう形になります。
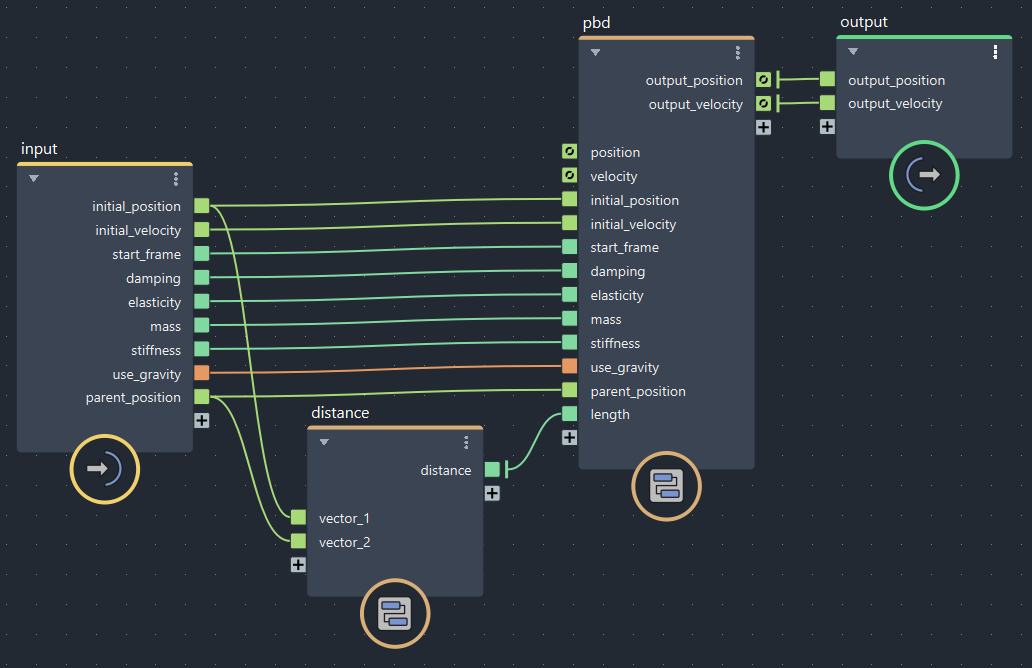
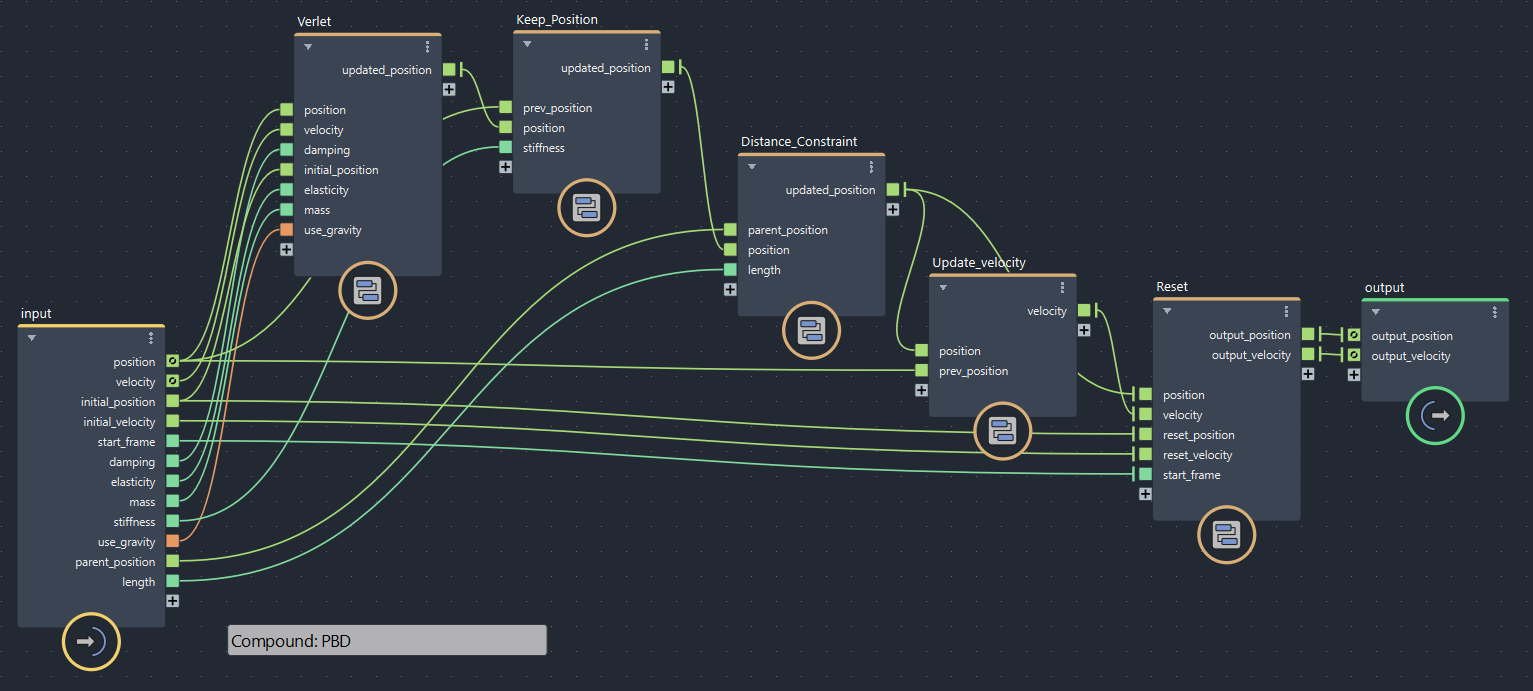
Bfrostグラフは前回の最後のものから始めます。Distance Constraintが追加した部分です。制約は絶対!なので計算箇所は最後のほうになります。速度更新の直前ですね。
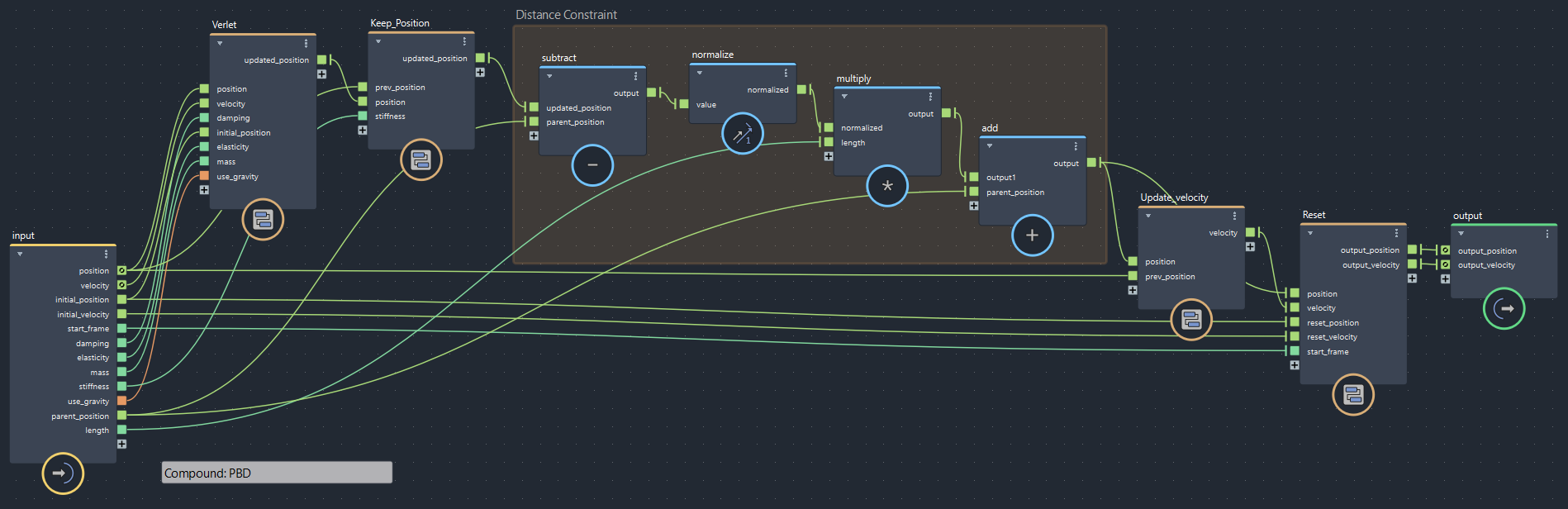
▲bifrostGraphShape > pbd
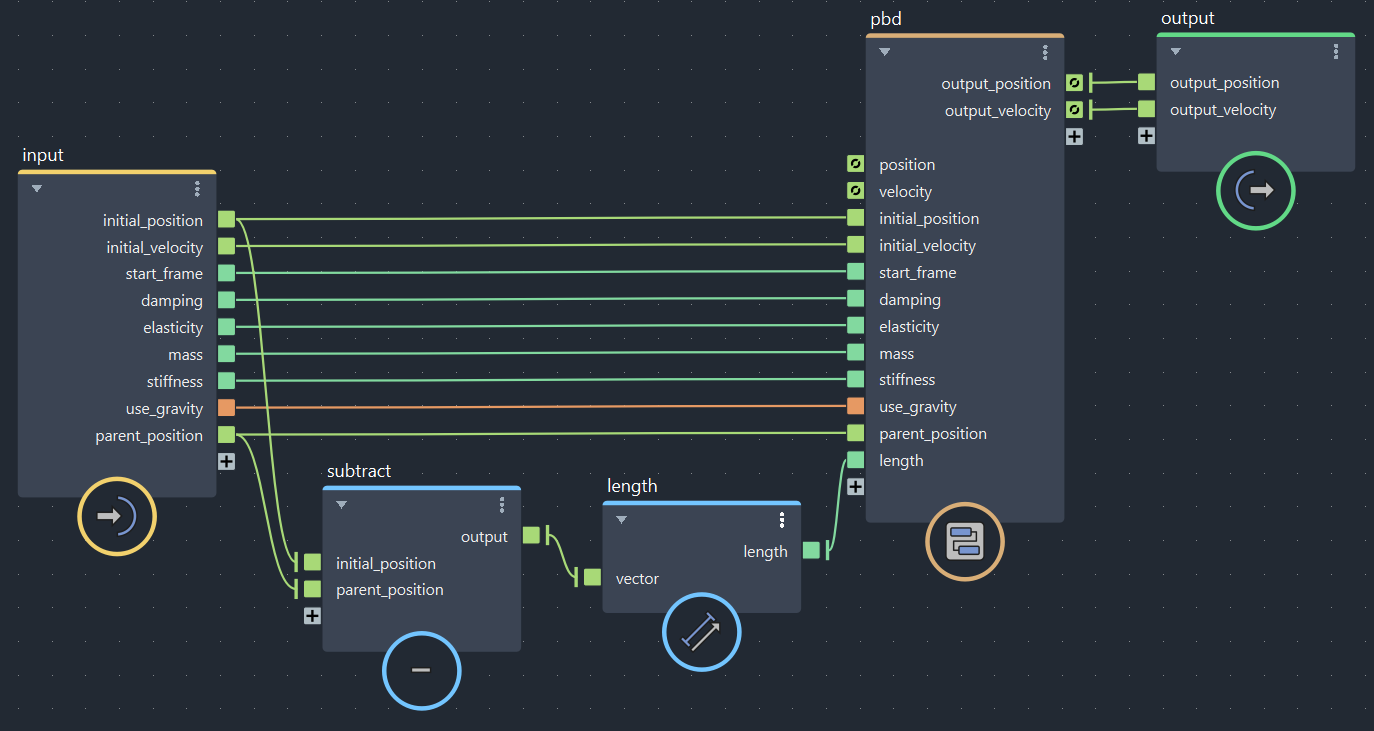
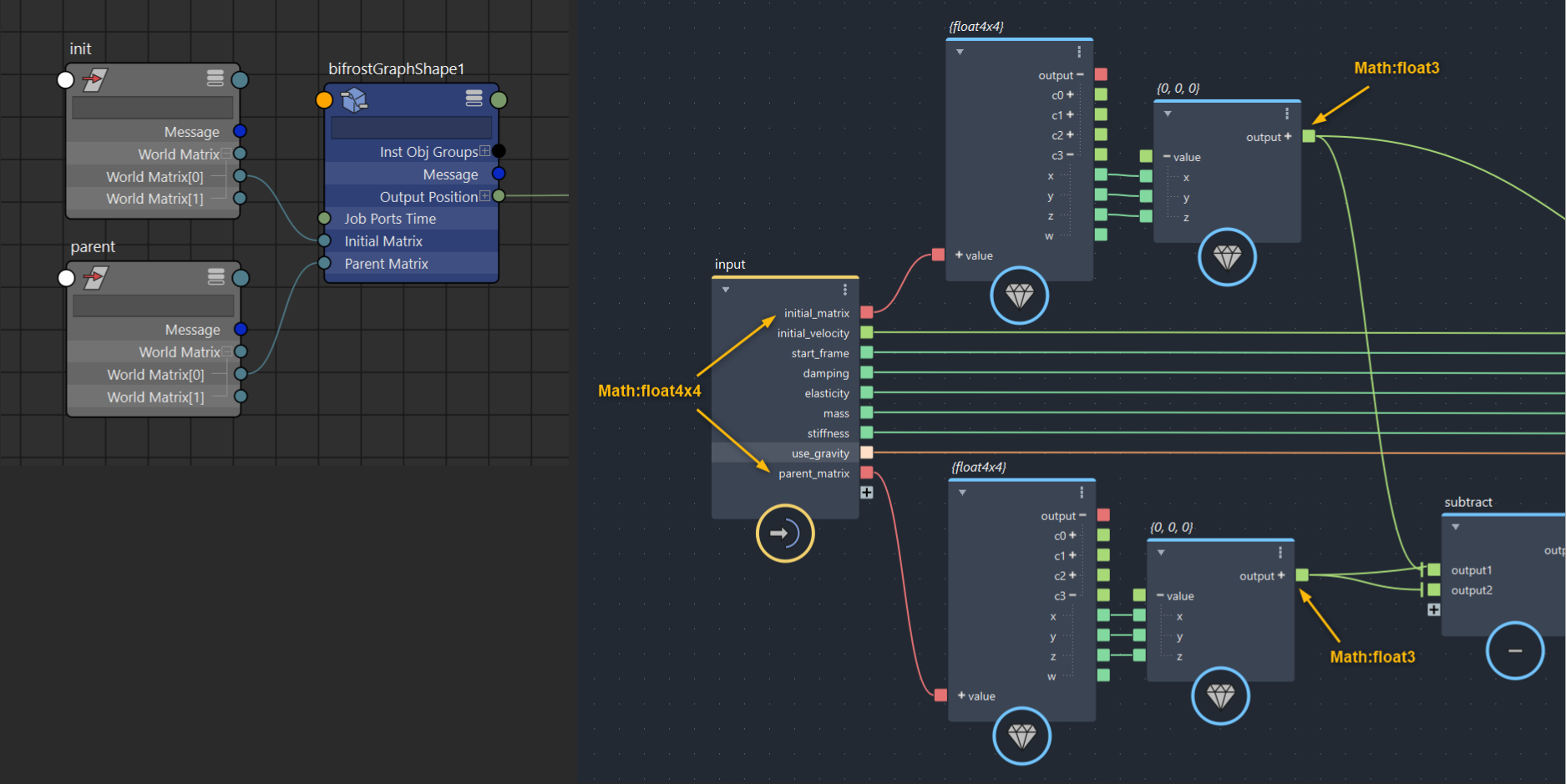
▲bifrostGraphShape(長さは外側で事前に計算しておきます)
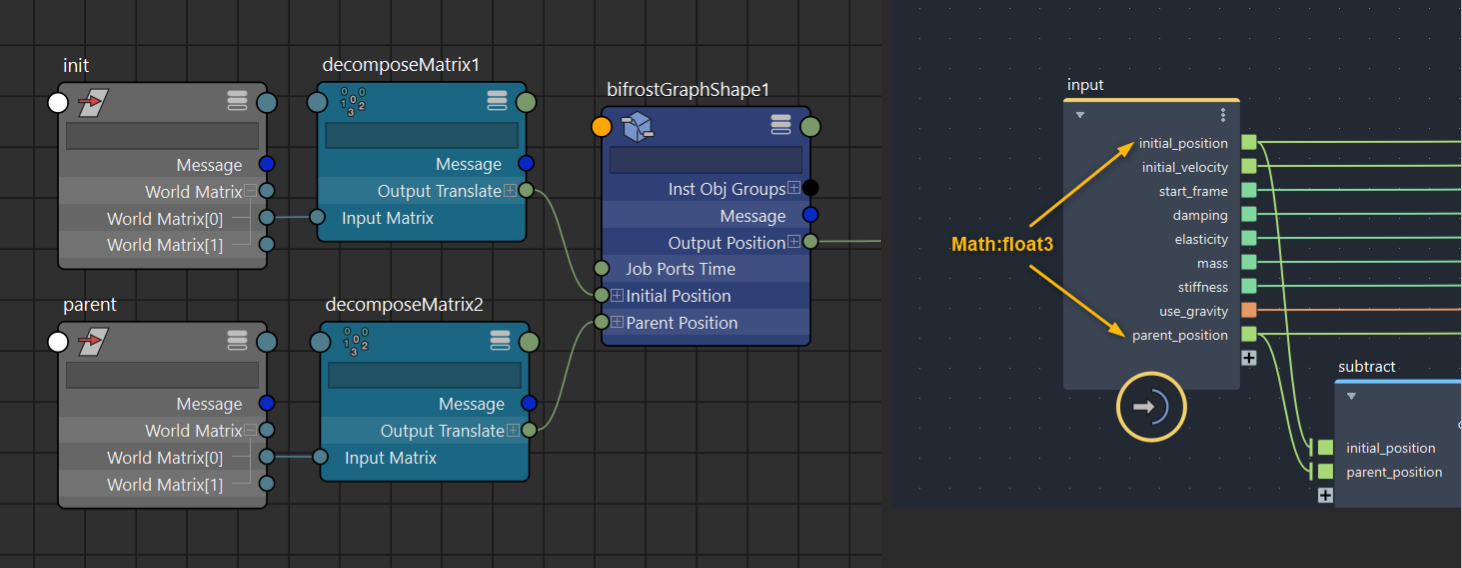
固定されている点としてロケーターを新たに作成し、Parent Positionに接続しておきます。
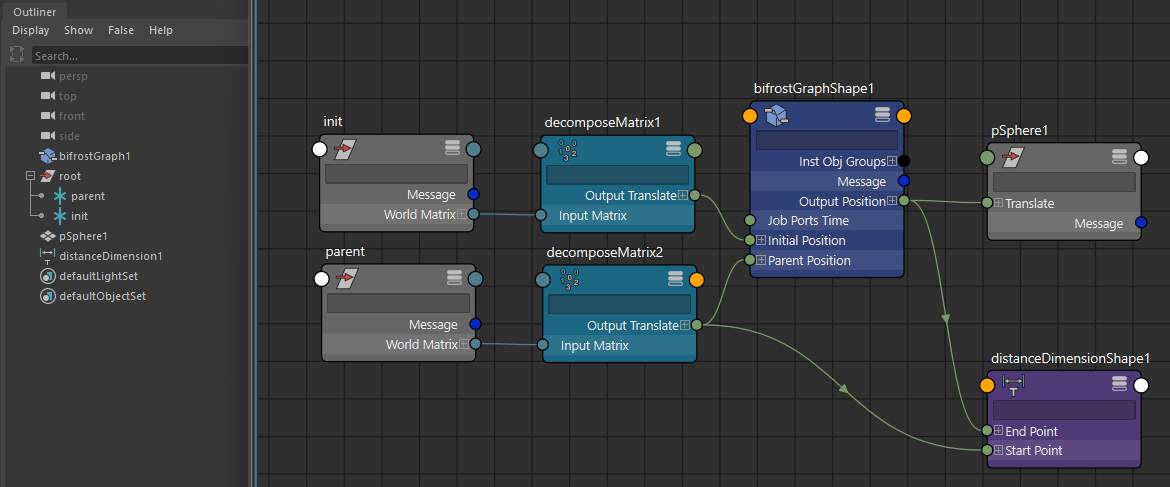
▲parentが固定点
再生すると、前回までの重力やバネなどの影響は生きたまま、固定点から長さを一定に保ち回転するような動きになりました。
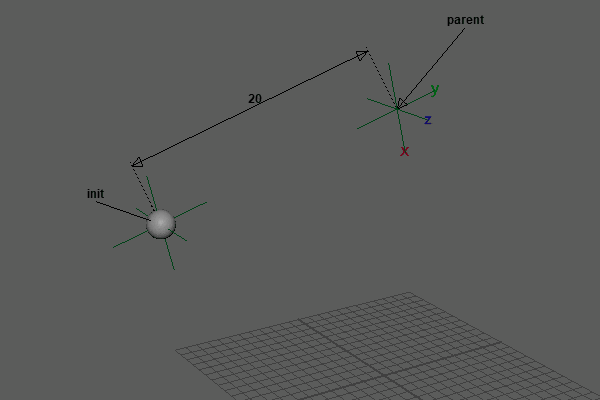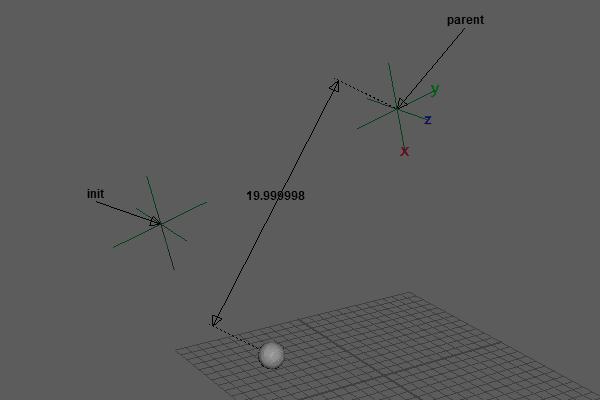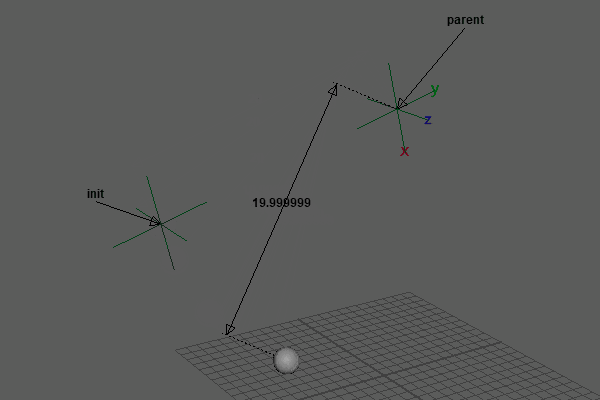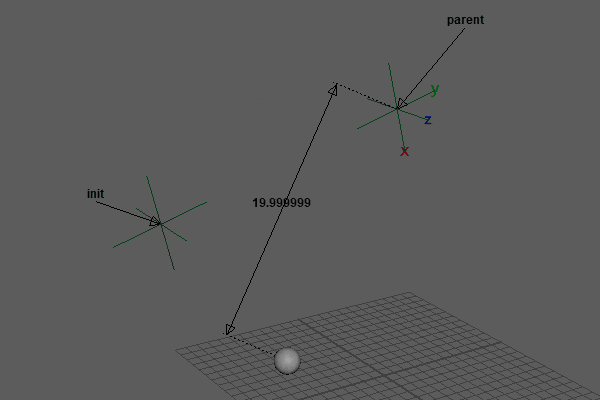
実際に、この2点を連ねていくとなんだか見覚えのあるボーンダイナミクスが出来上がります。これについては後の回で取り上げます。
両方がフリーの場合
このケースはこちら(Position Based Dynamics)の論文から計算式を拝借してきます。
2つの点$p_1, p_2$の間の距離を$d$に保ちたいとします。$\Delta p_1, \Delta p_2$がこれから求めたい各点の移動量で、それぞれどれだけ動かせば$d$になるか、という式です。
\displaylines{
\Delta p_1 = - \frac{w_1}{w_1 + w_2}(\|p_1 - p_2\| - d) \frac{p_1 - p_2}{\|p_1 - p_2\|} \\\
\Delta p_2 = + \frac{w_2}{w_1 + w_2}(\|p_1 - p_2\| - d) \frac{p_1 - p_2}{\|p_1 - p_2\|} \\\
w_i = \frac{1}{m_i}
}
$\frac{w_1}{w_1 + w_2}, \frac{w_2}{w_1 + w_2}$は正規化済み(合計を1にしてある)ウェイトです。2点の質量が同じだとするとここはどちらも$\frac{1}{2}$でいいのですが、重さが違う場合は重い方がウェイトが小さくなり動きにくくなります。$(\|p_1 - p_2\| - d)$ は今の2点間の距離と$d$の差分、$\frac{p_1 - p_2}{\|p_1 - p_2\|}$は正規化したベクトルです。距離差分を重さに基づいて2点で分け合い、それぞれがお互いの方向に移動する、ということになります。
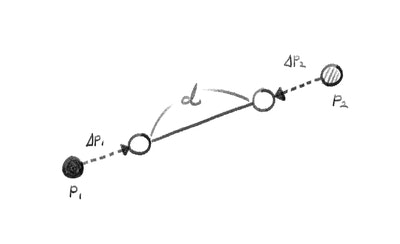
2点がフリーなので、まずこれまでの処理を適用した2点を用意します。前回の最後のBifrostグラフから始め、pbd内のノードをまるっと複製して2点分の計算が出来るようにしておきます。position, velocity, massだけは入力を共有せずしっかり分けておきます。
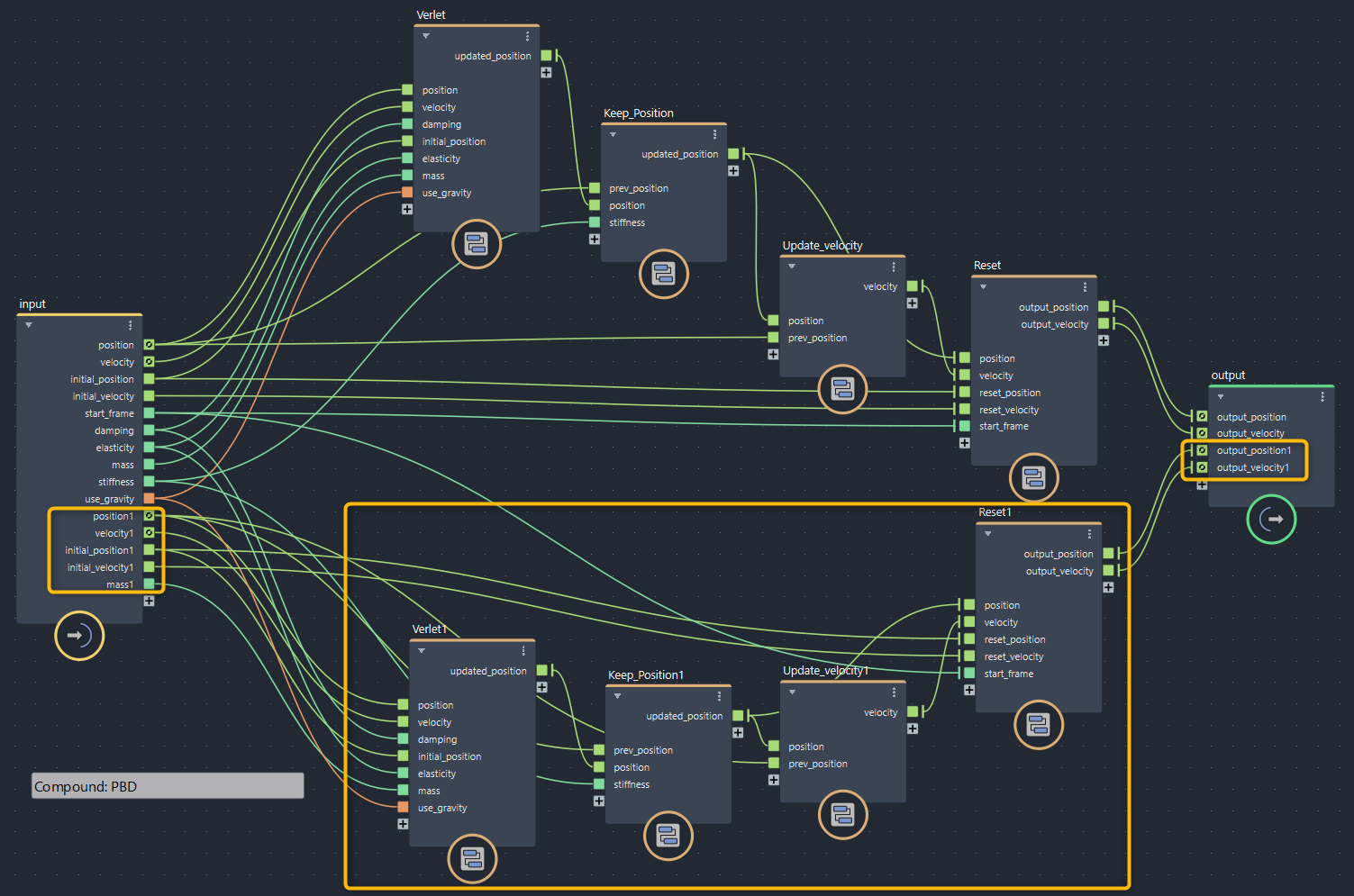
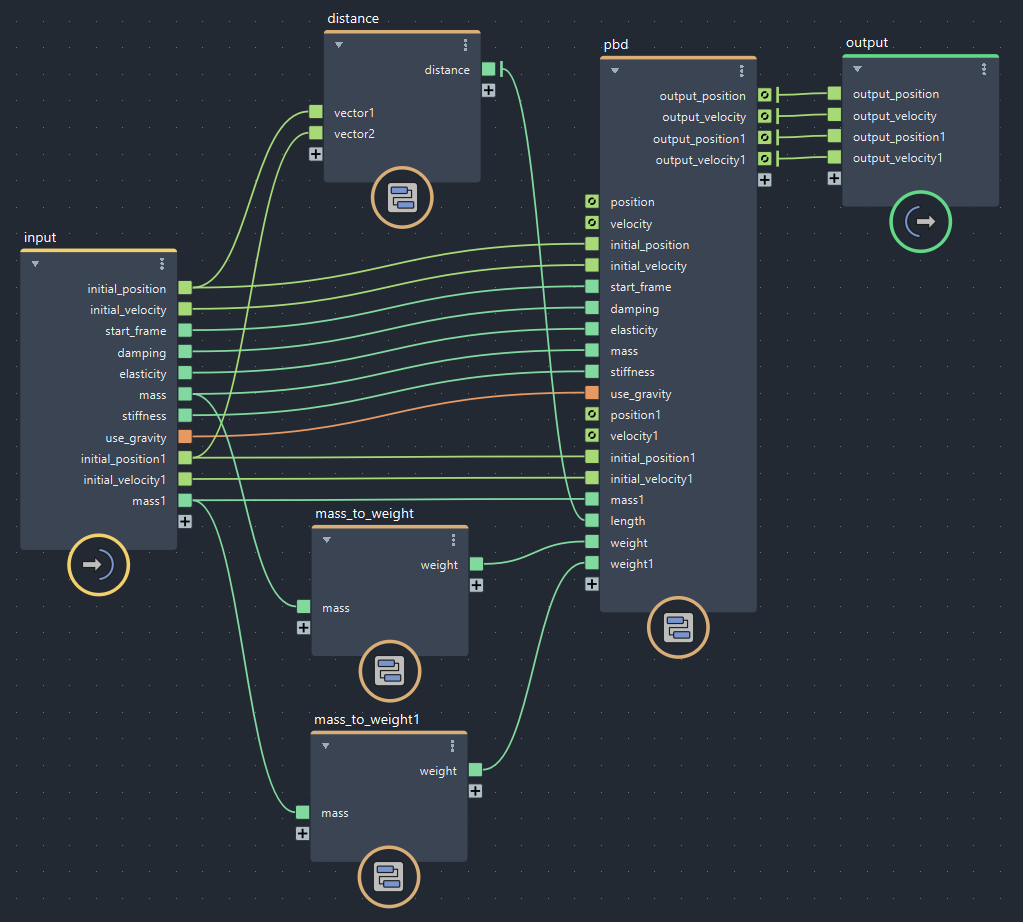
▲bifrostGraphShape > pbd(黄色い枠が増やした部分)
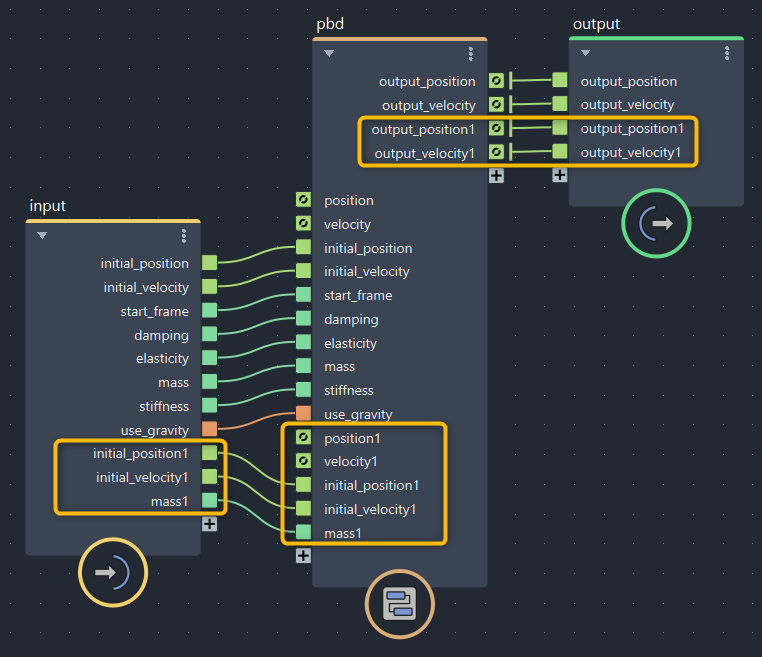
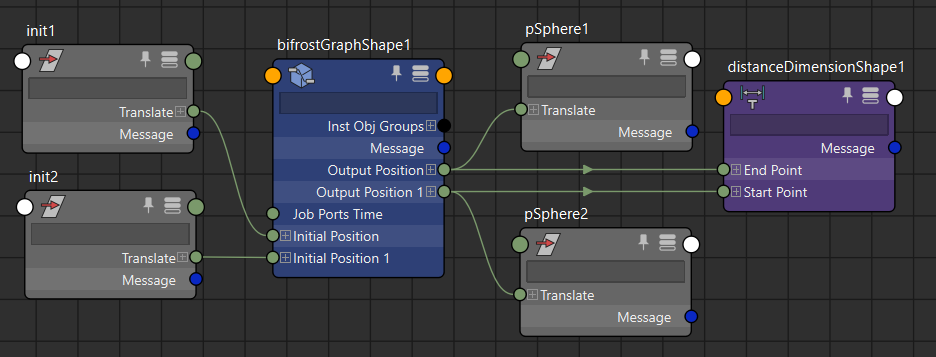
▲bifrostGraphShape(黄色い枠が増やした部分)
再生するとこのような状態になります。どちらの点も初速度を0、dampingを0.1、elasticityを30、stiffnessを0、massだけ差をつけていて、左を1.0、右を0.3、にしてあります。当然ですが複製しただけなので2点間の距離は変化します。
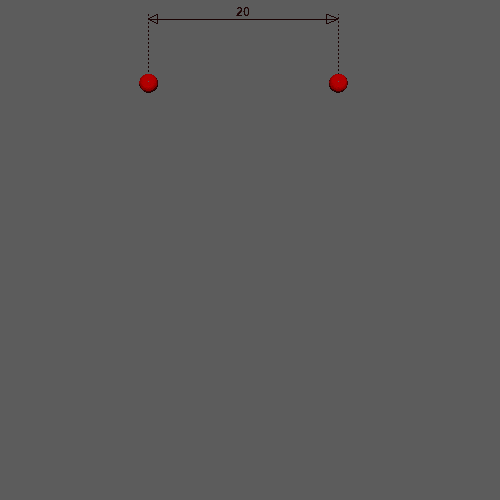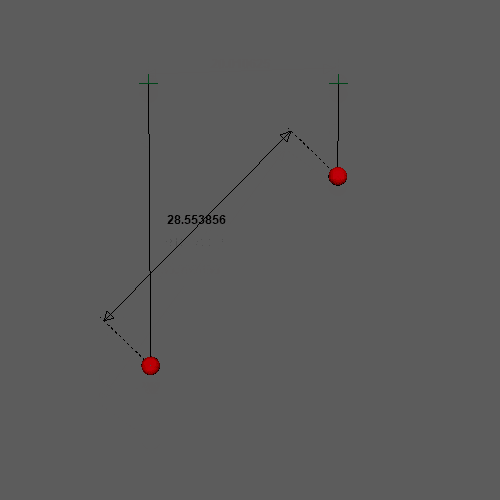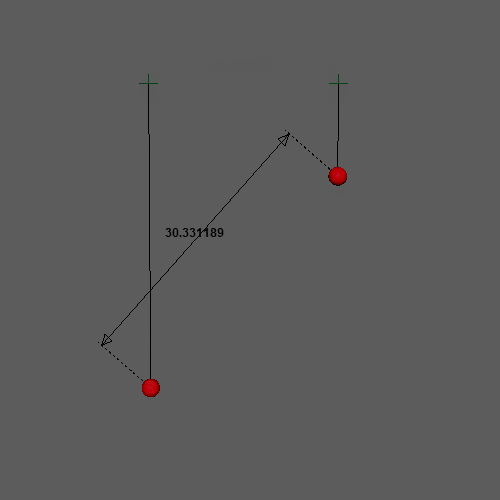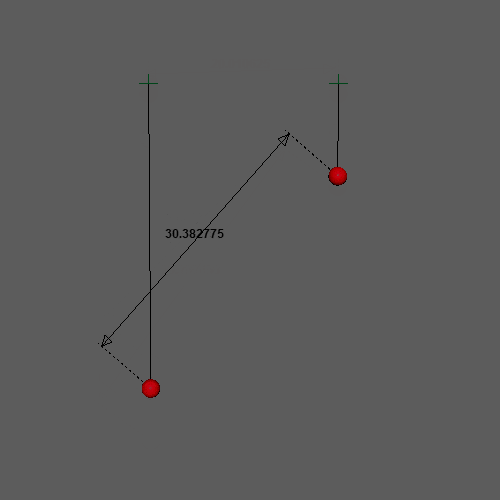
ここから前述の式を元に距離制約を追加します。
まずpbdの外側で2点間の距離$d$とウェイト$\frac{1}{m_1}, \frac{1}{m_2}$を事前計算します。
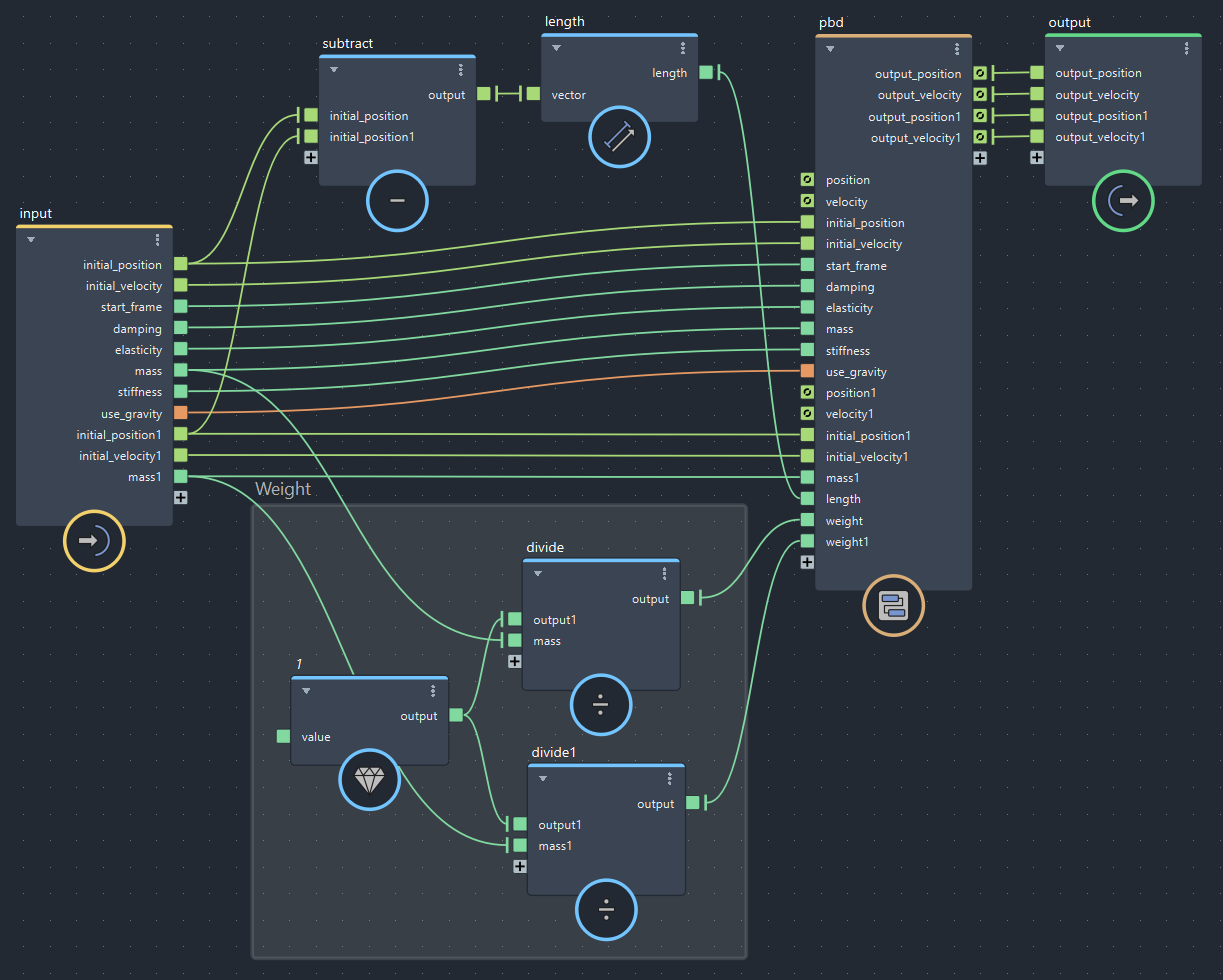
▲bifrostGraphShape
制約は絶対!なので2点の位置更新が終わったところで距離制約を挟み込みます。追加したのはDistance_Constraint_2というコンパウンドです。
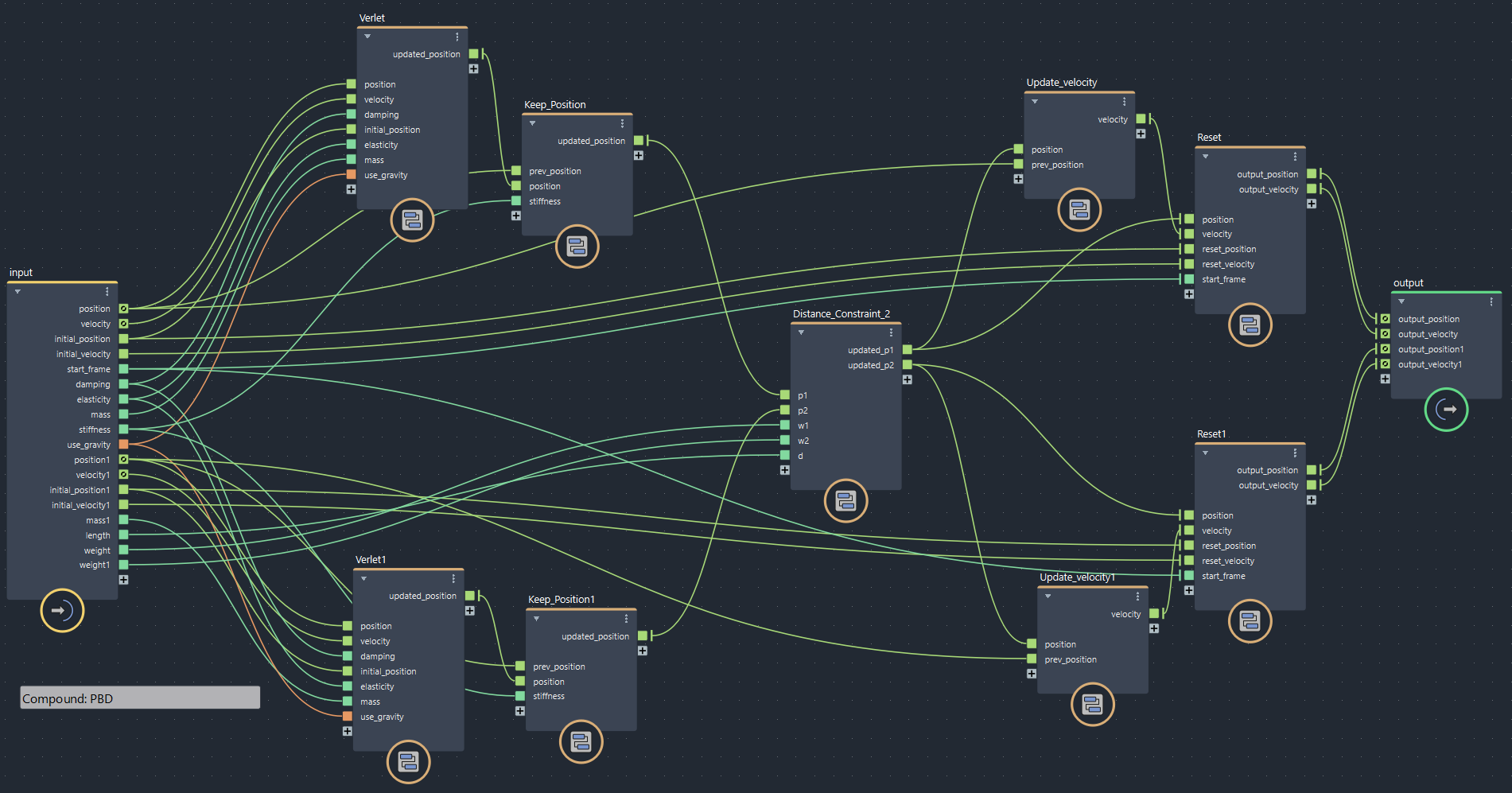
▲bifrostGraphShape > pbd
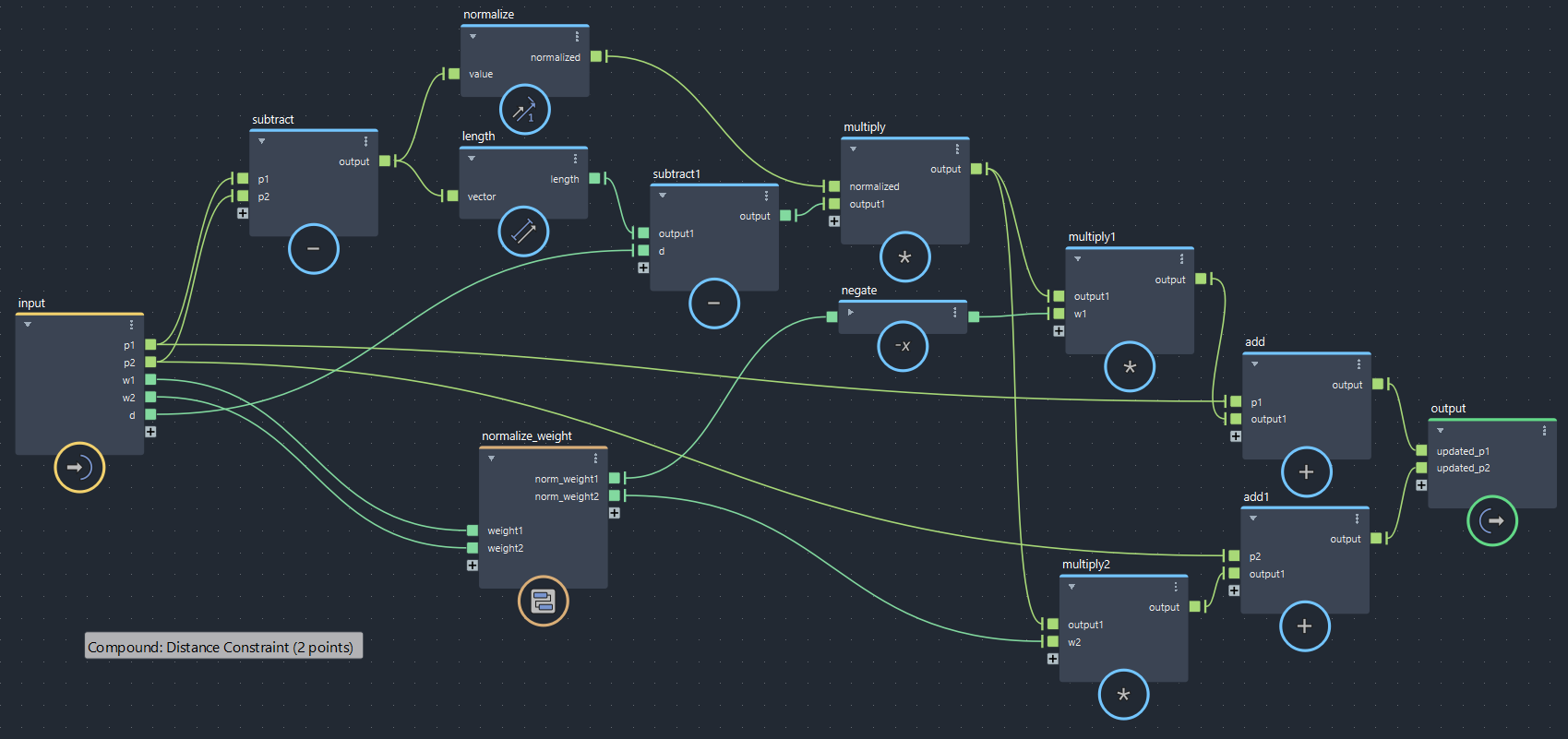
Distance_Constraint_2の中身はこのようになってます。前述の式と、得られた$\Delta p_1, \Delta p_2$を元の位置に足して更新するところまでが含まれています。
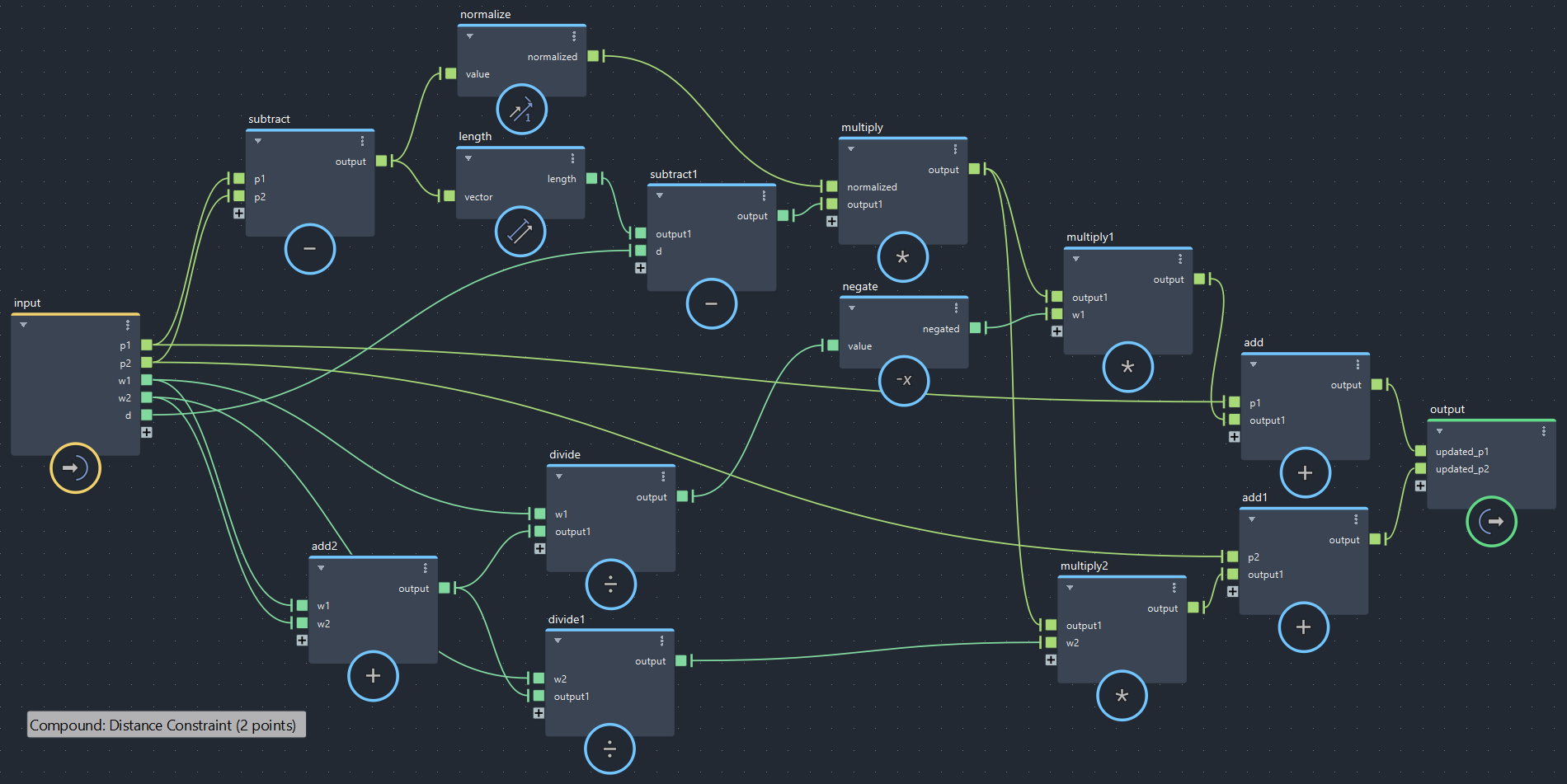
▲bifrostGraphShape > pbd > Distance_Constraint_2
再生すると、このようになりました。重力、バネ、質量の差、距離制約がすべて表現できていそうです!
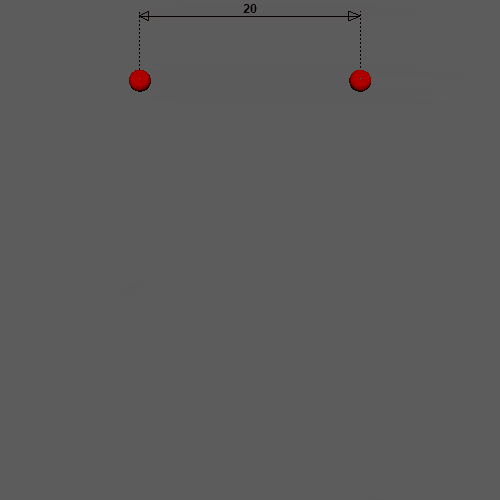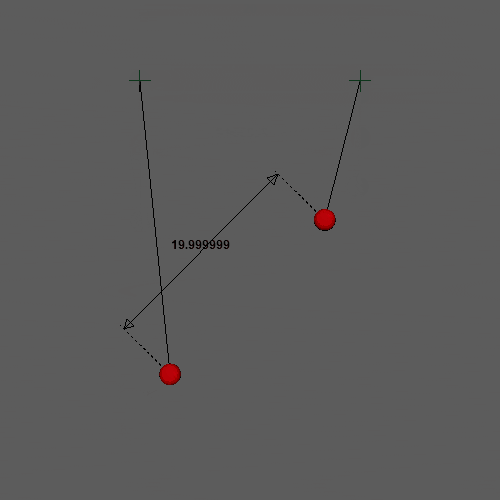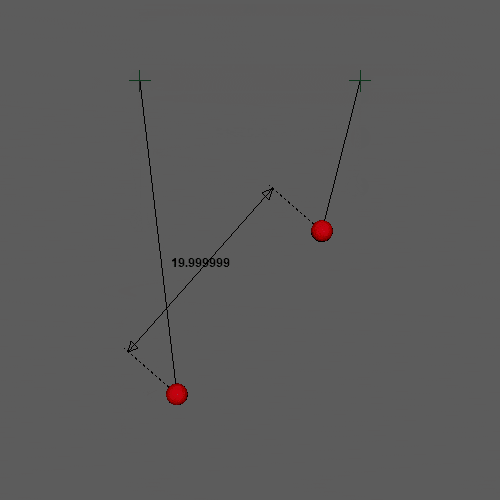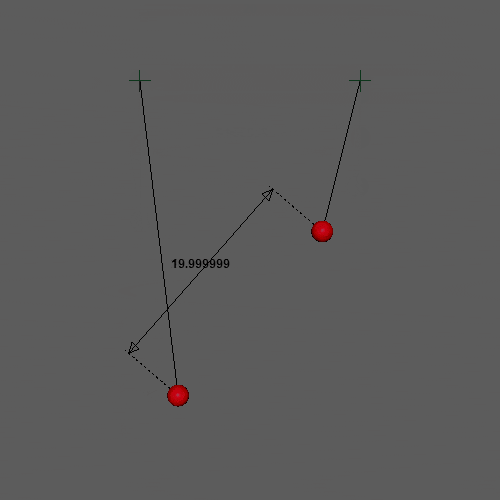
今回の「制約条件」は位置ベースの便利なところが最も現れているところな気がします。物理的な正しさからは離れていきますが、単純で扱いやすいのがメリットです。次回はコリジョンを追加します!
今回のグラフまとめ
片方が固定
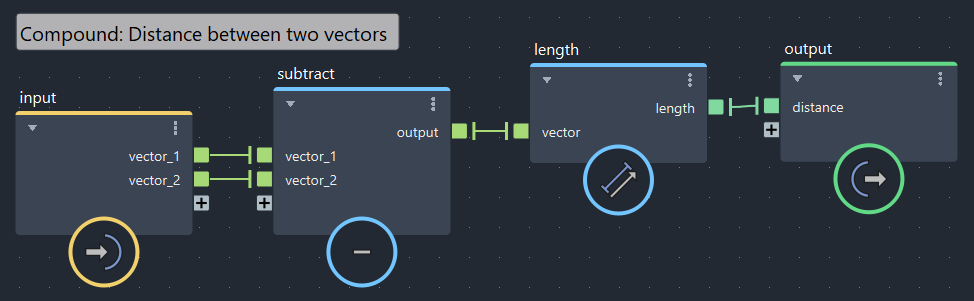
2つのベクトル間の距離を計算(bifrostGraphShape > distance)
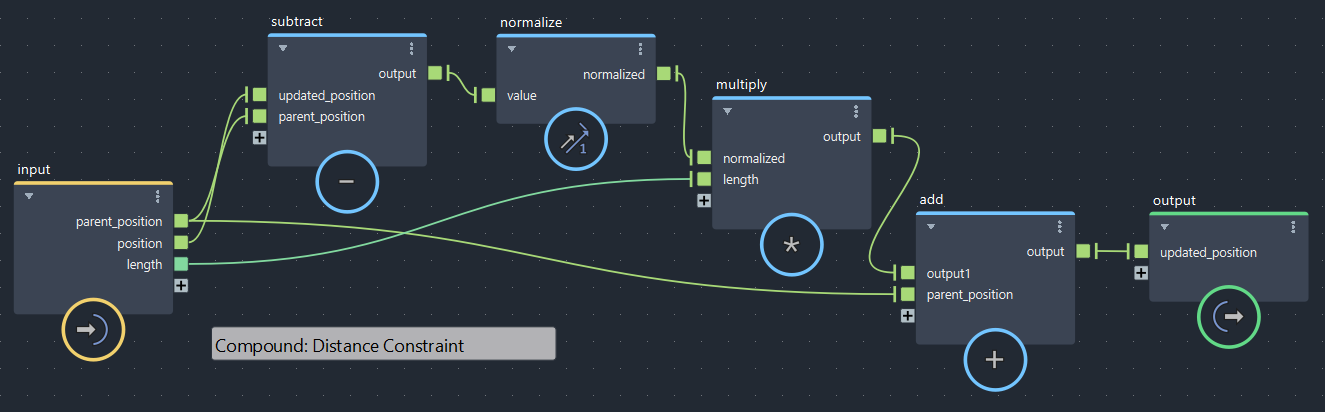
距離制約①:片方が固定(bifrostGraphShape > pbd > Distance_Constraint)
両方がフリー
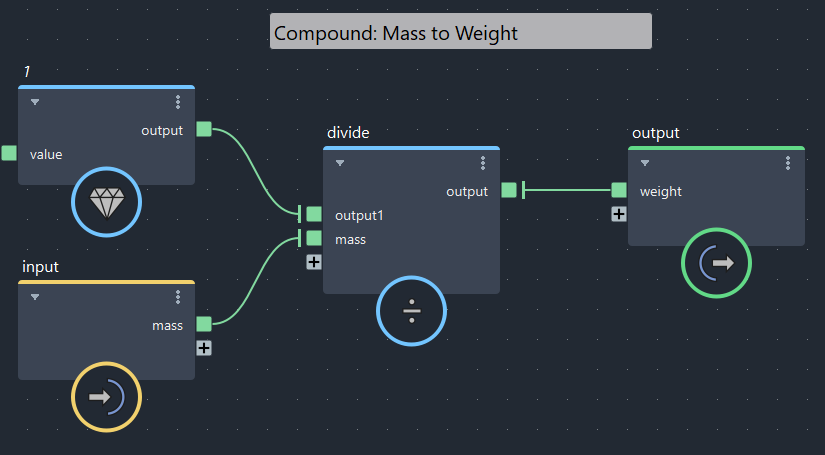
質量からウェイトを計算(bifrostGraphShape > mass_to_weight)
距離制約②:両方がフリー(bifrostGraphShape > pbd > Distance_Constraint_2)
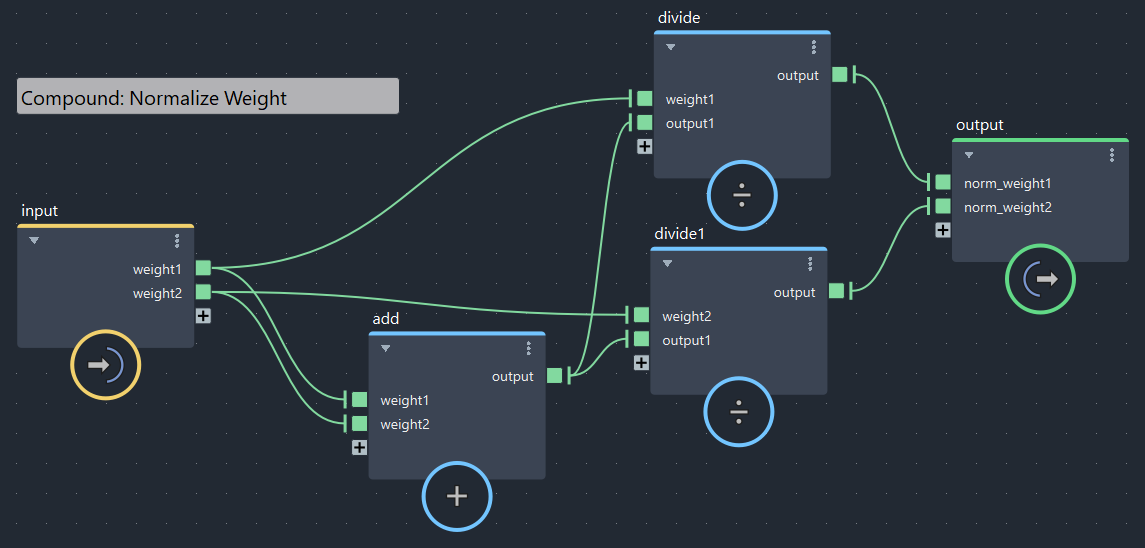
2つのウェイトの合計が1になるように正規化(bifrostGraphShape > pbd > Distance_Constraint_2 > normalize_weight)
だんだんコンパウンドが溜まってきたので、今後も使うものはPublishして保存しておくと便利かもしれません!
参考🔗:#09 コンパウンドにしてチームで共有! | プラチナゲームズ公式ブログ
前の記事
次の記事