ハイどうもこんにちは！
前回に引き続き位置ベースでなんちゃって物理をいじくっていきます。
\begin{cases}
v(t) = \frac{x(t) - x(t - \Delta t)}{ \Delta t} \\
x(t + \Delta t) = x(t) + v(t) \Delta t +\frac{F}{m} \Delta t^2
\end{cases}
前回、見なかったことにした$\frac{F}{m} \Delta t^2$の部分と、さらにその後、得られた位置を強引に補正する工程を追加していきます。ベースのBifrostグラフは前回組んだものがあるのでちょい足しするだけです。
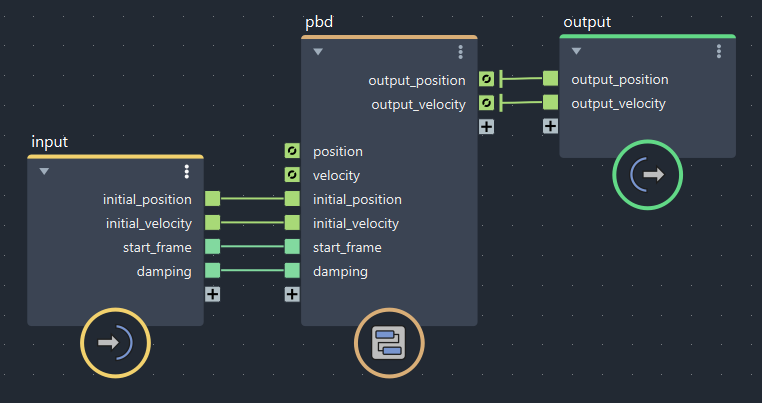
が、その前に、初期値をvalueノードで入力するのは面倒になってきたのでinputにつなぎ直しておきます。前回の最後のグラフから始めます。
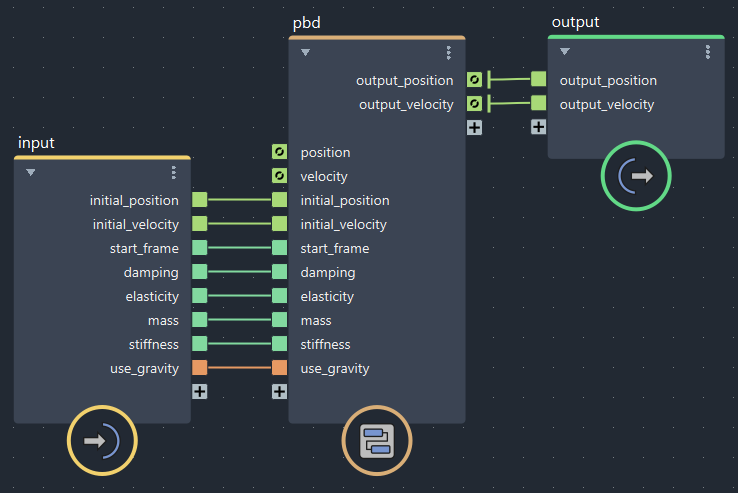
inputとoutput以外の全体をコンパウンド化し、以下のように修正します。入力側のフィードバックポートには何も接続してなくて大丈夫です。（接続してもすぐ上書きされます。）出力側のフィードバックポートはしっかりoutputへつないでおきます。
▲bifrostGraphShape
▲bifrostGraphShape > pbd
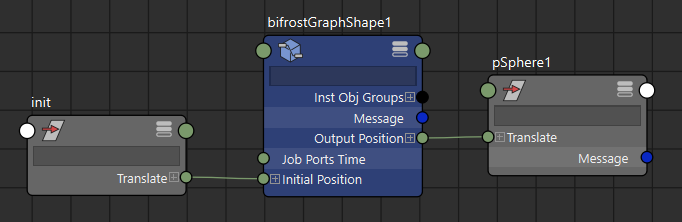
▲Initial Positionへlocatorなどを接続し、初期位置を自由に動かせるようにしておきます
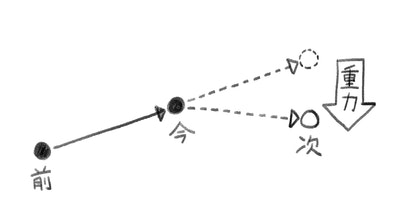
重力
では本題に戻って重力を足してみます。まず、$\frac{F}{m} \Delta t^2$の$m$は質量、$F$は力、$\Delta t$は前回も書きましたが1ステップの経過時間です。「力（チカラ）ってなんやねん…」と思うかもしれませんがこれも位置や速度と同じくベクトルで表されます。単位は$N[kg \cdot m/s^2]$ですが、まぁ細かいことは気にせず進めましょう。
重力による力は次のように表されます。
F_{gravity} = mg
$g$は重力加速度です。このことから例の式の$\frac{F}{m} \Delta t^2$の部分は次のように置き換えられます。
g \Delta t^2
$g$はどんな質量のものでも約$9.8 [m/s^2]$が標準値とされているので、Y軸下向きにこれをあてはめます。
g = (0, -9.8, 0)
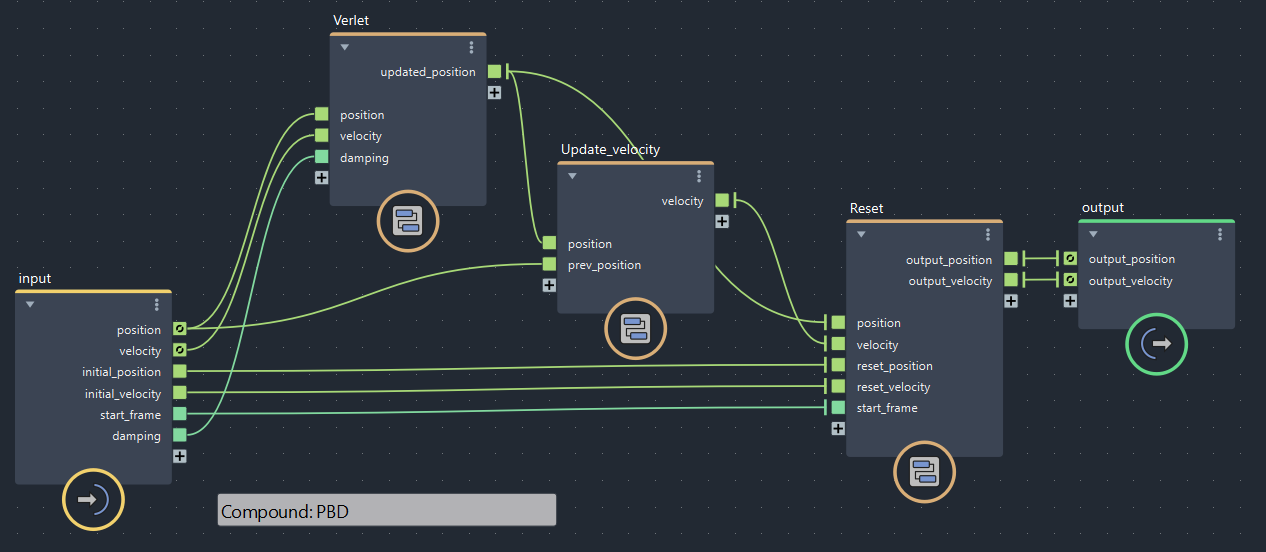
ということで、Bifrostグラフに追加します。右下のGravityが追加した部分です。
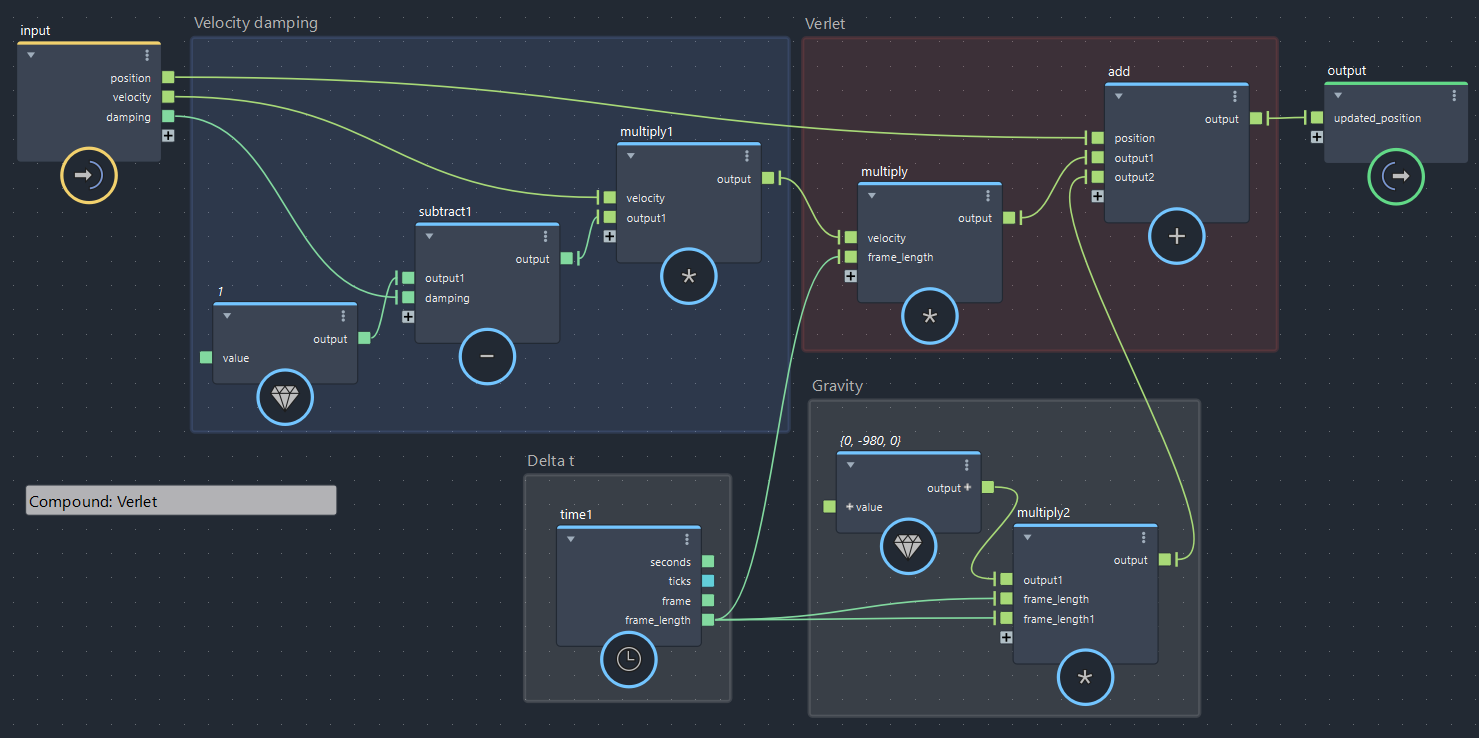
▲bifrostGraphShape > pbd > Verlet（※現在シーンの単位がcentimeterなので-980にしてあります）
初期位置を上空5m（500cm）、初速度を0、dampingを0にして30fpsで再生してみます。
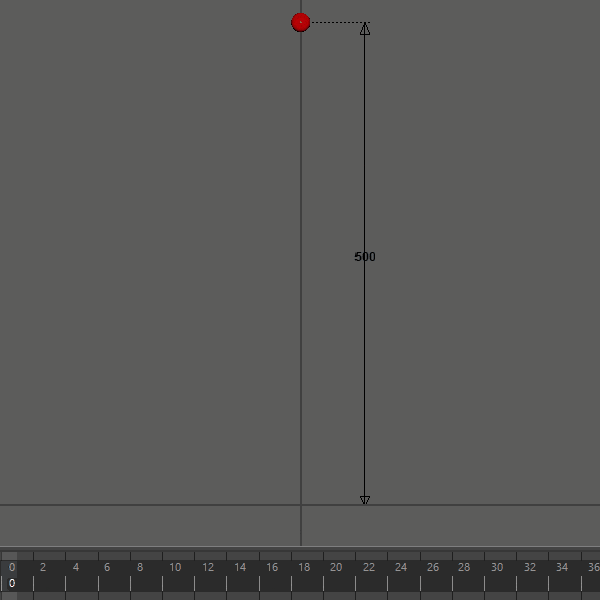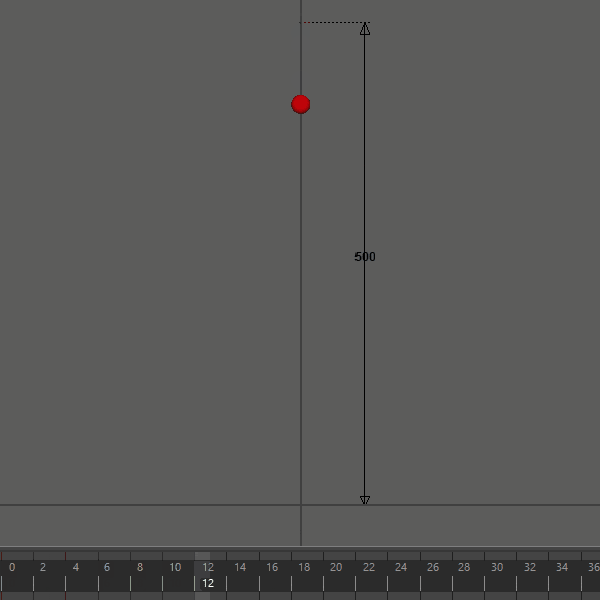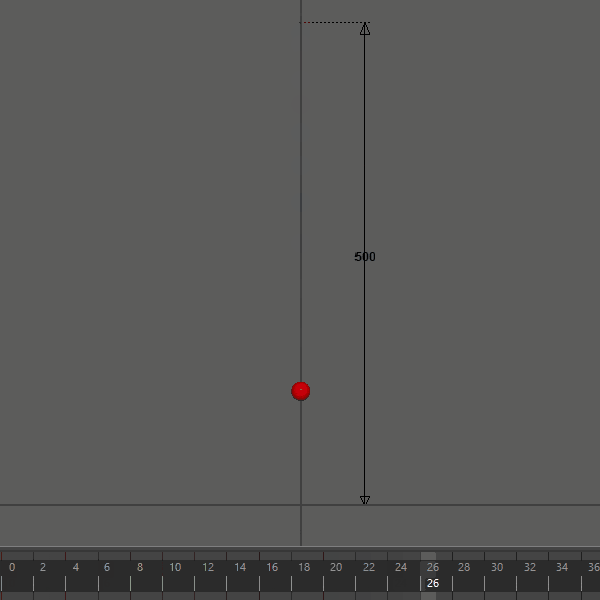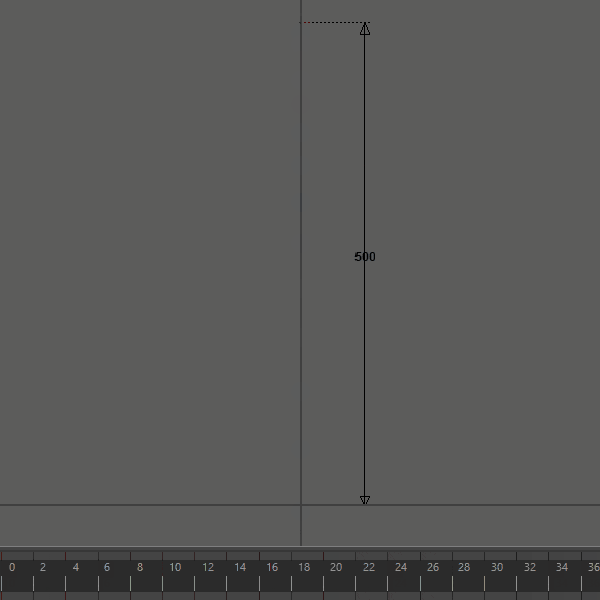
0Fから開始して30F前後の時、つまり約1秒後に地面に到達しました。念のため、物理の教科書に載っていそうな自由落下の公式 $y = \frac{1}{2} g t^2$ で5mの落下にかかる時間を確認してみます。
\begin{aligned}
y &= \frac{1}{2} g t^2 \\
5 &= 4.9 t^2 \\
t^2 &= \frac{5}{4.9} \\
t &= 1.01015 \\
\end{aligned}
だいたいあってそうですね！
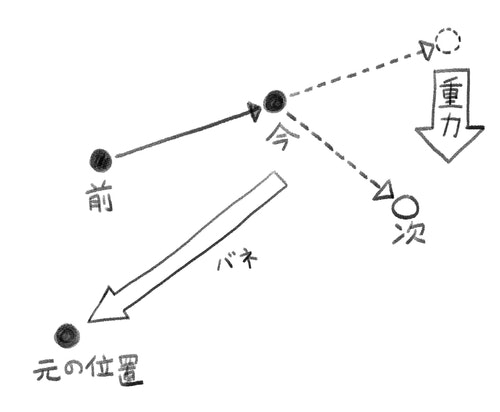
バネ
前項の例では完全にフリーな点を落下させましたが、次は初期位置からバネやゴムのような何かで繋がれているような動きを追加してみます。バネモデルを用いた力は次のように表されます。
F_{spring} = -k \{x(t) - x_0\}
$k$はバネ係数、$x_0$は初期位置です。初期位置から今の位置までのベクトルを$k$倍して反転させるような形になっています。この逆向きの力は初期位置から離れれば離れるほど大きくなります。で、例の式に入れ込むと次のようになります。
x(t + \Delta t) = x(t) + v(t) \Delta t + (g + \frac{F_{spring}}{m}) \Delta t^2
これをBifrostグラフに足してみます。バネ係数$k$はelasticity、質量$m$はmassというパラメータにします。先ほどの重力も含めForceという括りでまとめ直しています。
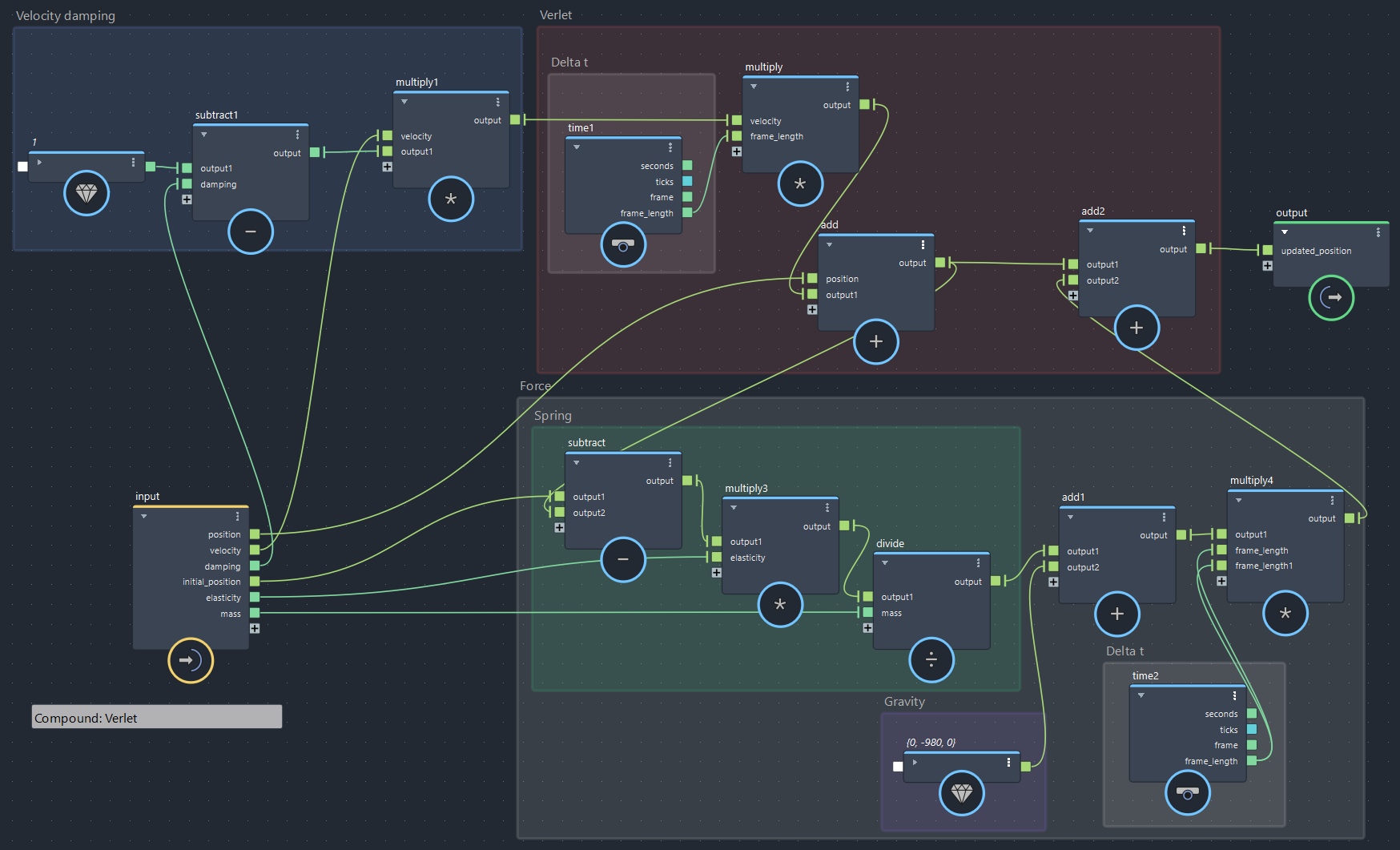
▲bifrostGraphShape > pbd > Verlet
初速度を0、dampingを0.05、elasticityを30、massを1にして再生してみます。バネっぽい雰囲気が出てきました！
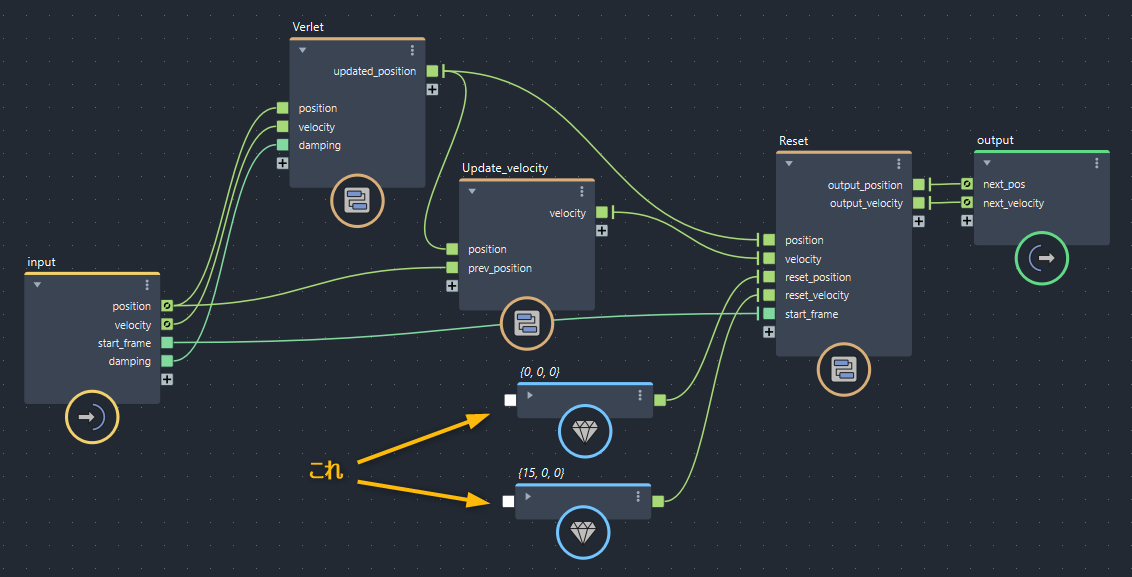
また、いくつかパラメータの組み合わせを変えて試してみました。
左から順に
- damping: 0.05 / elasticity: 20 / mass: 1
- damping: 0.05 / elasticity: 100 / mass: 1
- damping: 0 / elasticity: 30 / mass: 1
- damping: 1 / elasticity: 30 / mass: 1
- damping: 0.05 / elasticity: 30 / mass: 0.1
- damping: 0.05 / elasticity: 30 / mass: 3
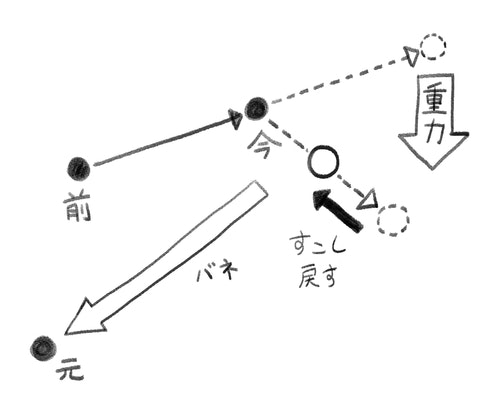
補正前の位置に戻す
ここまでの計算で得られた位置を補正前の位置の方向へｶﾞｯと戻します。ついさっきまで出来るだけ正しそうな重力やバネを表現してたのにお構いなし、強引にやっちゃいます。ﾅﾝﾃｺｯﾀｲ！
具体的には、補正後の位置から補正前の位置へ向かうベクトルを求め、stiffness値でスケーリングしてから補正後の位置に足します。stiffnessは0〜1の値を入力します。1の時には位置の変化が完全に打ち消され微動だにしなくなります。
x(t + \Delta t)' = x(t + \Delta t) + \{x(t) - x(t + \Delta t )\} * stiffness
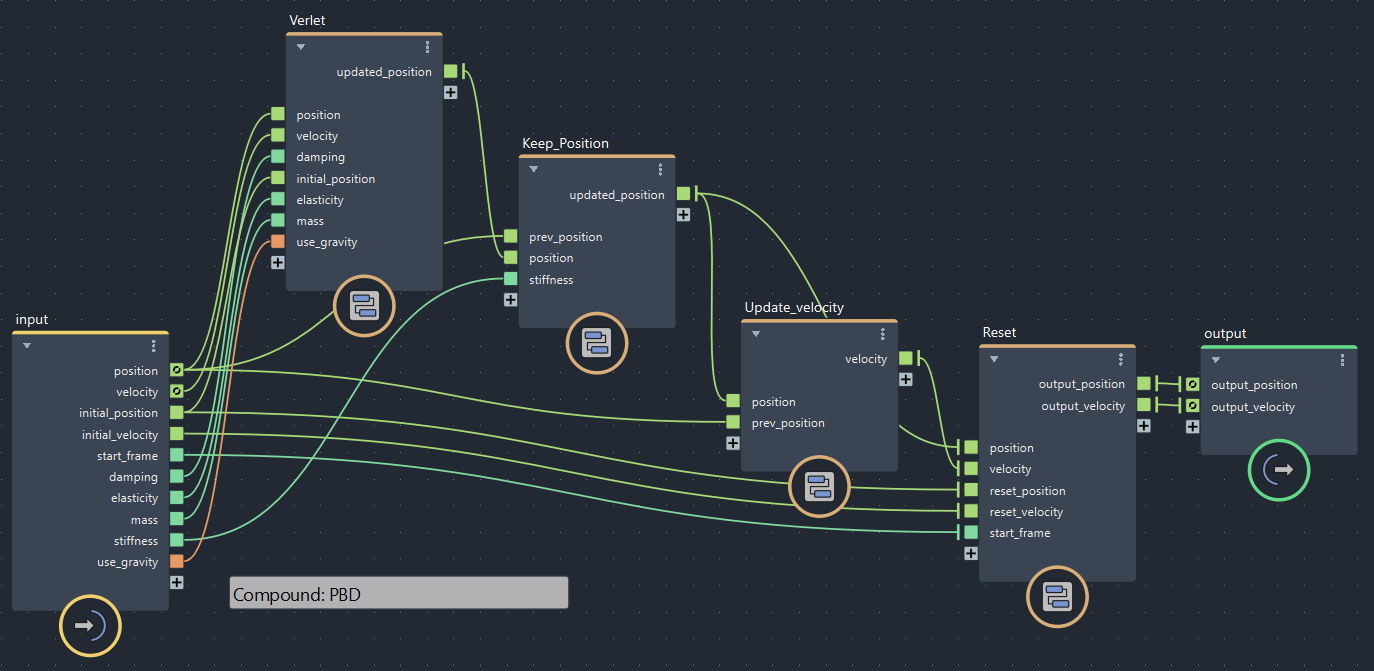
これをBifrostグラフに足してみます。
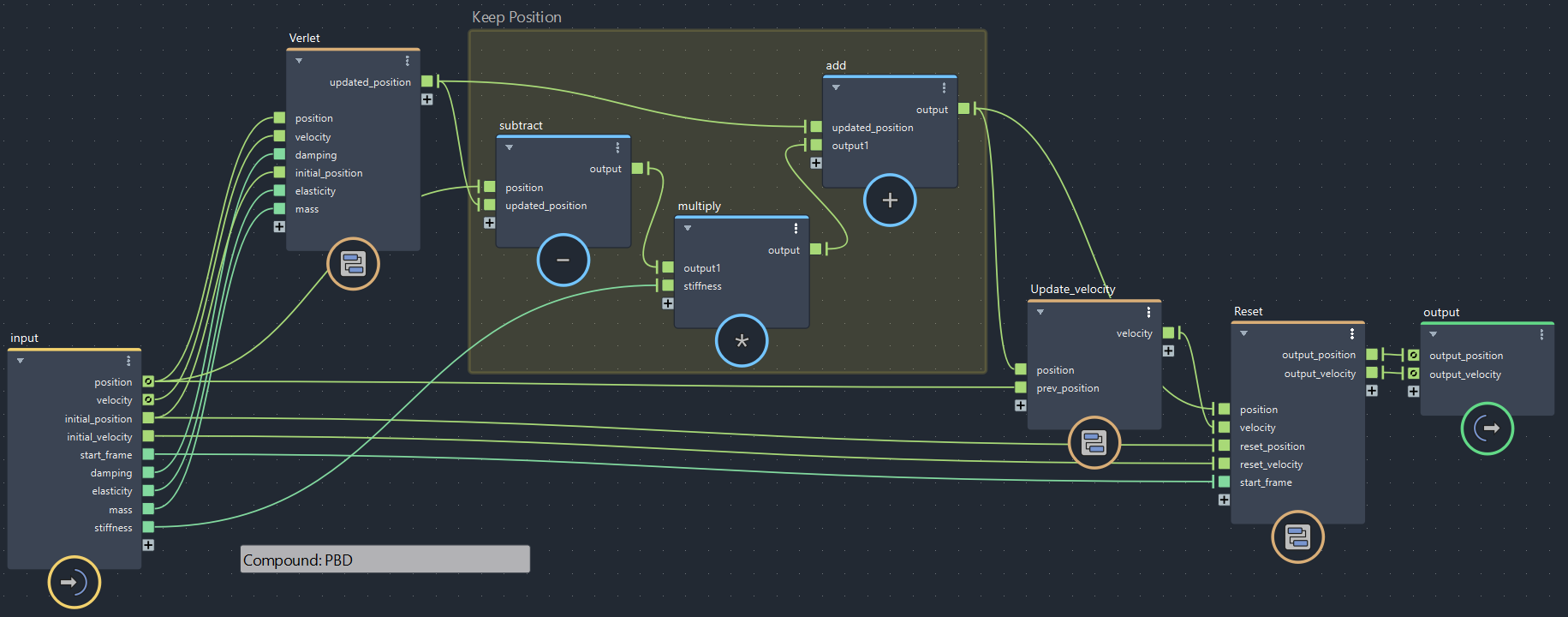
▲bifrostGraphShape > pbd
先ほどと同じく、初速度を0、dampingを0.05、elasticityを30、massを1、そしてstiffnessを0.15にして再生してみます。さっきよりだいぶ動きが鈍くなりました。
第2回でやっとここまで来ました。次回は「制約条件」が加わり位置ベースの良いところが見えてきます。
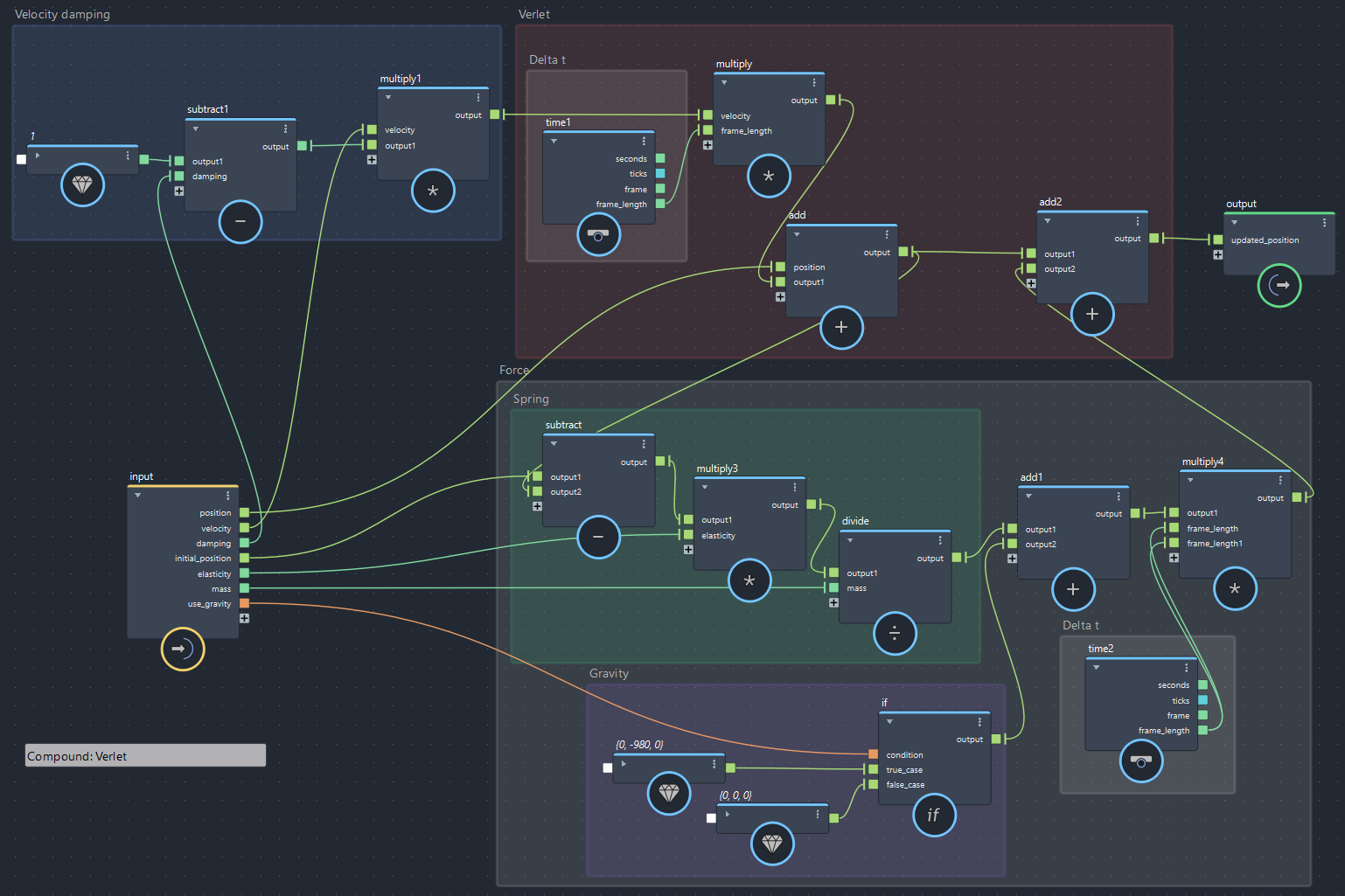
今回のグラフまとめ
bifrostGraphShape
bifrostGraphShape > pbd
重力とバネを加味して次の位置を決定（bifrostGraphShape > pbd > Verlet）
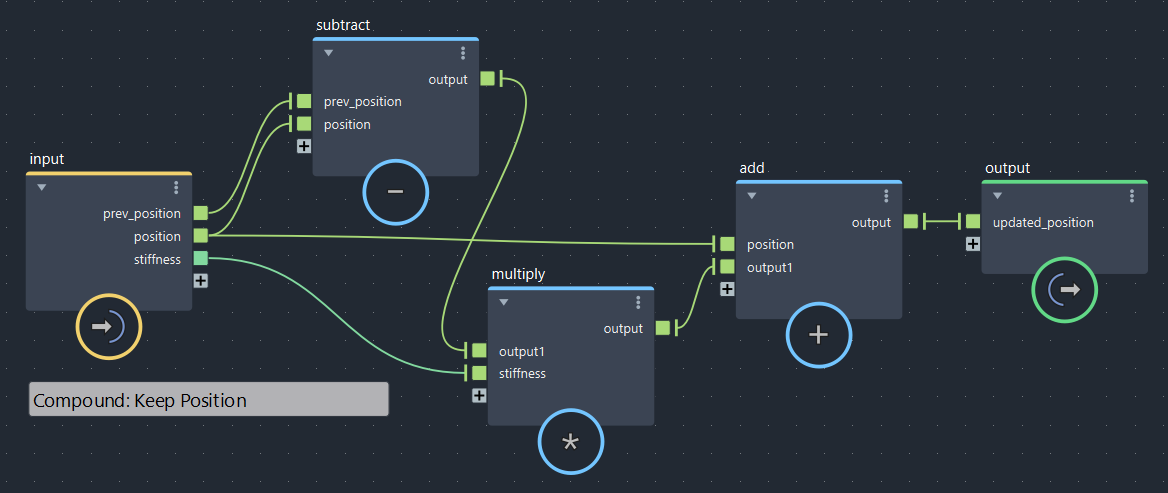
補正前の位置に戻す（bifrostGraphShape > pbd > Keep_position）
前の記事
次の記事