ハイどうもこんにちは!
このシリーズでは、位置ベースの疑似物理シミュや、シンプルなプリミティブのコリジョン検出を利用し、MayaのBifrostでなんやかんや作っていきます。
こんなヤツですね👇
仕組みを理解しようとするとある程度の数学と物理の知識(たぶん高校1〜2年レベル)が必要になりますが、大丈夫です。このシリーズでは一応数式と図を載せはするものの、解説は雑に簡潔に済ませて出来上がったノードグラフをバシバシ載せていきます。
私自身、リグ歴はそこそこ、物理は趣味でかじった程度、Bifrost歴は執筆開始時点で約2週間というニワカっぷりですので、間違いを含む可能性は十分にあります。おかしな点があれば優しく指摘していただけると助かります。
それでは始めます!
使用バージョン
- Maya 2024.2
- Bifrost 2.7.1.1
Bifrostグラフそのものの操作説明からは記載していませんので、完全に初心者であればまず公式チュートリアルなどをご確認ください。
🔗Bifrost ベーシックトレーニング | ムービー | Autodesk :: AREA JAPAN
プラチナゲームズさんのブログもおすすめです。
🔗Bifröst Blög スタート | プラチナゲームズ公式ブログ
位置ベースの物理シミュレーション
これについては先人達のありがた〜い資料を貼った方が良いので、この場での解説は割愛します。
リンクを叩いてすぐそっと閉じた方のために誤解を恐れずに超絶ざっくりまとめると、 『力(Force)を加えると速度(Velocity)が発生し物体の位置(Position)が変化する』 力ベースに対し、『来てほしい場所に直接物体の位置(Position)をいじっちゃおう!』 みたいな手法が位置ベースです。
位置ベースは、高速、暴れにくい、実装が楽、などいろいろとメリットがあります。ただし、近似的な手法であるため正しさを求めるようなものではありません。
前の位置をもとに今の位置を決める
次の式は“ベルレ積分”の式です。「オイオイいきなり積分とか勘弁してくれよ…」という声が聞こえてきた気がしましたが、安心してください。積分と言ってもただの足し算です。
x(t + \Delta t) = 2x(t) - x(t - \Delta t) + \frac{F}{m} \Delta t^2
$t$は今の時間、$\Delta t$は1ステップの経過時間です。$x(t+Δt)$ は次の位置、$x(t)$は今の位置、$x(t-Δt)$は前の位置、最後の$\frac{F}{m} \Delta t^2$は追加で加わる力の部分です。$\frac{F}{m} \Delta t^2$は仮に$F$がゼロだったとしていったん無かったことにしてしまいます。$2x(t)$もバラしちゃいましょう。すると途端に簡単になります。
x(t + \Delta t) = x(t) + \{ x(t) - x(t - \Delta t) \}
ん?日本語おk?
次の位置 = 今の位置 + \{ 今の位置 - 前の位置 \}
はい、「今の位置」に「今の位置と前の位置の差」を足しただけ。
『さっきまでコレくらい動いてたんだから次も同じくらい動くやろ』
です。

ここで3つの時間における位置が出てきましたが、次回計算時には次の位置を今の位置、今の位置を前の位置として1つずらして再利用します。
え?話が長い?そろそろBifrostに行きましょうか…
Bifrostグラフで組むと以下のようになります。“再利用”をBifrostグラフ表現するためには “フィードバックポート” を使います。これがまぁ便利!グラフ右端の出力がグラフ左端の入力として再利用されます。ちなみにフィードバックポートを使うと値が無限に変化し続けてどこかへ行ってしまうので、現在フレームが0以下だったら規定値でリセットするようにしておきます。

▲next_posをcurrent_posに、current_pos_2をprev_posに、Feedbackします

▲Next Posの出力だけ何か適当なオブジェクトのTranslateにつないでおきます
等速直線運動になりましたね!
減速させる
先ほどの式は次のように変形すると速度に相当する値を取り出せます。
\begin{cases}
v(t) = \frac{x(t) - x(t - \Delta t)}{ \Delta t} \\
x(t + \Delta t) = x(t) + v(t) \Delta t +\frac{F}{m} \Delta t^2
\end{cases}
1つ目の式の$v(t)$が速度です。子供の頃に習った気がする【速さ = 距離 ÷ 時間】の形ですね。
また、前の位置$x(t-Δt)$は速度の計算にしか使われていないので、代わりに速度を保存し再利用するよう変更すれば、2つ目の式を使って 『今の位置と速度から次の位置が決まる』 ことになります。前とか今とか次とかややこしかったのが少しスッキリしました。
Bifrostで組むとこのようになります。リセット対象は位置と速度に変わります。$\frac{F}{m} \Delta t^2$は無視したままです。

▲30fpsで先ほどと同じ動きになるよう速度の初期値を15にしてあります。これではまだ減速しません。
速度(velocity)が得られたので、減速させるためvelocity値を雑に下げちゃいます。新たにdamping値を作成し、velocityをスケーリングします。dampingが高いほど速度を抑えたいので次のようにします。dampingは0~1の値を入力します。
v(t)' = v(t) * (1 - damping)
Bifrostグラフは次のようになります。

▲追加したのは左側のVelocity dampingの部分です
dampingを0.05にして再生すると、減速して途中で止まるようになりました。空気抵抗を表現している風に見えますがだいぶ大雑把な計算をしているので雰囲気だけです。

第1回でこれしかできていないので先が長そうですが、しょうがないです!次回は今回スルーした$\frac{F}{m} \Delta t^2$の部分に触れていきます。
今回のグラフまとめ
※それぞれcompoundにまとめています
次の位置を決定(bifrostGraphShape > Verlet)

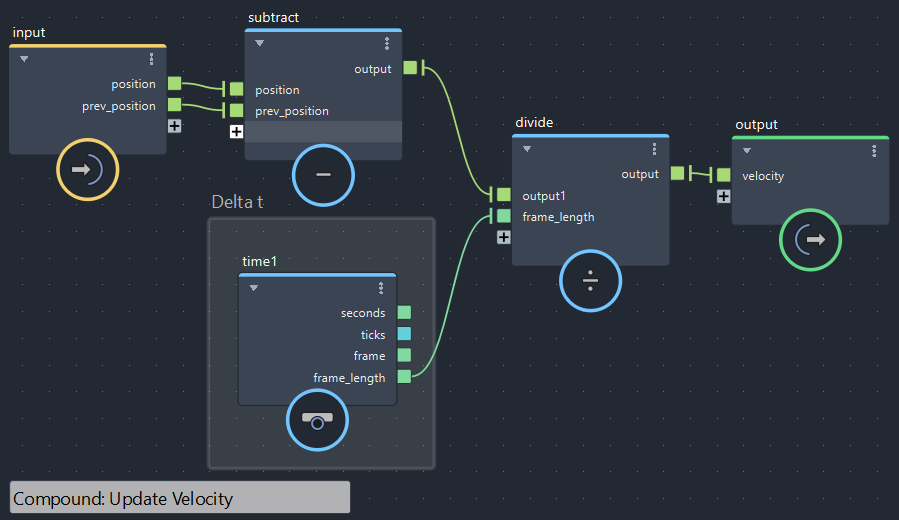
速度の更新(bifrostGraphShape > Update_Velocity)
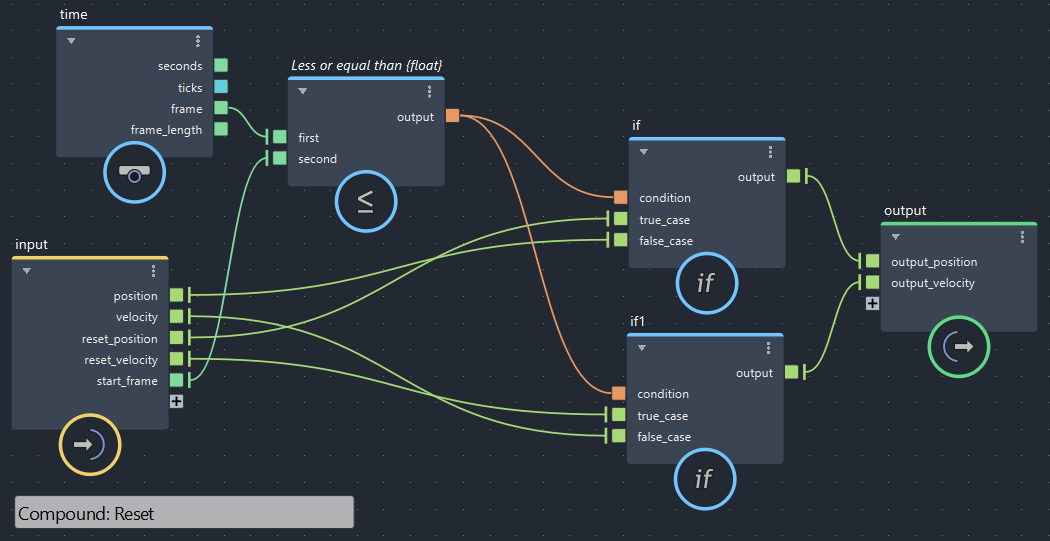
初期値へリセット(bifrostGraphShape > Reset)
次の記事


