ゲーム作りとかCGとかに関わる数学(初歩)①

今回HIKKYさんのアドベントカレンダーに投稿するにあたって、別の温めてたネタはあったんですが諸事情により封印してしまったので、何か別のテーマにしようと考えました。
で、色々考えたのですが、特に思いつかなかったのでCG数学の初歩的な話をしようかなと思います。実際VKetCloudの中でも基本的な数学は必ず使われてますし。

あと「ゲームメーカーズ」さんの記事でも取り上げていただいた、僕のCEDEC+KYUSHU2023の数学のお話がやたらとウケがよかったため、数学の話で行くことにしました。

で最初に書いておくと、書きたかったことの半分もかけていません。 時間の都合上と、あと数式と頭が多すぎるのか、このドキュメントの編集が何度も落ちるからです。
と言うわけで、今回は概要と三角関数とベクトルの話だけにします。

あとは年末年始休みの間にでも続きを書きます。

はじめに

じゃ、どういう話をしていくのかという事なのですが、CEDEC+KYUSHUで話せなかった内容をここで説明していこうかなと思います。

僕は本来VKetCloudのエンジン開発部分担当なので、エンジン内部の色々な所のコードを書いてますし、色々と数学的な知識も利用しています。
とはいえ、あまり難しい話のニーズはないかなと思うので、高校まで数学の話題に絞ってお話をしていこうかなと思います。

大前提

まず、大前提として、プログラマの、とくにゲームプログラマやCGプログラマがやる数学仕事は何かというと「自分で問題を作ってそれを解く」です。

高校まででやってきた「計算する」と言う事はほぼ行いません。もし高校生がこれを見てるんだったら「計算する」はコンピュータに任せて、自分は式を作るのがお仕事だと思ってください。

例えば

sin(45°)=\frac{1}{\sqrt{2}}

ですが、人間がこの計算をすることはないという事です。人間はsin関数に45°(実際にはラジアンでπ/4)を突っ込めばコンピュータがホイホイ計算してくれるわけです。

じゃあ人間は何もせんでいいかと言うと、そんなことはなくて、目の前の問題を数式で表現して、その数式をコンピュータが分かるようにしてあげる事です。

例えば

ax^2+bx+c=0
の解は
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}

と言う事はご存じだと思いますが、左の式から右の式を導出するのがプログラマのお仕事だと思ってください。覚えるんじゃないんです。自分でなんとかして右の式を導き出すのです。

使用する数学の分野(単元？)

で、実際にゲームやCGやVRで使用する数学の分野はだいたいこんな感じです

• 三角関数
  • それぞれの定義
  • 円と三角関数の関係
  • 加法定理
  • 極座標表現
• ベクトル
  • 加算・減算
  • 定数倍
  • ベクトルの大きさ(ベクトルのノルム)
  • ベクトルの正規化(大きさを１にする)
  • 内積
    • を利用してcosθを計算
    • そこから射影を計算
    • それをさらに応用
  • 外積
    • を利用してsinθを計算
    • 法線ベクトルを計算
    • そこからの応用で内外判定
    • 内積との合わせ技で応用
  • 直線の方程式
  • 平面の方程式
    • 直線と平面の交点
  • 基底ベクトル
• 行列
  • 加算・減算
  • 定数倍
  • 行列同士の乗算
  • ベクトルと行列の乗算
  • アフィン変換行列(回転・平行移動)
  • カメラ行列
  • プロジェクション行列
• 数列と合計(Σとかそういうやつ)
• 指数と対数(n乗とかそういう奴)
• 積分(記号の意味と考え方だけ)
• 確率統計(確率と平均と標準偏差くらい)

ちょっと物理

力学と、あと波をちょっとだけやります。

• 力学
  • 重力加速度
  • 坂道ころがり
  • 摩擦ありのとき
  • 打ち上げ(ジャンプ)
    • 最高点(の高さ)
• 波(ホンマに基礎、知識として知っておくくらいの話)
  てな感じです。

それらを応用する分野等

応用編としては

• 曲がるレーザー
• カプセル当たり判定
• 扇形の当たり判定
• 多角形の内外判定
• IKの初歩
• 多関節の実装
• キャラを指定した方向に向ける
• 3Dの当たり判定(特にレイキャスト)
• 初歩的なレイトレーシング
• 古典的レンダリング
• アンビエントオクルージョン

って感じですね。
ゲームとかCGのプログラマはこの辺を全部習得しておく必要がありますね。大変ですけど目指すなら頑張りましょ。

で、ずらずら―ッと書きましたが、こんなん全部説明してたらクリスマス終わっちゃうよォ！！
ということで、ギリギリまで時間の許す限り書いて、もう間に合わなそうなところで打ち切りとします。
CEDILにも以前に話した数学の資料が上がってるので、この記事を読んで気になった人はそれを覗いたり、僕の書籍「DirectX12の魔導書」を買ってください(笑)

はい、じゃあそれでははじまりはじまり～。

三角関数

じゃあまず、三角関数をやってくれるかな？
ベクトルとどっちを先にしようか迷う所さんですが、ベクトルの内積と三角関数のcosが関わってるので、先に三角関数やったほうがいいかなと思います。

三角関数自体は昔は主に測量に利用されていたのではないかと思われます。元をたどれば紀元前2千年くらいだとか。歴史あるッスね。
https://en.wikipedia.org/wiki/History_of_trigonometry

定義

で、定義は以下の通りです。
高校の頃だと

\displaylines{
sinθ=\frac{高さ}{斜辺}\\
cosθ=\frac{底辺}{斜辺}\\
tanθ=\frac{高さ}{底辺}
}

みたいに覚えたかもしれませんが、ゲームやCGに応用するのが目的ならば、以下のこの図で覚えてください。

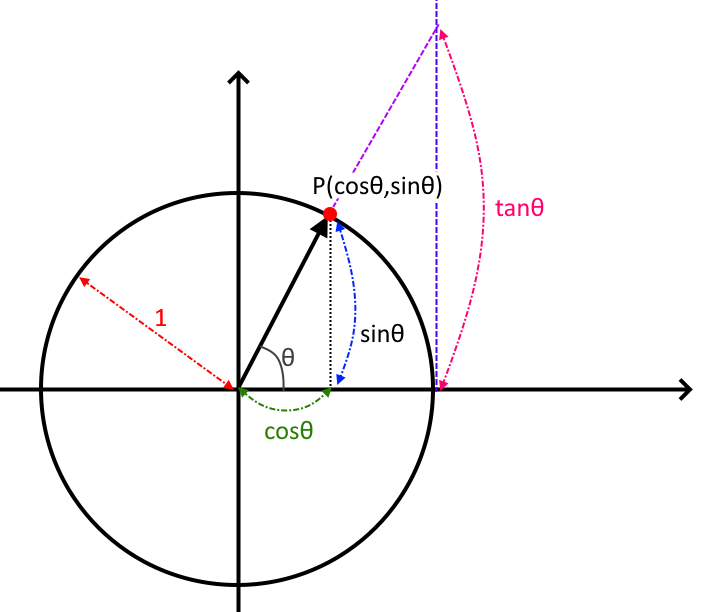
半径１の円周上の特定の点Pを打ち、原点からそこまで線を引き、それとX軸とのなす角度をθとしたとき
X=cosθ
Y=sinθ
となります。cosが横！sinが縦！くらいの認識でいいんで覚えておいてください。
点P(cosθ,sinθ)とかでもいいです。

ではtanθは何を表すのかと言うと、Ｘ軸と円の交点から真っすぐ上に補助線(接線)を伸ばして、それが原点Oから点Ｐを結ぶ線の延長線上と交わる点までの高さなんですね。

確かにtanはtangentの略ですし、英語のtangible(触る事の出来る)との関連性を考えると、この「接線」から生まれたものと考えられますね。

別にどっちで考えてもいいのですが、ゲームやＣＧではこの「円」を頭に入れておいたほうが後々使えますよ、と。

そして角度θを少しずつ変えていくことによって、波みたいな形になるのが三角関数です。

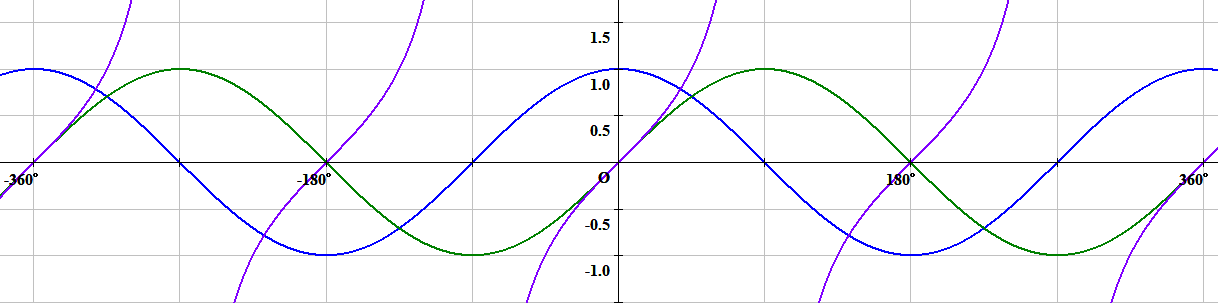
この「波」になる特性を利用されたりもします。

で、この三角関数というのは見ての通り角度が必要なのですが、3DCGで使う時に「角度を測る」というのが意外と面倒くさく、3Dの場合はベクトルと併用してもうちょっと扱いやすくします。

ごくごく当たり前の性質

定義からすると、ごくごく当たり前の性質ですが、押さえておいて欲しい性質があります。まずは

cos^2θ+sin^2θ=1

です。これはθがどんな角度でも成り立ちます。何故かというと、そもそもsinとcosの定義が半径1の円周上の点における原点からのX距離とY距離なので、ピタゴラスの定理が成り立ち、必ず１になります。

次にこれも当たり前のことですが、$tanθ=\frac{高さ}{底辺}$でしたが、この底辺と高さはcosθとsinθそのまま当てはまりますので、

tanθ=\frac{sinθ}{cosθ}

です。

加法定理

いや、別に加法定理なんか知らなくてもいいのよ？例えば

sin(75°)=\frac{\sqrt{6}+\sqrt{2}}{4}

なんてなーsinに75°ぶっこめば答えを返してくれるんだからさ。でもそうじゃないんだ。重要なのは「なんでそうなのか」を知っておくことなのよね。例えばこういう風な２つの直角三角形について考えてみましょう。

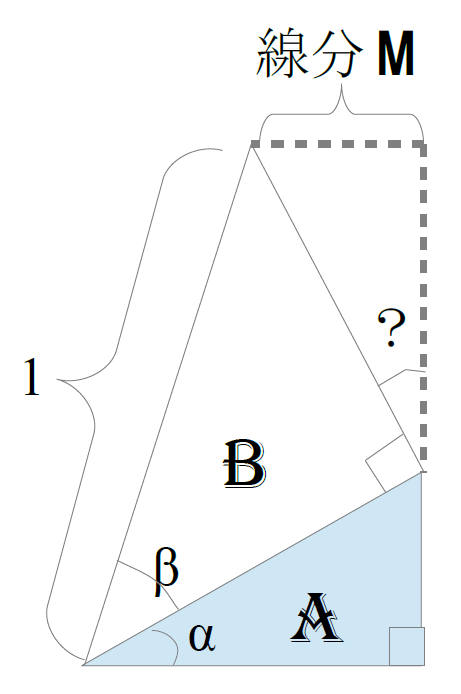
この図においてsin(α+β)を求めたいとします。斜辺が１なので、三角形Bのてっぺんまでの高さを返せばいい事は分かりますね？

わかる所から片付けていきましょう。まず三角形AはBの底辺を斜辺とした直角三角形です。三角形Bの底辺は三角関数の定義よりcosβですね？これがAの斜辺なわけですから、三角形Aの高さはcosβsinαです。

そして残りの高さですが、これは三角形Bの右上に補助線を引いててっぺんまでの直角三角形を作ります。
そこで、図における？の部分の角度ですが、これは何になるでしょうか？αでしょうかβでしょうか？

これは見ての通り、直角三角形Aのαじゃない方の角度は90-αですよね？で、三角形Bの直角部分が間に入っている。
つまり90-α+90+?=180が成り立つわけですね？左辺右辺の180°が打ち消されるので-α+?=0つまり?=αで、右上の直角三角形は直角三角形Aと相似の関係にあるわけです。
そうなると角度が分かっているわけですから、斜辺が分かれば残りの高さが求まります。

右上の直角三角形の斜辺は直角三角形Bの高さにあたるので、sinβなわけです。これを斜辺とすると、残りの高さは直角三角形の底辺に当たるため、sinβcosα

これと最初に求めたcosβsinαを足せばいいので
sin(α+β)=sinαcosβ+sinβcosα

一応これは全部こんな感じで自分で導出できますが、とりあえずそれは読者にお任せするとして
sin(α+β)=sinαcosβ+sinβcosα
cos(α+β)=cosαcosβ-sinαsinβ
sin(α-β)=sinαcosβ-sinβcosα
cos(α-β)=cosαcosβ+sinαsinα
となるわけです。これが加法定理です。

余弦定理

これ実はInverseKinematicsみたいな動きの時にも応用できるので、知っておいたほうがいい。思いっきり測量に使えそうな定理。
たいそうな名前がついてますが、ごくごく当たり前の話です。sinとかcosは直角三角形のための者ではありますが、ちょっと応用すると任意の三角形に役立てる事が出来ます。

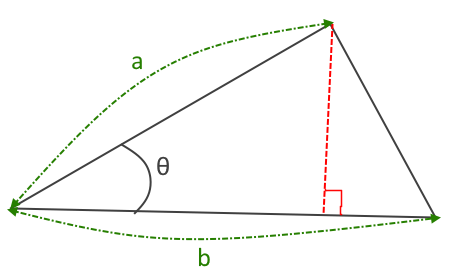
図のように、三角形の２辺の長さと、その間の角度が分かっている状況で、残りの辺の長さが測れない状況があるとします。例えば測量などでAとBはメジャーで測れるけど、河や岩などの障害物があるせいでAとBの間の距離が測れない、そんなときに使えるものです。

図のように直角三角形ができるように補助線を引きます。そうすると当然補助線の長さはasinθですよね？
で、補助線の左側を△Aとし、補助線の右側を△Bとして考えます。そうするとどちらも直角三角形ですね。

となると△Aの底辺はacosθになり、△Bの底辺はb-acosθになります。
これで直角三角形△Bの底辺と高さ(△Aと共有)が求まりました。ということはあとはピタゴラスの定理より大元の三角形の残りの辺が求められるわけです。仮にそれをcとすると

c^2=(asinθ)^2+(b-acosθ)^2=a^2sin^2θ+b^2-2abcosθ+a^2cos^2θ

ここで、$cos^2θ+sin^2θ=1$なので

\displaylines{
c^2=a^2sin^2θ+b^2-2abcosθ+a^2cos^2θ\\
c^2=a^2sin^2θ+a^2cos^2θ+b^2-2abcosθ\\
c^2=a^2(sin^2θ+cos^2θ)+b^2-2abcosθ\\
c^2=a^2+b^2-2abcosθ
}

となります。これを余弦定理と言います。ゲームやCGでこれを応用しようとすると、例えば初歩的なInverseKinematicsを腕周りに実装したいとします。

で、まず肩の座標Pは分かってる、拳の座標Qも分っているとします。でも肘の位置がわからない。
で、当然ですが人間の前腕と上腕は伸び縮みしませんのでこれも定数s,tとします。

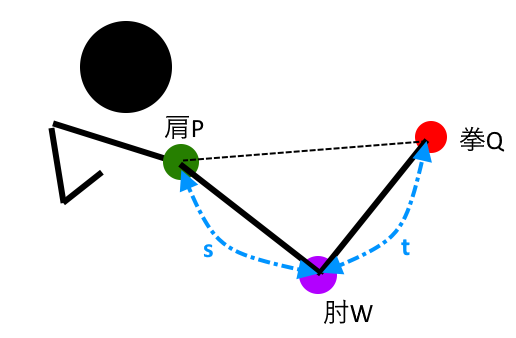
P→Qの距離はピタゴラスの定理で求まりますので、これを|PQ|としておきます。

はい、そこで持ち出してくるのが先ほどの$c^2=a^2+b^2-2abcosθ$です。今回の場合、肘の位置は分かりませんが、全ての辺の長さが分かっています。となるとあとは分からないのはこの三角形の角度ですね。具体的にはPQに対するPWの角度です。

つまりまずは上式をcosθの式にしてしまいます。

\displaylines{
2abcosθ=c^2-a^2-b^2\\
cosθ=\frac{c^2-a^2-b^2}{2ab}
}

となります。あとはプログラムの数学関数acosというのがあって、これはcosθの値からθを求めるもので
θ=acos(cosθ)
というわけです。なんかおかしな式に見えますが、角度が分かる前にcosθが求まってしまっているのでこうなるわけです。
ゲームやCGでは、角度が分かっている事の方が稀で(3Dは角度が測りづらい)、このため先にcosθの値自体が求まる事が多々あります。
覚えておきましょう(この話、あとからまた出てきます)

極座標表現

所謂(x,y)や(x,y,z)で座標の位置を表現するのを「直交座標表現」と言います。直交するXYもしくはXYZ軸を用いて場所を表すからですね。

これに対して、「原点からの距離」「基準となる軸からの角度」で表現するのが「極座標表現」です。
円で三角関数を定義する時に見たと思いますが、原点からの距離が1なら半径が1なわけで、そうするとX軸からの角度がわかるだけでその座標は求まるわけです。
もし原点からの距離がrならば、先ほどの円の半径もrになるだけなので、これも後は角度が求まれば座標を特定できるわけです。
このように、「原点からの距離」と「基準軸(この場合X軸)からの角度」で座標を表現することを「極座標表現」と言います。

例えば点Pが原点からr、X軸からの角度がθだとした場合点P(r,θ)と書けるわけです。
で、この極座標を直交座標に直すのも簡単で、その場合、半径rがそのまま三角形の斜辺に当たるわけですから、
点Pは直交座標に直すとP(rcosθ,rsinθ)になるわけです。

ちなみに三次元の時はP(r,θ,Φ)のように、原点からの距離と２つの角度によってあらわせます。

はい、極座標はただ単に座標の表現方法についての話でしたが何故三角関数として取り扱ったかと言うと、極座標→直交座標の変換をやっておきたかったからです。

とりあえず三角関数についてはこの辺で終わりにしましょう

ベクトル(これが一番大事だと思います)

ここで言うベクトル自体は非常に簡単で、x,yもしくはx,y,zの組を一緒くたに扱うためのものだと思ってもらっていいと思います。プログラムで書くと

struct Vector2{
    float x,y;
};
struct Vector3{
    float x,y,z;
};

これだけの話です。ね？簡単でしょ？で、この3つの成分を使って座標を表したり変位(移動した距離と方向)を表したり、速度(速さと方向)を表したりします。

ベクトルの加減算

で、この一緒くたに扱う時には+や-も定義されますが、これもそれぞれの成分どうしを計算すればいいだけです。つまり(2dだけ書きますが)

struct Vector2{
    float x,y;
    Vector2 operator+(const Vector2& vec){
        return {x+vec.x , y+vec.y};
    }
};

と言うわけです。簡単ですよね？説明が前後しますが加算減算に関してはそれぞれの成分を混ぜずに加減算するだけです。$\vec{A}=(x_a,y_a) , \vec{B}=(x_b,y_b)$とおいて数式で書くと

\displaylines{
\vec{A}+\vec{B}=(x_a + x_b , y_a+y_b)\\
\vec{A}-\vec{B}=(x_a - x_b , y_a-y_b)
}

というわけですね。3Dで$\vec{A}=(x_a,y_a,z_a) , \vec{B}=(x_b,y_b,z_b)$とおいて数式で書くと

\displaylines{
\vec{A}+\vec{B}=(x_a + x_b , y_a+y_b, z_a + z_b)\\
\vec{A}-\vec{B}=(x_a - x_b , y_a-y_b, z_a - z_b)
}

となるわけで、結局のところ、成分を混ぜずに分けて計算すればいいわけです。

定数倍

定数倍も簡単で、それぞれの成分すべてにその定数をかけてやればいい

\displaylines{
n\vec{A}=(nx_a , ny_a, nz_a)
}

加減算と合わせ技すると

\displaylines{
n\vec{A}+m\vec{B}=(nx_a + mx_b , ny_a+my_b, nz_a + mz_b)\\
n\vec{A}-m\vec{B}=(nx_a - mx_b , ny_a-my_b, nz_a - mz_b)
}

となるし、もちろん分配法則も成り立つので

\displaylines{
n(\vec{A}+\vec{B})=n\vec{A}+n\vec{B}=(nx_a + nx_b , ny_a+ny_b, nz_a + nz_b)\\
n(\vec{A}-\vec{B})=n\vec{A}-n\vec{B}=(nx_a - nx_b , ny_a-ny_b, nz_a - nz_b)
}

とはいえ、いちいちこんなもん分解しない。式を解いていくときはベクトルはベクトルのまま式を展開していったほうが楽なので、ベクトル形式は最後の最後まで分解しない方がいいでしょう。
最終的にX,Y,Zそれぞれの成分が欲しくなった時にそれぞれの値を見るようにしましょう。

ベクトルの大きさ(ベクトルのノルム)

ちょっとノルムって聞いたことがないかもしれませんが、これはベクトルを矢印で表したときの、その矢印の長さだと思っていていいでしょう。記号としては縦棒|を2つ重ねて$||\vec{A}||$のように表現します。まぁ、面倒な場合は絶対値記号$|\vec{A}|$でも意味は通じるかなと思います。

で、最初にベクトル自体はX方向Y方向Z方向の値を持っている話をしましたが、これはもちろんそれぞれ直交しています。となるとあとは 三平方の定理(ピタゴラスの定理) を使用すればよくて

\displaylines{
2Dのとき\|\vec{A}\|=\sqrt{x_a^2+y_a^2}\\
3Dのとき\|\vec{A}\|=\sqrt{x_a^2+y_a^2+z_a^2}
}

となります。

ベクトルの正規化(normalize)

座標平面や座標空間におけるベクトルと言うのは「大きさ」と「方向」を持った矢印としてあらわされますが、方向だけが欲しくて、大きさが邪魔な時があります。例えば自機狙い弾を作ろうとして点Aから点Bに向かうベクトルを作ろうとすると

\overrightarrow{AB}=\vec{B}-\vec{A}

となりますが、このベクトル$\vec{AB}$をAから発車しようとして$\vec{A}$に足してしまうと

\vec{A}+\overrightarrow{AB}=\vec{A}+\vec{B}-\vec{A}=\vec{B}

となってしまい、自機狙い弾が一瞬で目標に当たってしまいます。そんな弾避けれるわけないじゃん！というわけで、速度をそろえる必要があります。その時に大きさが邪魔なので大きさを１にしたいわけです。
この「大きさを１にする」事をベクトルの正規化と言います。やり方は簡単で、ベクトル自体をベクトルの大きさで割ればそりゃベクトルの大きさが1になるわけです。

正規化済みのベクトルは$\hat{A}$みたいに頭に^を付けて表現したりします。
そうすると

\hat{A}=\frac{\vec{A}}{\|\vec{A}\|}=\frac{(x_a,y_a,z_a)}{\sqrt{x_a^2+y_a^2+z_a^2}}

なわけです。
この正規化、滅茶苦茶頻繁に使うので覚えておきましょう。

内積

これはベクトル特有の計算ですね。計算の仕方は簡単で、それぞれの成分どうしを乗算して、そしてその乗算した成分を全部足す。これだけです。
内積の記号はドット・を使います。

\displaylines{
2Dの場合　\vec{A} \cdot \vec{B}=x_a x_b + y_a y_b\\
3Dの場合　\vec{A} \cdot \vec{B}=x_a x_b + y_a y_b + z_az_b\\
}

です。簡単でしょ？計算自体は小学生でもできそうです。
実はこいつには強力な性質があるのです。

\vec{A} \cdot \vec{B}=\|\vec{A}\| \|\vec{B}\|cosθ

これですね。2Dのときも3Dの時も同様です。もちろん目を付けるのはcosθです。両辺をAの大きさBの大きさで割ればいいですね。

cosθ=\frac{\vec{A} \cdot \vec{B}}{\|\vec{A}\| \|\vec{B}\|}

ここで得られるcosθはかなり有用 です。得られるのはこれだけではありません。AからBに垂線を下したときの射影の長さが得られます。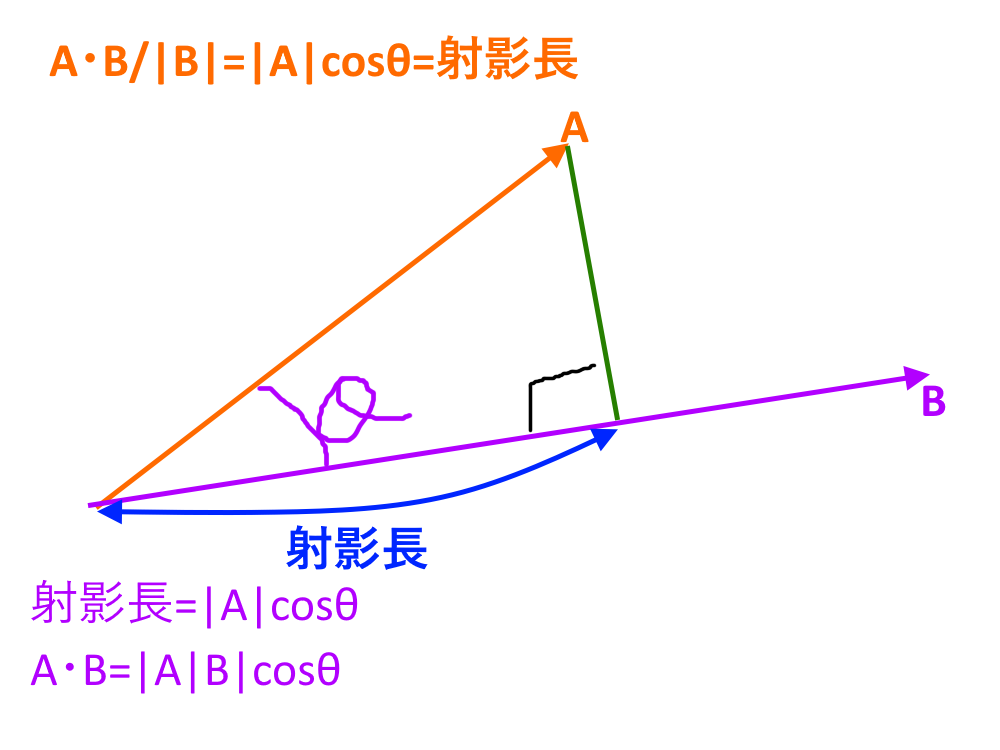
計算としては、垂線を下すわけですからそこは直角三角形になります。そうなると射影長は直角三角形の底辺に当たるわけで。そうなると射影長＝底辺＝$|A|cosθ$になるわけですが、この$|A|cosθ$は内積の性質の時に出てきた式の両辺を|B|で割ってやればいいので

射影長=\|\vec{A}\|cosθ=\frac{\vec{A}\cdot\vec{B}}{\|\vec{B}\|}

となります。
この 「射影長」もクッソ使います ので、ここで覚えておきましょう。

外積(定義だけ)

ちょっとアドカレ的に時間がないので外積に関しては定義だけ書いておきます。
こいつの計算法は「互い違いにかけて引く」そして、「外積の結果は2つのベクトルに直交するベクトルになる」 です。
外積の記号は×を使います。

\vec{A}\times\vec{B}=(y_az_b-y_bz_a , z_ax_b-z_bx_a , x_ay_b-x_by_a)

と言った感じです。2Dの場合はZ軸がないため直交することができず結果的にスカラー値となります。

\vec{A}\times\vec{B}=x_ay_b-x_by_a

ちなみに、この直交するベクトルの大きさはsinθと関わっていて

\|\vec{A}\times\vec{B}\|=|\|\vec{A}\|\|\vec{B}\|sinθ|

になります。あ、あと一つ重要な性質として、外積の順序が変わると符号が反転します。つまり

\vec{A}\times\vec{B}=-\vec{B}\times\vec{A}

です。

応用としては3Dにおいて法線ベクトルを求めたり、領域の内外判定に使ったりしますが、時間ないので別の機会に回します。

直線の方程式(3D)

高校だと

\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}

とかって習うかもしれませんが、あたしアレ嫌いなのよね。なんか直感的に直線って分かりづらいし。
ということで、ベクトルと「媒介変数t」を用います。この媒介変数と言うのは「任意の実数」です。つまり実数なら何でもいい。ゴチャゴチャ言うよりみてもらったほうがいいでしょう。
まず方向を表すベクトルを$\vec{V}$とします。で、確実に通る点を$P_0$とします。そして直線上の点をPとします。で、先ほども言ったようにtは任意の実数とします。すると

P=P_0+\vec{V}t

となります。シンプルでしょ？tは任意の実数なので、もうなんでもいいからこの世のすべての実数tをぶわーっとあてはめます。するとあら不思議、一直線上に点が並んでまるで一つの直線のように見えるではありませんか。

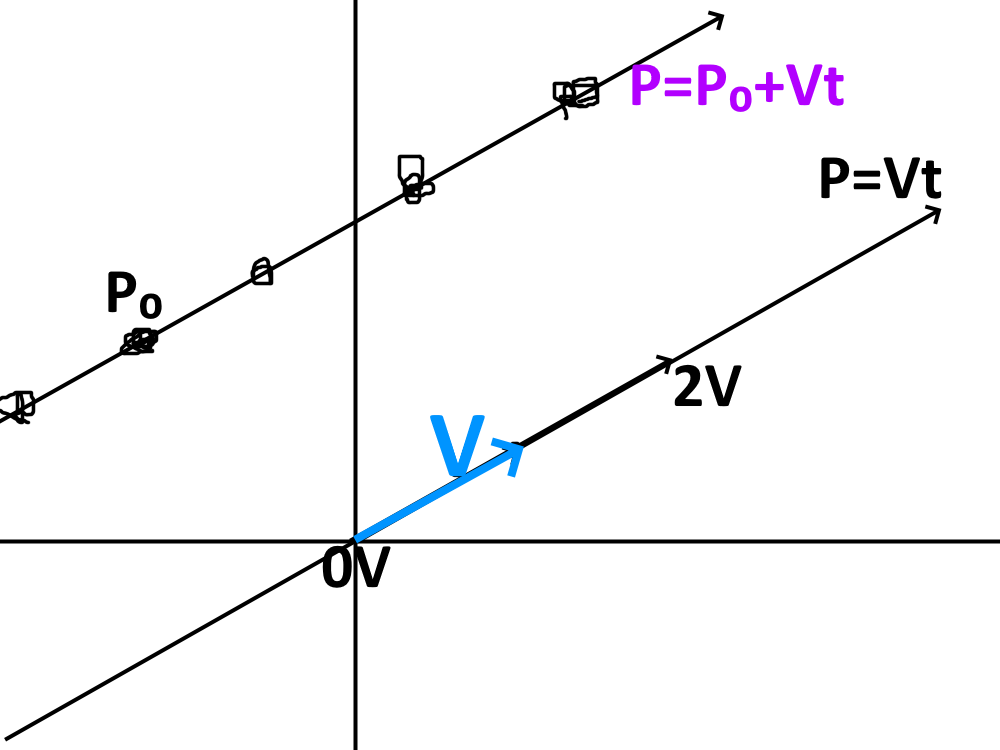
なお、$P_0$は「どこでもいいから確実に通る点」と言いましたが、これがないとt=0の時に必ず原点を通る事になってしまい、原点から離れられないからです。2D直線の時の切片みたいなもんですね。

先にも書きましたが、ベクトルに関することはいちいち分解せずにまとめて表記したほうが扱いやすいというのも、こっちの書き方の直線の方がいい理由ですね。

平面の方程式

はい、平面の方程式ですが、これも高校だと

ax+by+cz+d=0

なんて習いますが、これまた「あたしこの表記嫌いなのよね」です。
これもまた直感で分かりづらい。んじゃねえかなと。一応x,y,zは平面上の点の座標でa,b,cは法線ベクトルで、$\frac{-d}{\sqrt{a^2+b^2+c^2}}$が原点からのオフセットと言う説明がつきますが、分かりづれえんだー！！！
と言うわけで、ぼくのかんがえたさいきょうの定義 はこうです。

\vec{P}\cdot\vec{N}=d

う～ん、シンプル。
美しい！！え？これが平面の方程式？何言うてんの？って思われるかもしれませんが、説明します。

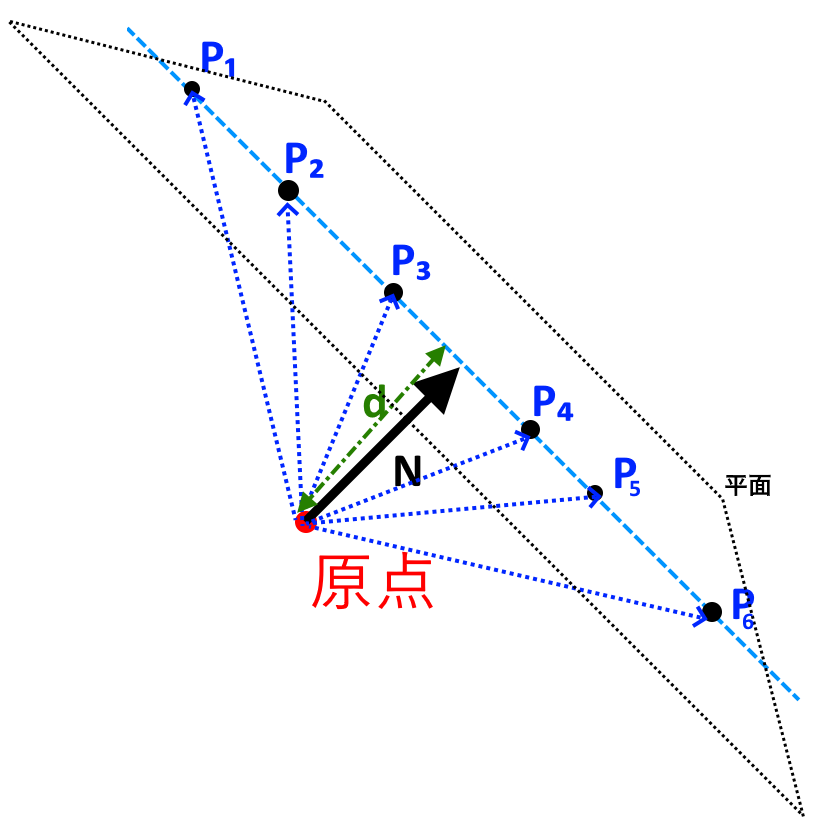
分かりづらい図かもしれませんが、任意の点Pの座標を原点からのベクトル$\vec{P}$として扱い、それと法線ベクトル$\vec{N}$都の内積をとります。Nが正規化されていればPとNの内積は「射影長」になります。

\displaylines{
射影長=\frac{\vec{P}\cdot\vec{N}}{\|\vec{N}\|}=\vec{P}\cdot\hat{N}
}

任意の点から法線方向への射影長を計算しているわけですが、ということは先ほどの平面の方程式は

\vec{P}\cdot\vec{N}=d

ですが、dが定数なので、点Pが法線方向に対して射影長が常に一定の任意の点を表しているわけです。

つまりそれを満たす任意の点Pをぶわーっと集めると平面になるというわけです。
ちなみにこれ展開すると点P(x,y,z)とN(a,b,c)の内積なわけですから
ax+by+cz=d
になるわけで、高校の頃のと同じ式がすぐ出てきます。dの位置がちょっと違うだけですね。
というか、ax+by+cz+d=0の定義だと、dを増やせば増やすほど法線と逆方向にオフセットするから、混乱の元なのよね…あーやだやだ

直線と平面の交点

はい、ここでベクトルの考え方がまた強力に作用します。高校的な解き方なんてやってらんねーYO！って話です。
すでに直線と平面の方程式を定義したわけですが、レイトレーシングなどを行う際にこの交点を求めたかったりします。どうしましょうか？
まずベクトル表記のまま並べてみます。

\displaylines{
P=P_0+\vec{V}t\\
P\cdot\vec{N}=d
}

これを両方満たす点Pが直線と平面の交点です。
これ、連立方程式にできますよね？ここで変数は点Pと媒介変数tだけで、あとはすべて定数です。
さらに言うと、tが求まれば直線の方程式から自動的に点Pが求まるので、ともかくtを求めればいい。
と言う事になります。じゃあ、連立させていきますが、交点では当然両方の式の点Pを満たすのでこう書けますね？

(P_0+\vec{V}t)\cdot\vec{N}=d

内積も分配法則が成り立ちますので、

\displaylines{
P_0\cdot\vec{N}+\vec{V}t\cdot\vec{N}=d\\
\vec{V}\cdot\vec{N}t=d-P_0\cdot\vec{N}\\
t=\frac{d-P_0\cdot\vec{N}}{\vec{V}\cdot\vec{N}}
}

でtが求まります。あとは最初の直線の方程式にこれをブッ込めば平面との交点を求める事ができます。

P=P_0+\vec{V}(\frac{d-P_0\cdot\vec{N}}{\vec{V}\cdot\vec{N}})

基底ベクトル(Basis Vector)

基底ベクトルというか、元になるベクトルについて考えてみようってのがこの話です。
例えばベクトル$\vec{V}$がありますが、これはx,yだったり、x,y,zの構成要素からできていますね？
このそれぞれの成分の構成要素もベクトルとして扱いましょうと言う事です。
どういうことかと言うと2Dの場合の基底ベクトルはそれぞれ

\displaylines{
    \vec{X}=(1,0)\\
    \vec{Y}=(0,1)
}

と書けるわけです。この$\vec{X} , \vec{Y}$これが基底ベクトルです。
この基底ベクトルは、ひとまず大きさは一定とします。つまり長さが１(正規化済み)としておきます。

で、例えばベクトルVのX成分、Y成分を抽出したいなら、内積を使えばいいわけです。
仮に$\vec{V}=(a,b)$だとすると

\displaylines{
    \vec{V}\cdot\vec{X}=a\\
    \vec{V}\cdot\vec{Y}=b
}

と、まぁ、ごくごく当たり前の結果が得られるわけです。
逆に言うと座標やベクトルとは

\displaylines{
P=x\vec{X}+y\vec{Y}\\
\vec{V}=a\vec{X}+b\vec{Y}
}

と言えるわけです。はい、この定義に納得してもらったうえで基底ベクトル$\vec{X},\vec{Y}$を加工したとします。
分かりやすい加工の例で言うと、両方ともn倍してみる。と

\displaylines{
    \vec{X'}=(n,0)\\
    \vec{Y'}=(0,n)
}

基底ベクトルがこうなってしまうと$a\vec{X}+b\vec{Y}$の結果は(na,nb)となってしまい、拡大したのと同じことになっています。もちろん均等拡大縮小だけじゃなくて横長にしたりもできますね。

\displaylines{
    \vec{X'}=(m,0)\\
    \vec{Y'}=(0,n)\\
    \vec{V}=a\vec{X'}+b\vec{Y'}=(ma,nb)
}

はい、今度は大きさは１のままで「任意の方向」を向かせてみましょう。実はこれが本題です。
結果だけ言うと「回転」になるのですが、回転の場合は「角度」が必要になりますが、3Dで角度を用いるのは実は難しい場合があります。
しかし基底ベクトルの考え方を使うと「任意の方向」を向かせることができるようになります。

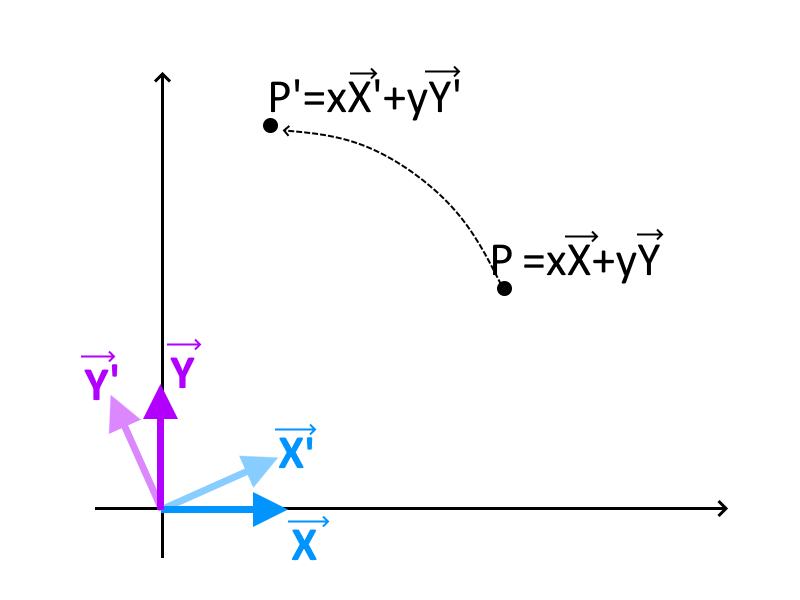
先にも書いたように、「角度を求めなくてもいい」は3Dにおいては(場合によっては2Dにおいても)強いアドバンテージになるので、この考え方は頭に入れておきましょう。

続編記事へのリンク