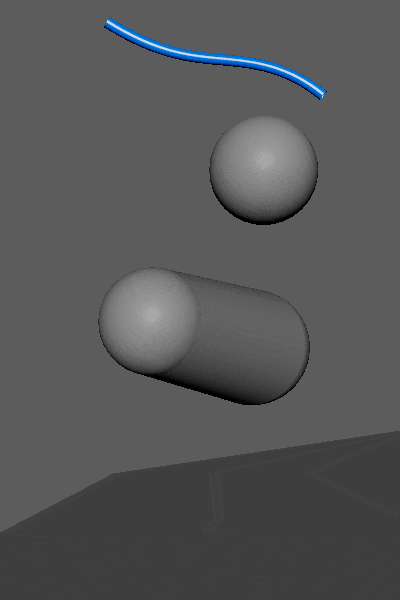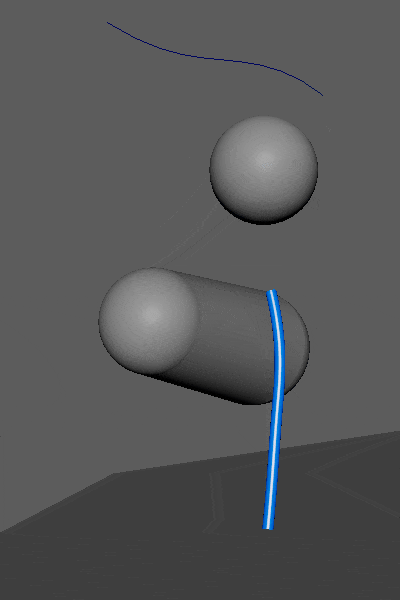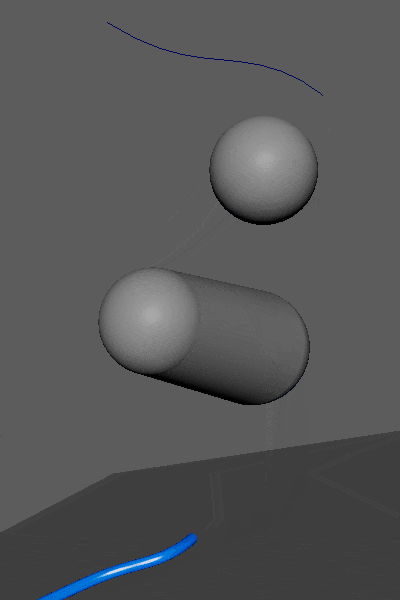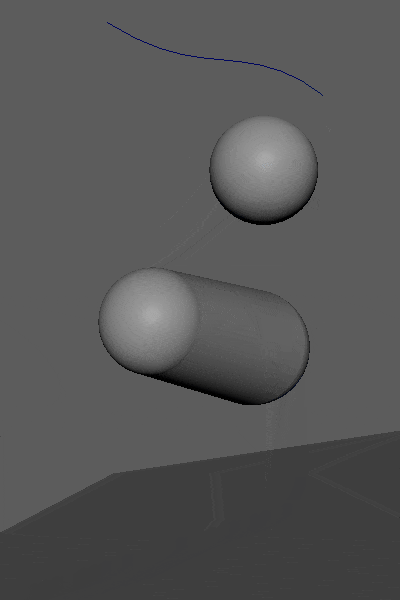ハイどうもこんにちは！
前回までずっと1つの点$p$と向き合ってきたのでだいぶ絵的に地味な回が続いてしまいました。すこーしだけ反省しています。ただ、大事な要素は網羅できたと思うので、ここから複数の点をまとめて動かしたいと思います。ようやくジョイントチェーンとか、ポリゴンとか、カーブとかを扱えます。
それでは始めます。
ジョイントチェーン
ベースのBifrostグラフはもう前回で出来ています。第3回の「片方が固定の距離制約」が入ったものに対し「コリジョンによる補正」を加えたものですね。球、カプセル、地面が入ったパターンでいきます。
やることは単純、bifrostGraphShapeを丸ごと複製して連ねていくだけなのですが、その前に少し小細工が必要になります。1階層目の補正済み位置を元にjointの回転へ反映させた後で、2階層目の計算に移らないといけません。 なのでBifrostグラフ内で回転の計算まで済ませてしまいます。
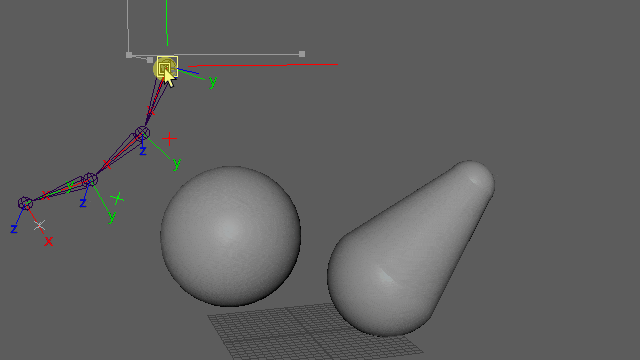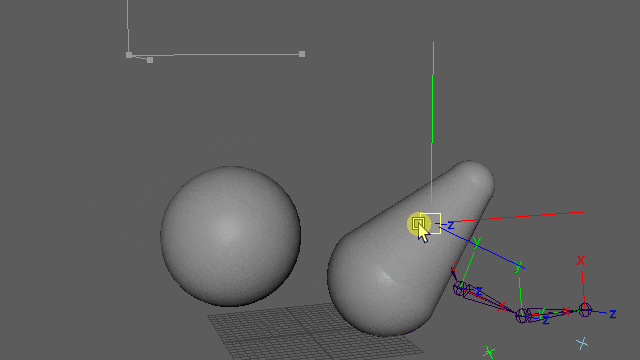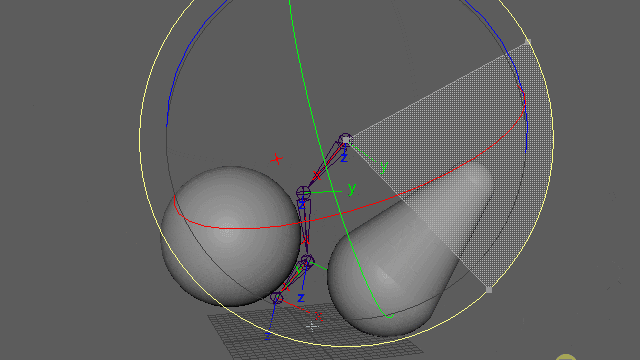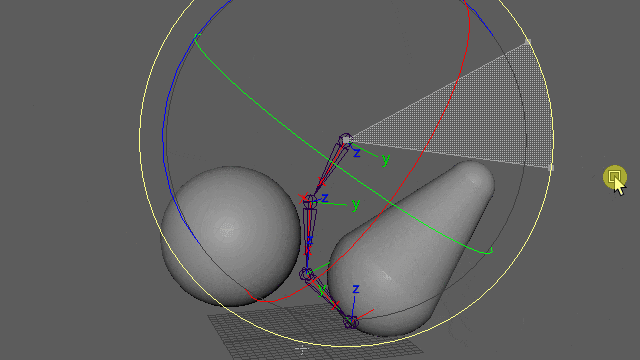
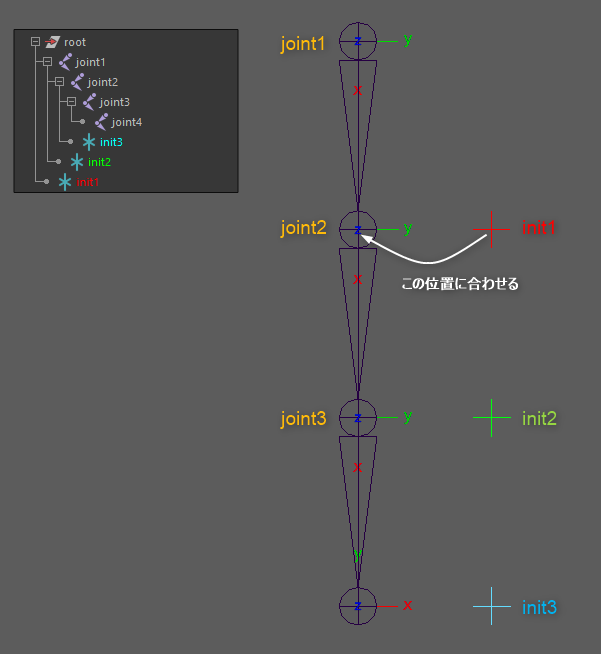
まず、jointチェーンとlocatorを以下のように準備します。見やすいように右によけていますが実際にはlocatorはjoint位置にスナップしてある状態です。root空間でjoint1の制御を、joint1空間でjoint2の制御を、、、と上流から順に処理していくための階層構造です。
Bifrostグラフに回転の計算を追加します。出力はただの位置（ベクトル）ですので、補正前後の2つのベクトルにおいて間の回転角を計算すれば良さそうです。が、jointはJoint Orientを含めた元トランスフォームを考慮しないといけないので、Joint OrientとParent Inverse Matrixを受け取っておきます。
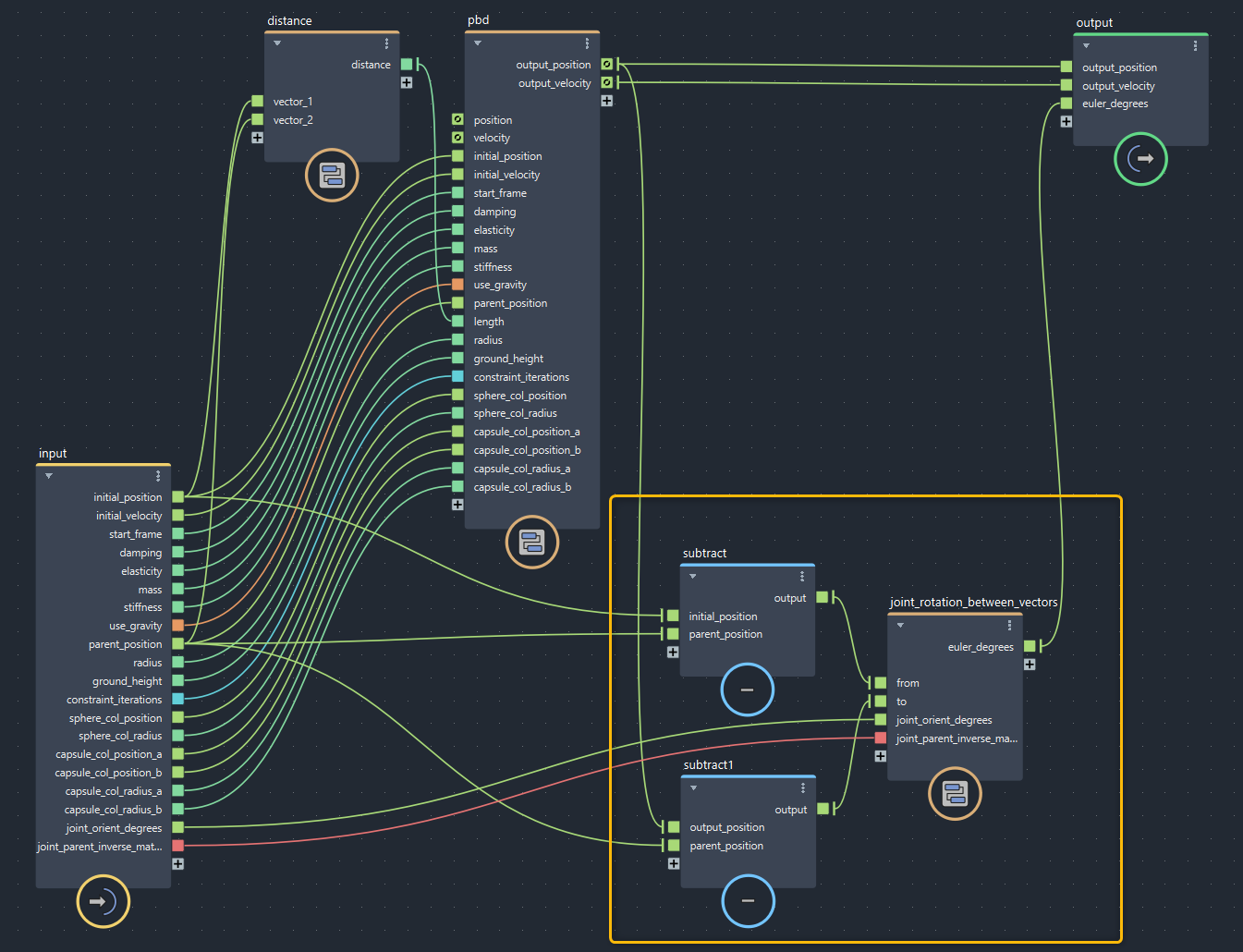
▲bifrostGraphShape（黄色枠が追加した箇所です）
ベクトルからjointの回転を得るコンパウンドjoint_rotation_between_vectorsは以下のようになっています。前後はほぼ radians⇔degrees や euler⇔quaternion などの変換です。中央付近、JointOrient（のinverse）とParentInverseMatrixで2つのベクトルを逆トランスフォームしてから既存のノードrotation_between_vectorsで回転を取得しています。
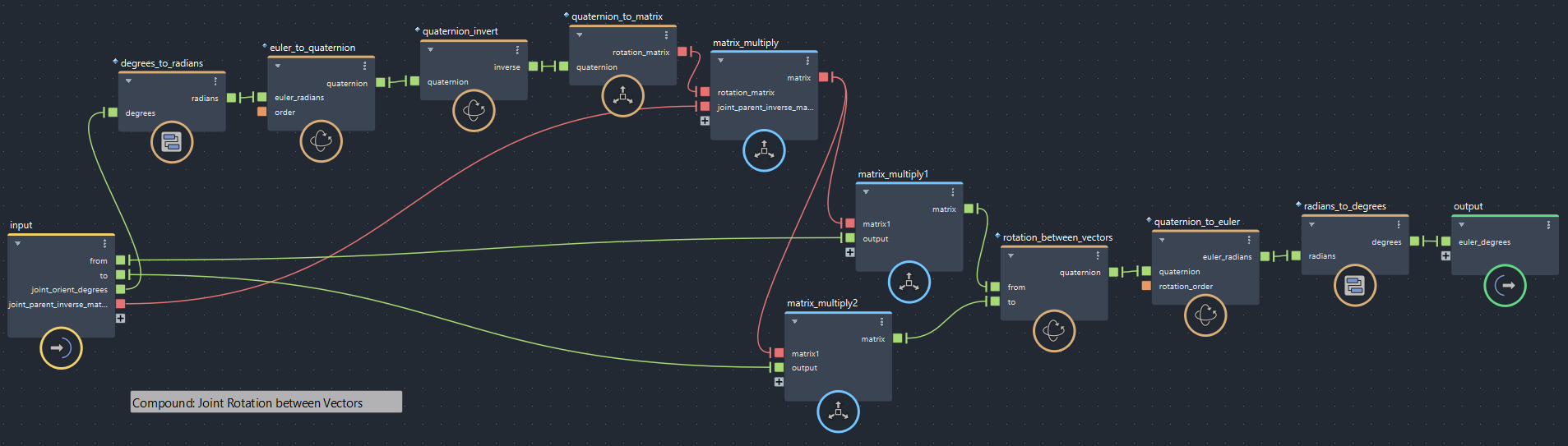
▲bifrostGraphShape > joint_rotation_between_vectors
Maya側のノード接続はこんな感じです。parent_positionにはjointのワールド位置を直接使いますが、WorldMatrixから得るとCycleの警告が出てしまうのでParentMatirxとTranslateを合わせたもので代用します。VectorProductのOperationは「Point Matrix Product」です。
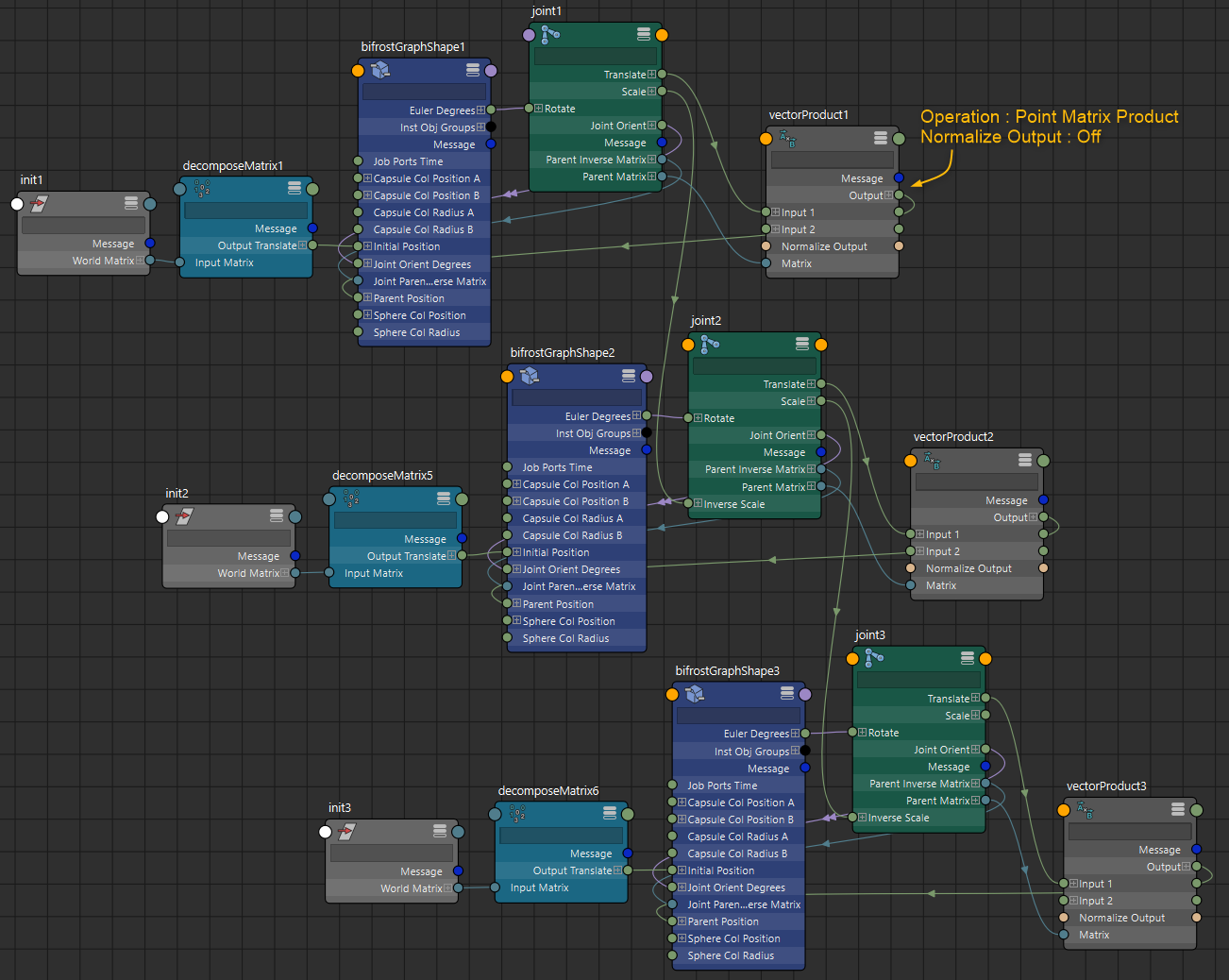
ちょっとややこしい構造になってしまったかと思いますが、要はアップベクトル不要のエイムコンストレイントをBifrostグラフに内包したような状態です。
メッシュ
メッシュの頂点数ぶんグラフを複製するわけにはいかないので、Bifrostの便利機能“オートループ”を使います。今までの「位置$x$を入力し$x’$を受け取るコンパウンド」は、位置配列$( x_1, x_2, x_3, ... x_n)$ を入力し同じく配列で受け取ることもできます。ポートの型をAutoに変更し、あとは繋ぐだけです。
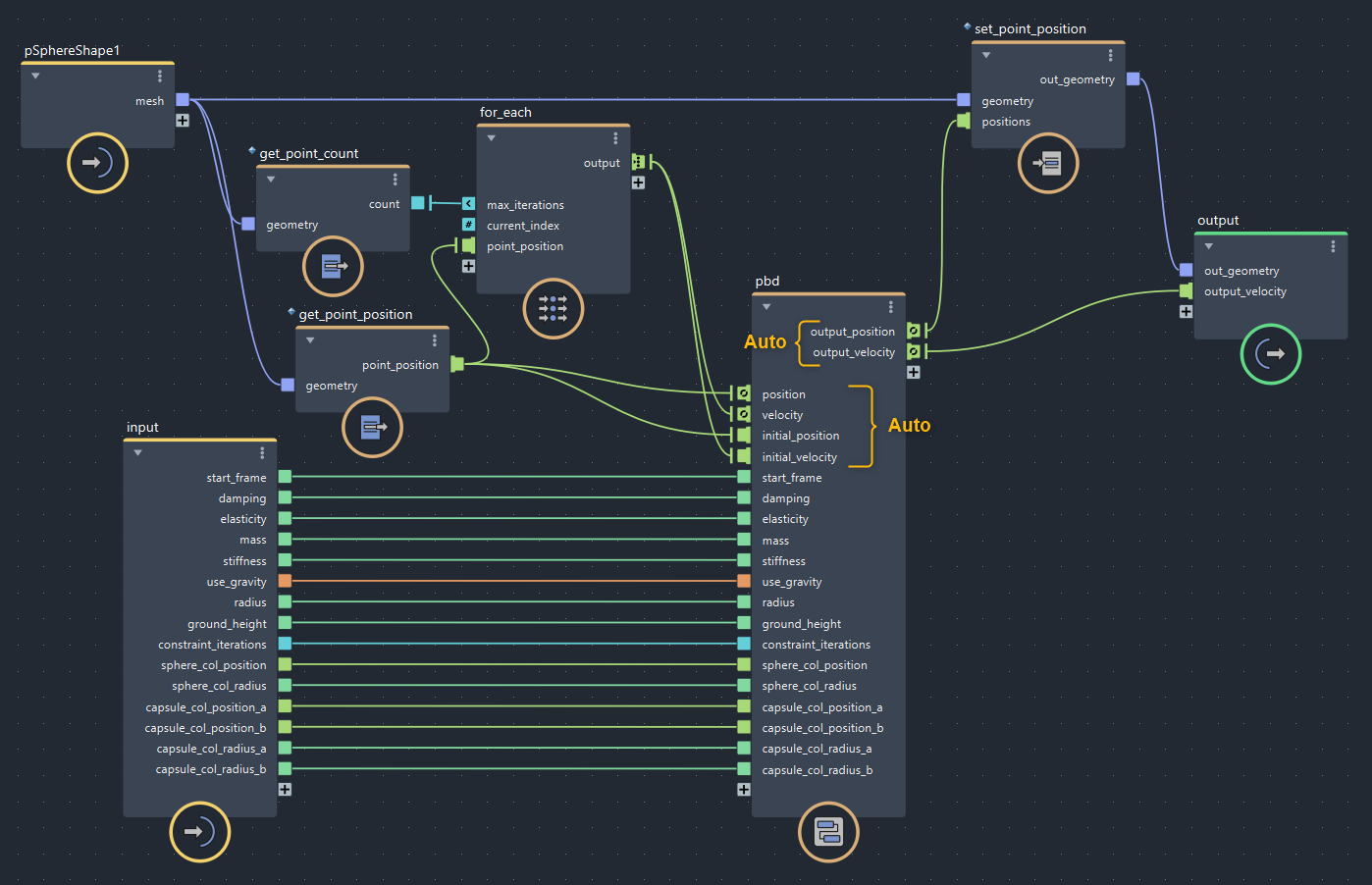
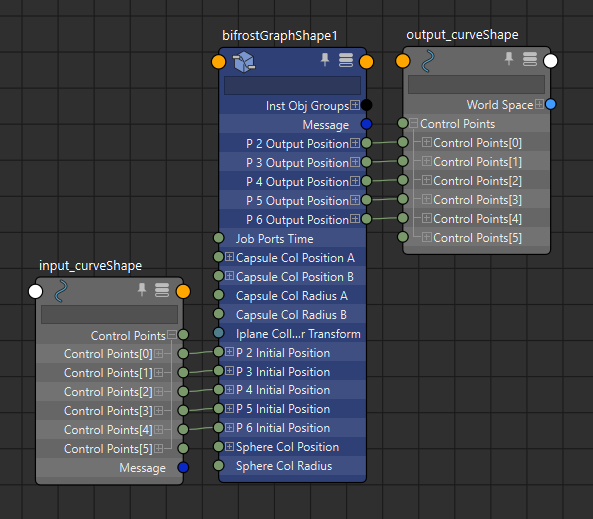
Bifrostグラフは次のようになります。前回の「コリジョンによる補正」が入ったもの から 「距離制約」だけ取り除いたものをベースに、pbdコンパウンドへ位置配列を繋げています。ポリゴンの場合はgeometryを入力としてget_point_positionで頂点位置の配列を得られます。配列をgeometryに戻す場合はset_point_positionです。
▲bifrostGraphShape
速度配列は位置配列と同じサイズで全要素(0,0,0)にしたいのでfor_eachを使用してこのように組みました。グラフが途中で途切れてるのがなんか気持ち悪いですが、まぁいいでしょう…
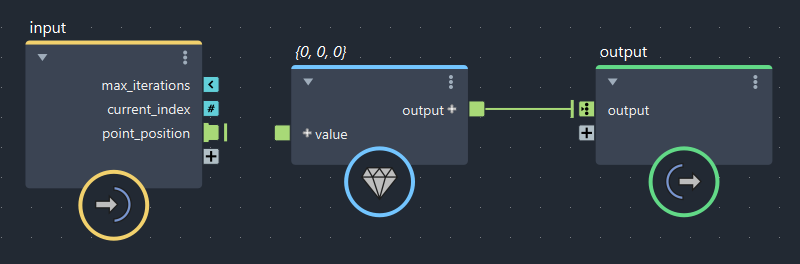
▲bifrostGraphShape > for_each
iterateのポートも忘れずにAutoにしておきます。
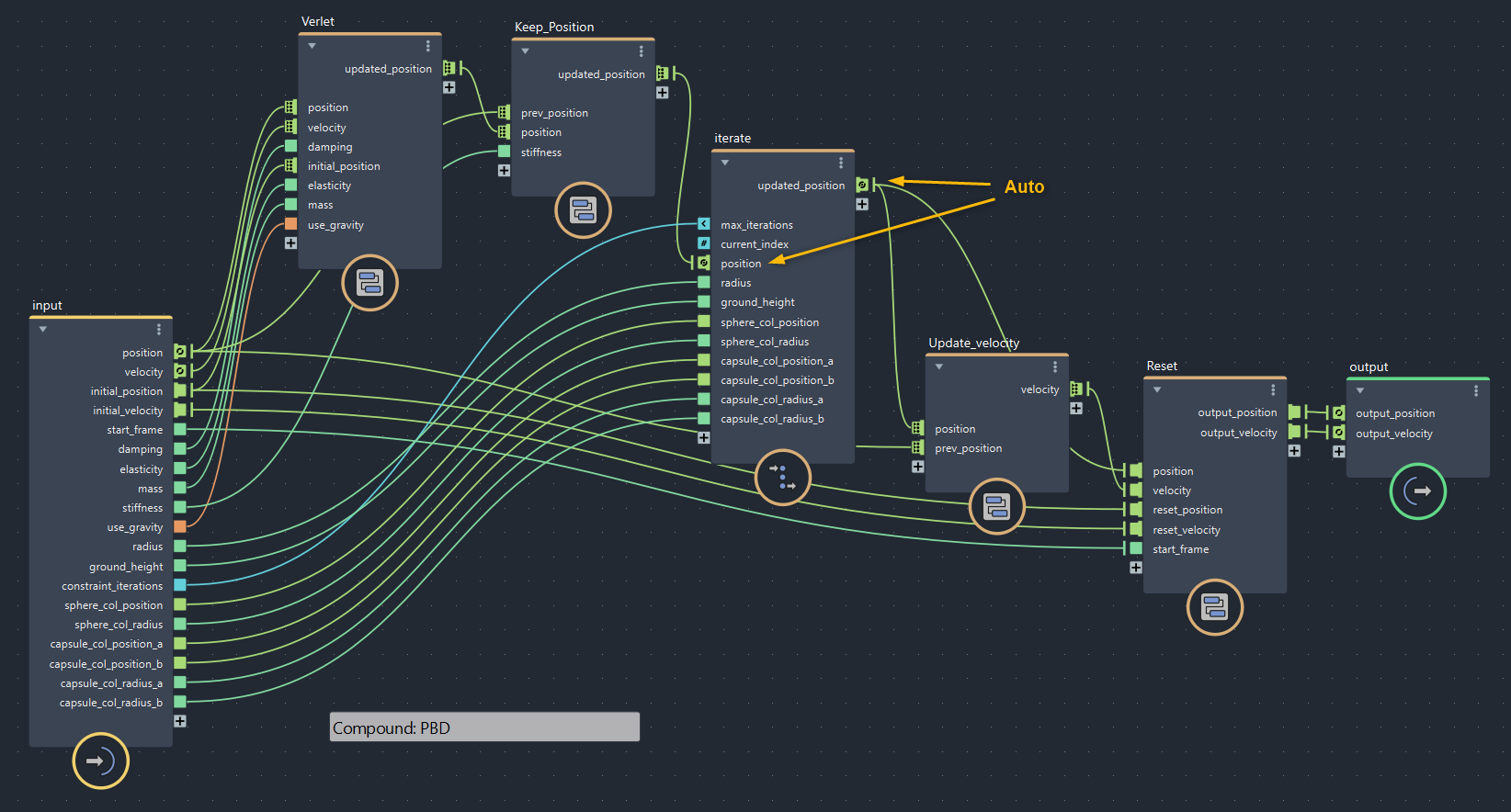
▲bifrostGraphShape > pbd
動かしてみると、このようになりました。
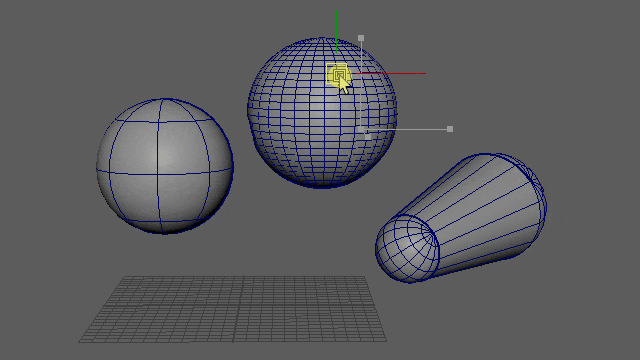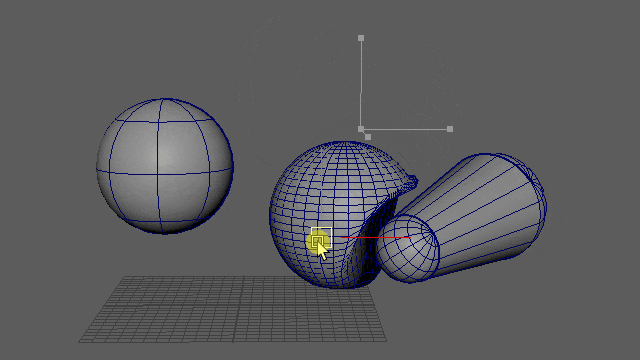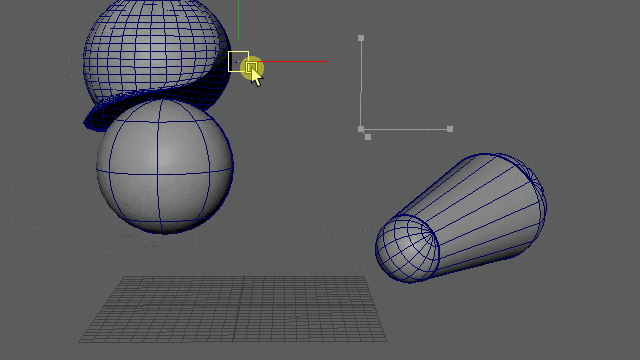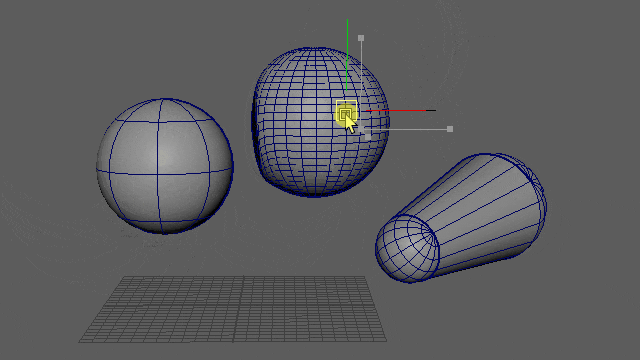
▲※重力はオフにしてます
動いてはいるんですが、面白みに欠けますね…。もっとこう、ソフトボディ感が欲しいです。
頂点カラーで重み付け
ということで、よく動く場所とあまり動かない場所を頂点カラーで塗り分けたパターンをやってみます。
頂点カラーをBifrostで取得するにはget_geo_propertyを使って「colorSet1」を指定します。得られるのは同じく配列なのでオートループの対象になります。
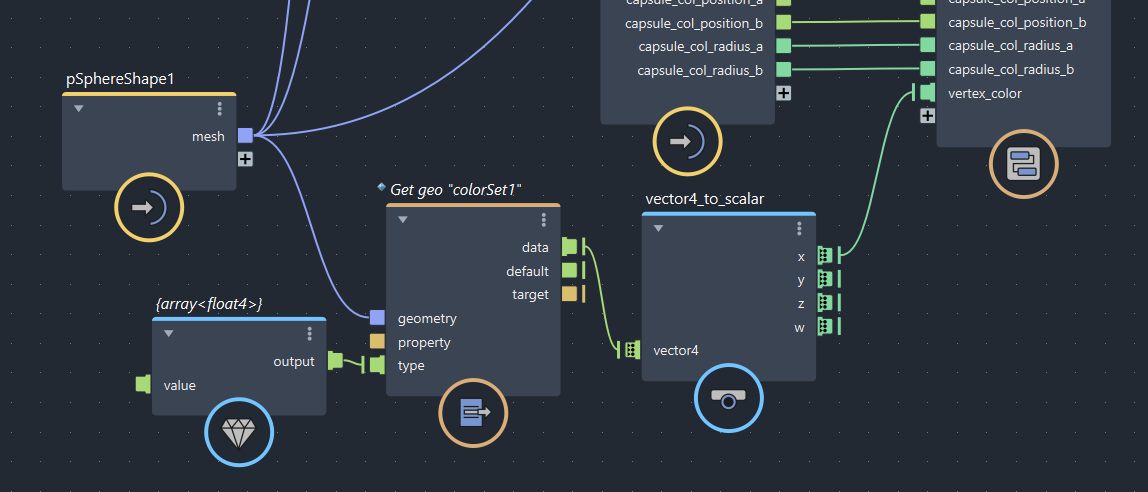
▲bifrostGraphShape
頂点カラーで初期位置とlerpします。
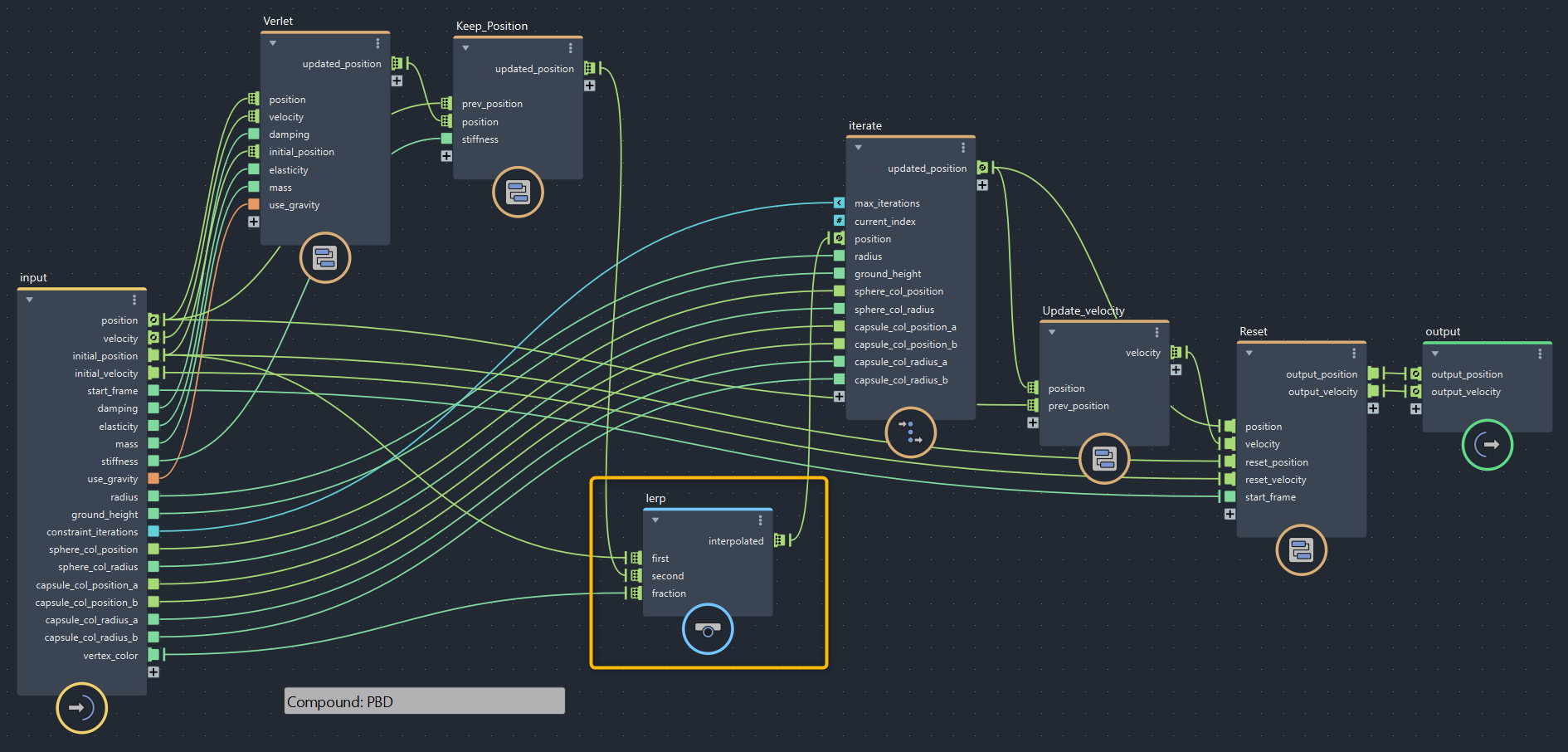
▲bifrostGraphShape > pbd
動かしてみると、やわらかプリンができました🍮
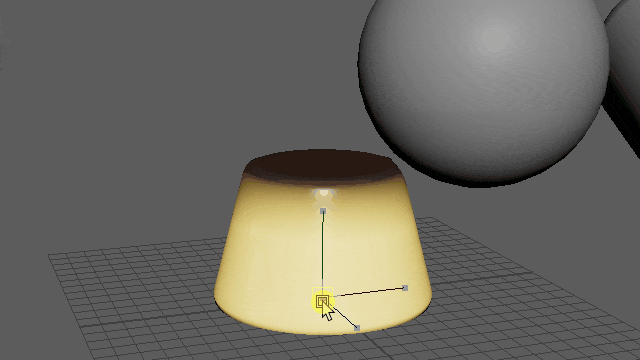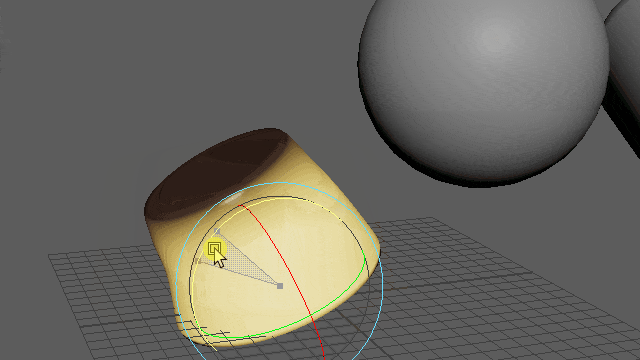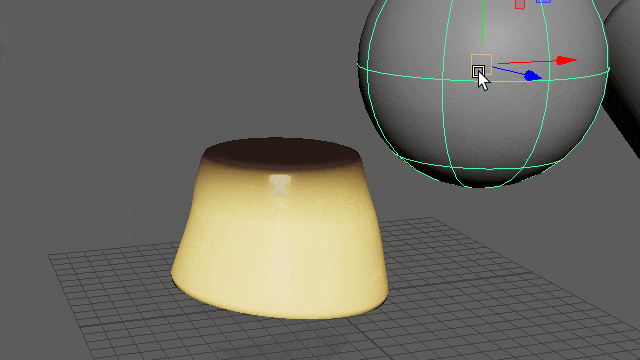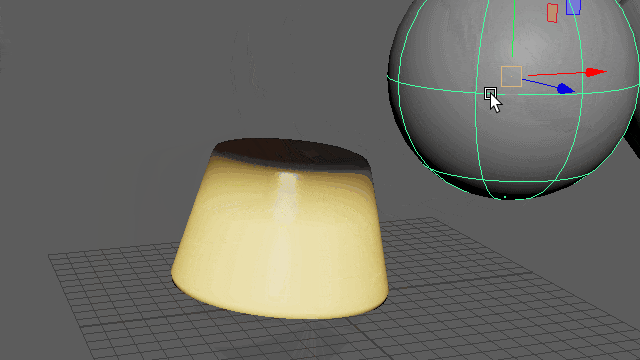
▲※重力はオフにしてます
両端が固定のカーブ
わりと大変なやついきます。
第3回の「片方が固定の距離制約」と「両方がフリーの距離制約」の合わせ技です。第4回の「コリジョンによる補正」も入ってます。
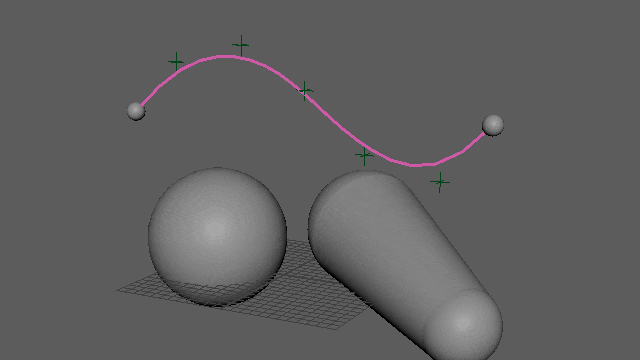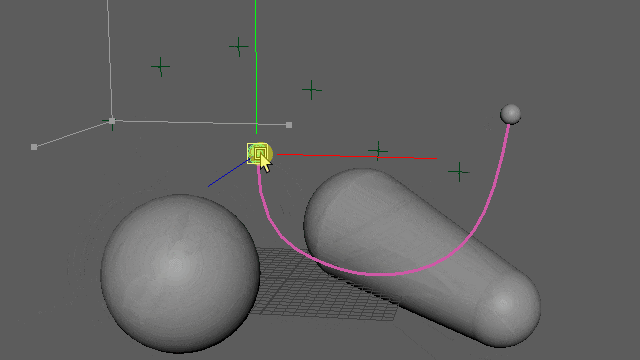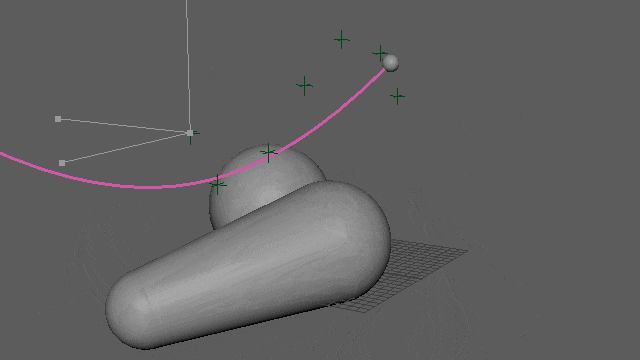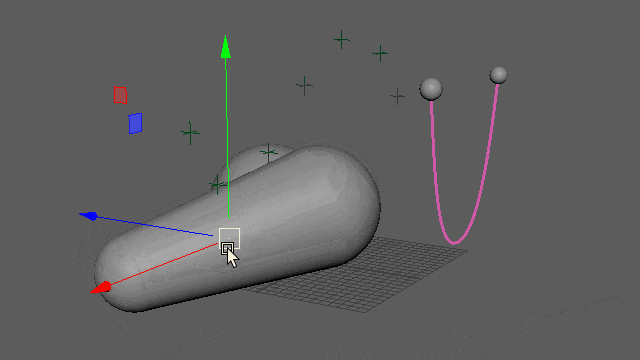
全7点中、両端の2点が固定、中間の5点はpbdで制御です。距離制約は計6つ、うち4つ（二重線）は「両方がフリーの距離制約」になります。
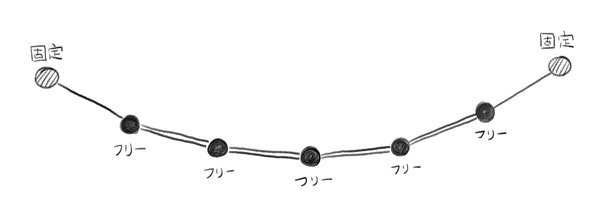
もはやグラフはお見せしたところで感があります…
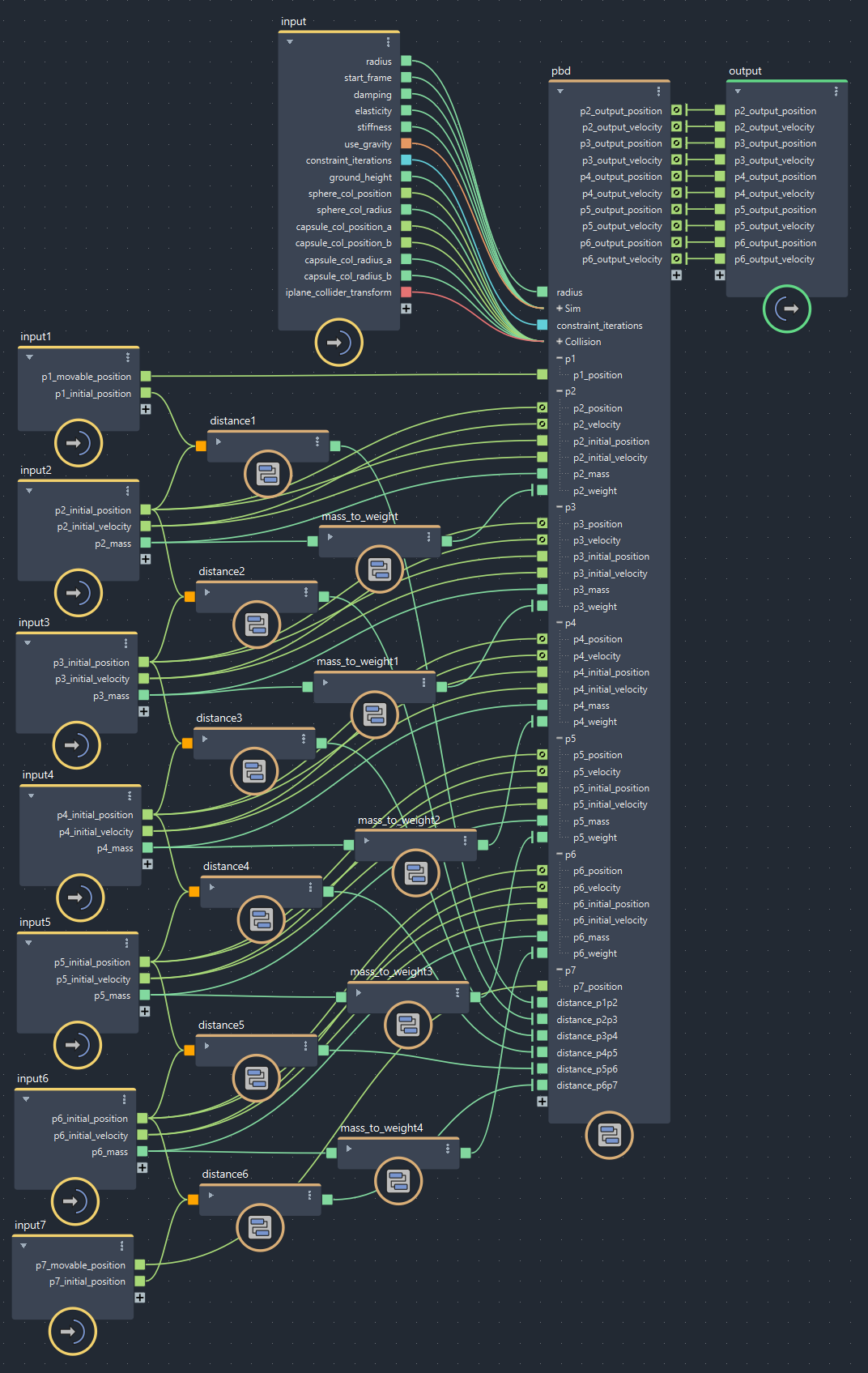
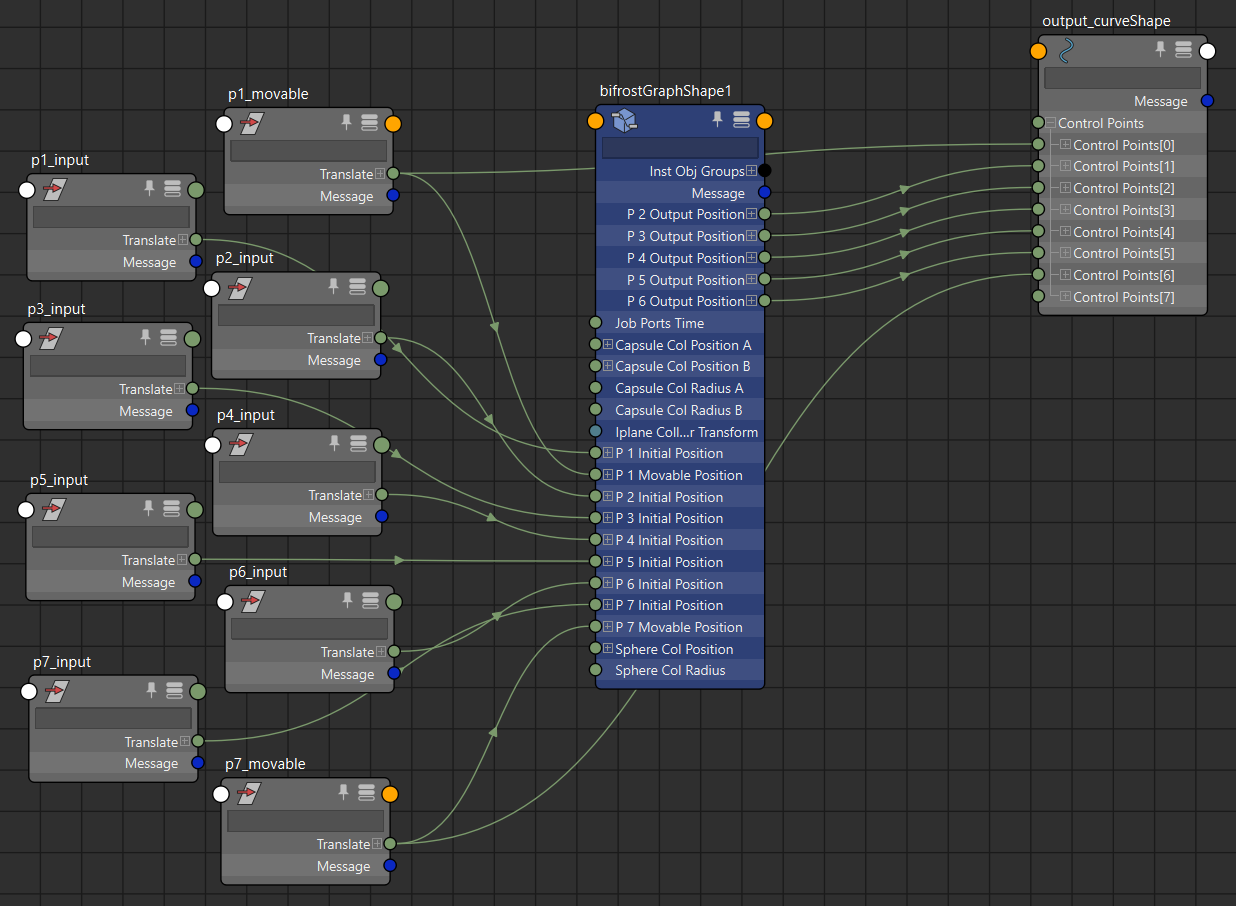
▲bifrostGraphShape
ものすごく複雑に見えるんですが、制御点の数が多いだけでベースは第3回の「両方がフリーの距離制約」の型 になってます。位置補正が複数あるので中央付近でiterateにまとめてあります。
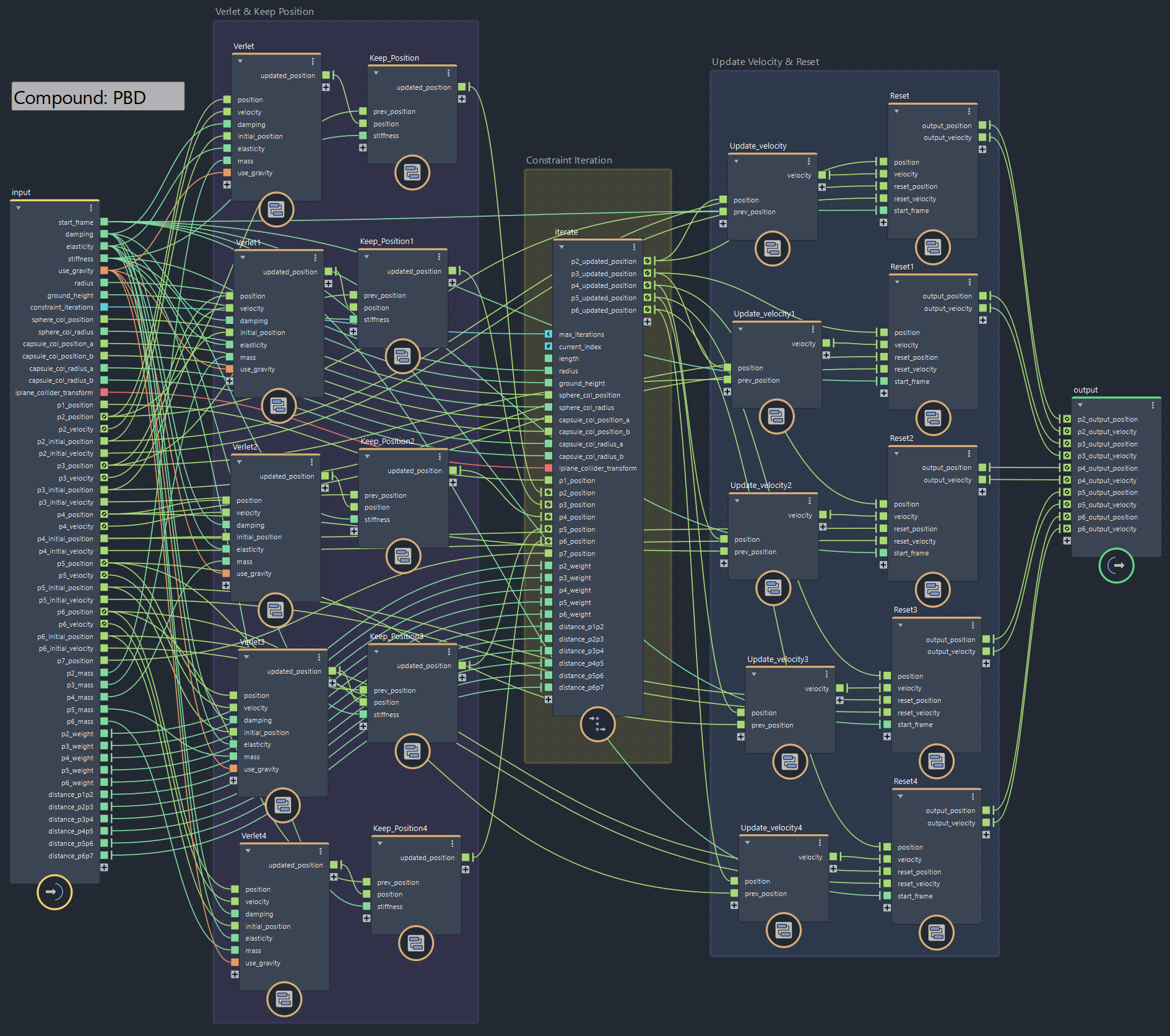
▲bifrostGraphShape > pbd
重要なのはイテレーション内です。中間の5点については複数の距離制約から引っ張られるので、これも反復法で収束させる必要があります。具体的には以下のリンクのヤコビソルバと呼ばれる方法で組みます。『制約をそれぞれ別に計算してから平均を取る』 を反復でぶん回します。
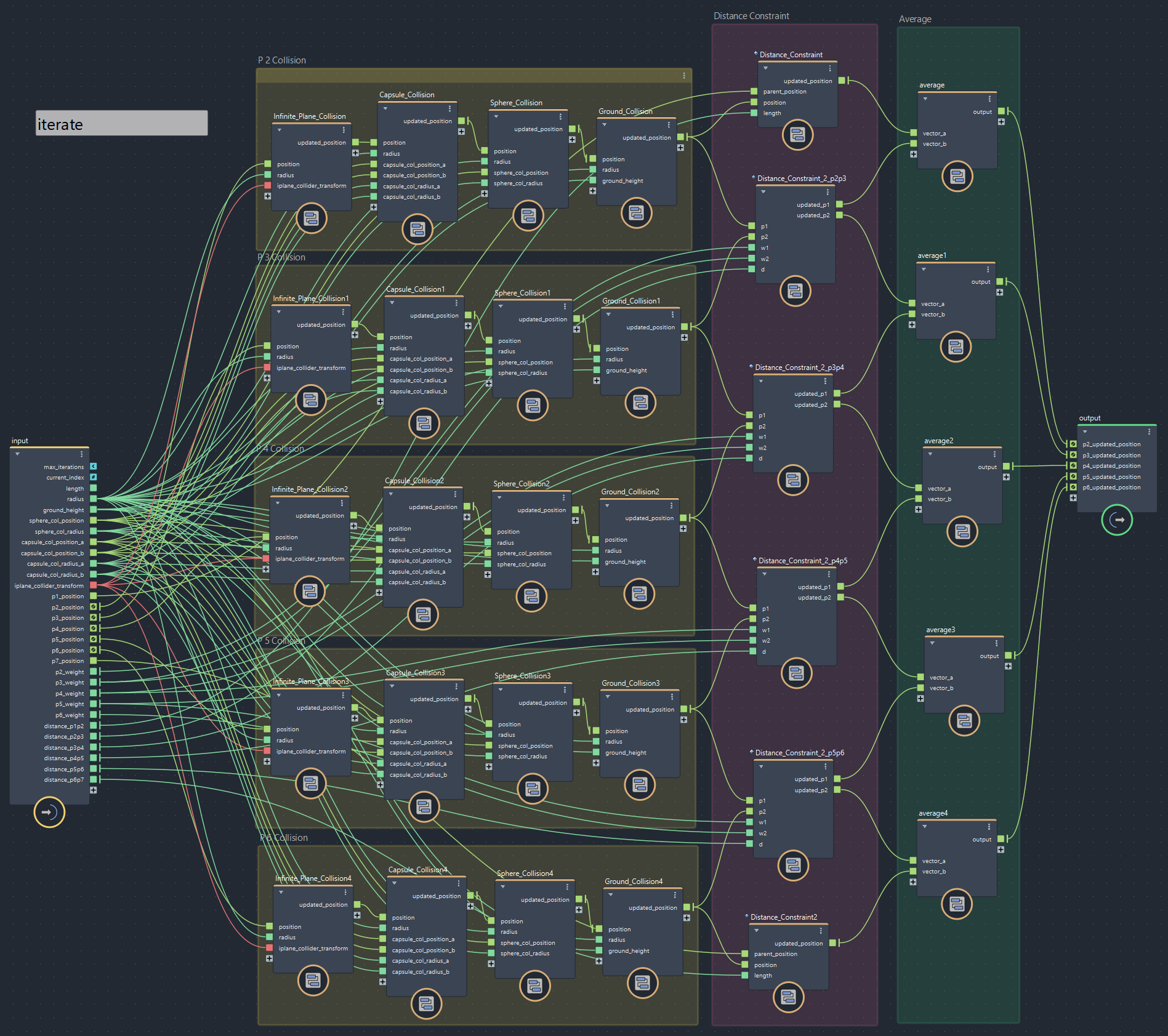
▲bifrostGraphShape > pbd > iterate（右端のaverageが平均をとっているところ）
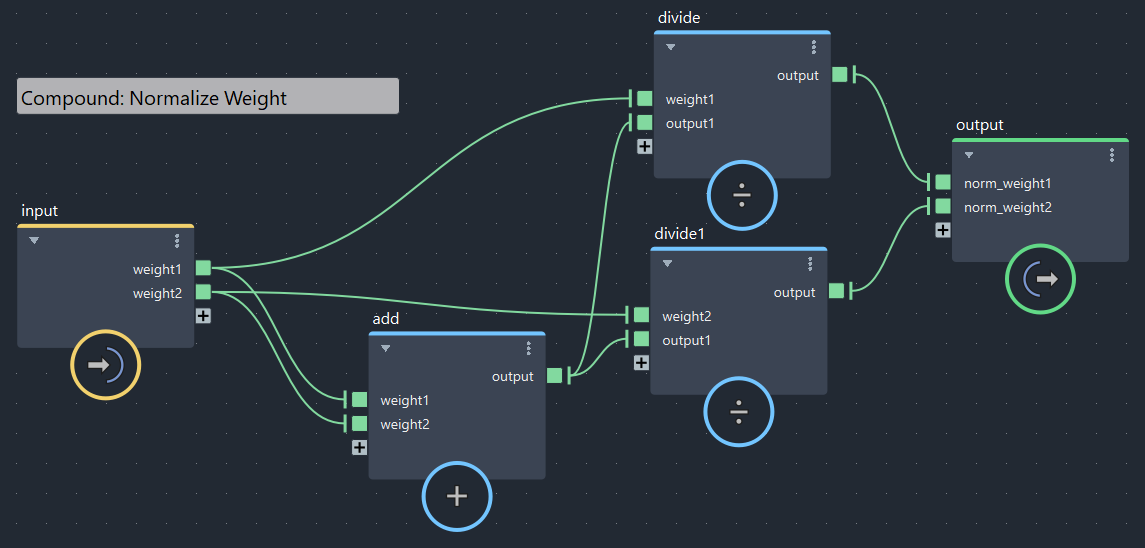
平均は足して2で割るだけです。
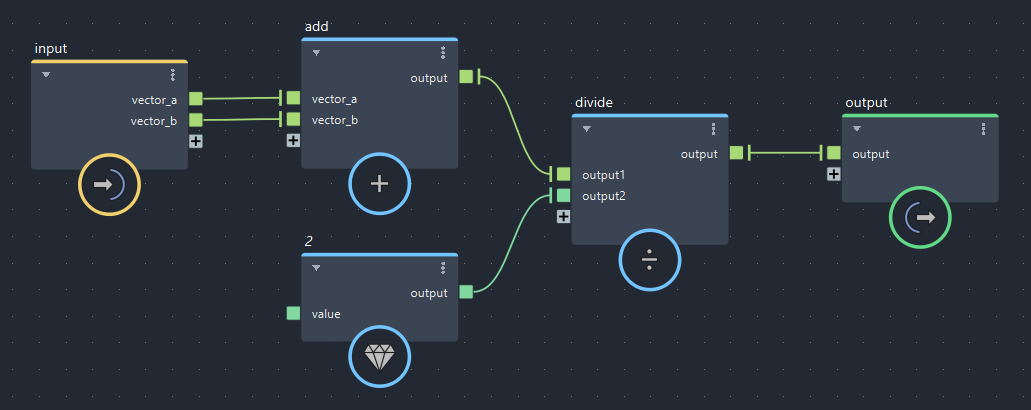
▲bifrostGraphShape > pbd > iterate > average
Mayaからの入力はシンプルです。
ちなみに、シミュレーション関連を省いて距離制約のイテレーションだけにするとこのようになります。収束していく様が見て取れます。👇
どこも固定されていないカーブ
さっきのパターンから両端を取り除いちゃいます。全5点、全てフリーです。
前項のものとだいたい同じなので諸々省きますが、両端の「片方固定の距離制約」関連を消しただけです。
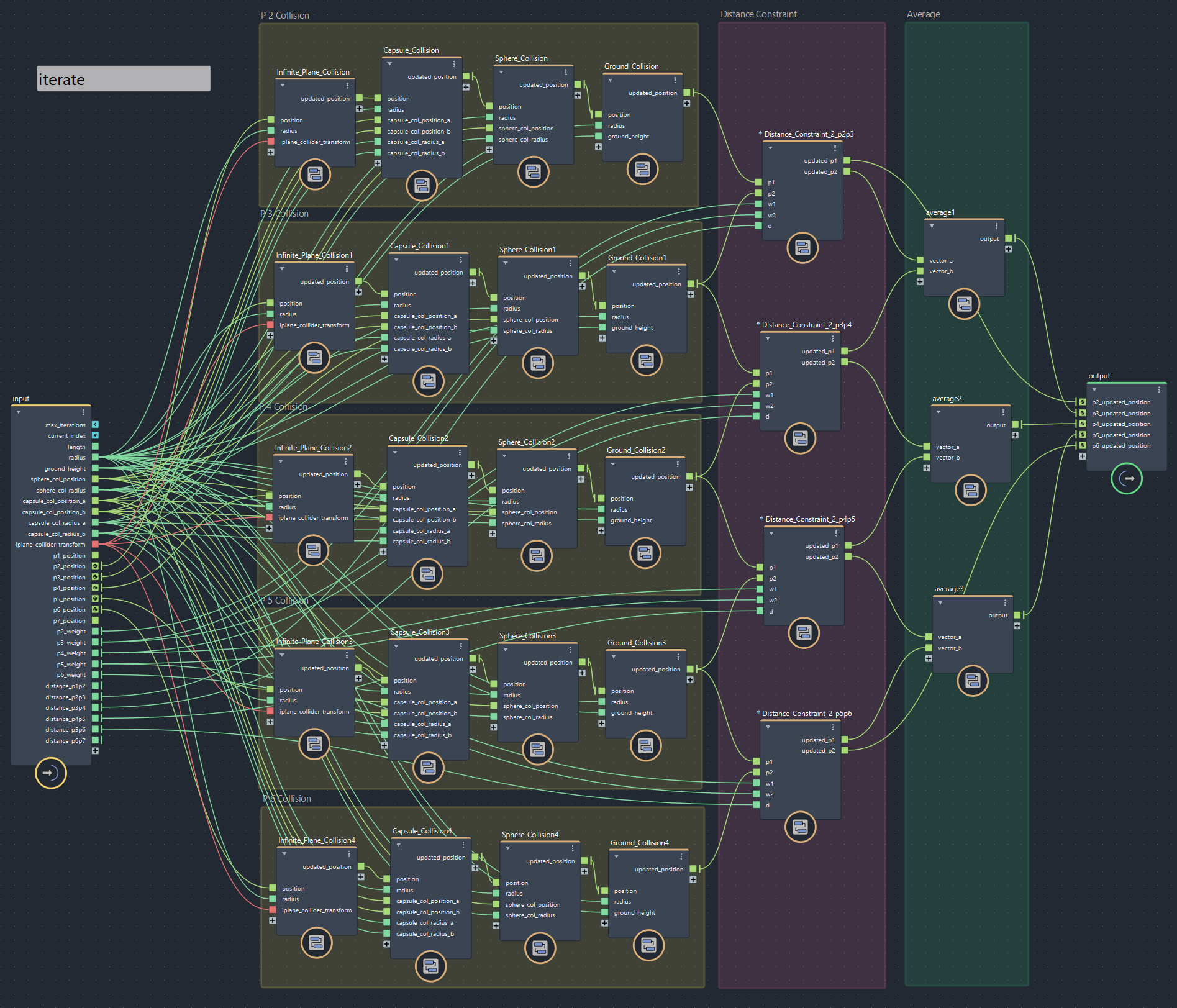
▲bifrostGraphShape > pbd > iterate
Mayaからの入出力はこんな感じ
ちょっと今回は複雑そうな見た目のものが多かったですが、前回までの基本形を「たくさん繰り返しただけ」です。入出力のほとんどが位置（3次元ベクトル）でしたし、落ち着いて分解すればひとつひとつはだいぶシンプルかと思います。
さらにここから1軸回転に限定したパターンとか角度制限とか追加していくとラグドールも作れちゃいそうです。あとは、メッシュの全エッジに距離制約を適用すれば布もできるはずです。今の組み方では量的に不可能に近いですが…
次回は、、、
ありません！ここまでお付き合い頂きありがとうございました！！！
おしまい。🙇
今までのグラフまとめ
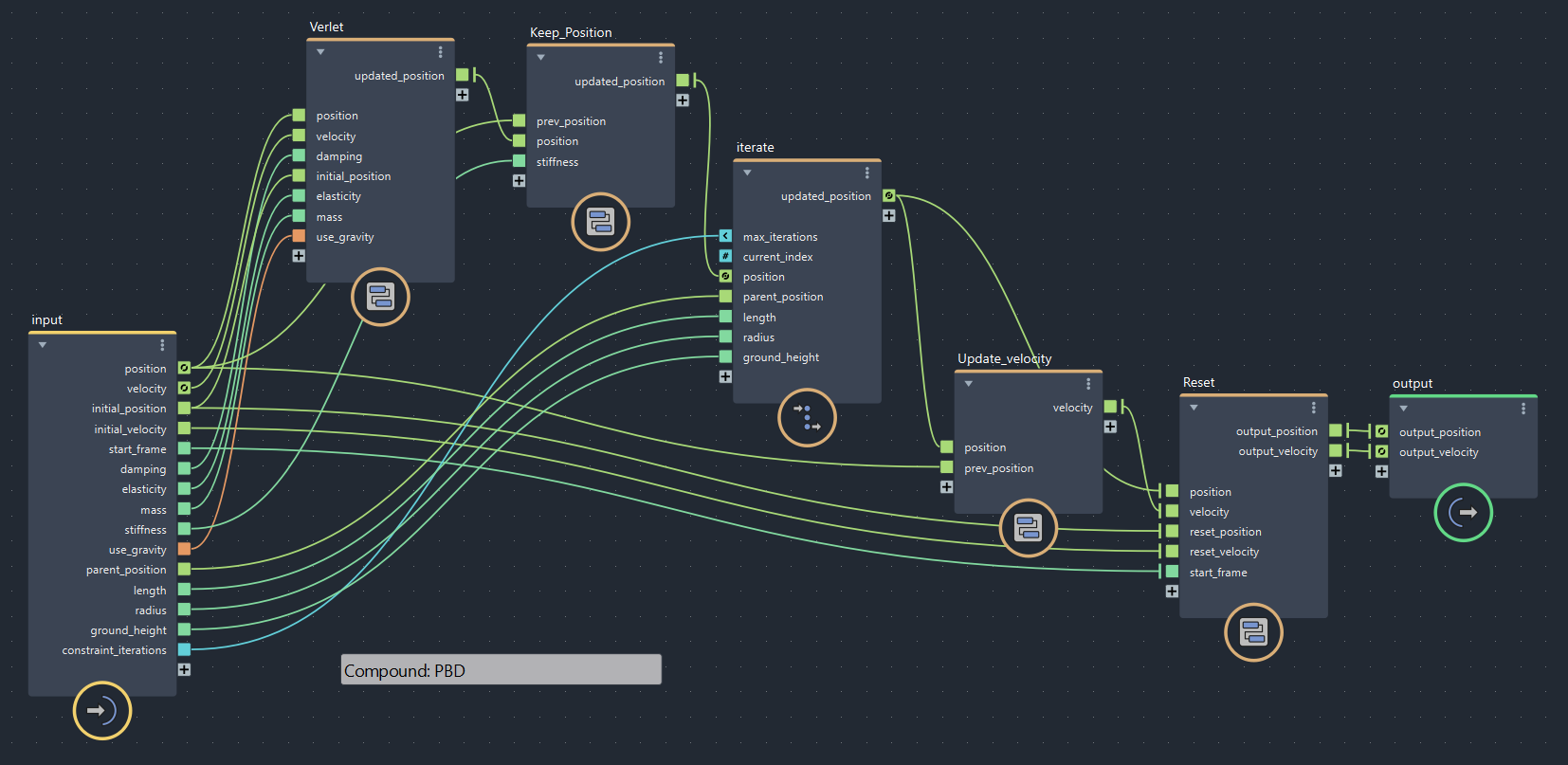
【第4回より】PBD（bifrostGraphShape > pbd）
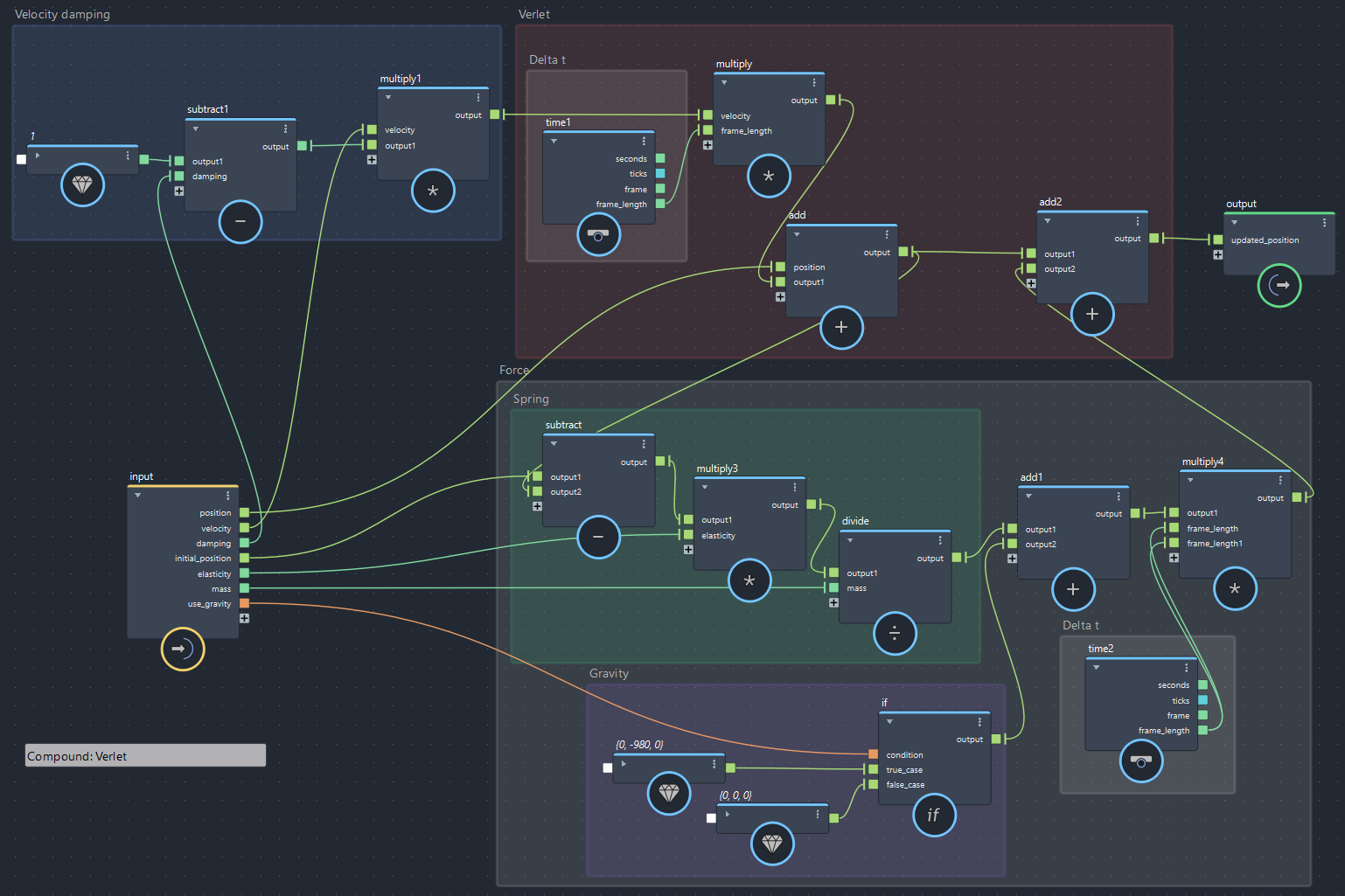
【第2回より】重力とバネを加味して次の位置を決定（bifrostGraphShape > pbd > Verlet）
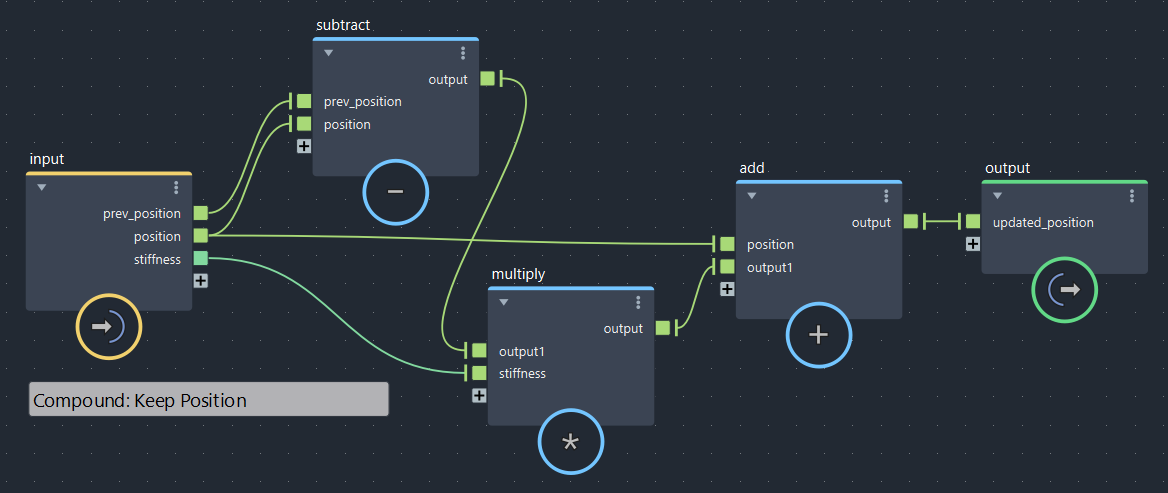
【第2回より】補正前の位置に戻す（bifrostGraphShape > pbd > Keep_position）
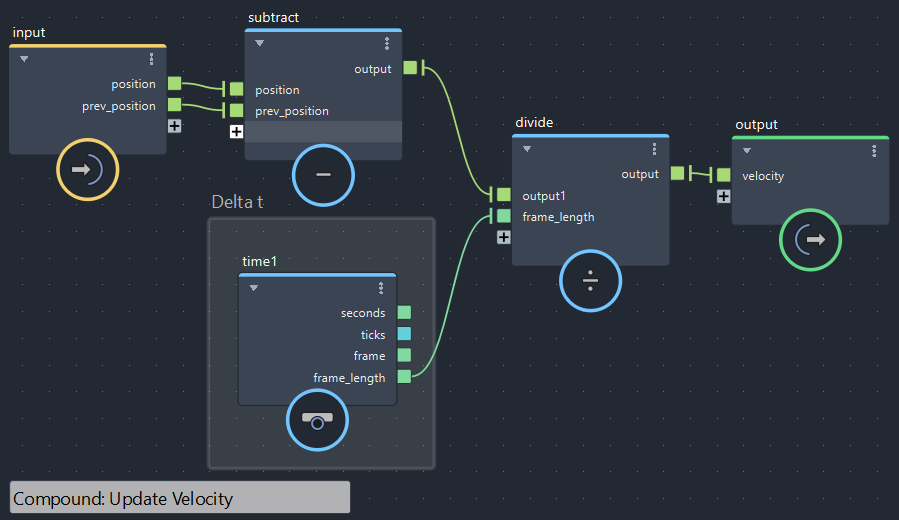
【第1回より】速度の更新（bifrostGraphShape > pbd > Update_Velocity）
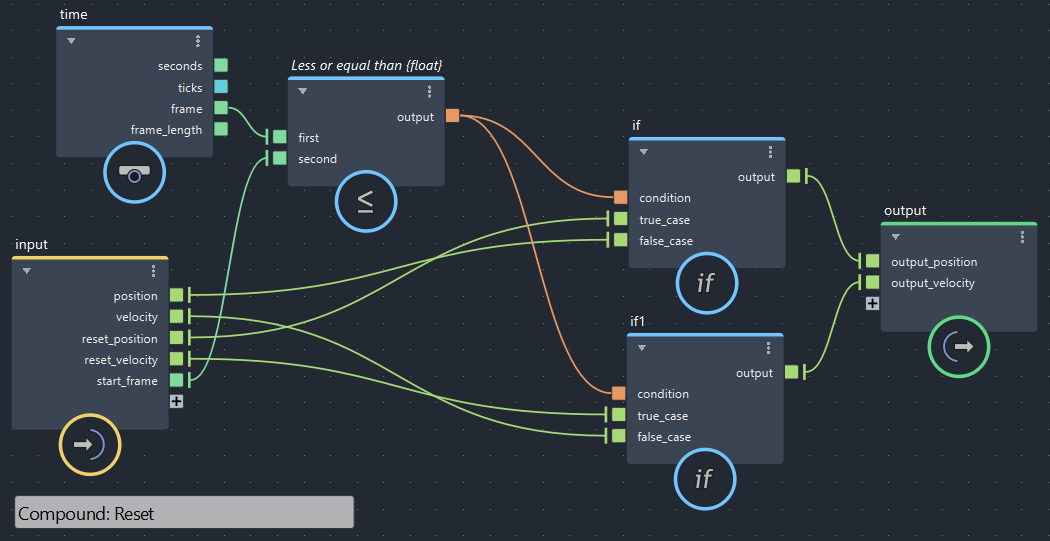
【第1回より】初期値へリセット（bifrostGraphShape > pbd > Reset）
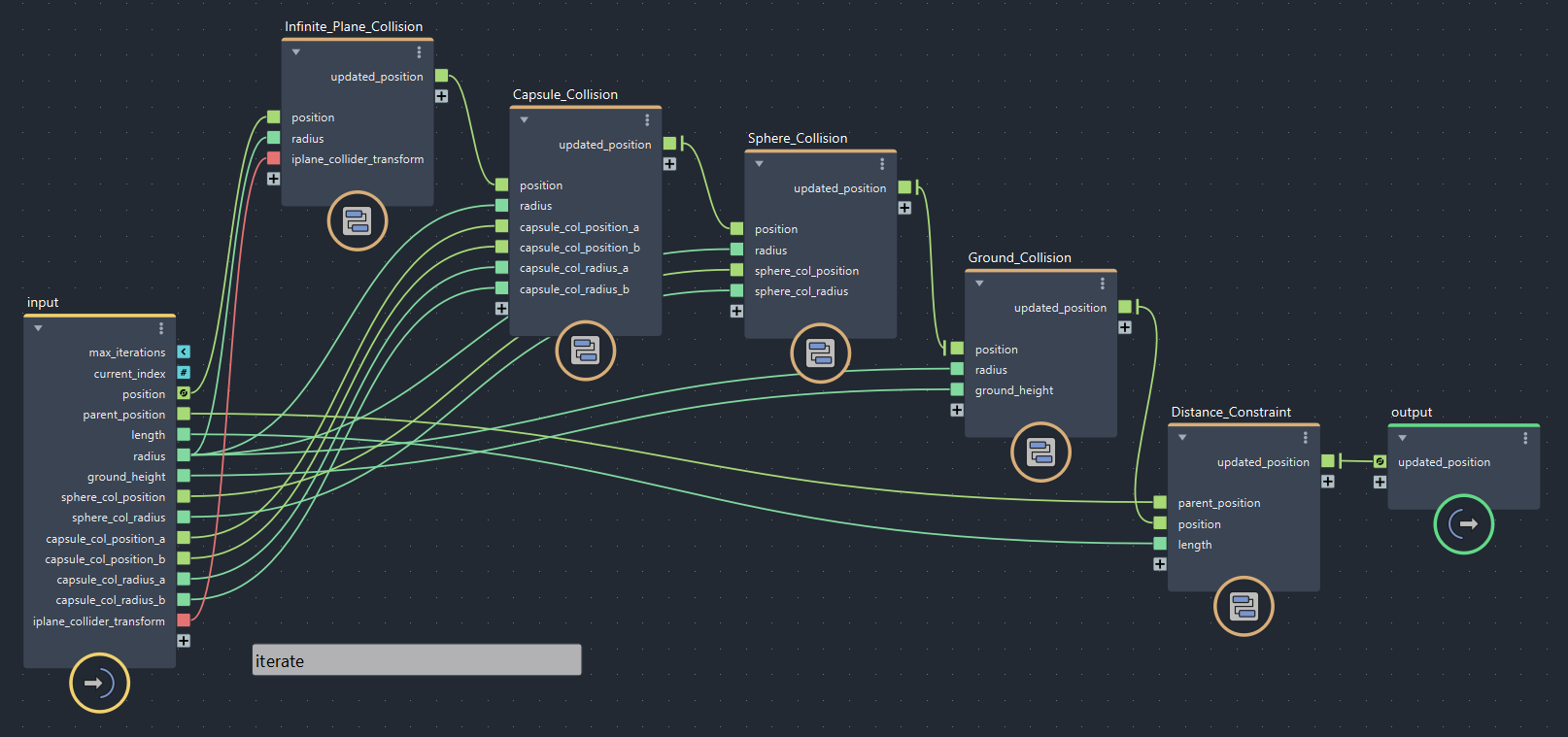
【第4回より】制約のイテレーション例（bifrostGraphShape > pbd > iterate）
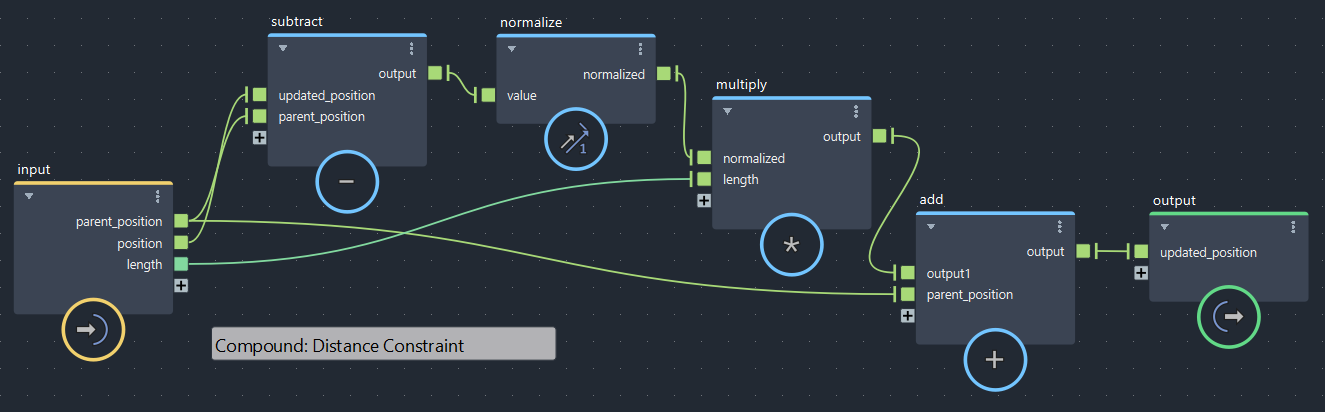
【第3回より】距離制約①：片方が固定（bifrostGraphShape > pbd > iterate 内で使用）
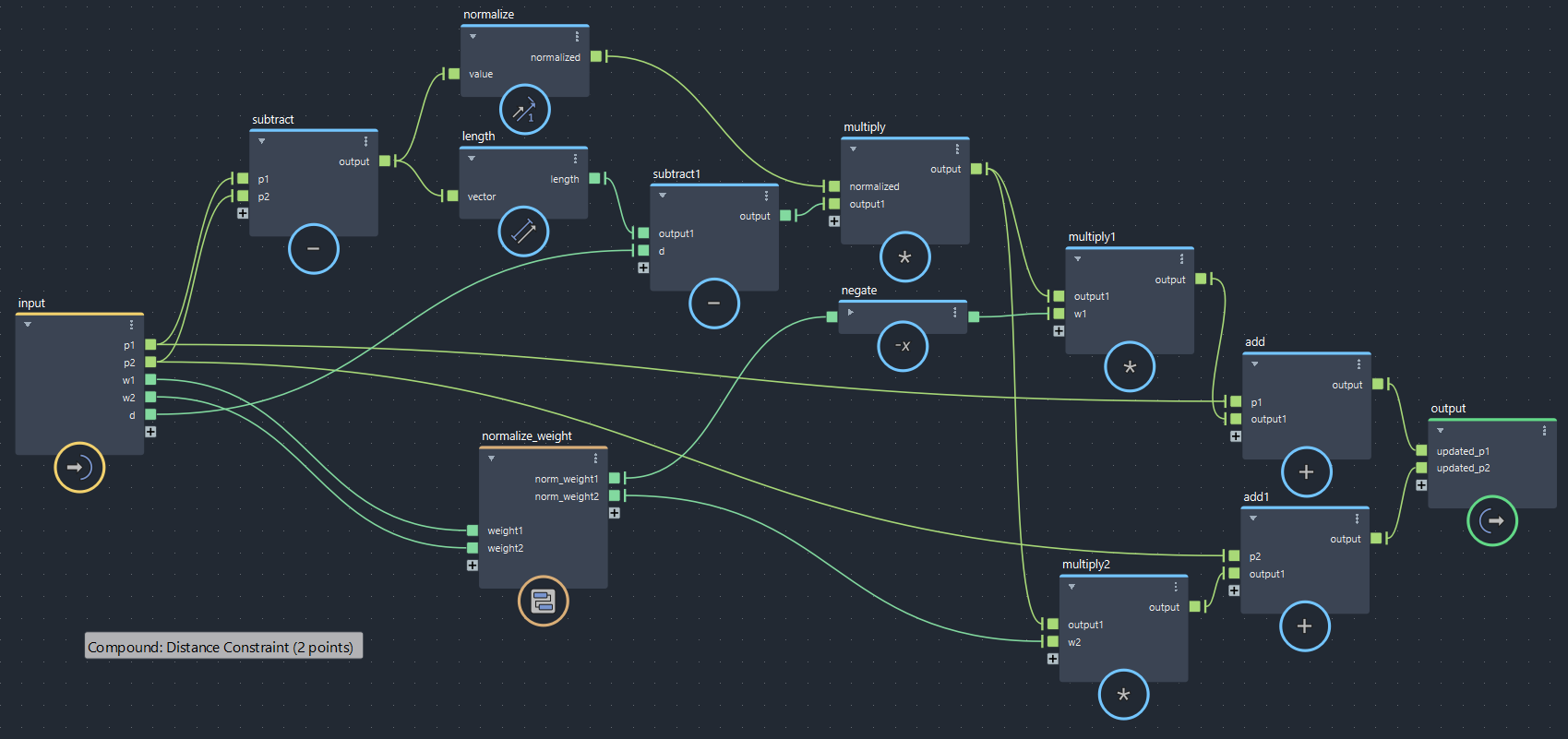
【第3回より】距離制約②：両方がフリー（bifrostGraphShape > pbd > iterate 内で使用）
【第3回より】質量からウェイトを計算
【第3回より】ウェイトの正規化
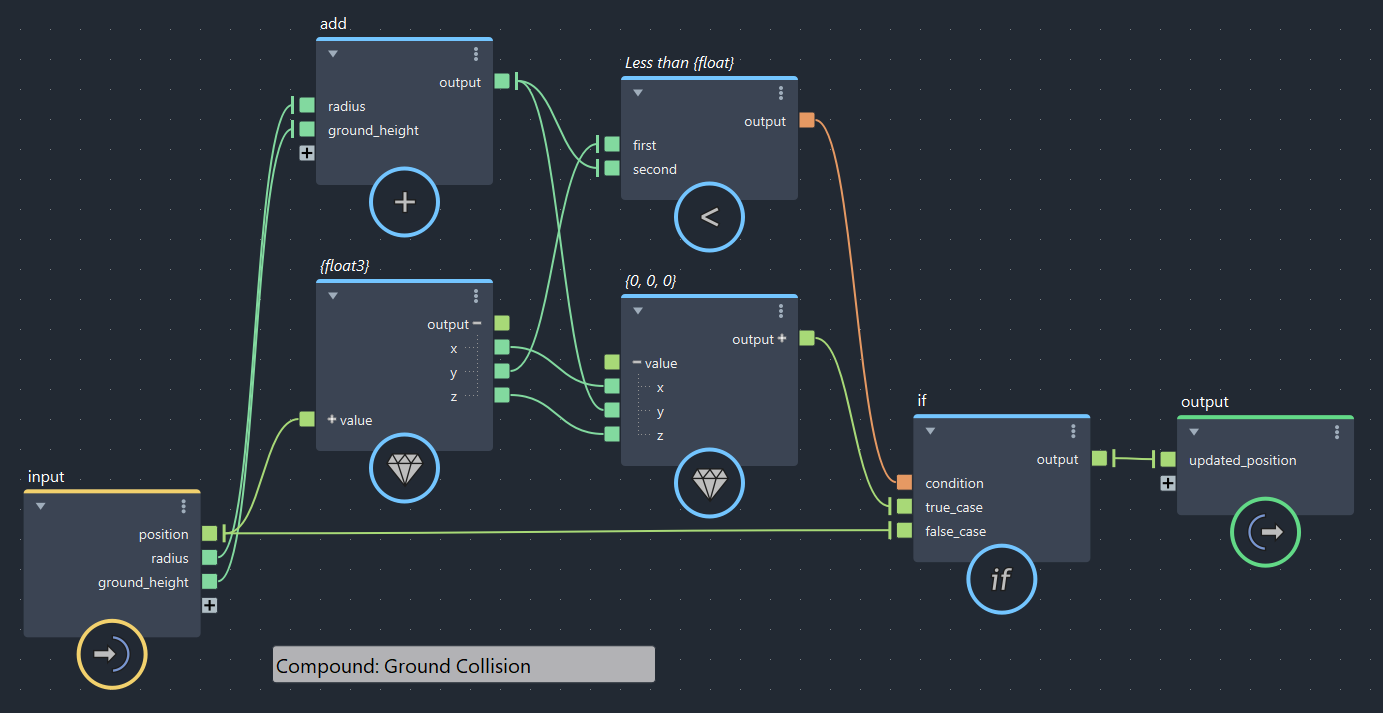
【第4回より】地面コリジョン（bifrostGraphShape > pbd > iterate 内で使用）
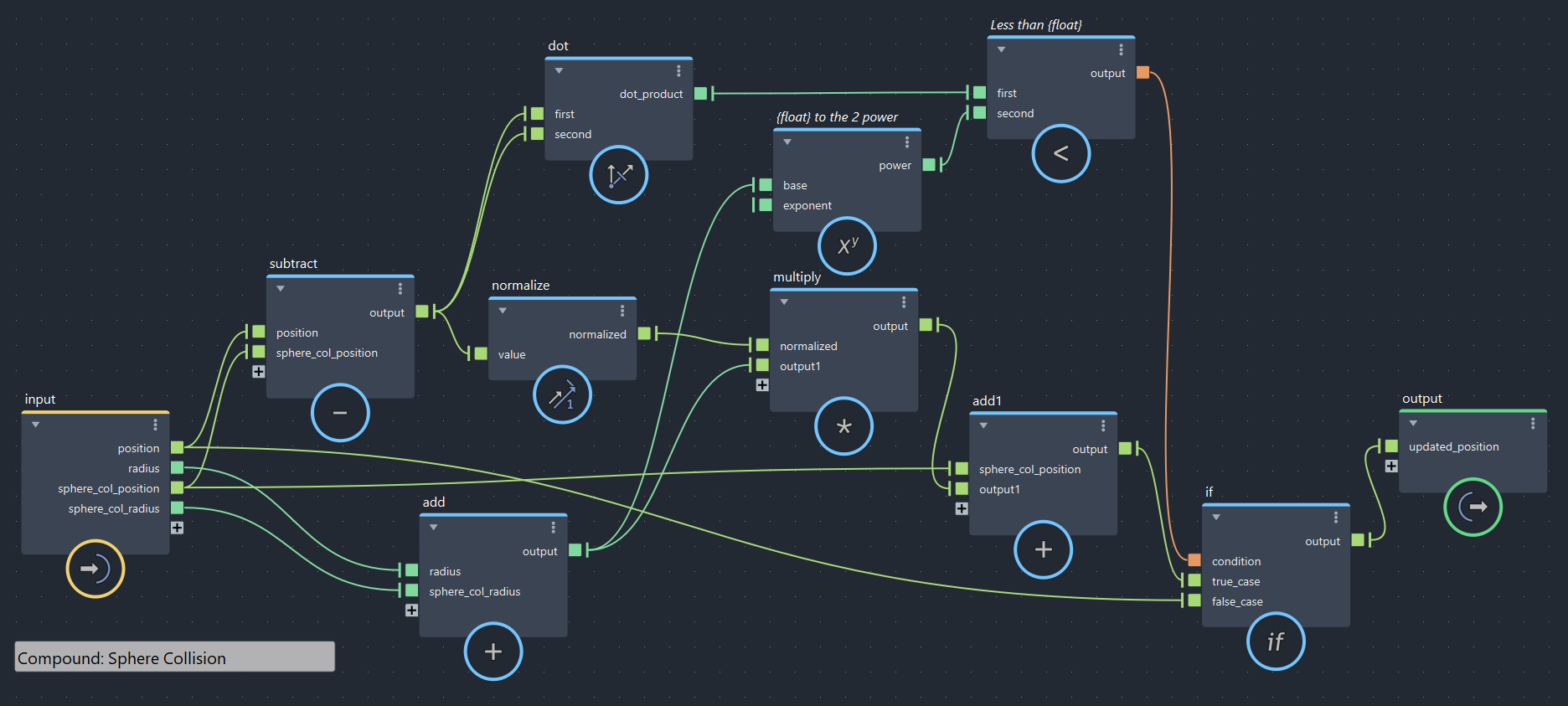
【第4回より】球コリジョン（bifrostGraphShape > pbd > iterate 内で使用）
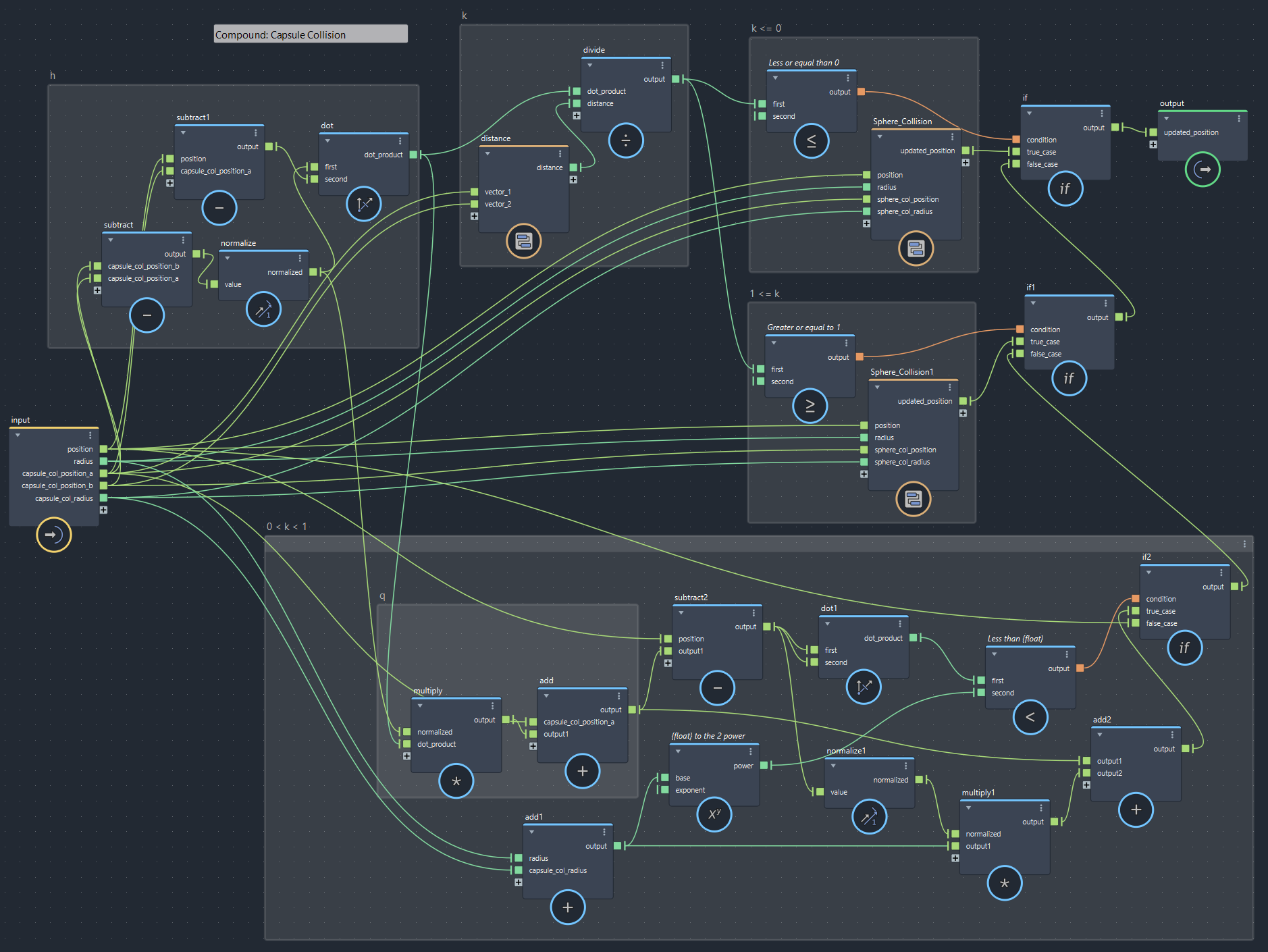
【第4回より】カプセルコリジョン：半径共有（bifrostGraphShape > pbd > iterate 内で使用）
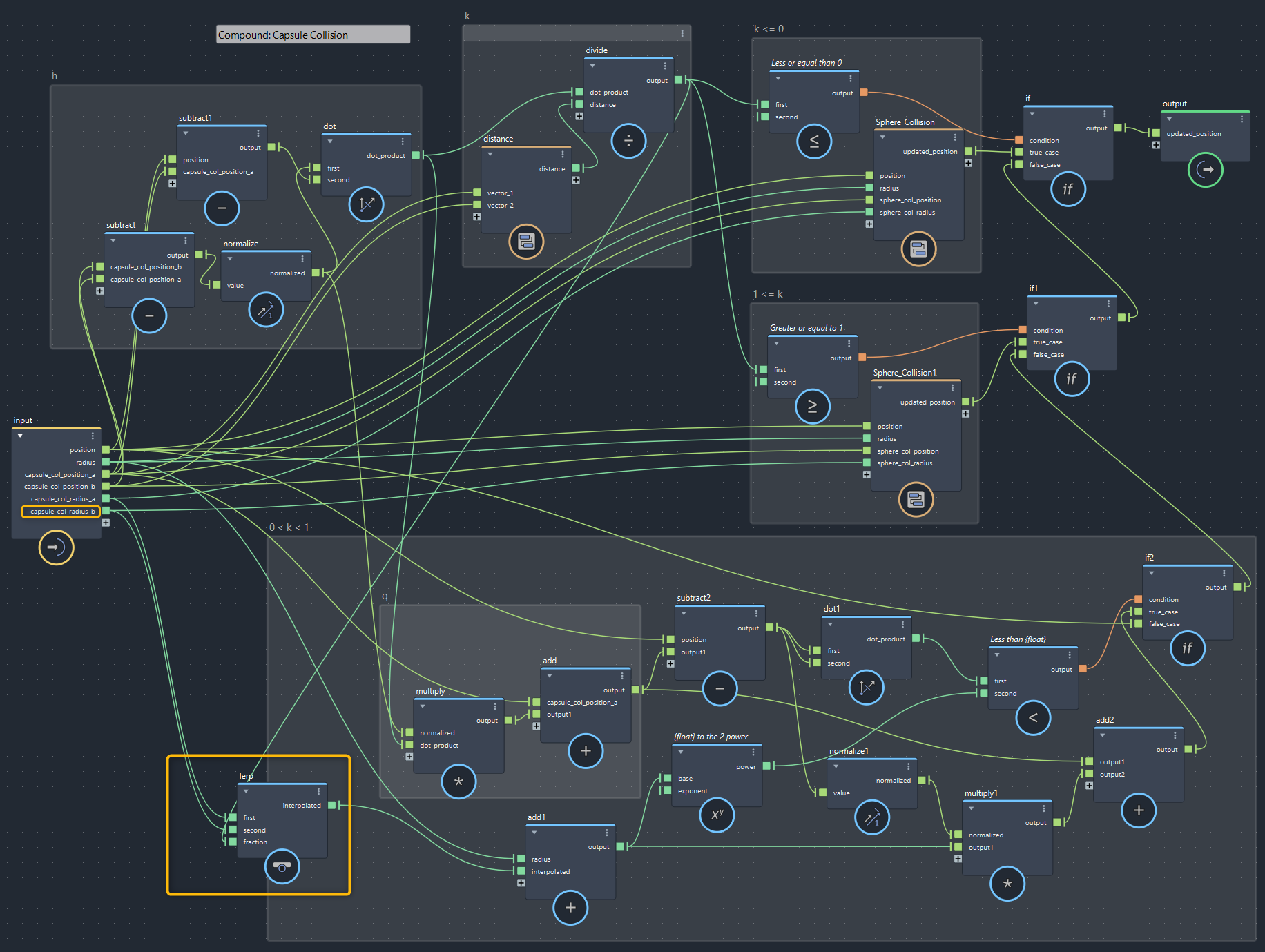
【第4回より】カプセルコリジョン：半径個別（bifrostGraphShape > pbd > iterate 内で使用）
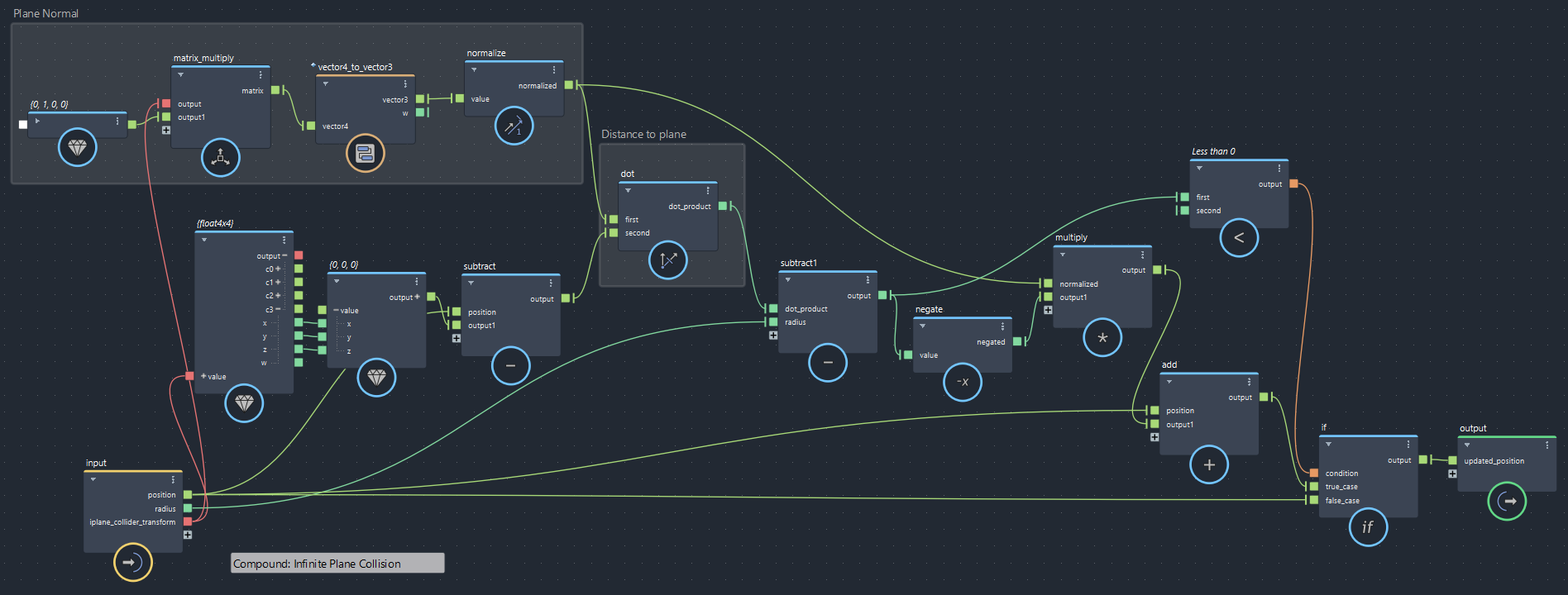
【第4回より】無限平面コリジョン（bifrostGraphShape > pbd > iterate 内で使用）
成果物（コンパウンド／グラフサンプル）
ここまでに作成したコンパウンドとグラフはこちらのリポジトリに置いてあります。
前の記事