ハイどうもこんにちは!
前回と同じ要領で、導き出された位置を直接操作しコリジョンによる押し出しを加えていきます。ここで取り上げるコリジョン形状は球やカプセルなどのシンプルなプリミティブです。
さっそく始めていきます。
地面(水平固定の無限平面)
最も簡単な例です。何も難しい計算はありません。点$p$の位置座標$(p_x,p_y,p_z)$のうち$p_y$が地面の高さ+半径より下に埋まっていたら高さ+半径で上書きするだけです。
こうなっていたら、
p_y < h + r_p
こうします。
p_y = h + r_p
$h$は地面の高さ、$r_p$は点の半径です。
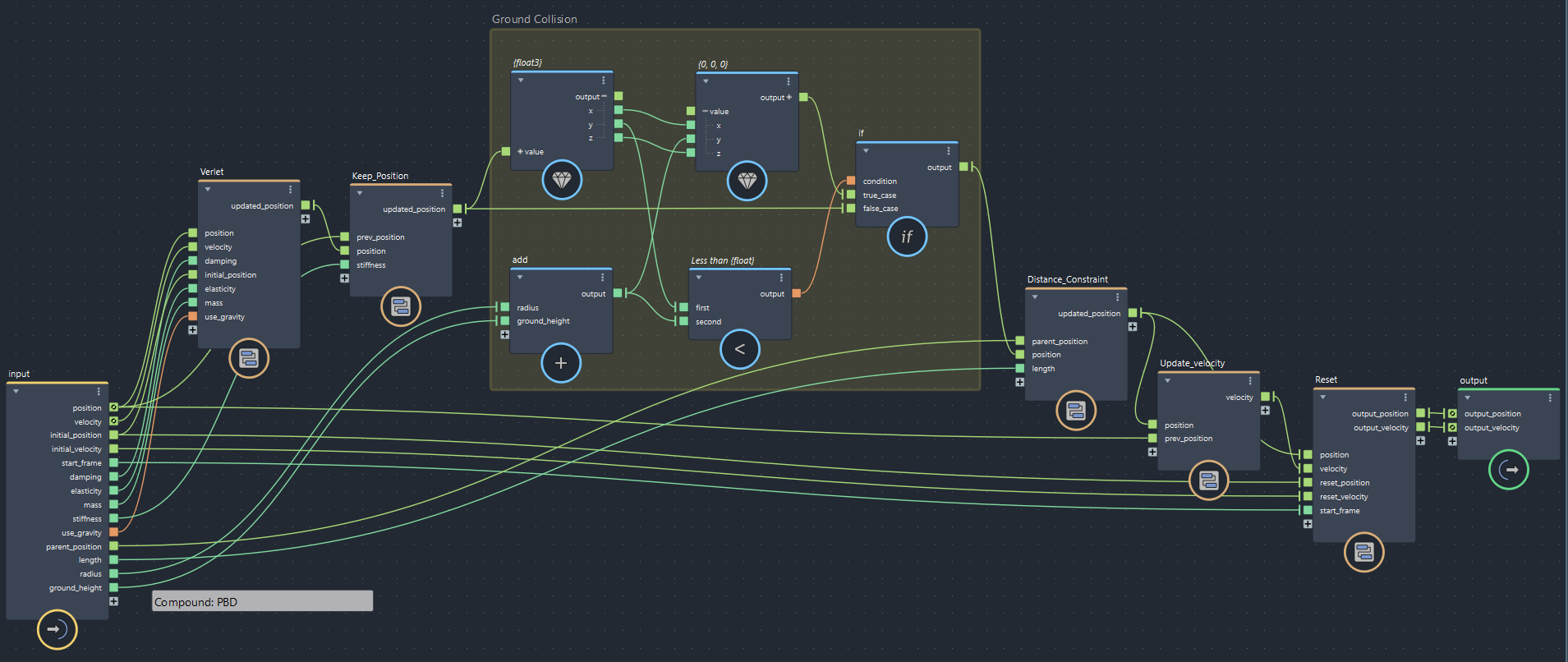
ベースのBifrostグラフは第3回の「片方が固定の距離制約」が入ったものを使い、次のように地面コリジョンを追加します。
が、ここで困ったことがあります。前回「制約は絶対!」と言って速度更新の直前に距離制約を足したのですが「コリジョンも絶対!」でないと困ります。2つの条件を同時に満たす良い感じの場所を見つけたいです。

▲後の距離補正により地面コリジョンの補正結果が壊されている
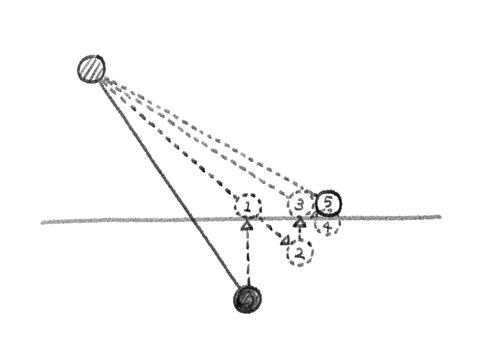
そこで、同時に満たしたい複数の位置補正をiterateの中に放り込みます。『コリジョン補正(①)の後に距離補正(②)をしたらコリジョンにまた埋まったので、もう一度コリジョン補正(③)して、そしたら今度は距離がずれたのでまた補正(④)して、、、』 という具合に何回か繰り返すといい感じの場所に収束します。いわゆる反復法というやつです。
グラフはこのようになりました。
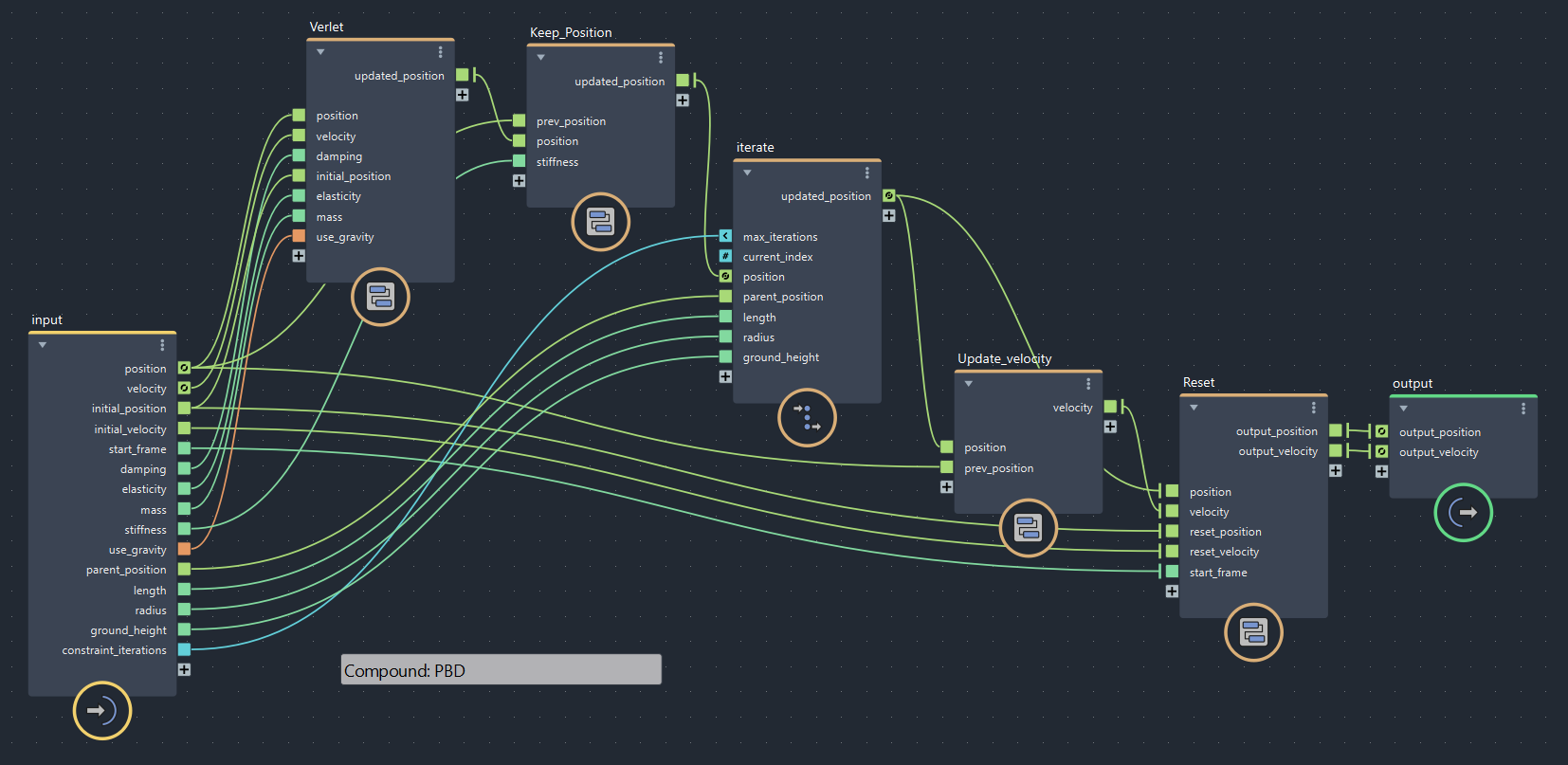
▲bifrostGraphShape > pbd
positionポート、updated_positionポートをState Portに設定します。
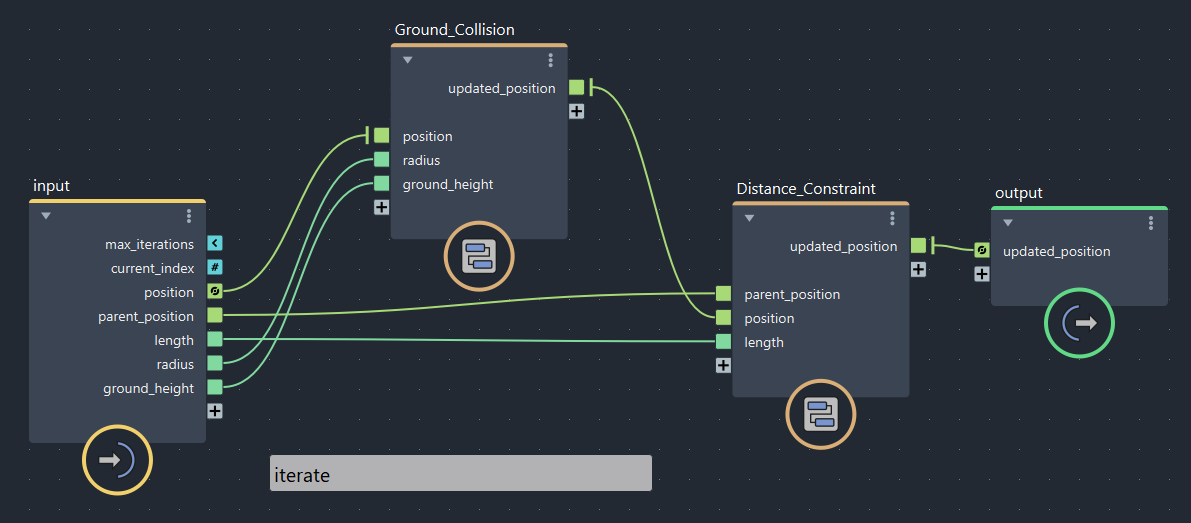
▲bifrostGraphShape > pbd > iterate
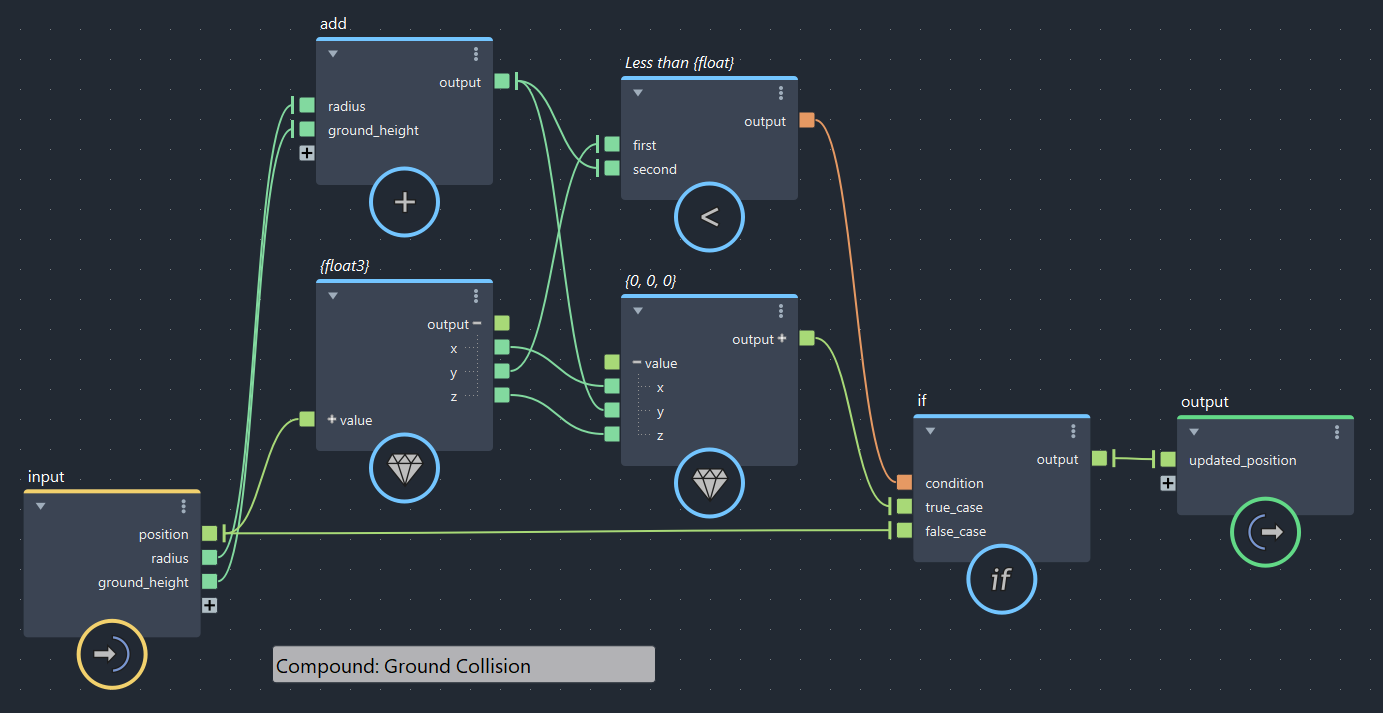
▲bifrostGraphShape > pbd > iterate > Ground_Collision
max_iterationsを5に設定して動かしてみると、距離制約を満たしつつ地面にも埋まりにくくなりました!

球
位置補正のイテレーションが組めたところでその他のコリジョン形状をイテレーション内に足していきます。詳細な解説はありがた〜いリンクを貼っておきますので気になる方は見てみてください。この場では最低限の説明でさらりと行きます。
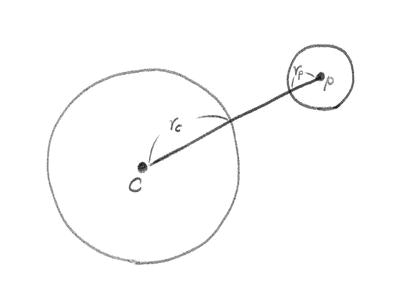
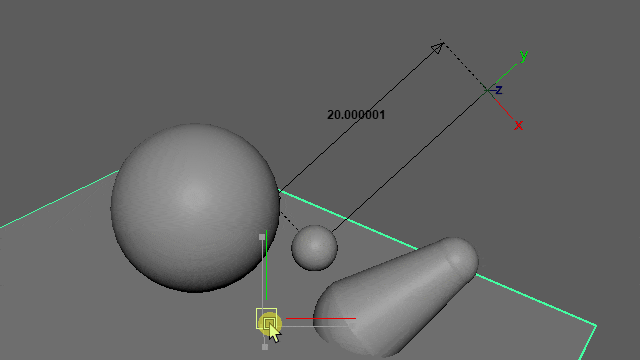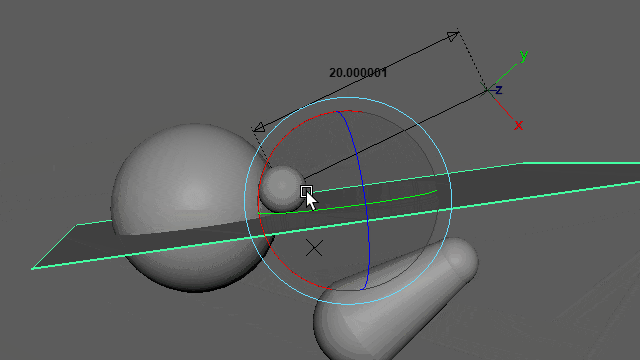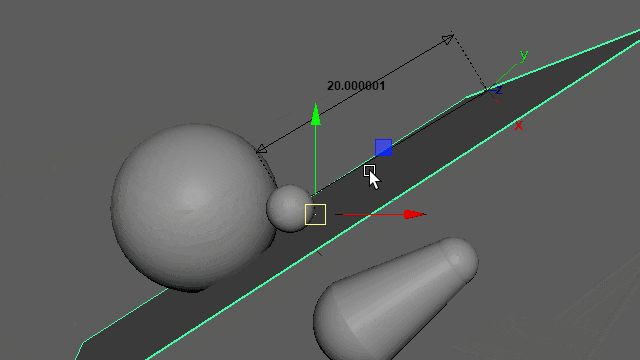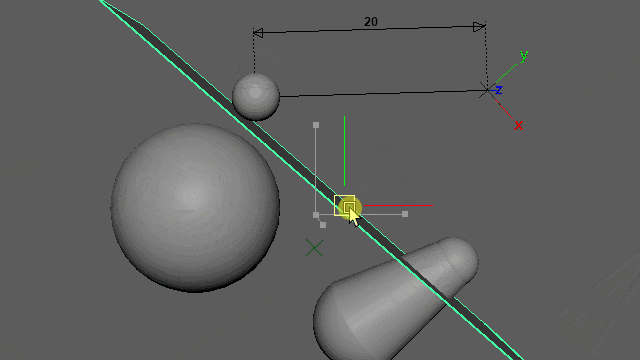
点$p$の半径を$r_p$、球コリジョンの中心を$c$、コリジョンの半径を$r_c$、とすると、$p,c$間の距離が$r_c + r_p$よりも小さかったら、衝突しています。
\| p-c \| < r_c + r_p
このとき、$cp$ベクトルの方向へ$r_c + r_p$だけ離れた位置に$p$を移動します。
p' = c + \frac{p-c}{\|p-c\|} (r_c+r_p)
ちなみに、単純な大小比較が目的であれば、正確な距離を測る必要はなく、距離の2乗を使うことで計算が重めの平方根を取り除くことができます。先ほどの衝突判定式はこちらで置き換えられます。
(p-c)\cdot(p-c) < (r_c+r_p)^2
Bifrostグラフは次のようになります。さっきの地面コリジョンも残してあります。
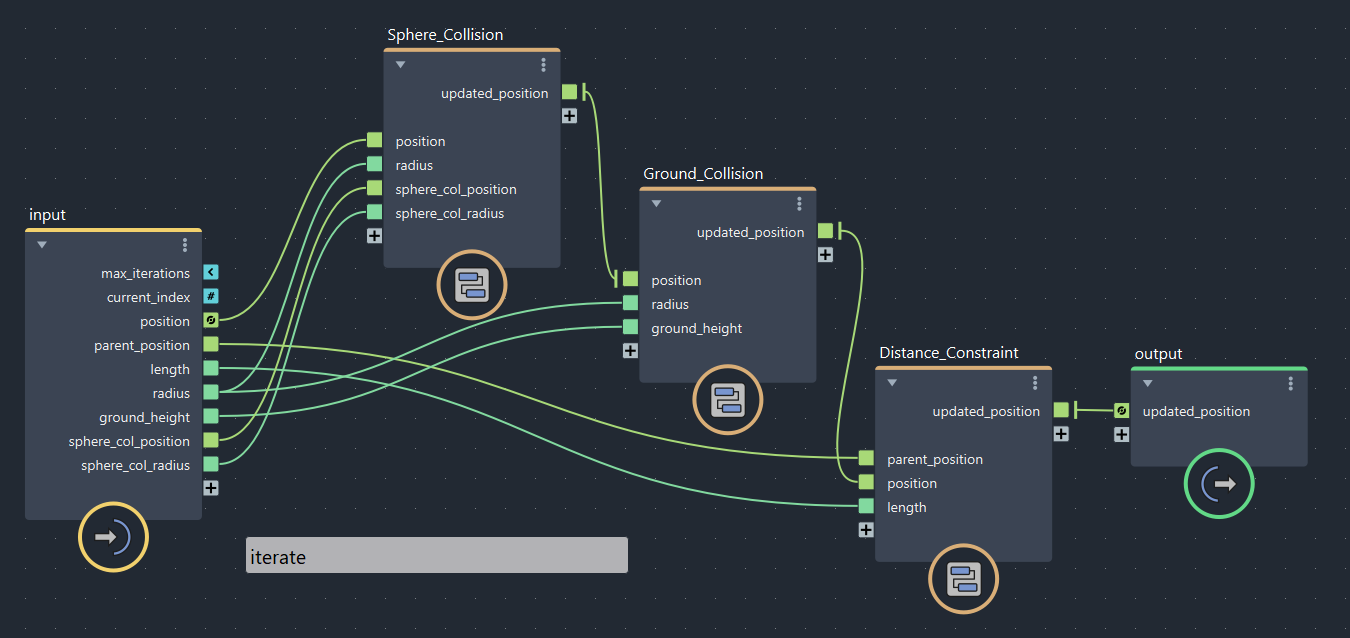
▲bifrostGraphShape > pbd > iterate
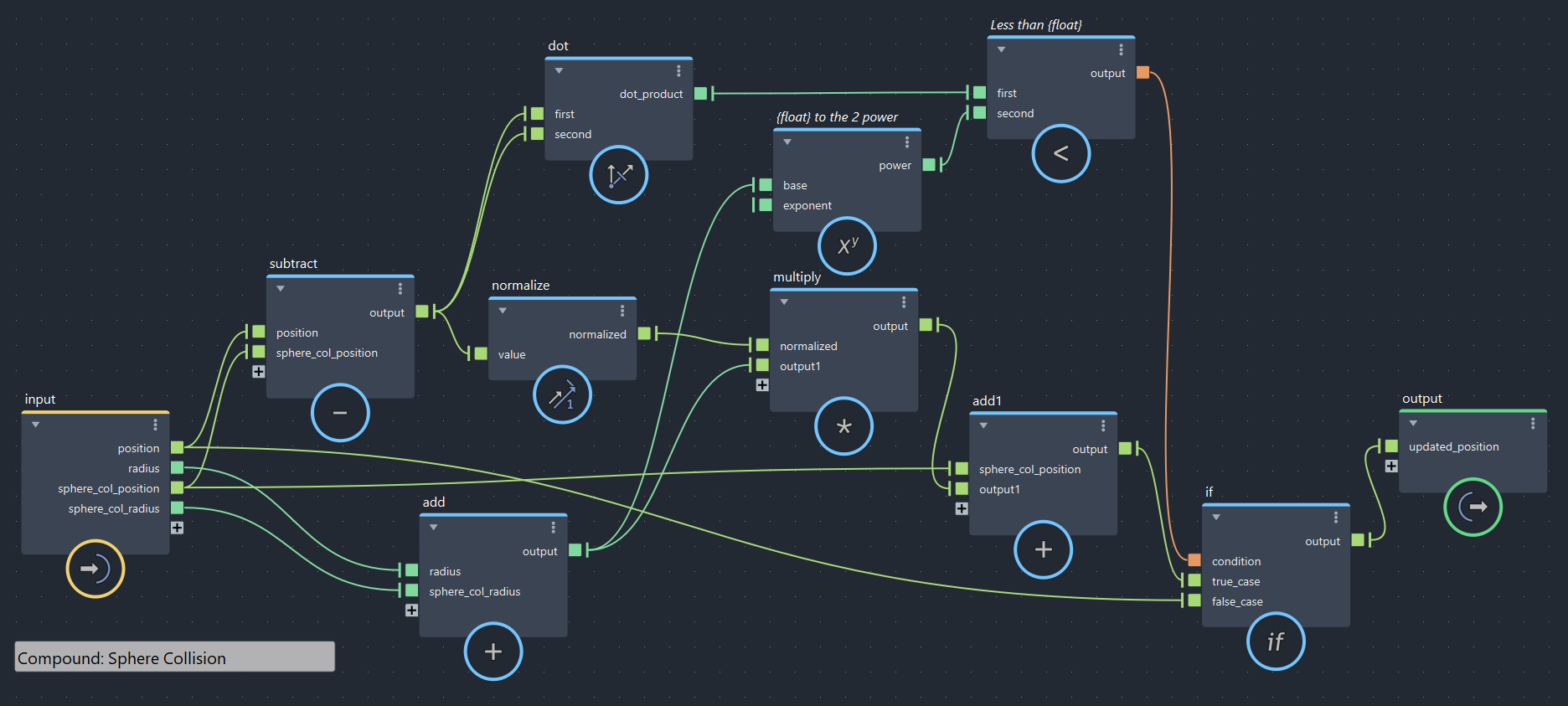
▲bifrostGraphShape > pbd > iterate > Sphere_Collision
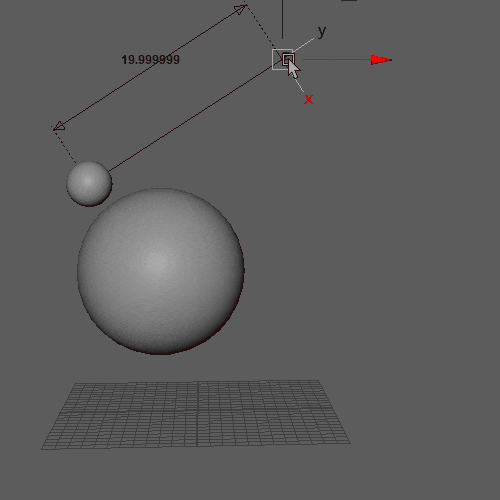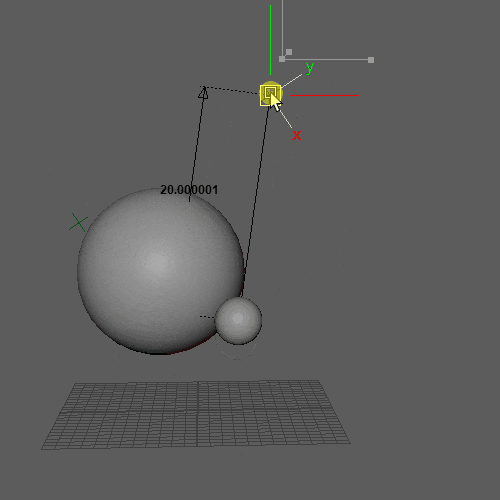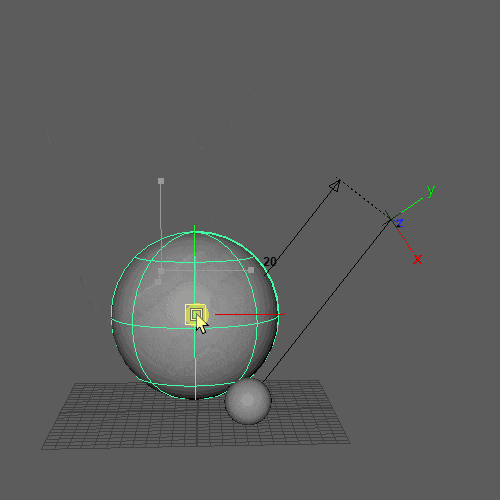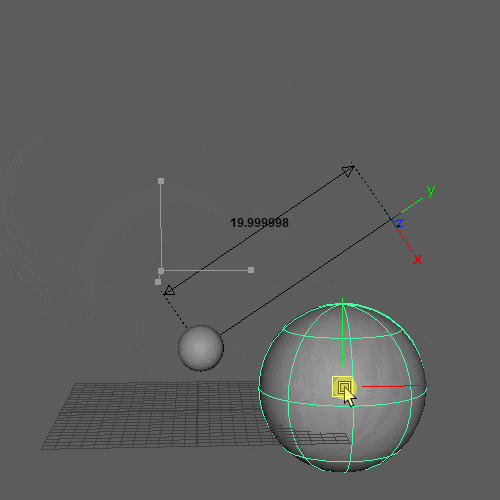
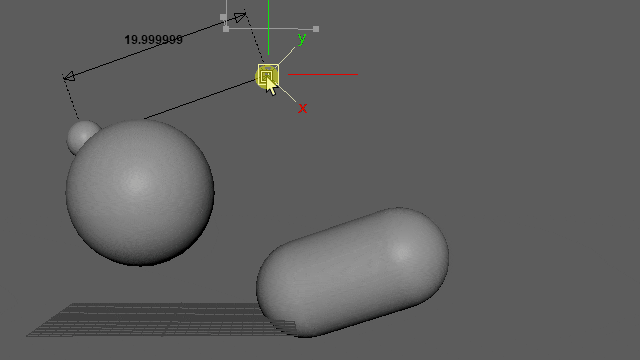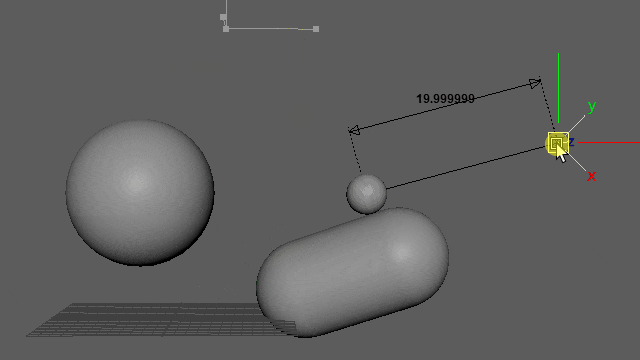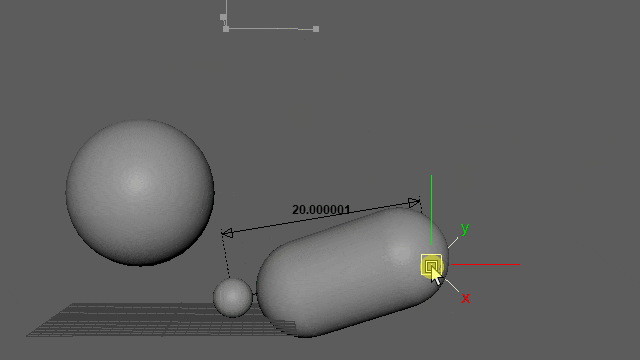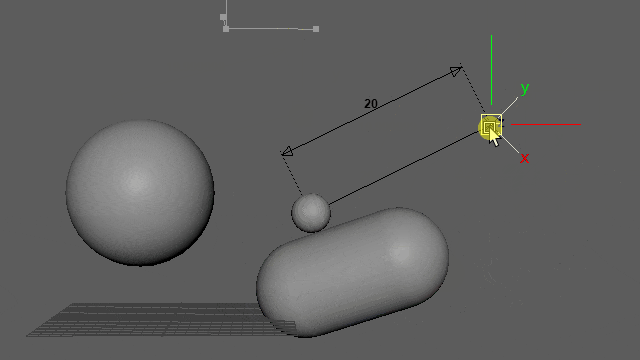
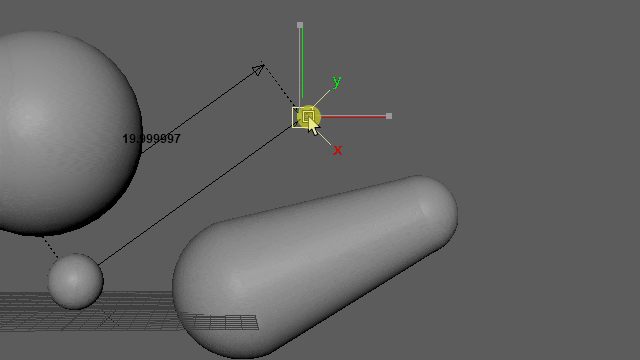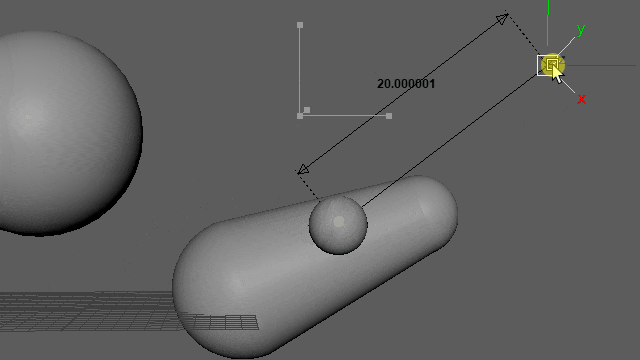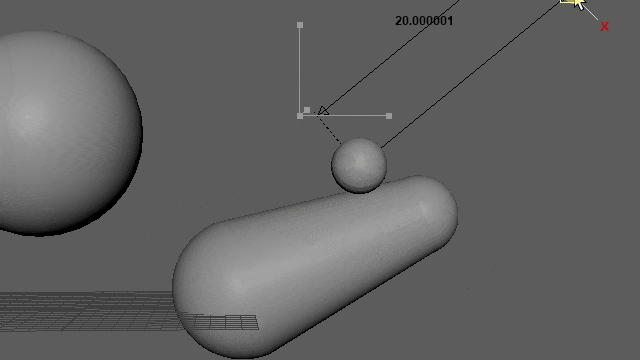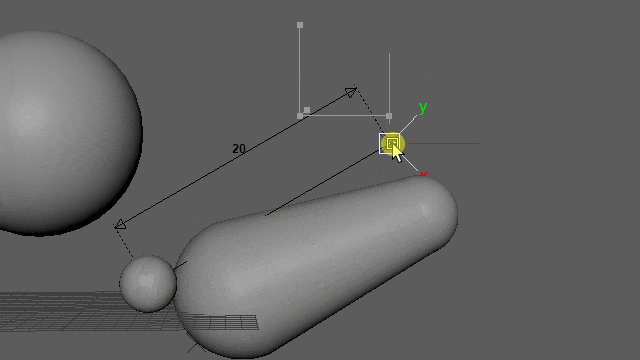
再生しなくても0フレ(Resetされるフレーム)以外であればマニピュレーター操作で動きを確認できます。
カプセル
参考リンクはこちら。こちらも最低限の説明でいきます。
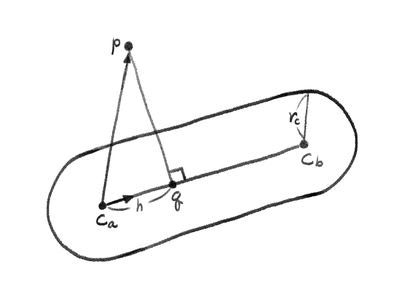
カプセル両端の球の中心を$c_a, c_b$として、まず$p$から線分$c_ac_b$への最近傍点$q$を求めたいのですが、先に$c_a,q$間の距離$h$を出します。
h = \frac{c_b-c_a}{\|c_b-c_a\|} \cdot (p-c_a)
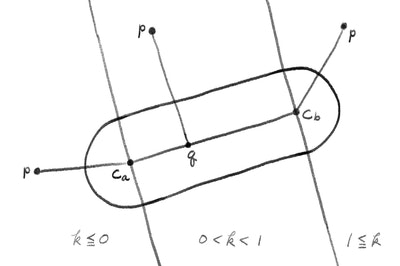
$h$を$c_a, c_b$間の距離$d_c$で割った値を見ると$p$がどの領域にあるかが分かります。
\displaylines{
k = \frac{h}{d_c} \\
\begin{cases}
k \leqq 0 \\
1 \leqq k \\
0 < k < 1
\end{cases}
}
$k$が0以下の場合と1以上の場合は球の時と同じです。$k$が0~1の間の場合は次の式で衝突判定を行います。$r_c$はカプセルの半径です。
\displaylines{
q = c_a + \frac{c_b-c_a}{\|c_b-c_a\|} h \\\
(p-q) \cdot (p-q) < (r_c+r_p)^2
}
衝突していたら、$q$から$qp$方向に向かって$r_c + r_p$だけ離れた位置に$p$を修正します。
p' = q + \frac{p-q}{\|p-q\|} (r_c + r_p)
Bifrostグラフは次のようになります。
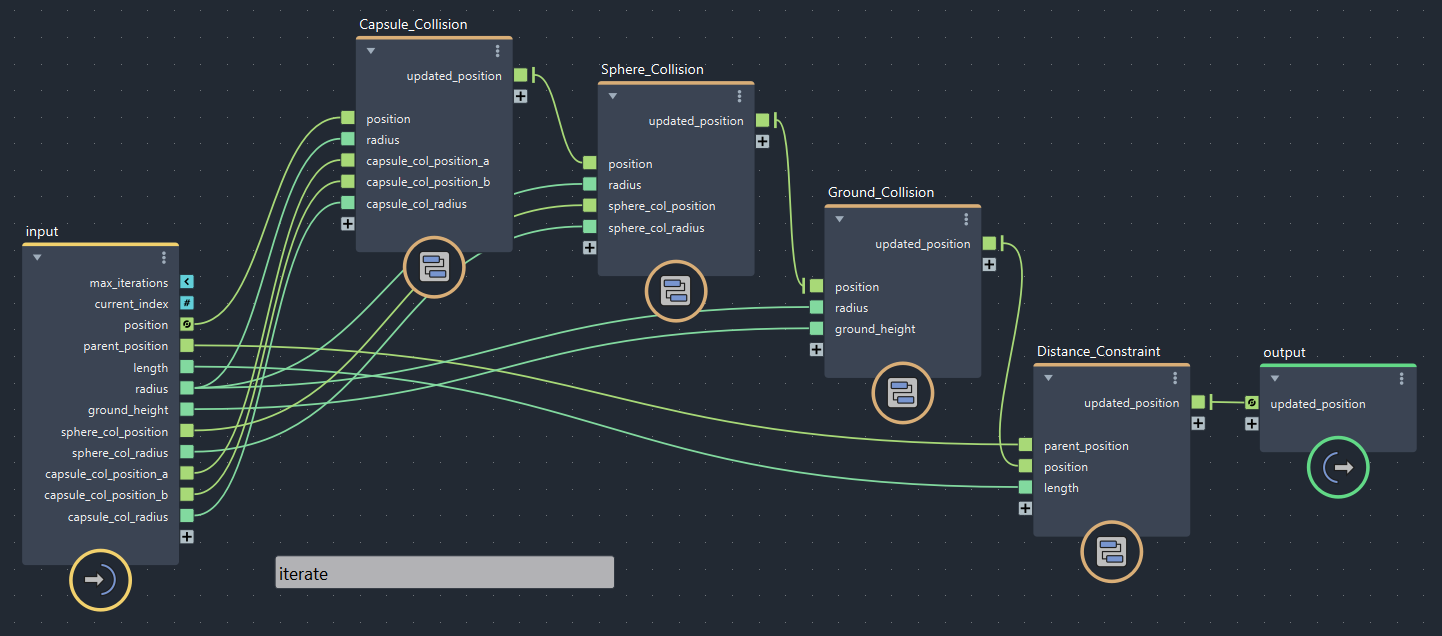
▲bifrostGraphShape > pbd > iterate
ちょっとグラフの威圧感が強めになってきましたね…。右上のほうで、先ほど作った球コリジョンも使われてます。
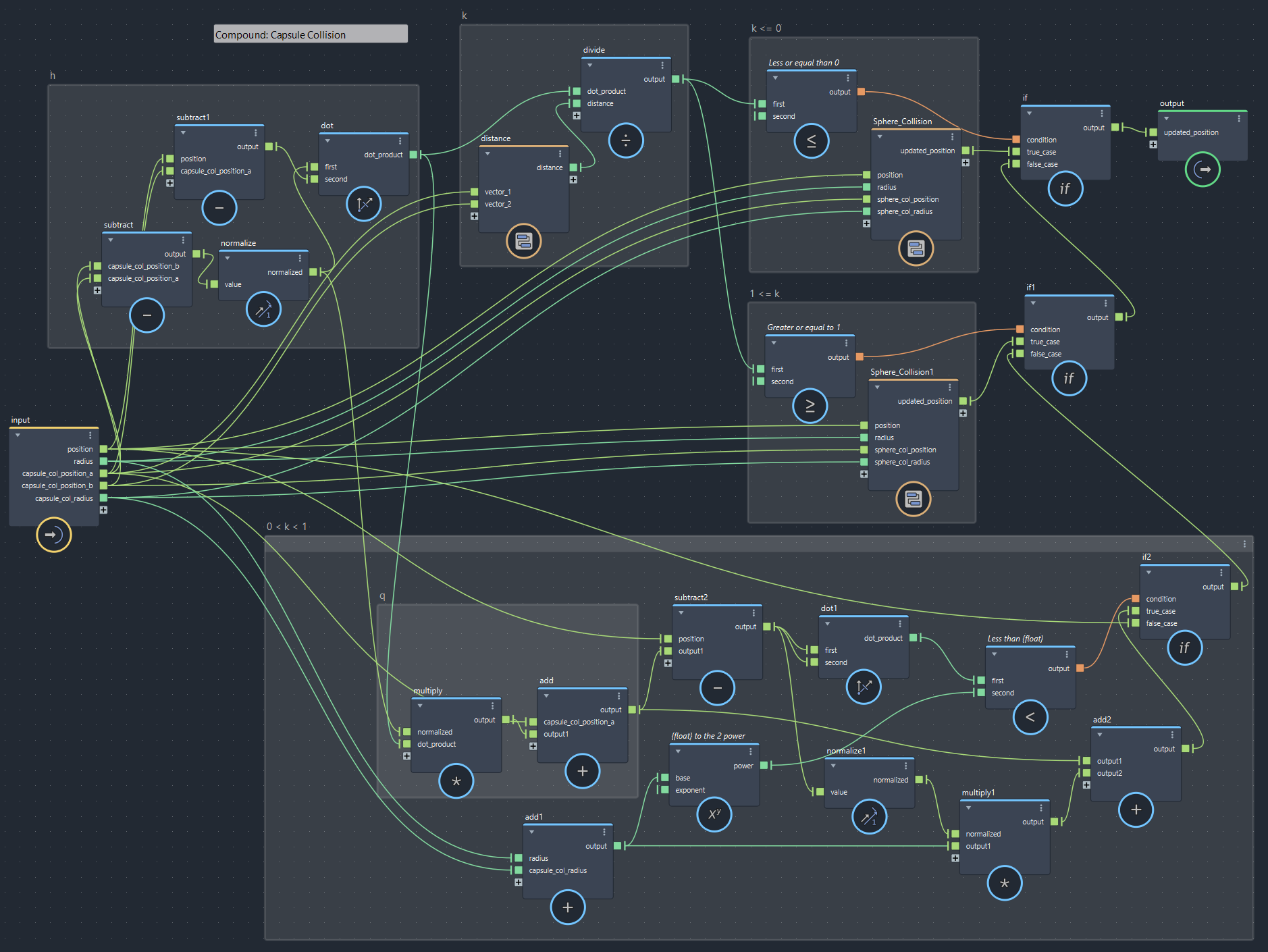
▲bifrostGraphShape > pbd > iterate > Capsule_Collision
ちなみに、先ほどの$k$は$q$がカプセル上のどの位置にいるかの割合です。もしカプセル両端の球の半径が違っていてそれぞれ$r_{ca}, r_{cb}$の場合、これらを$k$で補間すれば$q$地点での半径が出ます。
(1-k)r_{ca} + kr_{cb}
Bifrostグラフはこのようになります。
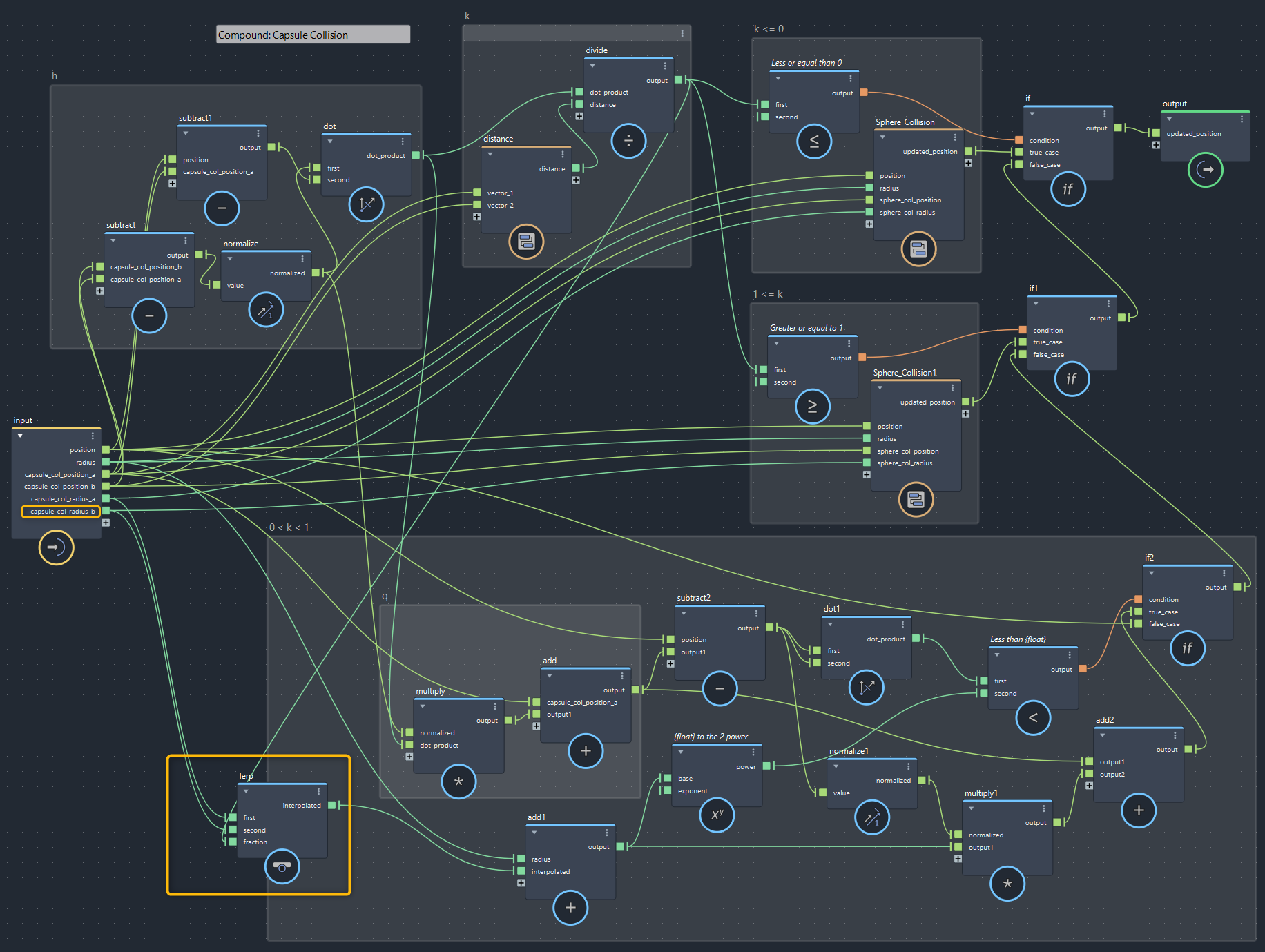
▲bifrostGraphShape > pbd > iterate > Capsule_Collision(変わっているのは黄色枠の部分です)
カプセル型のプリミティブはMayaにないのでこちらのスクリプトを使ってみて下さい。ちょうどいい具合のカプセルコライダーが生成されます。
from maya import cmds
root = cmds.createNode('transform', n='capsuleCollider')
cmds.addAttr(root, ln='radiusA', nn='Radius A', at='double', dv=0.5, min=0.001, k=True)
cmds.addAttr(root, ln='radiusB', nn='Radius B', at='double', dv=0.5, min=0.001, k=True)
cmds.addAttr(root, ln='height', nn='Height', at='double', dv=2.0, min=0.001, k=True)
sphere1 = cmds.sphere(ssw=180, esw=360, nsp=8, ax=[1,0,0])
sphere2 = cmds.sphere(ssw=0, esw=180, nsp=8, ax=[1,0,0])
circle1 = cmds.circle(s=16, nr=[0,1,0])
circle2 = cmds.circle(s=16, nr=[0,1,0])
loftedSurface = cmds.loft(circle1[0], circle2[0])
cmds.parent(sphere1[0], root, r=1)
cmds.parent(sphere2[0], root, r=1)
cmds.parent(circle1[0], root, r=1)
cmds.parent(circle2[0], root, r=1)
cmds.parent(loftedSurface[0], root, r=1)
cmds.setAttr(circle1[0] + '.v', 0)
cmds.setAttr(circle2[0] + '.v', 0)
md1 = cmds.createNode('multiplyDivide')
md2 = cmds.createNode('multiplyDivide')
cmds.setAttr(md1 + ".operation", 1)
cmds.setAttr(md1 + ".input2X", 0.5)
cmds.setAttr(md2 + ".operation", 1)
cmds.setAttr(md2 + ".input2X", -0.5)
cmds.connectAttr(root + '.worldInverseMatrix[0]', loftedSurface[0] + '.offsetParentMatrix', f=True)
cmds.connectAttr(md1 + '.outputX', sphere1[0] + '.ty', f=True)
cmds.connectAttr(md2 + '.outputX', sphere2[0] + '.ty', f=True)
cmds.connectAttr(md1 + '.outputX', circle1[0] + '.ty', f=True)
cmds.connectAttr(md2 + '.outputX', circle2[0] + '.ty', f=True)
cmds.connectAttr(root + '.height', md1 + '.input1X', f=True)
cmds.connectAttr(root + '.height', md2 + '.input1X', f=True)
cmds.connectAttr(root + '.radiusA', sphere1[1] + '.radius', f=True)
cmds.connectAttr(root + '.radiusB', sphere2[1] + '.radius', f=True)
cmds.connectAttr(root + '.radiusA', circle1[1] + '.radius', f=True)
cmds.connectAttr(root + '.radiusB', circle2[1] + '.radius', f=True)
無限平面
参考リンクはこちら。「ある点から平面までの距離」のところです。同じく説明は最低限でいきます。
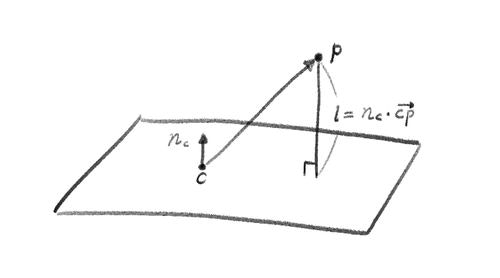
平面上の点を$c$、平面の法線を$n_c$として、$p$から平面までの最短距離$l$を出します。この距離がマイナス値になっていたら、衝突しています。
\displaylines{
l = n_c \cdot (p-c) \\\
l - r_p < 0
}
このとき、$n_c$方向に向かって埋まった距離分だけ$p$を移動します。
p' = p + n_c |l-r_p|
Bifrostグラフは次のようになります。
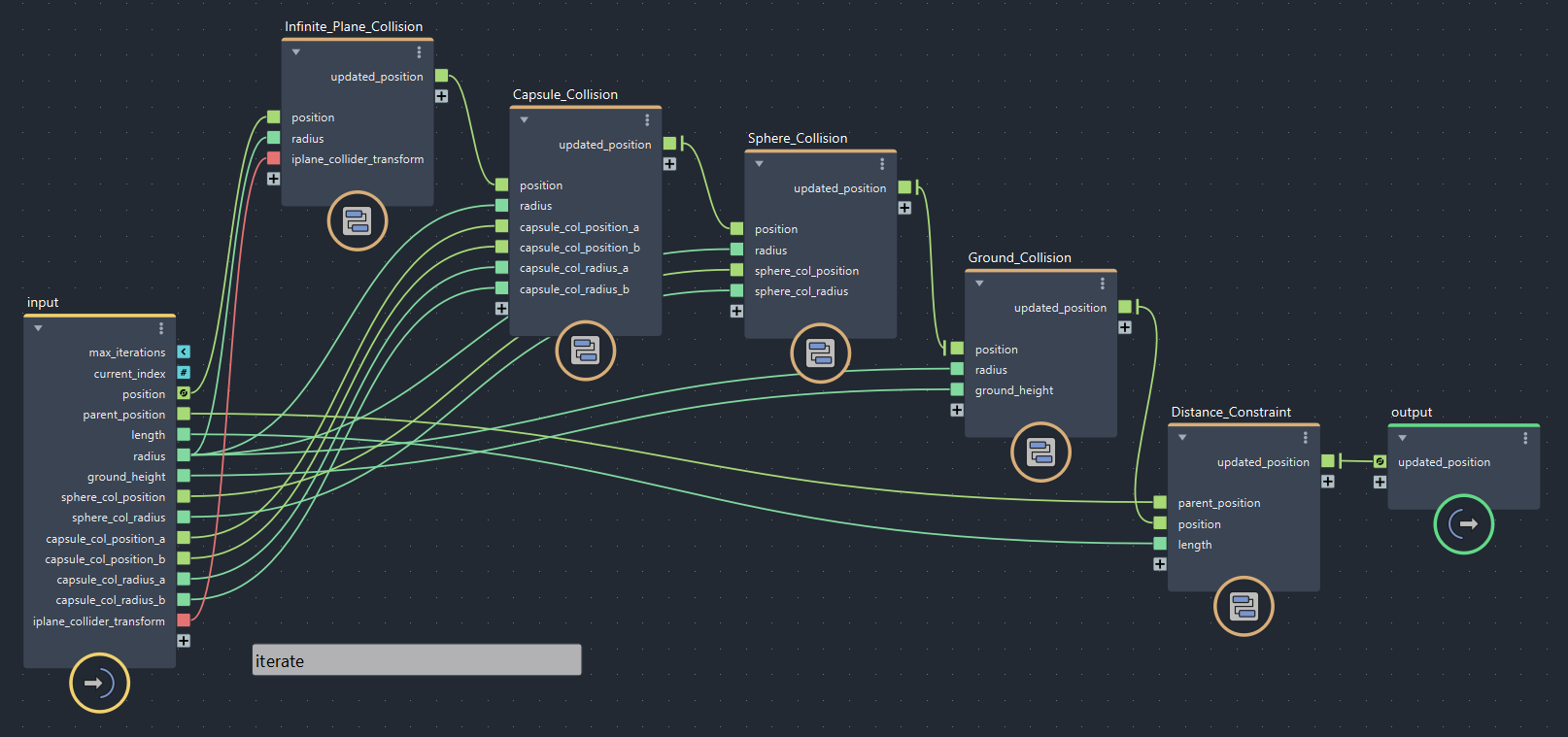
▲bifrostGraphShape > pbd > iterate
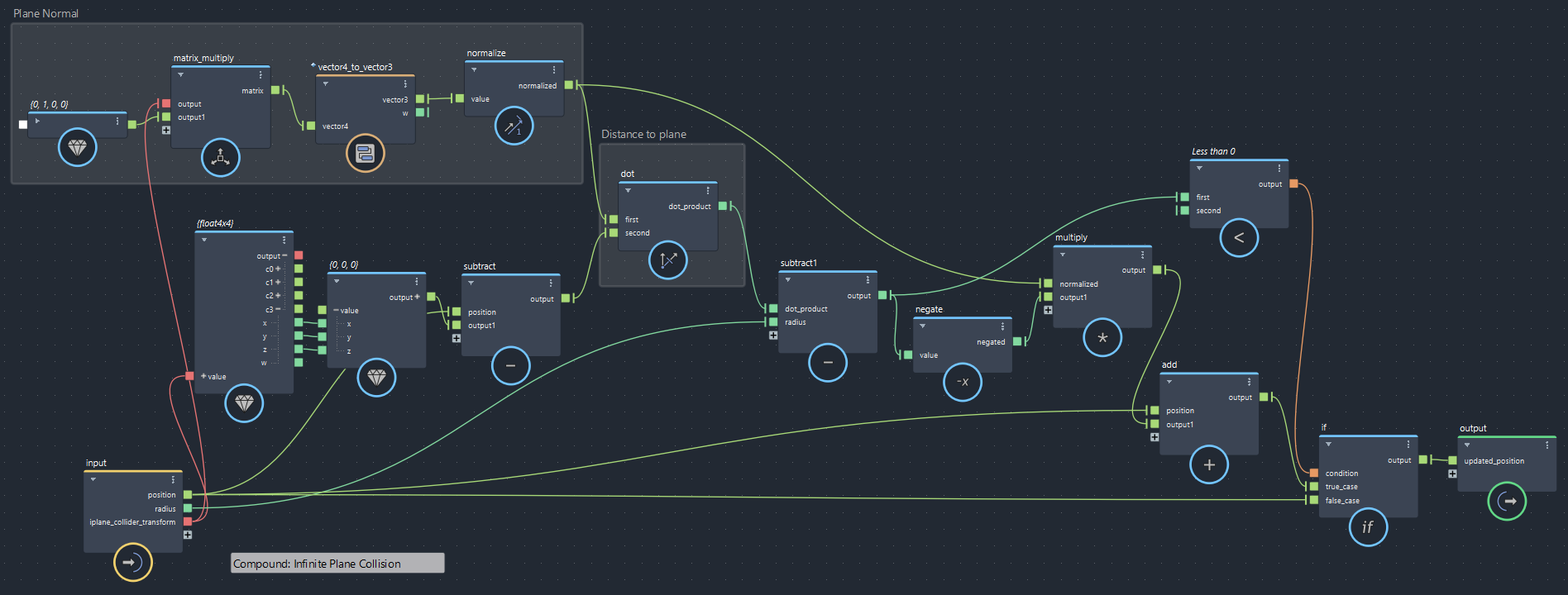
▲bifrostGraphShape > pbd > iterate > Infinite_Plane_Collision
プリミティブのみとはいえコリジョンが入るとだいぶワクワク感が増してきたかと思います!次回はついに、第1回冒頭にチラ見せしたようなぷるぷるゼリーやロープを作ってみます。
今回のグラフまとめ
地面コリジョン(bifrostGraphShape > pbd > iterate > Ground_Collision)

球コリジョン(bifrostGraphShape > pbd > iterate > Sphere_Collision)

カプセルコリジョン:半径共有(bifrostGraphShape > pbd > iterate > Capsule_Collision)

カプセルコリジョン:半径個別(bifrostGraphShape > pbd > iterate > Capsule_Collision)

無限平面コリジョン(bifrostGraphShape > pbd > iterate > Infinite_Plane_Collision)

制約のイテレーション例(bifrostGraphShape > pbd > iterate)

前の記事
次の記事