はじめに
弊社では、自然言語処理技術を使ったシステム開発を行なっていますが、自然言語処理技術の中の1つにBERTがあります。
以前、BERTの単語ベクトルに関するを書きましたが、その原理についてはよく理解してませんでした。
BERTの単語ベクトルを覗いてみる
BERTの単語ベクトルをさらに覗いてみる
色々と調べてみたところ、Transformer、Attentionというキーワードに行き当たりましたが、これがまたよくわからない代物でした。
ただし、
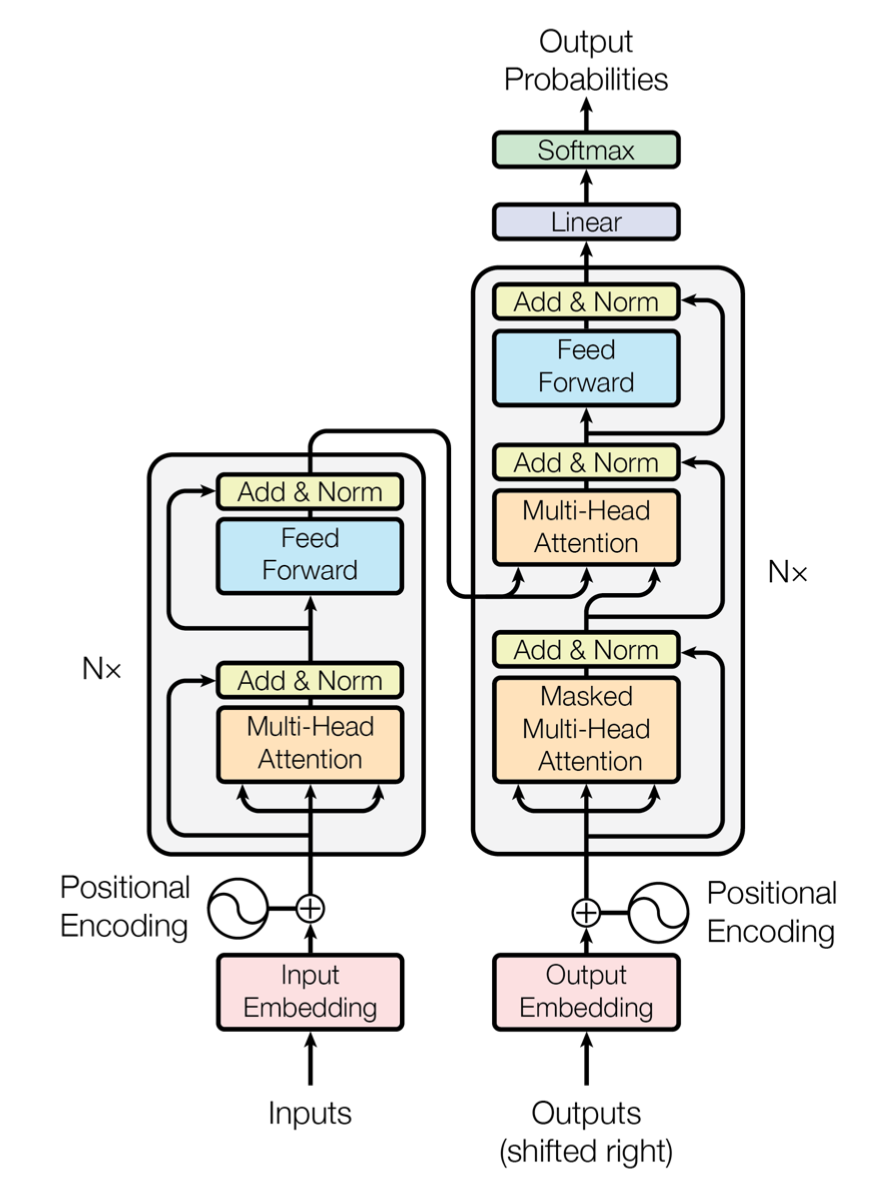
・BERTにはTransformerのencoder部分が使われている
・Transformerの肝はAttention(Self-Attention)である
ということがわかったので、まずはSelf-Attentionの理解を試みました。
まだ完全には理解できてませんが、何となくイメージをすることができたので、ざっくりと解説します。
なお、話を単純にするために、正確なSelf-Attentionの説明ではありませんが、イメージは間違ってないと思います。
Self-Attentionとは?
かなりシンプルに説明すると、Self-Attentionとは、文脈を考慮して単語をベクトル化する技術です。
自然言語処理では、単語をベクトル化する必要があります。
例えば、「りんごのapple、iPhoneのapple。」という文を例に考えていきます。
Word2Vecなどを使うと、この文内の単語をベクトルにすることができます(以降、このベクトルを「埋め込みベクトル」と表現します)。
ここから先は、Word2Vecで「りんご」、1番目の「apple」、「iPhone」、2番目の「apple」の4つの単語が、それぞれ以下のような4つの埋め込みベクトルに変換されたとして話を続けます。
・$りんご=\boldsymbol{x_{りんご}}$
・$apple(1番目)=\boldsymbol{x_{apple1}}$
・$iPhone=\boldsymbol{x_{iPhone}}$
・$apple(2番目)=\boldsymbol{x_{apple2}}$
Word2Vecでは単語の意味を区別できないため、1番目の「apple」に対する埋め込みベクトルと、2番目の「apple」に対する埋め込みベクトルとは同じ値となります。
Self-Attentionでは、Word2Vecなどで事前に埋め込みベクトル化された文内の全ての単語の重み付き和として、各単語を表します(正確にはベクトル $x_{*}$ はそのままではなく$x_{*}$に行列$W_v$をかけたベクトル$v_{*}=W_v x_{*}$を使いますが、イメージしやすいように$x_{*}$のまま説明します)。
・$りんご=0.8\boldsymbol{x_{りんご}}+0.3\boldsymbol{x_{apple1}}+0.01\boldsymbol{x_{iPhone}}+0.1\boldsymbol{x_{apple2}}$
・$apple(1番目)=0.4\boldsymbol{x_{りんご}}+0.9\boldsymbol{x_{apple1}}+0.05\boldsymbol{x_{iPhone}}+0.2\boldsymbol{x_{apple2}}$
・$iPhone=0.1\boldsymbol{x_{りんご}}+0.02\boldsymbol{x_{apple1}}+0.88\boldsymbol{x_{iPhone}}+0.39\boldsymbol{x_{apple2}}$
・$apple(2番目)=0.05\boldsymbol{x_{りんご}}+0.2\boldsymbol{x_{apple1}}+0.4\boldsymbol{x_{iPhone}}+0.88\boldsymbol{x_{apple2}}$
各埋め込みベクトルの前についている係数は、「Attention係数」と呼ばれるもので、その単語ベクトルを構成する各埋め込みベクトルのうち、どれに注目すべきかの度合いを表しています(例のため正確な値ではありません)。
例えば「apple(1番目)」の場合、自分自身を表す$\boldsymbol{x_{apple1}}$の係数が一番大きく、意味の近い$\boldsymbol{x_{りんご}}$の係数も大きな値となっています。
このように、Self-Attentionでは文内のすべての単語の情報を使って単語をベクトル化するため、単語ベクトル内に文脈を表現することができると考えられています。
Self-Attentionの求め方
先ほど、ある単語から見て、文内のどの単語に注目すべきかの度合いを表す「Attention係数」というものを紹介しましたが、この係数はどのように求めるのでしょうか?
ここからは、その方法について説明します(先述した通り、イメージしやすいように単純化してあります)。
まず、記号の説明です。
単語1から単語2へのAttenttion係数(単語1から見た時の単語2の注目の度合い)を$a_{単語1,単語2}$と書くことにします。
こうすると、各単語のベクトルは次のようになります。
・$りんご=a_{りんご,りんご}\boldsymbol{x_{りんご}}+a_{りんご,apple1}\boldsymbol{x_{apple1}}+a_{りんご,iPhone}\boldsymbol{x_{iPhone}}+a_{りんご,apple2}\boldsymbol{x_{apple2}}$
・$apple(1番目)=a_{apple1,りんご}\boldsymbol{x_{りんご}}+a_{apple1,apple1}\boldsymbol{x_{apple1}}+a_{apple1,iPhone}\boldsymbol{x_{iPhone}}+a_{apple1,apple2}\boldsymbol{x_{apple2}}$
・$iPhone=a_{iPhone,りんご}\boldsymbol{x_{りんご}}+a_{iPhone,apple1}\boldsymbol{x_{apple1}}+a_{iPhone,iPhone}\boldsymbol{x_{iPhone}}+a_{iPhone,apple2}\boldsymbol{x_{apple2}}$
・$apple(2番目)=a_{apple2,りんご}\boldsymbol{x_{りんご}}+a_{apple2,apple1}\boldsymbol{x_{apple1}}+a_{apple2,iPhone}\boldsymbol{x_{iPhone}}+a_{apple2,apple2}\boldsymbol{x_{apple2}}$
Attention係数 $a_{単語1,単語2}$は、埋め込みベクトル $\boldsymbol{x_{単語1}}$と埋め込みベクトル $\boldsymbol{x_{単語2}}$との内積を計算することで求まります(正確には、$W_q\boldsymbol{x_{単語1}}$と$W_k\boldsymbol{x_{単語2}}$との内積)。
$$
a_{単語1,単語2} = \boldsymbol{x_{単語1}} \cdot \boldsymbol{x_{単語2}}
$$
ここで重要なのは次の点です。
Word2Vecなどで生成した埋め込みベクトルの内積は単語の類似度を表している。
すなわち類似した単語同士の内積ほど大きな値となる。
このことから、「apple(1番目)」のベクトルの場合で考えると、Attention係数$a_{apple1,apple1}$、$a_{apple1,りんご}$が大きな値となり、$\boldsymbol{x_{apple1}}$、$\boldsymbol{x_{りんご}}$の影響が大きくなるのです。
非常にシンプルな仕組みですが、よくできています。
ちなみに、実際に計算する際には、Attention係数を集めてできるAttention行列$A$と、埋め込みベクトルを集めてできる文行列$X$との行列積で計算できるため、GPUのパワーを活用することができます。これがTransformerの利点です。
$$
AX =
\begin{bmatrix}
a_{りんご,りんご} & a_{りんご,apple1} & a_{りんご,iPhone} & a_{りんご,apple2} \
a_{apple1,りんご} & a_{apple1,apple1} & a_{apple1,iPhone} &a_{apple1,apple2} \\
a_{iPhone,りんご} & a_{iPhone,apple1} & a_{iPhone,iPhone} &a_{iPhone,apple2} \\
a_{apple2,りんご} & a_{apple2,apple1} & a_{apple2,iPhone} &a_{apple2,apple2} \\
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{x_{りんご}} \
\boldsymbol{x_{apple1}} \
\boldsymbol{x_{iPhone}} \
\boldsymbol{x_{apple2}} \
\end{bmatrix}
$$
単語の位置情報
「Self-Attentionとは」の中で、このように書きました。
Word2Vecでは単語の意味を区別できないため、1番目の「apple」に対する埋め込みベクトルと、2番目の「apple」に対する埋め込みベクトルとは同じ値となります。
ここまで「apple(1番目)」、「apple(2番目)」の埋め込みベクトルをそれぞれ$\boldsymbol{
x_{apple1}}$、$\boldsymbol{x_{apple2}}$と書いて区別をしていましたが、実はこれらは同じ値なのです。そこでこれらを$\boldsymbol{x_{apple}}$と書きなおすと、Self-Attentionで得られる「apple(1番目)」、「apple(2番目)」に対するベクトルは、次のように書き換えられます。
・$apple(1番目)=a_{apple,りんご}\boldsymbol{x_{りんご}}+a_{apple,apple}\boldsymbol{x_{apple}}+a_{apple,iPhone}\boldsymbol{x_{iPhone}}+a_{apple,apple}\boldsymbol{x_{apple}}$
・$apple(2番目)=a_{apple,りんご}\boldsymbol{x_{りんご}}+a_{apple,apple}\boldsymbol{x_{apple}}+a_{apple,iPhone}\boldsymbol{x_{iPhone}}+a_{apple,apple}\boldsymbol{x_{apple}}$
せっかく頑張ったのに、区別がつかなくなってしまいました。
Transformerでは、単語の位置情報(文内での単語の位置)を各埋め込みベクトルに足し合わせることで、「apple(1番目)」、「apple(2番目)」のような、同じ単語でも出現位置が異なるものを区別する工夫をしています。
興味のある方は、以下の記事が参考になると思います。
Transformer Architecture: The Positional Encoding
最後に
Web上にTransformer、Self-Attentionに関する素晴らしい記事が多くありますが、どれもそれを読むための前提知識が暗黙的に求められているため、それらを読んでも私には良く理解できませんでした。
そこで、この記事では正確な理解は犠牲にして、Self-Attentionが何となくイメージできるようになることを目的としています。
少しでもイメージができらた、正確な理解のために以下のTransformerの原論文を読むことをお勧めします。
Attention Is All You Need
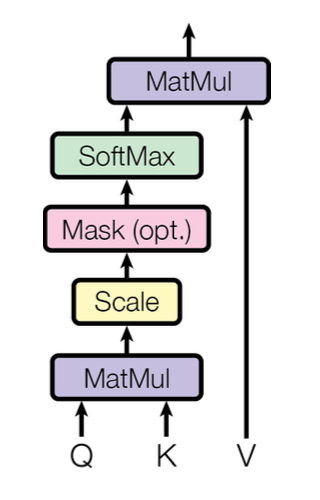
この記事では、埋め込みベクトル$\boldsymbol{x}$同士の内積でAttention係数を求め、Attention係数を埋め込みベクトル$\boldsymbol{x}$にかけて各単語のベクトルを計算しましたが、実際には、埋め込みベクトル$\boldsymbol{x}$を変換してできるquery、keyと呼ばれるベクトル同士の内積でAttention係数を求め、それを埋め込みベクトル$\boldsymbol{x}$を変換してできるvalueと呼ばれるベクトルにかけて各単語のベクトルを計算します。
上記の論文を読む際には、このイメージを持って読むと理解がしやすいと思います。