概要
画像集合をもとに新しい視点からの画像を合成する技術の一つである。
NeRFとは異なり、鏡面物体とその映り込み風景を再現することができる。
しかし、半透明な物体を表現できないという短所を持っている。
書誌情報
- Zhang, Kai, et al. "Physg: Inverse rendering with spherical gaussians for physics-based material editing and relighting." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.
- https://openaccess.thecvf.com/content/CVPR2021/html/Zhang_PhySG_Inverse_Rendering_With_Spherical_Gaussians_for_Physics-Based_Material_Editing_CVPR_2021_paper.html
- 公式プロジェクトページ
モデル概要
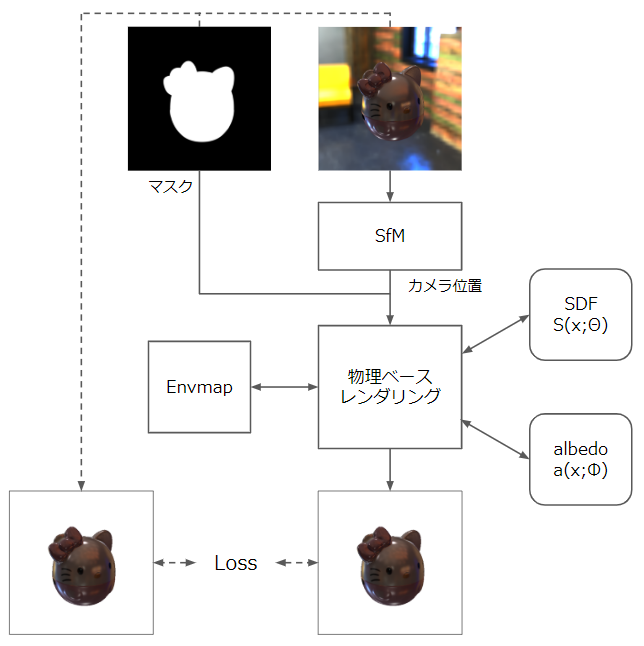
以下の図がモデルの概要を示した図である。
補足としてそれぞれのモジュールの基本的な動作も下に記す。
| 名称 | 主な役割 | 入力 | 出力 |
|---|---|---|---|
| SfM | オブジェクトとカメラの位置関係を算出 | オブジェクトを撮影した画像 | カメラの座標,方向 |
| SDF | オブジェクトの形状を表現 | 座標 | 最も近いオブジェクトの面の座標 |
| albedo | オブジェクトの色を表現 | 座標 | 与えられた座標のオブジェクトの色 |
| Envmap | 映りこんでいる周辺の風景 | 方向ベクトル | 与えられた方向からオブジェクトに向かって飛ぶ光の色 |
| 物理ベースレンダリング | 与えられた座標とオブジェクトの情報からレンダリングを行う | カメラの位置,SDF,albedo,Envmap | 画像 |
具体的な説明
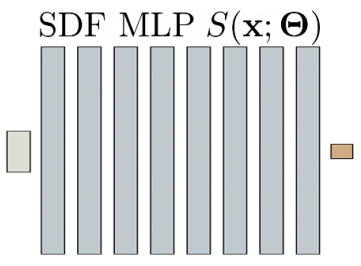
SDF
$S(x; Θ)$
SDFは球を表現するように初期化する
構成
MLP
- 8層の512次元の非線形層
- 4層目にskip connection
- 3次元点の位置を6つの周波数成分で符号化するpositional encoding
なお法線ベクトル$n$を算出するのに利用でき、$n=∇_xS(x; Θ)$で算出可能
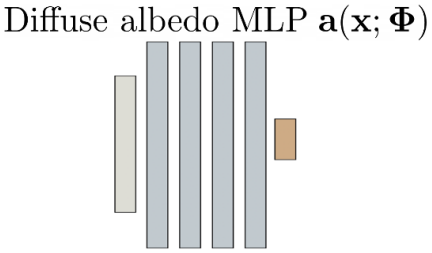
albedo(拡散アルベド)
$a(x; Φ)$
構成
MLP
- 4層の512次元の非線形層
- 3次元点の位置を10の周波数成分で符号化するpositional encoding
Loss Function
以下のように誤差関数を定義する
- 1項目
オブジェクトの像が存在しているピクセル(マスクがかかっていないピクセル)は、実際の画像のそのピクセルの色と比較し、その誤差の1ノルムをノルムをロスとする。 - 2項目
マスクからオブジェクトの形を矯正するために、マスクのかかっているオブジェクトの像がないないピクセルのレイから計算されるSDFの値に応じてロスを定義し、これが正の値になるように矯正する。 - 3項目
SDFは面からの距離を表すものなので、座標が1変われば値も1変わる必要がある。なのでそうなるように調整する。
\begin{aligned}
\ell=& \frac{1}{N_{o b j}} \sum_{i=1}^{N_{o b j}}\left\|\mathbf{c}_{i}^{o b j}-\mathbf{c}_{i}^{g t}\right\|_{1} \\
&+\beta_{1} \frac{1}{N_{n o b j}} \sum_{i=1}^{N_{n o b j}} \frac{\ln \left(1+e^{-\alpha S_{i}^{n o b j}}\right)}{\alpha} \\
&+\beta_{2} \frac{1}{N_{x}} \sum_{i=1}^{N_{x}}\|\| \nabla_{\mathbf{x}_{i}} S\left\|_{2}-1\right\|_{2}^{2}
\end{aligned}
物理ベースレンダリング
NeRFの場合ボリュームレンダリングという微分可能なレンダリングの手段がとられている。
ここではそれの代替として物理ベースレンダリングというものを用いる。
大まかに計算過程を順に記述すると以下のようになる。
カメラの任意のピクセルに入ってくる光の色を計算する。
1 球面ガウス関数を定義する 今後これをいくつかの場面で活用する
G(\boldsymbol{\nu} ; \boldsymbol{\xi}, \lambda, \boldsymbol{\mu})=\boldsymbol{\mu} e^{\lambda(\boldsymbol{\nu} \cdot \boldsymbol{\xi}-1)}
2 物体上で特定の方向$ω_i$から飛んでくる光を算出する $\mathbf{ξ_n},\mathbf{λ_n},\mathbf{μ_n}$はEnvmapに保存されているパラメータである($M=128$)
L_{i}\left(\boldsymbol{\omega}_{i}\right)=\sum_{k=1}^{M} G\left(\boldsymbol{\omega}_{i} ; \boldsymbol{\xi}_{k}, \lambda_{k}, \boldsymbol{\mu}_{k}\right)
3 物体の複雑な反射特性(特定の方向にどのくらい反射するかの特性)を近似的に再現するために以下の複数の式を定義する $R,\mathbf{s}$は反射特性を示すパラメータでありこれは定数で任意の値で初期化する。
\mathbf{h}=\frac{\boldsymbol{\omega}_{o}+\boldsymbol{\omega}_{i}}{\left\|\boldsymbol{\omega}_{o}+\boldsymbol{\omega}_{i}\right\|_{2}}
k=\frac{(R+1)^{2}}{8}
\mathcal{F}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i}\right)=\boldsymbol{s}+(1-\boldsymbol{s}) \cdot 2^{-\left(5.55473 \boldsymbol{\omega}_{o} \cdot \mathbf{h}+6.8316\right)\left(\boldsymbol{\omega}_{o} \cdot \mathbf{h}\right)}
\mathcal{G}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i}\right)=\frac{\boldsymbol{\omega}_{o} \cdot \mathbf{n}}{\boldsymbol{\omega}_{o} \cdot \mathbf{n}(1-k)+k} \cdot \frac{\boldsymbol{\omega}_{i} \cdot \mathbf{n}}{\boldsymbol{\omega}_{i} \cdot \mathbf{n}(1-k)+k}
\mathcal{M}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i}\right)=\frac{\mathcal{F}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i}\right) \mathcal{G}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i}\right)}{4\left(\mathbf{n} \cdot \boldsymbol{\omega}_{o}\right)\left(\mathbf{n} \cdot \boldsymbol{\omega}_{i}\right)}
\mathcal{D}(\mathbf{h})=G\left(\mathbf{h} ; \mathbf{n}, \frac{2}{R^{4}}, \frac{1}{\pi R^{4}}\right)
f_{s}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i}\right)=\mathcal{M}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i}\right) \mathcal{D}(\mathbf{h})
4 オブジェクトの表面が吸収する光(albedo)を定義する
f_{r}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i} ; \mathbf{x}\right)=\frac{\mathbf{a}}{\pi}+f_{s}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i} ; \mathbf{x}\right)
5 反射が発生する座標、反射特性、入射光などを統合しカメラの任意のピクセルに向かう光の色を算出
L_{o}\left(\boldsymbol{\omega}_{o} ; \mathbf{x}\right)=\int_{\Omega} L_{i}\left(\boldsymbol{\omega}_{i}\right) f_{r}\left(\boldsymbol{\omega}_{o}, \boldsymbol{\omega}_{i} ; \mathbf{x}\right)\left(\boldsymbol{\omega}_{i} \cdot \mathbf{n}\right) \mathrm{d} \boldsymbol{\omega}_{i}
なお、カメラのレイとオブジェクトの交差点(反射点)の座標はスフィアトレーシングという手法でSDFを利用しながら計算される。
この項目において参考になる関連記事
物理ベースレンダリングを柔らかく説明してみる(1)
物理ベースレンダリングを柔らかく説明してみる(2)
物理ベースレンダリングを柔らかく説明してみる(3)
基礎からはじめる物理ベースレンダリング(Zenn)
GLSL: シェーダ内でレイを定義する - wgld.org