LoginSignup
0
3
@Yushin-Tati

Python初心者の備忘録 #11 ~統計学入門編01~

Last updated at Posted at 2024-02-27

はじめに

今回私は最近はやりのchatGPTに興味を持ち、深層学習について学んでみたいと思い立ちました！
深層学習といえばPythonということなので、最終的にはPythonを使って深層学習ができるとこまでコツコツと学習していくことにしました。
ただ、勉強するだけではなく少しでもアウトプットをしようということで、備忘録として学習した内容をまとめていこうと思います。
この記事が少しでも誰かの糧になることを願っております！
※投稿主の環境はWindowsなのでMacの方は多少違う部分が出てくると思いますが、ご了承ください。
最初の記事：Python初心者の備忘録 #01
前の記事：Python初心者の備忘録 #10 ~DSに使われるライブラリ編05~
次の記事：Python初心者の備忘録 #12 ~統計学入門編02~

今回からPythonを使用した統計学についてまとめていきます。
本記事は基本的な記述統計についてまとめてあります。

本記事はDockerで環境構築を行っているので、環境構築がまだという方は下記記事を参考にして、環境構築をしてください。
Python初心者の備忘録 #06 ~DSに使われるライブラリ編01~

■学習に使用している資料

Udemy：米国データサイエンティストが教える統計学超入門講座【Pythonで実践】

■データの準備

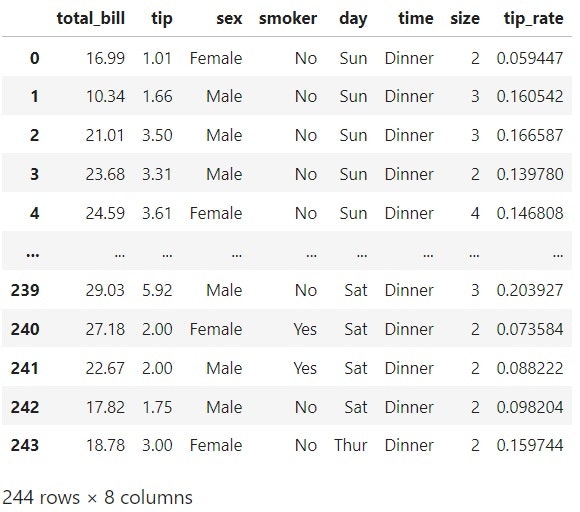
seabornというPythonのライブラリに既存で用意されているデータセットをloadして、今回の統計学の学習に使用する。
※サンプルデータについてはSeabornのGitHubを確認して下さい。

import seaborn as sns

# 今回はチップについてのデータを使用
df = sns.load_dataset('tips')

# tipsデータに'tip_rate'カラムを追加
df['tip_rate'] = df['tip'] / df['total_bill']

tips_dataframe.jpg

■記述統計

▶分布(distribution)

どの分野にどの程度のデータが存在するかを表したもの。
DataFrameのようにただの数値の集合では、そのデータの特性が見えないがグラフにしたとたん、ある程度推測できるようになる。
棒グラフ、ヒストグラム、円グラフなど...

・ヒストグラム(histgram)

  • 一つの連続変数の分布を表すのに使用される。(今回であれば、total_billやtipなど)
  • 棒のことをビン(bin)、件数のことを度数(frequency)という。
  • ある区間にどの程度の値が存在するか確認することができる。
  • 棒グラフと混同されるが、違うものなので注意。

sns.distplot(a)で描画可能で、aはデータarray。
※Seabornのバージョン(sns.__version__)が0.11.0以上の人はsns.displot(a)とする。
デフォルトではKDE(確率密度関数)が描画されるので、必要なければkde=Falseを引数に渡す。

# histgramの描画
sns.distplot(df['tip'], kde=False)

histgram.jpg

・棒グラフ(bar chart)

  • 棒を使ったグラフの総称
  • 1つのカテゴリ件数の分布をアラワクのに使用される。(今回であれば、sexやday、timeなど)
  • カテゴリごとの数値を確認することができる。

sns.catplot(x, data, kind)で描画可能で、xはカテゴリ変数、dataはカテゴリ変数を含むDataFrame、kindはどのように表示するかの指定。

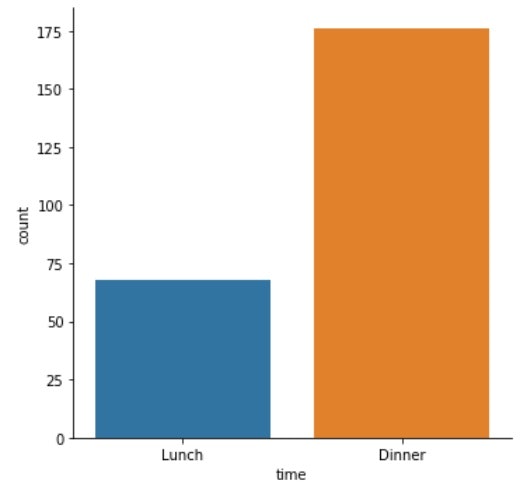
# 棒グラフ(カテゴリー)の描画
sns.catplot(x='time', data=df, kind='count')

category_bar_chart.jpg

▶記述統計と推測統計

記述統計は「データの特徴を記述する(例:平均値、中央値)」
推測統計は「標本から母集団の特徴を推測する(例:アンケート)」

統計学は基本的に推測統計の習得が目的となってくる。
population_sample.jpg

▶平均値(mean)

  • データの合計をデータの数で割った値(算術平均)
  • 通常、標本平均を$\bar{x}$、母集団平均をμで表す。
  • 平均の差(偏差(deviation))の合計は0になる。
  • 平均値は「各値からの差の2条の合計(平方和)」を最小にする。

次のような数式で表される
・$\bar{x}=\frac{x_1+x_2+…+x_n}{n}$

・$\bar{x}=\frac{1}{n}\sum_{i=1}^nx_i$

np.mean(data)やdf['column'].mean()で平均値を求めることができる。
df.groupby('category').mean()['column']でcategory毎のcolumnの平均値を出すことも可能。

sns.barplot(x, y, data)やdf.groupby('sex').mean()['tip_rate'].plot()で描画可能
sns.barplot()はデフォルトではエラーバーを表示するので、不要の場合は引数にci=Noneを指定する。

# 平均値
np.mean(df['tip_rate'])  # -> 0.16080258172250478
df['tip_rate'].mean()  # -> 0.16080258172250478

# カテゴリごとの平均値
df.groupby('sex').mean()['tip_rate']  # -> sex
                                      #    Male      0.157651
                                      #    Female    0.166491
                                      #    Name: tip_rate, dtype: float64

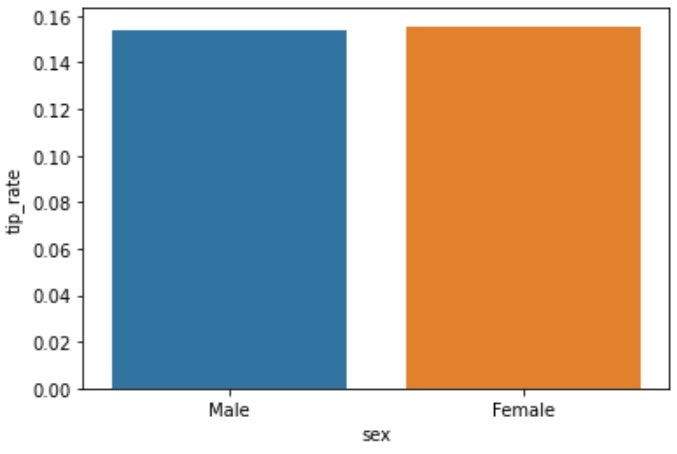
# 描画
sns.barplot(x='sex', y='tip_rate', data=df, ci=None)
# df.groupby('sex').mean()['tip_rate'].plot()でも描画可能

static_mean().jpg

▶中央値(median)

  • データを大きさ順に並べた際の真ん中の値
  • 平均値よりも外れ値の影響を受けにくい
  • 真ん中の値がない場合は、真ん中の二つの中間をとる
  • 平均値よりは計算に時間がかかってしまう(データのソートが必要なため)

np.median(data)やdf['column'].median()で中央値の算出が可能。
df.groupby('category').median('column')でカテゴリ毎の中央値を出力できる。

sns.barplot(x, y, data, estimate=np.median)で中央値の描画が可能

# 中央値
np.median(df['tip_rate'])
df['tip_rate'].median()

# カテゴリごとの中央値
df.groupby('sex').median()

# 描画
sns.barplot(x='sex', y='tip_rate', data=df, estimator=np.median, ci=None)

statistics_median().jpg

▶最頻値(mode)

  • データの中で最も多く観測される値(もっとも頻出)
  • 極端に特定の値に集中している場合は代表値として扱われるが、あまりない
  • 分布の山をモーダル(modal)と呼ぶ

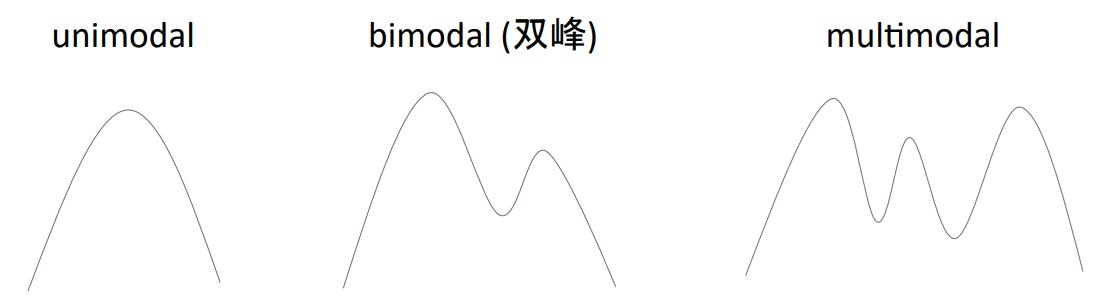
statistics_modal.jpg
stats.mode(data)やdf['column'].mode()で最頻値を出力可能。
statsを使用する場合はfrom scipy import statsでインポートする必要があり、返り値は最頻値リストとそのカウントのリストをタプルで返す。

df['column'].mode()は最頻値をseriesで返す。

# 最頻値
# ライブラリのimport
from syipy import stats

mode, count = stats.mode(df)
# 戻り値はリスト
print(mode)  # -> [[13.42 2.0 'Male' 'No' 'Sat' 'Dinner' 2 0.1448225923244026]]
print(count)  # -> [[  3  33 157 151  87 176 156   2]]

# Seriesでも可能
mode, count = stats.mode(df['size'])
print(mode, count)  # -> [2] [156]

# チップ率の最頻値は二つある(どちらとも2データある)
df['tip_rate'].mode()  # -> 0    0.144823
                       #    1    0.153846
                       #    dtype: float64

▶散布度

・範囲(range)

データの範囲、最大値～最小値。
外れ値に弱く、全体のばらつきを表すには不十分だったりする。

基本的に「最大値-最小値」で算出するので、Pythonでは最大値と最小値の算出方法を知っていればいい。

  • 最小値：np.min(data)やdf['column'].min()、df.groupby('column').min()
  • 最大値：np.max(data)やdf['column'].max()、df.groupby('column').max() 
# 最小値
np.min(data)
df['column'].min()
df.groupby('column').min()

# 最大値
np.max(data)
df['column'].max()
df.groupby('column').max()

# 範囲
max - min

・四分位数(quartile)

データを並べて4分割したときの25％、50％、75％の値でそれぞれ$Q_1$、$Q_2$、$Q_3$と表記される。
「範囲」よりは外れ値に強いが、散布度を示すにはまだ不十分。

  • $Q_3-Q_1$：四分位範囲(IQR：Interquartile range)
  • $\frac{IQR}{2}$：四分位偏差(QD：quartile deviation)

IQRを使用すると、最小値または最大値が外れ値だった場合でも、その値は使用しないことになるので、外れ値に強いということになる。
stats_quartile_IQR.jpg
np.quantile(data, [0.25,0.5,0.75])やde['column'].quantile([0.25,0.5,0.75])で四分位数を算出することができる。

stats.iqr(data)でIQRを求めることができる。

# 四分位数
np.quantile(df['tip_rate'], [0.25, 0.5, 0.75])  # -> array([0.12912736, 0.15476977, 0.19147549])
df['tip_rate'].quantile([0.25, 0.5, 0.75])  # -> 0.25    0.129127
                                            #    0.50    0.154770
                                            #    0.75    0.191475
                                            #    Name: tip_rate, dtype: float64

# IQR：四分位範囲
stats.iqr(df['tip_rate'])  # -> 0.06234812458689151

# QD：四分位偏差(IQR/2)
stats.iqr(df['tip_rate']) / 2  # -> 0.031174062293445756

・箱ひげ図(boxplot)

四分位数を使用してプロットされたグラフ。
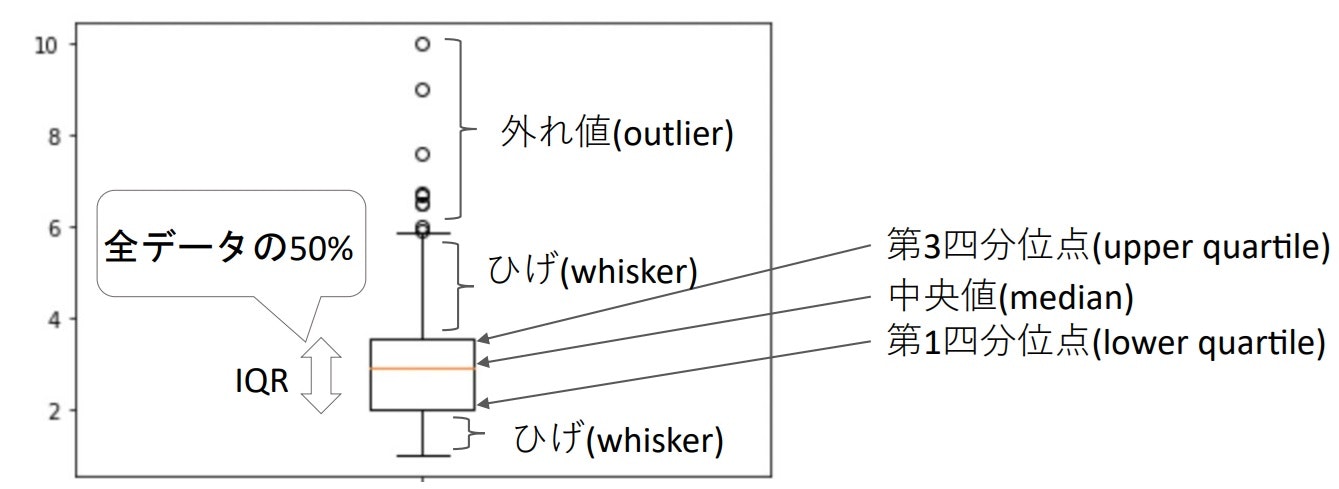
stats_boxplot.jpg
plt.boxplot(data)やsns.boxplot(data)で描画することができる。
sns.boxplot(x='category', y='column', data=df)とすることで、カテゴリごとの箱ひげ図を描画することも可能。

デフォルトでは「ひげ」は$Q_1$、$Q_3$からそれぞれIQR * 1.5の範囲で表示され、それ以上のデータは外れ値として扱われる。

# plt(matplotlib)のimport
import matplotlib.pyplot as plt

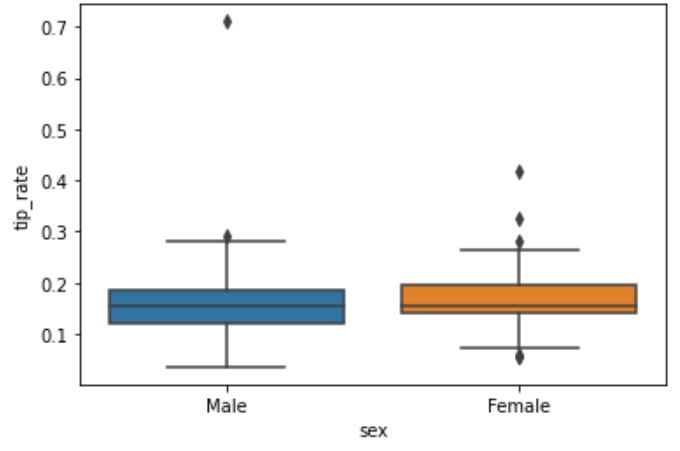
# 箱ひげ図
# plt.boxplot(df['tip_rate'])
# plt.show()
sns.boxplot(x='sex', y='tip_rate', data=df)

stats_sns.boxplot().jpg

・平均偏差(MD：mean deviation)

平均(もしくは中央値)からの偏差の絶対値の平均。
全てのデータを扱うので、散布度としては適している。
次の数式で表される

  • $MD=\frac{1}{n}(|x_1-\bar{x}|+…+|x_n-\bar{x}|)=\frac{1}{n}\sum_{i=1}^n|x_i-\bar{x}|$

絶対値は扱いにくいので2乗する。⇒ 分散

・分散(variance)

平均からの偏差の2乗の平均
通常は標本の分散は$s^2$、母集団の分散は$σ^2$と表す。
nではなくn-1で割る不偏分散もよく使用される(後述)
次の数式で表される。

  • $s^2=\frac{1}{n}((x_1-\bar{x})^2+…+(x_n-\bar{x})^2)=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2$

2乗すると尺度がずれる(扱う値がデータに対して大きくなりすぎる)ので平方根を取る。⇒ 標準偏差

・標準偏差(standard deviation)

分散の平方根。
通常は標本の分散はs、母集団の分散はσと表す。
次の数式で表される。

  • $σ=\sqrt{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2}$

散布度を表す際は、分散と標準偏差がよく使用される。
分散と標準偏差がわかれば、データの散布度がなんとなくわかる。
stats_mean_and_std.jpg
※左は平均±標準偏差、右はデータの何％がその範囲に含まれているか

分散はnp.var(data)、標準偏差はnp.std(data)で算出可能。

# 分散
np.var(df['tip'])  # -> 1.9066085124966428

# 標準偏差
np.std(df['tip'])  # -> 1.3807999538298958

■2変数間の記述統計

▶共分散(covariance)

2変数間の相関関係を表す指標。
(例：身長と体重、総額とチップ額など...)

変数1の分散：$s^2_x=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2$

変数2の分散：$s^2_y=\frac{1}{n}\sum_{i=1}^n(y_i-\bar{y})^2$

散布図(scatter plot)：$s_{xy}=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})$
stats_covariance.jpg

・共分散行列(covarianse matrix)

複数の変数間の共分散を行列で扱う方法。
変数が多くなると行列で扱うほうが便利(拡張性がある)になってくる。
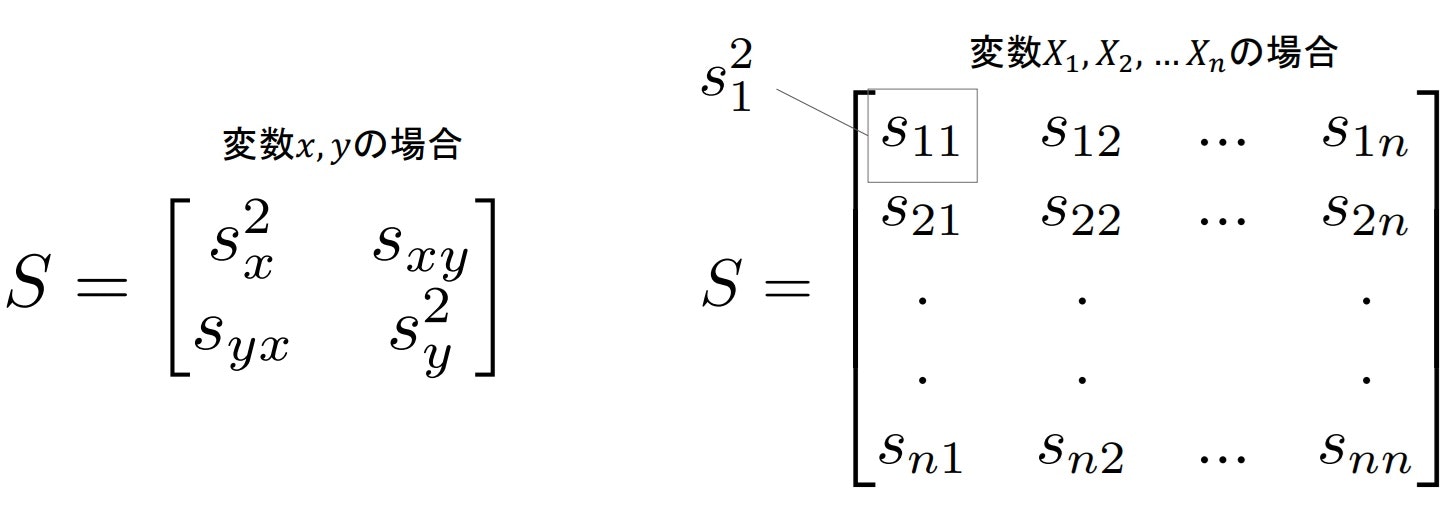
stats_covariance_matrix.jpg

共分散はnp.cov(xarray, yarray, bias=True)で算出可能(bias=Tureとすることで、n-1ではなく、nで割ってくれる)

共分散行列はnp.cov(nparray, bias=True)、df.cov()で算出可能(df.cov()は不偏分散となるので注意)

# 共分散
np.cov(df['total_bill'], df['tip'], bias=True)

array([[78.92813149, 8.28938892],
          [ 8.28938892, 1.90660851]])

# 共分散行列
# np.stack()でarrayを結合
x = np.stack([df['total_bill'], df['tip'], df['size']], axis=0)
np.cov(x, bias=True)

array([[78.92813149, 8.28938892, 5.04522121],
          [ 8.28938892, 1.90660851, 0.64126747],
          [ 5.04522121, 0.64126747, 0.9008835 ]])

# df.cov()は不偏共分散行列を返す(nではなくn-1で割った時の分散と共分散であることに注意)
df.cov()
total_bill tip size tip_rate
total_bill 79.252939 8.323502 5.065983 -0.184107
tip 8.323502 1.914455 0.643906 0.028931
size 5.065983 0.643906 0.904591 -0.008298
tip_rate -0.184107 0.028931 -0.008298 0.003730

▶相関係数(correlation coefficient)

共分散を標準化したので、相関係数。
共分散の取りうる値(最小値～最大値)を計算し、‐1～1の範囲に変換する。

  • $-S_xS_y\leqq S_{xy}\leqq S_xS_y$ ⇒ $-1\leqq \frac{S_{xy}}{S_xS_y}\leqq 1$ (相関係数：ピアソンの積率相関係数)
    ※左の式に$\frac{1}{S_xS_y}$をかけて、右のように標準化する。
    ※プロットが直線状にあればあるほど、$S_xS_y$の値は最大になる。

感覚的な相関の強さは下記のようになる。
stats_correlation_power.jpg

・正の相関、負の相関、無相関

stats_scatter_covariance.jpg

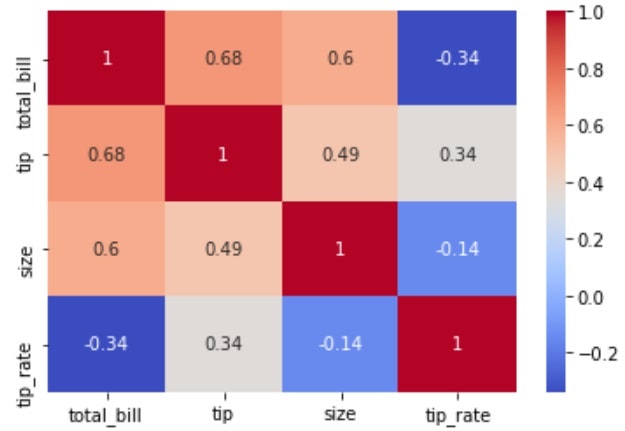
・相関行列(correlation matrix)

共分散と同様に相関係数にも行列表現が存在する。
対角要素は1となる。
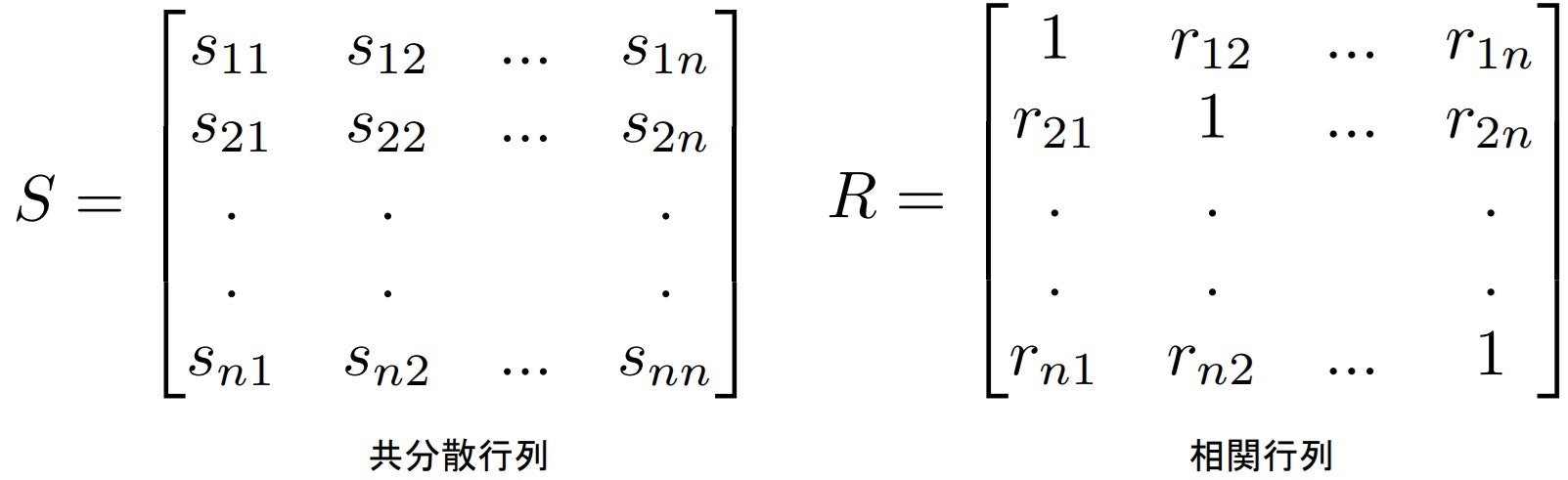
stats_correlation_matrix.jpg

np.corrcoef(xarray, yarray)やnp.corrcoef(nparray)、df.corr()で算出することが可能。
sns.heatmap(df.corr())でよく見る相関係数のヒートマップを描画可能。

# 相関行列
np.corrcoef(df['total_bill'], df['tip'])

x = np.stack([df['total_bill'], df['tip'], df['size']], axis=0)
np.corrcoef(x)

df.corr()
total_bill tip size tip_rate
total_bill 1.000000 0.675734 0.598315 -0.338624
tip 0.675734 1.000000 0.489299 0.342370
size 0.598315 0.489299 1.000000 -0.142860
tip_rate -0.338624 0.342370 -0.142860 1.000000 
# 相関行列をheatmapを使って表示
sns.heatmap(df.corr(), cmap='coolwarm', annot=True)

stats_heatmap(df.corr()).jpg

▶連関係数(association)

  • カテゴリ変数間の相関関係。
  • 分割表(contingency table)を用いて計算する。
  • 分割表内の数字(度数)で連関があると思われるものは観測度数(observed frequency)といい、連関がないと想定した場合の度数は期待度数(expected frequencies)といわれる。

例：お酒を飲む人ほどタバコを吸う傾向にあるか？
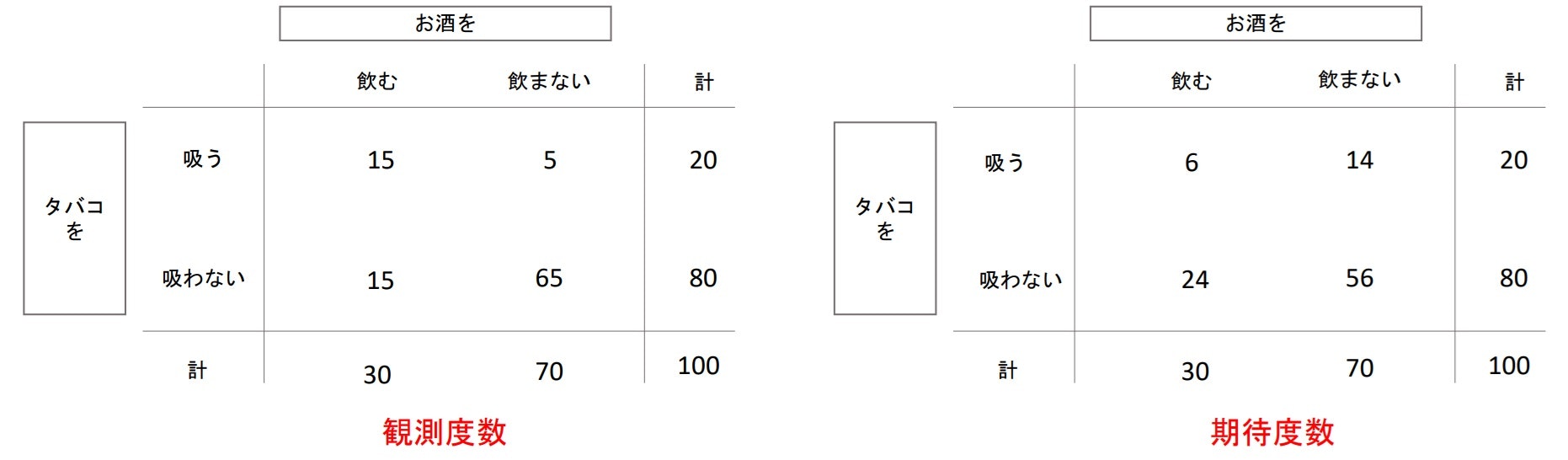
stats_contingency_table_two_version.jpg
右の表は「計」項目の割合とそれぞれのカテゴリの割合が同じなので、連関が無いといえるので期待度数となる。

▶カイ二乗(chi squared)

  • 観測度数から期待度数がどれほど離れているかを計算した値で、大きいほど連関があるということになる。
  • {$(観測度数-期待度数)^2$$/期待度数$}の総和

下記の式で表せる。
$χ^2=\sum_{i=1}^a\sum_{j=1}^b\frac{(n_{ij}-e_{ij})^2}{e_{ij}}$
※a行b列の分割表におけるi行j列で、$n_{ij}$：観測度数、$e_{ij}$：期待度数
stats_chi_squared.jpg
これも2乗のままだと使いにくいので標準化する。 -> クラメールの連関係数

pd.crosstab(xarray, yarray)で分割表のDataFrameを出力可能で、xarrayがindex、yarrayがcolumnになる。

stats.chi2_contingency(cont_table, correction=False)でカイ二乗値と期待度数を算出することができる。(第一戻り値がカイ二乗値、第4戻り値が期待度数)
cont_tableは分割表を指定する。

# 分割表
cont_table = pd.crosstab(df['sex'], df['time'])

# 第一戻り値がカイ二乗, 第四戻り値が期待度数
a, _, _, b = stats.chi2_contingency(cont_table, correction=False)
a  # -> 10.277251918677742
b  # -> array([[ 43.75409836, 113.24590164],
   #           [ 24.24590164,  62.75409836]])

▶クラメールの連関係数

  • $χ^2$値を0～1に標準化した値

次の式で表せる。
$V=\sqrt{\frac{χ^2}{(min(a,b)-1)N}}$(N：標本数)
※分割表の行数aと列数bの小さいほうの値が「min(a,b)」の値となる。
-> 今回であれば、行数2、列数2なのでmin(a,b)は2になる

pythonにクラメールの連関係数を求める関数は実装されていないので、自分で定義する必要がある。

# クラメールの連関係数
def cramers_v(x, y):
    cont_table = pd.crosstab(x, y)
    chi2 = stats.chi2_contingency(cont_table, correction=False)[0]
    min_d = min(cont_table.shape) - 1
    n = len(x)
    return np.sqrt(chi2/(min_d*n))

次の記事

Python初心者の備忘録 #12 ~統計学入門編02~

0
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
3