一般的に利用される損失関数をtensorflowにて実装しました。
回帰
L2ノルム(ユークリッド損失関数)
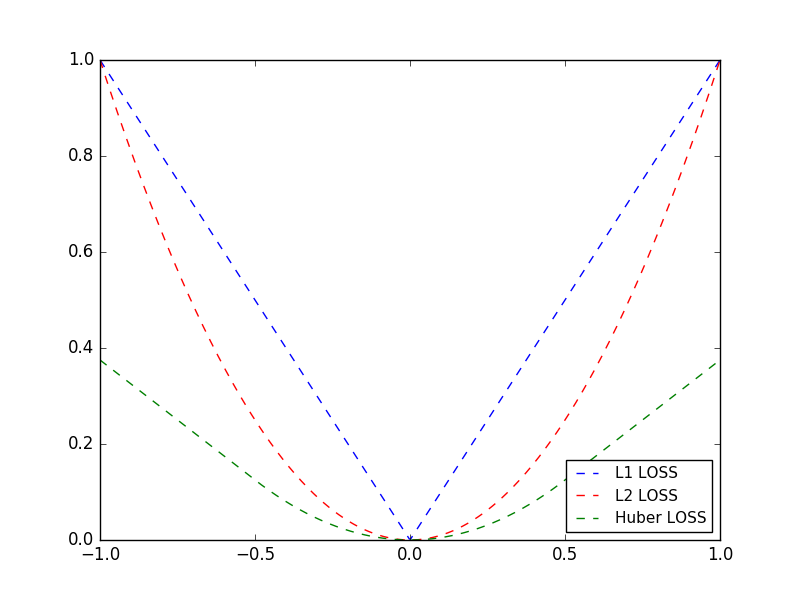
L2ノルムの損失関数は目的値への距離の二乗で表されます。
L2ノルム損失関数は、目的値の近くでとがった急なカーブを描いていることが特徴です。
つまりアルゴリズムは目的値にゆっくり近づきながら収束することができます。
L2 = (target-predict)^2
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1., 1., 500)
y = np.zeros(500)
target = tf.placeholder(tf.float32, [500])
predict = tf.placeholder(tf.float32, [500])
l2_loss = tf.square(target-predict)
with tf.Session() as sess:
l2_output = sess.run(l2_loss, feed_dict={target: y, predict: x})
plt.plot(x, l2_output, 'b--', label='L2 LOSS')
plt.show()
L1ノルム(絶対値損失関数)
L1ノルム損失関数は、距離の絶対値で表されます。
値が大きくなっても勾配が急にならないため、L1ノルムはL2ノルムよりも外れ値にうまく対応することができます。
しかし、目的値に対して滑らかではないため、うまく収束しない可能性があります。
L1 = |target-predict|
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1., 1., 500)
y = np.zeros(500)
target = tf.placeholder(tf.float32, [500])
predict = tf.placeholder(tf.float32, [500])
l1_loss = tf.abs(target-predict)
with tf.Session() as sess:
l1_output = sess.run(l1_loss, feed_dict={target: y, predict: x})
plt.plot(x, l1_output, 'b--', label='L1 LOSS')
plt.show()
Hurber損失関数
hurber損失では、ズレがある範囲内ならば二乗損失を、それより外なら直線上に増加する損失を与えます。
一定範囲内に対しては厳しく損失を与え、逆に外の方では損失の増加が直線的になります。
学習データに仮に外れ値があった場合に、それらに引っ張られる学習が抑えられます。
L_\delta(a) = \begin{cases}
\frac{1}{2}a^2 & for\ |a|<\delta \\
\delta(|a|-\frac{1}{2}\delta) & (otherwise)
\end{cases}
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1., 1., 500)
y = np.zeros(500)
def huber_loss(prediction, label, delta=0.5):
error = label - prediction
cond = tf.abs(error) < delta
squared_loss = 0.5 * tf.square(error)
linear_loss = delta * ( tf.abs(error) - 0.5 * delta)
return tf.where(cond, squared_loss, linear_loss)
with tf.Session() as sess:
huber_output = sess.run(huber_loss(x, y))
plt.plot(x, huber_output, 'g--', label='Huber LOSS')
plt.show()
分類
ヒンジ損失関数
SVMにてよく使われる損失関数です。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3., 5., 500)
y = np.ones(500)
target = tf.placeholder(tf.float32, [500])
predict = tf.placeholder(tf.float32, [500])
hinge_loss = tf.maximum(0., 1 - tf.multiply(target, predict))
with tf.Session() as sess:
hinge_output = sess.run(hinge_loss, feed_dict={target: y, predict: x})
plt.plot(x, hinge_output, 'b--', label='HINGE LOSS')
plt.show()
ロジスティック損失関数
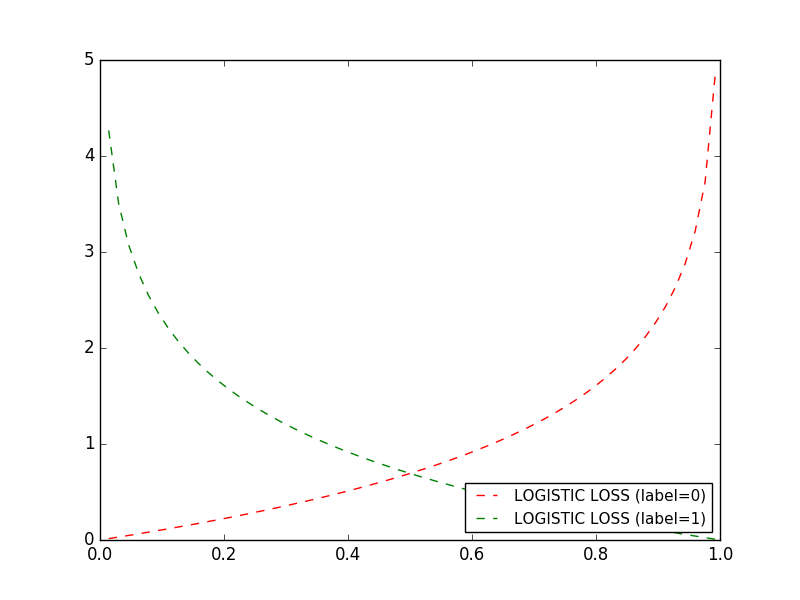
ロジステック回帰はインスタンスが特定のクラスに属する確率を推定するためによく利用します。
推定された確率が50%以上なら、モデルはインスタンスがそのクラスに属する(label=1)と予測します。
そうでなければ、インスタンスはそのクラスに属さない(label=0)と予測します。
ロジスティック回帰モデルは
\hat{p}=h_\theta(x) = \sigma(\theta^T \cdot x)
にて表され、$\sigma(t)$はシグモイド関数です。
\sigma = \frac{1}{1 + exp(-t)}
ロジスティック回帰モデルによってインスタンスが陽性クラス(label=1)に属する確率$\hat{p}=h_\theta(x)$が推定されたら予測$\hat{y}$は以下のように得られます。
\bar{y} = \begin{cases}
0 & if\ \hat{p}<0.5 \\
1 & if\ \hat{p}>0.5
\end{cases}
訓練の目的は、モデルが陽性インスタンスに対して高い確率、陰性インスタンスには低い確率を推定できるようにするにパラメータ$\theta$を設定することです。ロジスティック損失関数は以下のようになります。
J(\theta)=-y^{(i)}log(\hat{p}^{(i)})-(1-y^{(i)})log(1-\hat{p}^{(i)})
モデルが陽性インスタンス(label=1)に対して0に近い確率を推定するとコストが大きくなり、陰性インスタンス(label=0)に対して1に近い確率を推定するとコストが大きくなることがわかります。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3., 5., 500)
y = np.ones(500)
y_ = np.zeros(500)
target = tf.placeholder(tf.float32, [500])
predict = tf.placeholder(tf.float32, [500])
entropy_loss = -tf.multiply(target, tf.log(predict)) - \
tf.multiply((1. - target), tf.log(1. - predict))
with tf.Session() as sess:
entropy_output = sess.run(entropy_loss, feed_dict={target:y, predict:x})
entropy_output_ = sess.run(entropy_loss, feed_dict={target:y_, predict:x})
plt.plot(x, entropy_output_, 'r--', label='LOGISTIC LOSS (label=0)')
plt.plot(x, entropy_output, 'g--', label='LOGISTIC LOSS (label=1)')
plt.legend(loc='lower right', prop={'size': 11})
plt.show()
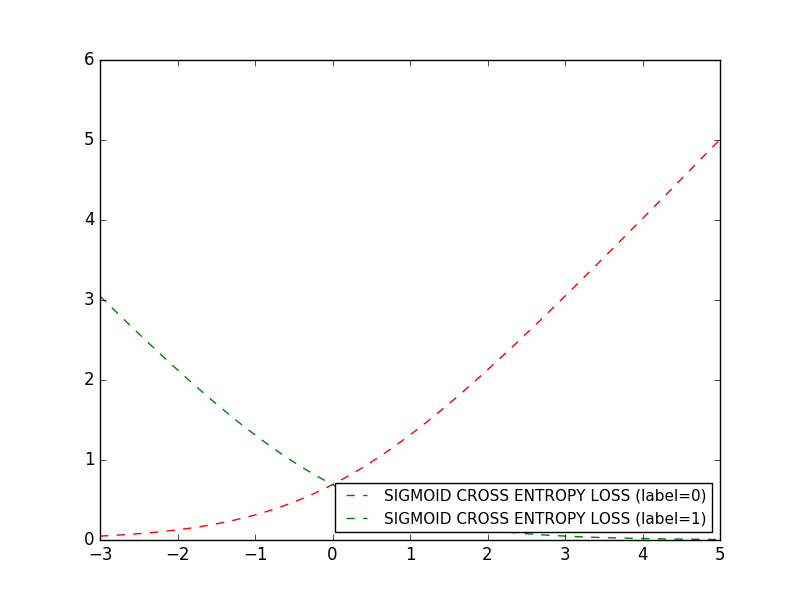
シグモイド交差エントロピ損失関数
シグモイド関数はロジスティック損失関数と似ていますが、入力データをシグモイド関数で変換してからロジスティック損失関数に渡す違いがあります。
詳細はtensorflowのホームページを参考にしてみて下さい。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3., 5., 500)
y = np.ones(500)
y_ = np.zeros(500)
predict = tf.placeholder(tf.float32, [500])
target = tf.placeholder(tf.float32, [500])
sigmoid_cross_entropy_loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=predict, labels=target)
with tf.Session() as sess:
loss = sess.run(sigmoid_cross_entropy_loss, feed_dict={predict: x, target: y})
loss_ = sess.run(sigmoid_cross_entropy_loss, feed_dict={predict: x, target: y_})
plt.plot(x, loss_, 'r--', label="SIGMOID CROSS ENTROPY LOSS (label=0)")
plt.plot(x, loss, 'g--', label="SIGMOID CROSS ENTROPY LOSS (label=1)")
plt.legend(loc='lower right', prop={'size': 11})
plt.show()
https://www.tensorflow.org/api_docs/python/tf/nn/sigmoid_cross_entropy_with_logits
ソフトマックス交差エントロピー損失関数
ソフトマックス回帰モデル
ソフトマックス回帰モデルは、インスタンス$x$を受け取ると、まず個々のクラスkのスコア$s_k(x)$を計算し、ソフトマックス関数を適用して個々のクラスの確率を推定します。
ソフトマックス関数は、すべてのスコアの指数を計算してから、結果を正規化しています。
softmax(x_i)=\frac{exp(s_i)}{\sum_{k=1}^{K}exp(s_k)}
交差エントロピー(cross entropy)
訓練の目的は、ターゲットクラスを高い確率で推定するモデルをつくることです。
2つの確率分布P, Qに対して
cross\ entropy=-\sum_xP(x)logQ(x)
を交差エントロピーと言います。
PとQが二値変数の場合、
\begin{cases}
P(x_1) = p,\ P(x_2)=1-p \\
Q(x_1) = q,\ Q(x_2)=1-q
\end{cases}
ロジスティック損失関数と等しくなることがわかります。
cross\ entropy = -p\cdot log(q)-(1-p)\cdot log(1-q)
tensorflowにてsoftmax交差エントロピー損失関数を実装する方法は
- マニュアルで計算グラフを構築
- softmax_cross_entropy_with_logitsを利用
- sparse_softmax_cross_entropy_with_logitsを利用
があります。
import tensorflow as tf
import numpy as np
logits = tf.placeholder(tf.float32, [None, 3])
labels = tf.placeholder(tf.float32, [None, 3])
sparse_labels = tf.placeholder(tf.int32, [None])
## manual
softmax = tf.nn.softmax(logits)
loss_0 = -tf.reduce_sum(tf.log(softmax) * labels, axis=1)
## softmax_cross_entropy_with_logits
loss_1 = tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits)
## sparse_softmax_cross_entropy_with_logits
loss_2 = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=sparse_labels, logits=logits)
x = np.array([[6,5,4],
[2,5,4],
[3,1,6]])
y = np.array([[1,0,0],
[0,1,0],
[0,0,1]])
sparse_y = np.array([0,
1,
2])
with tf.Session() as sess:
loss = sess.run([loss_0, loss_1, loss_2],
feed_dict={logits:x, labels:y, sparse_labels:sparse_y})
for i in range(len(loss[0])):
print('target1: %.8f, target2: %.8f, target3: %.8f'
% (loss[0][i], loss[1][i], loss[2][i]))