LoginSignup
2
7

More than 3 years have passed since last update.

@YuSAS

ニューラルネットワークの初歩について学習

Last updated at Posted at 2021-08-01

今回の記事では、ニューラルネットワークについて、Udemyの講座にて学習した内容を要約する。なお、本記事に掲載しているコードは、すべて下記URLに掲載しているUdemy講座から抜粋している

Udemy講座URL
みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習 【2021年最新版】

目次

1.ニューラルネットワークの概要
2.単純ニューロンの実装
3.外部データの導入
4.ニューラルネットワークの実装

1-ニューラルネットワークの概要

  • ニューロン(神経細胞)を模したネットワーク
  • (人工)ニューロン：複数の入力データをニューロンで変換し、出力する
    • 各入力データとそれぞれの重みで積和演算を行う
    • 求めた値に対して更にバイアス値を追加する
    • 合計値を活性化関数で変換する
  • ニューラルネットワーク：複数の単純ニューロンの組み合わせ

2-単純ニューロンの実装

  • 入力：[1.0, 2.0 ,3.0]のリストを用意する
  • 重み：[1.5, 0.75, -1.0]
  • バイアス : 1.0
  • 活性化関数 : シグモイド関数を使用
    • 出力データを0～1の範囲に変換する
    • シグモイド関数については前回の記事にて記載
    • シグモイド関数は2値分類を行う際に使用される
      • 多値分類を行う際はソフトマックス関数が使用されることが多い
    • 各クラスのinitメソッド
      • インスタンスを生成する際に自動で実行される。
      • neural_network = NeuralNetwork()　の行の実行時にインスタンスを生成する
#ニューロン
class Neuron:
  def __init__(self):     # 初期設定
    self.input_sum = 0.0  # 入力データ合計値格納用変数
    self.output = 0.0     # 出力用変数

  def set_input(self, inp): # 入力データを足し合わせる
    self.input_sum += inp
    print("Input_sum : " + str(self.input_sum)) # デバッグ用

  def get_output(self):
    self.output = sigmoid(self.input_sum) #入力データの合計値を活性化関数を用いて変換
    return self.output

# ニューラルネットワーク
class NeuralNetwork:
  def __init__(self): # 初期設定
    self.neuron = Neuron() # ニューロンのインスタンス
    self.w = [1.5, 0.75, -1.0] # 重み
    self.bias = 1.0 # バイアス

  def commit(self, input_data): # 実行
    self.neuron.set_input(input_data[0] * self.w[0])
    self.neuron.set_input(input_data[1] * self.w[1])
    self.neuron.set_input(input_data[2] * self.w[2])
    self.neuron.set_input(self.bias)
    return self.neuron.get_output()

# ニューラルネットワークのインスタンス
neural_network = NeuralNetwork()

# 実行
input_data = [1.0, 2.0 ,3.0]
print("Output    : " + str(neural_network.commit(input_data)))
  • 出力結果は下記の通り
Input_sum : 1.5
Input_sum : 3.0
Input_sum : 0.0
Input_sum : 1.0
Output    : 0.7310585786300049

3-外部データの導入

3.1 外部データの確認

  • 今回は Iris dataset を導入する
    • 3品種、各50個の花のデータで構成
      • 0: Setosa
      • 1: Versicolor
      • 2: Versinica
    • 4つの測定値
      • Sepal length(cm)
      • Sepal width(cm)
      • Petal length(cm)
      • Petal width(cm)
    • scikit-learn ライブラリから Iris dataset を導入
    • 以下のコードで Iris dataset の中身を確認
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# Irisデータの読み込み
iris = datasets.load_iris()

# 各花のサイズ
iris_data = iris.data
print(iris_data.shape) # 形状
print(iris_data)
  • 実行結果から、50 × 3品種 のデータを確認できる
(150, 4)
[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 *****省略********
 [6.3 2.5 5.  1.9]
 [6.5 3.  5.2 2. ]
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]]
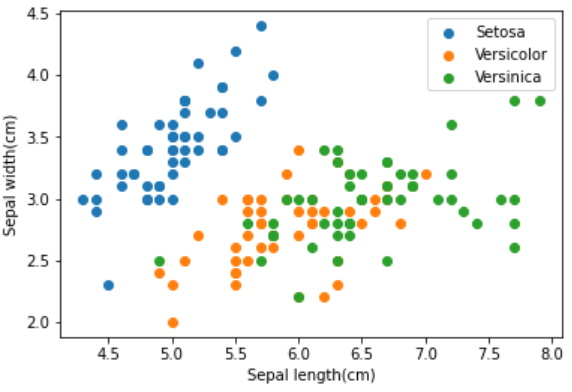
  • 散布図でSepal のデータを確認する
# Setosa
st_data = iris_data[:50]
# Versicolor
vc_data = iris_data[50:100]
# Versinica
vn_data = iris_data[100:150]

# Setosa      Sepal length(cm)・Sepal width(cm)
plt.scatter(st_data[:,0],st_data[:,1],label="Setosa")
# Versicolor  Sepal length(cm)・Sepal width(cm)
plt.scatter(vc_data[:,0],vc_data[:,1],label="Versicolor")
# Versinica   Sepal length(cm)・Sepal width(cm)
plt.scatter(vn_data[:,0],vn_data[:,1],label="Versinica")
plt.legend()

plt.xlabel("Sepal length(cm)")
plt.ylabel("Sepal width(cm)")
plt.show()
  • 出力された散布図から、Setosaとその他2品種には明確な境界線が確認できる

Iris_datasets散布図(Sepal).png

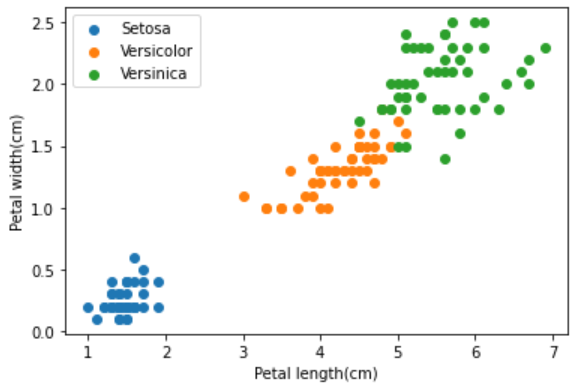
  • 同様にPetal のデータを散布図で確認する

Iris_datasets散布図(Pepal).png

3.2 単一ニューロンの実装

  • 今回はSetosaとVersicolorをSepal length/width のデータを用いて分類する
    • SetosaとVersicolor の2種類の分類を行う理由は、活性化関数としてシグモイド関数を用いているため
  • 以下のコードで入力データを作成している
    • 入力データの平均値を0に設定する
      • ニューラルネットワークの入力が偏ると、学習が進まない、あるいは学習に時間がかかるリスクがある
      • 偏りをなくすために平均値を0にする。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
iris_data = iris.data
sl_data = iris_data[:100, 0] # SetosaとVersicolor、Sepal length
sw_data = iris_data[:100, 1] # SetosaとVersicolor、Sepal width

# 平均値を0に
sl_ave = np.average(sl_data)  # Sepal length 平均値
sl_data -= sl_ave             # Sepal length 平均値を引く
sw_ave = np.average(sw_data)  # Sepal width  平均値
sw_data -= sw_ave             # Sepal width  平均値を引く

# 入力をリストに格納
input_data = []
for i in range(100):
    input_data.append([sl_data[i], sw_data[i]])
  • 単一ニューロン実装は以前の章にて説明済
  • 入力データが Sepal length と Sepal width の2次元のため、以下の変更が必要
    • ニューラルネットワーククラスの初期設定時の重み
    • ニューラルネットワーククラスのcommitのset_inputの回数
  • 入力データが Setosa と Versicolor で合計100個あるため、入力データ・出力データそれぞれリセットする機能が必要
    • リセット機能を追加しなければ前回の結果が残ったまま足し合わせてしまう。
    • リセットをコメントアウトすると総和が極端な値になり、いつも同じ分類結果になってしまう。
# ニューラルネットワーク
class NeuralNetwork:
    def __init__(self):         # 初期設定
        self.neuron = Neuron()  # ニューロンのインスタンス
        self.w = [0.5, -0.2]    # 重み
        self.bias = 0.0         # バイアス

    def commit(self, input_data):  # 実行
        self.neuron.reset() # input_sum と output をリセット

        self.neuron.set_input(input_data[0] * self.w[0]) # Sepal length
        self.neuron.set_input(input_data[1] * self.w[1]) # Sepal width
        self.neuron.set_input(self.bias)
        return self.neuron.get_output()
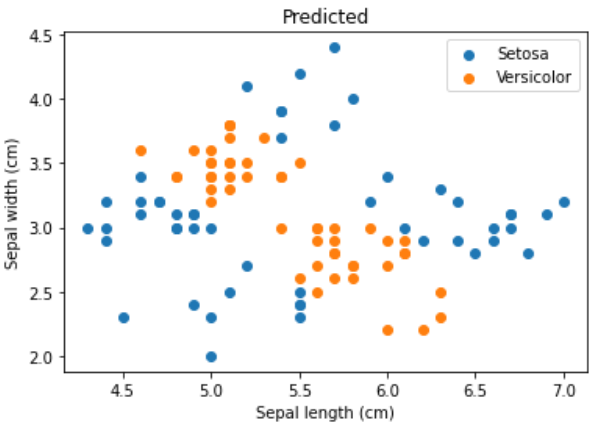
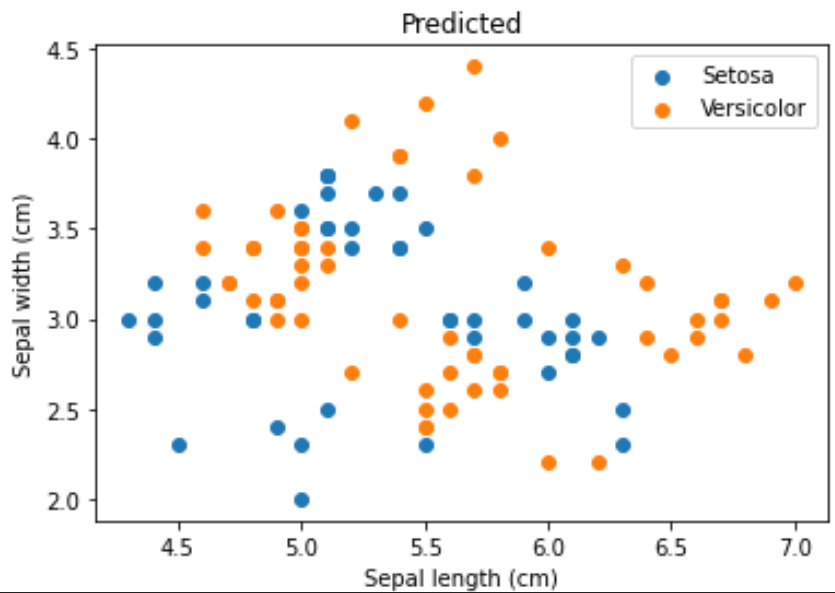
  • 出力結果が0.5を閾値として、SetosaとVersicolorを予測する
    • シグモイド関数の出力の範囲は0~1であり、中央値である0.5を閾値として設定する
    • 0.5を閾値とすることにより50%ずつ等確率の2クラス分類ができる
# 実行
st_predicted = [[], []]  # Setosa     x軸:length y軸:width
vc_predicted = [[], []]  # Versicolor x軸:length y軸:width
for data in input_data:
    predict_result = neural_network.commit(data)
    print("Output    : " + str(predict_result)) # デバッグ用
    if predict_result < 0.5:
        st_predicted[0].append(data[0]+sl_ave)
        st_predicted[1].append(data[1]+sw_ave)
    else:
        vc_predicted[0].append(data[0]+sl_ave)
        vc_predicted[1].append(data[1]+sw_ave)
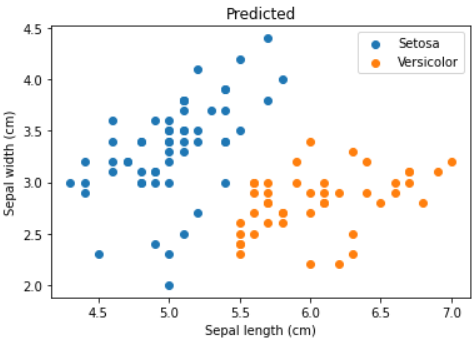
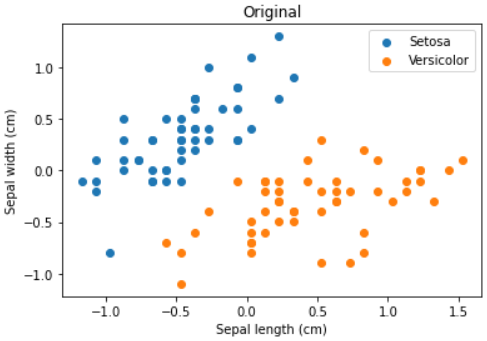
  • 散布図で予測結果(predict)を元のデータ(Original)と比較する

Iris_datasets散布図(predict).png

Iris_datasets散布図(original).png

4-ニューラルネットワークの実装

  • 前章で使用した Iris dataset を用いてニューラルネットワークを実装する
    • 入力層:2
    • 中間層:2
    • 出力層:1
    • ニューラルネットワーククラスの変更が必要
# ニューラルネットワーク
class NeuralNetwork:
    def __init__(self):                           # 初期設定
        self.w_im = [[4.0, 4.0], [4.0, 4.0]]      # 入力層-中間層  入力:2、ニューロン:2
        self.w_mo = [[1.0, -1.0]]                 # 中間層-出力層  入力:2、ニューロン:1

        # バイアス
        self.b_m = [2.0,-2.0]                     # 入力層-中間層  ニューロン数:2
        self.b_o = [-0.5]                         # 中間層-出力層  ニューロン数:1

        # 各層の宣言
        self.input_layer  = [0.0, 0.0]            # 入力層
        self.middle_layer = [Neuron(), Neuron()]  # 中間層
        self.output_layer = [Neuron()]            # 出力層

    def commit(self, input_data):  # 実行
       # 各層のリセット
       self.input_layer[0] = input_data[0]        # 入力層は値を受け取るのみ
       self.input_layer[1] = input_data[1]
       self.middle_layer[0].reset()
       self.middle_layer[1].reset()
       self.output_layer[0].reset()

       # 入力層(2)→中間層(2)
       self.middle_layer[0].set_input(self.input_layer[0] * self.w_im[0][0])  # Sepal length
       self.middle_layer[0].set_input(self.input_layer[1] * self.w_im[0][1])  # Sepal width
       self.middle_layer[0].set_input(self.b_m[0])

       self.middle_layer[1].set_input(self.input_layer[0] * self.w_im[1][0])  # Sepal length
       self.middle_layer[1].set_input(self.input_layer[1] * self.w_im[1][1])  # Sepal width
       self.middle_layer[1].set_input(self.b_m[1])

       #中間層(2)→出力層(1)
       self.output_layer[0].set_input(self.middle_layer[0].get_output() * self.w_mo[0][0])
       self.output_layer[0].set_input(self.middle_layer[1].get_output() * self.w_mo[0][1])
       self.output_layer[0].set_input(self.b_o[0])

       return self.output_layer[0].get_output()

Iris_datasets散布図(ニューラルネットワーク).png

  • また、中間層を3つに増やした場合、表現力が上がっていることが確認できる
    • ただしOriginalと比較して予測精度が上がったとは言えない
    • その場合、重みやバイアスを見直す必要がある

Iris_datasets散布図(ニューラルネットワーク-中間層3).png

参考文献

みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習 【2021年最新版】

2
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
7