今回の記事では、ニューラルネットワークの活性化関数として使用されているシグモイド関数について、Udemyの講座にて学習した内容を要約する。なお、本記事に掲載しているコードは、すべて下記URLに掲載しているUdemy講座から抜粋している
Udemy講座URL
みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習 【2021年最新版】
目次
1-関数の描画
- numpyをインポート
- 数学の計算ライブラリが多く入っている
- 大量データの取り扱いに向いている
import numpy as np
-
linspace
- 値が並んだ配列を作成
- 範囲を指定し、その区間を標準で50に区切る
- 区切る数を変更する場合はもう一つ引数を追加する
- 主にx軸などの範囲を決めるときに使用する
-
また、グラフを表示する際は matplotlib をインポートする
import matplotlib.pyplot as plt
- ここで下記関数を定義するコードの例を示す(抜粋)
$$y=2x+1$$
$$y=x^2-4$$
$$y=0.5x^3-6x$$
import numpy as np
x = np.linspace(-4, 4) # x軸の範囲は-4~4とする
y_1 = 2*x + 1 # 1次関数
y_2 = x**2 - 4 # 2次関数
y_3 = 0.5 * x**3 - 6*x # 3次関数
2-べき乗とネイピア数
- ネイピア数eの数値は下記の通り
$$e = 2.718281828459045...$$
- numpyをインポートしていると、np.eでネイピア数を利用することができる
import numpy as np
print(np.e)
- ネイピア数のべき乗の性質
- yの微小な変化/xの微小な変化(曲線の傾き)が元の関数に近づく
- 式の変形がしやすいため人工知能分野でよく使われる
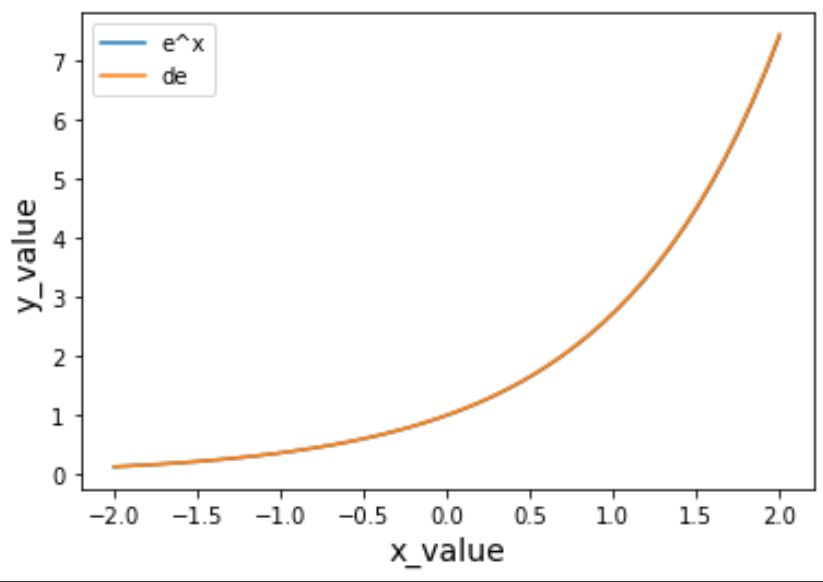
- 下記コードを実行することにより、曲線の傾きが元の関数に近づくことが確認できる
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 2)
dx = 0.01 #微小な変化
e = np.e #ネイピア数
y_e = e**x
y_de = (e**(x+dx) - e**x) / dx
plt.plot(x, y_e, label="e^x")
plt.plot(x, y_de, label="de")
plt.xlabel("x_value",size=14)
plt.ylabel("y_value",size=14)
plt.legend()
plt.show()
- 以下の式におけるnの値を大きくするとネイピア数の値に近づくことができる
$$(1+\frac{1}{n})^n$$
def approach_napier(n):
return (1 + 1/n)**n
3-シグモイド関数
- シグモイド関数は下記の通りの式で表現され、入力(x)から0~1の範囲に変換する
$$ y = \frac{1}{1+e^{-x}}$$
- シグモイド関数の傾きを求めるすなわち微分すると、下記の通りもとのシグモイド関数に置き換えて表現できるためよく使われる
$$ y{'} = y(1-y)$$
import numpy as np
import matplotlib.pyplot as plt
e = np.e #ネイピア数
# シグモイド関数
def sigmoid(x):
y = 1 / (1 + e**-x)
return y
# シグモイド関数を微分
def df_sigmoid(x):
d = sigmoid(x) * (1 - sigmoid(x))
return d
# 微小な変化
dx = 0.1
x = np.linspace(-8, 8)
y_sig = sigmoid(x)
# シグモイド関数の傾き
y_d = (sigmoid(x+dx) - sigmoid(x)) / dx
y_df = df_sigmoid(x)
plt.plot(x, y_sig ,label = "sigmoid")
plt.plot(x, y_d, label = "d_sigmoid")
plt.plot(x, y_df, label = "df_sigmoid")
plt.legend()
plt.xlabel("x",size=14)
plt.ylabel("y",size=14)
plt.grid()
plt.show()