この記事はバイオインフォマティクス Advent Calendar 2020の1日目の記事です
はじめに
僕はここ数年、テンソル(以下張量)分解を用いた教師無し学習による変数選択という手法を提案して実行し、去年はそれについて教科書も書きました。しかし、いかんせん張量分解は線形手法なので「所詮は線形でしょ?」みたいな扱いになってしまってイマイチアピーリングじゃありませんでした。カーネル化できればもうちょっと人口に膾炙するのでは、と思いながらなかなかアイディアがなく、内心、忸怩たる思いがありました。最近、割と簡単な方法でうまく行きそうなことがわかって原著論文も書きました。そこでここで宣伝することにします。
基本的なアイディア
アイディアは割とシンプルです。そんなんでいいならいちいち名前つけるなよ、という感じではあるんですが。例をカーネル主成分分析にとります。そのためにはまず、僕が張量分解を用いた教師無し学習による変数選択を提案する前にやっていた、主成分分析を用いた教師無し学習による変数選択を説明しないといけないです。$x_{ij} \in \mathbb{R}^{N \times M}$を$i$番目の遺伝子の$j$番目のサンプルにおける発現量としましょう。ここで$\sum_i x_{ij}=0, \sum_i x_{ij}^2=N$rとなるように規格化されているとします。主成分分析を用いた教師無し学習による変数選択ではグラム行列$x_{ii'} = \sum_j x_{ij}x_{i'j} \in \mathbb{R}^{N \times N}$を対角化して
$$
\sum_{i'} x_{ii'}u_{\ell i'} = \lambda_\ell u_{\ell i}
$$
となる固有ベクトル$u_{\ell i}$と固有値$\lambda_\ell$を求めます。これがいわゆる主成分得点と呼ばれるものです。これからサンプルに付加される主成分負荷量$v_{\ell j}$を
$$
v_{\ell j} = \sum_i x_{ij} u_{\ell i}
$$
で求めます。ちなみに$v_{\ell j}$は行列$x_{jj'} = \sum_i x_{ij}x_{ij'} \in \mathbb{R}^{M \times M}$の固有ベクトルです。なぜなら
$$
\sum_{j'} x_{jj'} v_{\ell j'} = \sum_{j'} \sum_i x_{ij}x_{ij'} v_{\ell j'} = \sum_{j'} \sum_i \sum_{i'} x_{ij}x_{ij'} x_{i'j'} u_{\ell i'} = \sum_i \sum_{i'} x_{ij} x_{ii'} u_{\ell i'} = \sum_i x_{ij} \lambda_\ell u_{\ell i} = \lambda_\ell v_{\ell j}
$$
なので。ちなみに
$$
u_{\ell i} = \sum_j x_{ij} v_{\ell j}
$$
でもあります。なぜなら
$$
\sum_{i'} x_{ii'} u_{\ell i'} = \sum_{i'} \sum_{j} x_{ij}x_{i'j} u_{\ell i'} = \sum_{i'} \sum_{j} \sum_{j'} x_{ij}x_{i'j} x_{i'j'} v_{\ell j'} = \sum_{j} \sum_{j'} x_{ij} x_{jj'} v_{\ell j'} = \sum_j x_{ij} \lambda_\ell v_{\ell j} = \lambda_\ell u_{\ell i}
$$
だからです。
さて、これをカーネル化するには
$$
\sum_i x_{ij}x_{ij'} \rightarrow k(x_{ij},x_{ij'})
$$
と置き換えて$k(x_{ij},x_{ij'}) \in \mathbb{R}^M$を対角化すればいいです。ここで$k(x_{ij},x_{ij})$がカーネル関数で、非負正定値であればどんなものでもOKです。有名なところではガウスカーネル(radial base function kernelともいいます)
$$
k(x_{ij},x_{ij'}) = \exp \left ( - \alpha \sum_i \left( x_{ij} - x_{ij'}\right)^2\right)
$$
(ここで$\alpha>0$は実数)とか多項式カーネル
$$
k(x_{ij},x_{ij'}) = \left (1 + \sum_i x_{ij}x_{ij'} \right)^d
$$
(ここで$d>0$は整数)などが有名です。ちなみに
$$
k(x_{ij},x_{ij'}) =\sum_i x_{ij}x_{ij'}
$$
は線形カーネルとも呼ばれます。
カーネル張量分解
さて、これを張量に応用します。$x_{ijk} \in \mathbb{R}^{N \times M \times K}$が与えられた時、張量分解は
$$
x_{ijk} = \sum_{\ell_1=1}^N \sum_{\ell_2=1}^M \sum_{\ell_3=1}^K G(\ell_1 \ell_2 \ell_3) u_{\ell_1 i} u_{\ell_2 j} u_{\ell_3 k}
$$
で与えられるとします。ここで$G \in \mathbb{R}^{N \times M \times K}$はコア張量、$u_{\ell_1 i} \in \mathbb{R}^{N \times N}, u_{\ell_2 j} \in \mathbb{R}^{M \times M}, u_{\ell_3 k} \in \mathbb{R}^{K \times K}$は特異値行列で直交行列です。張量分解にはいろいろあるのですがこれはタッカー分解というものです。ここで$x_{jkj'k'} = \sum_i x_{ijk}x_{ij'k'} \in \mathbb{R}^{M \times K \times M\times K}$を考えます。すると
$$
x_{jkj'k'} = \sum_i \sum_{\ell_1=1}^N \sum_{\ell_2=1}^M \sum_{\ell_3=1}^K \sum_{\ell_1'=1}^N \sum_{\ell_2'=1}^M \sum_{\ell_3'=1}^K G(\ell_1 \ell_2 \ell_3) G(\ell_1' \ell_2' \ell_3') u_{\ell_1 i} u_{\ell_2 j} u_{\ell_3 k}
u_{\ell_1' i} u_{\ell_2' j'} u_{\ell_3' k'}
$$
とかけるので$\delta_{\ell_1 \ell_1'} = \sum_i u_{\ell_1 i} u_{\ell_1' i}$($\delta_{\ell_1 \ell_1'}$はクロネッカーのδ)を用いると
$$
x_{jkj'k'} = \sum_{\ell_1=1}^N \sum_{\ell_2=1}^M \sum_{\ell_3=1}^K \sum_{\ell_2'=1}^M \sum_{\ell_3'=1}^K G(\ell_1 \ell_2 \ell_3) G(\ell_1 \ell_2' \ell_3') u_{\ell_2 j} u_{\ell_3 k}
u_{\ell_2' j'} u_{\ell_3' k'}
$$
となるので$G(\ell_2,\ell_3,\ell_2',\ell_3') = \sum_{\ell_1=1}^N G(\ell_1 \ell_2 \ell_3) G(\ell_1 \ell_2' \ell_3')$とすれば
$$
x_{jkj'k'} = \sum_{\ell_2=1}^M \sum_{\ell_3=1}^K \sum_{\ell_2'=1}^M \sum_{\ell_3'=1}^K G(\ell_2,\ell_3,\ell_2',\ell_3')u_{\ell_2 j} u_{\ell_3 k}
u_{\ell_2' j'} u_{\ell_3' k'}
$$
となるので、$x_{jkj'k'}$を張量分解すれば$u_{\ell_2 j},u_{\ell_3 k}$を求めることができることが分かります。
ここまでくればあとは簡単です。主成分分析の時と同じように
$$
\sum_i x_{ijk}x_{ij'k'} \rightarrow k(x_{ijk},x_{ij'k'})
$$
としてから$k(x_{ijk},x_{ij'k'}) \in \mathbb{R}^{M \times K \times M \times K}$を張量分解すればカーネル化された張量分解を計算できます。ガウスカーネルなら
$$
k(x_{ijk},x_{ij'k'}) = \exp \left ( - \alpha \sum_i \left( x_{ijk} - x_{ij'k'}\right)^2\right)
$$
だし、多項式カーネルなら
$$
k(x_{ijk},x_{ij'k'}) = \left (1 + \sum_i x_{ijk}x_{ij'k'} \right)^d
$$
でいいわけです。
スイスロール
カーネル張量分解で非線形な関係が可視化できるかどうかスイスロール構造で試してみましょう。
N=1000
p = sqrt(2 + 2 * seq(-1, 1 - 2/N, 2/N))
set.seed(0)
d_sr <- array(NA,c(1000,3,10))
for (i in c(1:10))
{
y = 2 * runif(N, -1, 1)
d_sr[,,i] = cbind(p * cos(2*pi*p), y, p * sin(2*pi*p))
}
color <- vector()
for(i in 1:N){
color[i] = rainbow(ceiling(N/50))[ceiling(i/50)]
}
labels=seq(N)
d_sr<- apply(d_sr,2:3,scale)
pairs(d_sr[,,1],col=color,pch=16)
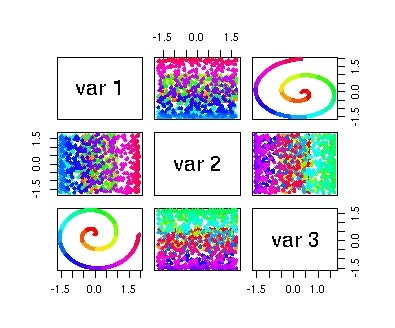
$x_{ijk} \in \mathbb{R}^{1000 \times 3 \times 10}$は3次元空間に埋め込まれた1000個の点からなるスイスロール構造を乱数を変えて10個束ねた張量になっています。このうちの一個をただ特異値分解すると、
SVD <- svd(d_sr[,,1])
colnames(SVD$u) <- c("l=1","l=2","l=3")
pairs(SVD$u[,1:3],col=color,pch=16)
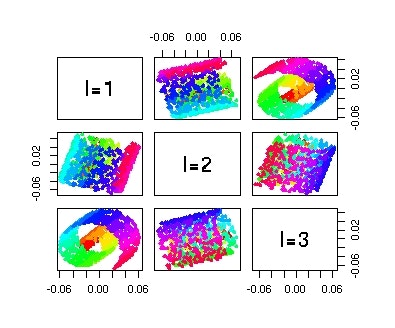
みたいになってしまいます。あたりまえですが、スイスロールの渦巻きに沿った座標を取り出すことには成功していません。
線形カーネルを用いたタッカー分解(ここではHOSVDと呼ばれるアルゴリズムを採用します)を適用すると
require(rTensor)
HOSVD <- hosvd(as.tensor(d_sr),c(10,3,10))
pairs(HOSVD$U[[1]][,1:3],col=color,pch=16,labels=c("l1=1","l1=2","l1=3"))
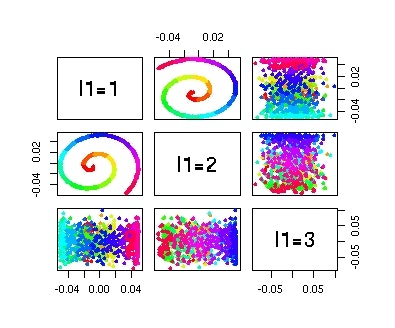
みたいな感じです。斜めから見る感じになってない分、特異値分解よりはましですが、スイスロールの渦巻きに沿った座標を取り出すことには成功していません。
次にガウスカーネル($\alpha=0.01$)を試してみましょう。
a <- d_sr
a <- aperm(a,c(2,1,3))
dim(a) <- c(3,10^4)
DD <- (abs(outer(colSums(a^2),colSums(a^2),"+") - 2 *t(a) %*% a))^0.5
dim(DD) <- c(1000,10,1000,10)
HOSVD <- hosvd(as.tensor(exp(-DD^2/10^2)),c(3,1,3,1))
pairs(HOSVD$U[[1]][,1:3],col=color,pch=16,labels=c("l1=1","l1=2","l1=3"))
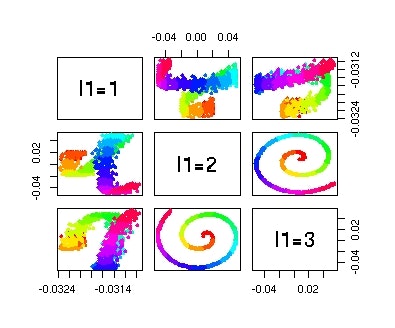
今度は不完全ながらスイスロールの渦巻きに沿った座標を取り出すことには成功しています。なのでこれでカーネル化した張量分解が可能だということが確認できました。
カーネル張量分解を用いた教師なし学習による変数選択
以下ではこれをいわゆるlarge p small n問題に適用します。張量分解を用いた教師なし学習による変数選択はもともと、遺伝子の数は数万個あるのに、サンプルは数個から数十個しか取れない極端なlarge p small n問題において変数選択を行うことが目的でした。数万個遺伝子があっても、例えば、患者と健常者に差がある遺伝子は数十個から数百個しか無いことが多く、数万個の遺伝子の数パーセント以下である。こういう場合に遺伝子を選ぶのは簡単ではなく、張量分解を用いた教師なし学習による変数選択はこのタスクをうまくやることができることが知られている(たとえばこれとこれ)。
ここでは原著論文の内容から抜粋してlarge p small n問題の時にカーネル張量分解を用いた教師なし学習による変数選択がどれくらいうまく行くものなのか見てみる。
人工データ
まずは以下の様な人工データ$x_{ijk} \in \mathbb{R}^{N \times M \times M}$を考える。
x_{ijk} \sim \left \lbrace \begin{array}{cc}
{\cal N}(\mu, \sigma) & i \le N_1 \le N , j,k \le \frac{M}{2} \\
{\cal N}(0, \sigma) &それ以外
\end{array}\right.
意味としては$N$個の変数のうち$N_1$子だけが$j,k \leq M/2$とそれ以外で差がある、という状況である。$j,k$は何らかの実験条件(例えば、男性vs女性とか若者vs老人とか日本人vsアメリカ人とか)を表現していて、$M$実験条件が$M/2$のところ2分されているみたいなことを想定してる。large p small n問題にするため$N \gg M$の状況を考える。${\cal N}(\mu,\sigma)$は平均が$\mu$で標準偏差が$\sigma$のガウス分布である。
使用したカーネルは
K(x_{ijk},x_{ij'k'}) = \sum_i x_{ijk}x_{ij'k'} \\
= \exp \left \lbrace - \alpha \sum_i \left ( x_{ijk} - x_{ij'k'} \right )^2\right \rbrace \\
= \left ( 1 + \sum_i x_{ijk}x_{ij'k'} \right)^d
(上から順に線形、ガウス、多項式)の3つである。カーネル張量分解(KTD)とカーネルPCA(KPCA)の両方を試した。カーネルPCAの場合は、張量を$x_{i(jk)} \in \mathbb{R}^{N \times M^2}$の様な行列としてPCAを計算した。パフォーマンスの評価は以下の様にした。カーネルPCAの場合には主成分負荷量$v_{\ell (jk)} \in \mathbb{R}^{M^2}$に対して、$j,k \leq M/2$の$M^2/4$個とそれ以外の$M^2 - M^2/4 = 3M^2/4$個の2群にt検定を適用し、各$\ell$について、$M^2$個のP値を計算した。カーネル張量分解については$M/2$を境にして2群の検定とし$u_{\ell_2 j}$、$u_{\ell_3 k}$のそれぞれについ$M$個ずつP値を計算した。最小の$P$値をパフォーマンスの評価とし、100回の乱数発生に対して幾何平均した。
上記は$N = 1000, N_1 = 10, M = 6, \mu = 2, \sigma = 1$の場合のパフォーマンスである。線形カーネルのKPCAはただのPCAと同じである。まず、気づくことは多項式カーネルは線形カーネルより悪い、ということである。多項式カーネルは線形+べき乗の基底空間で計算した場合と等価であることが知られているので多項式カーネルが線形カーネルより悪いということは空間を広げた結果、却って特徴をとらえた低次元空間を作りにくくなってしまったということを意味する。多項式カーネルでは基本的に2群に有意差がある主成分負荷量や特異値ベクトルを得ることができていない。それではガウスカーネル(RBF)と線形カーネルではどうかというと、多重比較補正しないP値ではカーネルPCAとカーネル張量分解で差がみられない。だが、多重比較補正すると差がでる。PCAの場合は$M^2$個のP値に対して多重比較補正しなくてはいけないのに対して、張量分解の場合は$2M$個のP値に対して多重比較補正をすればいいので$M=6$といった少数の場合でも、多重比較補正すると差が出てくる。
多重比較補正した後では線形カーネルとガウスカーネルには差がみられない。スイスロールの場合には明確に差があったのになぜだろうか?それは以下の様に考えられる。スイスロールの場合は点が1000個もあり、十分複雑な構造を表現できた。しかし、$M^2=36$個の点では複雑な構造を表現することができない。したがって、ガウスカーネルを導入しても線形カーネルの性能を越えられないのだと思われる。これだとカーネル張量分解を考えた意味がないようにも思えるが、逆に言えばlarge p small n問題の場合は線形カーネルの範囲ですでに非線形を考えてもベストの解が得られているということがわかる。これは多項式カーネルにしたら線形カーネルより悪くなってしまったことからも明らかである。いままでの研究で(線形の)張量分解を用いた教師なし学習による変数選択法はlarge p small n問題の場合は他のどんな方法より性能がよいことが経験的に知られていた。非線形の拡張しても線形を越えられないことから、すでにベストの解が得られているので他の方法では張量分解を用いた教師なし学習による変数選択法を越えられなかったのだと判る。
SARS-CoV-2 データセット
人工データでは差が出なかった線形カーネルとガウスカーネルを用いたカーネル張量分解だが、現実のデータではどうだろうか?ここでは我々の既報で張量分解を用いた教師なし学習による変数選択法がうまくいくことが分かっているSARS-CoV-2の感染データセットを考えよう(Qiitaでの説明記事はこちら)。このデータセットは$x_{ijkm} \in \mathbb{R}^{N \times 5 \times 2 \times 3}$の張量の形式でフォーマットできる。$N$は遺伝子数、5は使用した培養細胞の種類数、2は感染の有無、3はbiological replicateの数である。これから線形カーネルとガウスカーネルで$x_{jkmn'k'm'} = k(x_{ijkm},x_{ij'k'm'}) \in \mathbb{R}^{5 \times 2 \times 3 \times 5 \times 2 \times 3 }$を作り張量分解を行う。
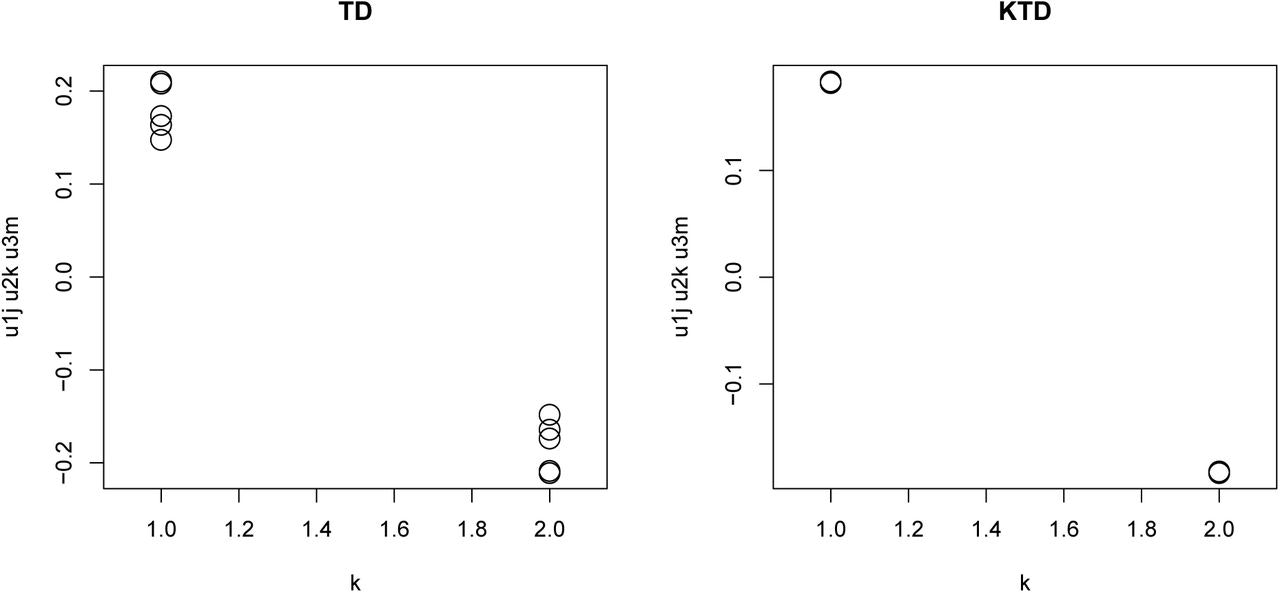
結果を見ると$u_{1 j}$と$u_{1 m}$が$j,m$依存性が無く、$\ell_2=2$の時に$u_{\ell_2 1} = -u_{\ell_2 2}$になっているので$u_{1j}u_{2k}u_{1m}$を計算すれば感染($k=1$)と非感染($k=2$)の差がもっともよく見えるはずである。上図はその結果だが、差が出なかった人工データの時とことなりカーネル張量分解の方が明らかに感染と非感染の差がはっきりでている。$k$を固定した場合、培養細胞5種類とbiological replicate3個で各15サンプルずつあるはずなのだが、カーネル張量分解の方は点が重なってしまってみえないくらい一致している。やはり、人工データよりも現実のデータの方が解析が難しく、カーネル張量分解にすることで線形カーネルを越える性能を出せることが分かる。
おわりに
数年前から「張量分解を用いた教師なし学習による変数選択法」を提案してきたが、線形の教師なし学習であるためコントロールできるパラメータが無く、うまく行かない場合、よりよい結果を得たい場合に、改善の方法が無かった。今回、カーネル張量分解を用いた教師なし学習による変数選択法に拡張することに成功した。人工データではlarge p small n問題の場合にガウスカーネルは線形カーネルを越えることができなかったが、現実のデータを用いた場合には結果を改善することに成功した。張量分解を用いた教師なし学習による変数選択法自体が非常に強力な方法で大抵の場合よい結果をだしてしまうため、カーネル張量分解を用いた教師なし学習による変数選択法が有効に活用される場合を探すのは難しいかもしれないが、今後、そのようなデータを探していきたい。
