この記事は創薬 (dry) Advent Calendar 2020の2日目の記事です。
IBIS2020で発表した時のスライドとビデオもあります。併せてご覧ください。
はじめに
テンソル分解を用いた教師無し学習による変数選択法を用いてCOVID-19治療薬候補化合物のリポジショニングを行った(論文)のでその内容を報告する。
テンソル分解を用いた教師無し学習による変数選択
基本的にこちらの記事を参照されたい
COVID-19治療薬候補化合物のリポジショニング
通常、疾患の治療薬を創薬するには10年単位の時間を要する。COVID-19の治療薬の場合には病原体であるSARS-CoV-2ウィルスの増殖(具体的には例えば体細胞への侵入阻害)を抑止する化合物を探す必要がある。その際、可溶性や、副作用などの詳細な検討を行う必要があり、これが創薬に長い年月がかかる1つの要因となっている。しかし、既知化合物が、SARS-CoV-2の増殖を効果的に抑えることができれば可溶性や副作用など薬として不可欠な性質の多くが確認済みであるため、創薬期間の大幅な短縮が可能になる。現在、COVID-19は世界中で多くの人々の生活に深刻な影響を与えていうため、早期の開発求められており、この観点から既存薬剤のリポジショニングは大きな期待を集めている。
本研究ではSARS-CoV-2をヒトの肺から作った培養細胞に感染させた際に発現が変化する遺伝子をまずテンソル分解を用いた教師無し学習による変数選択法で選択した後、これらの遺伝子をcというエンリッチメントサーバーにアップロードして、これらの遺伝子を標的とsする既知化合物を選択することでリポジショニングを実行する。
感染細胞の実験データへのテンソル分解を用いた教師無し学習による変数選択法の適用
感染細胞の遺伝子発現プロファイルはは$x_{ijkm} \in \mathbb{R}^{N \times 5 \times 2 \times 3}$という形のテンソルの形式にフォーマットできるような形式で与えられている。ここで$i$は遺伝子を、$j$は培養細胞の種類を、$k$は感染の有無を、そして$m$は3つのBiological replicateを表している。$N$は遺伝子の総数である。これを
$$
x_{ijkm} = \sum_{j=1}^5 \sum_{k=1}^2 \sum_{m=1}^3 \sum_{i=1}^N G(\ell_1 \ell_2 \ell_3 \ell_4) u_{\ell_1 j} u_{\ell_2 k} u_{\ell_3 m} u_{\ell_1 i}
$$
とテンソル分解する。$G \in \mathbb{R}^{5 \times 2 \times 3 \times N}$はコアテンソル、$u_{\ell_1 j} \in \mathbb{R}^{5 \times 5},
u_{\ell_2 k} \in \mathbb{R}^{2 \times 2}, u_{\ell_3 m} \in \mathbb{R}^{3 \times 3}, u_{\ell_1 i} \in \mathbb{R}^{N \times N}$は、特異値行列で直交行列である。ここで我々は「培養細胞にもbiological replicateにもよらず、感染と非感染で発現差がある遺伝子」を見つけたい。この様な依存性を表現する特異値ベクトルは$u_{\ell_1j}$と$u_{\ell_3 m}$が$j$や$m$によらず、$u_{\ell_21} = - u_{\ell_2 2}$であるような$\ell_1,\ell_2,\ell_3$である。
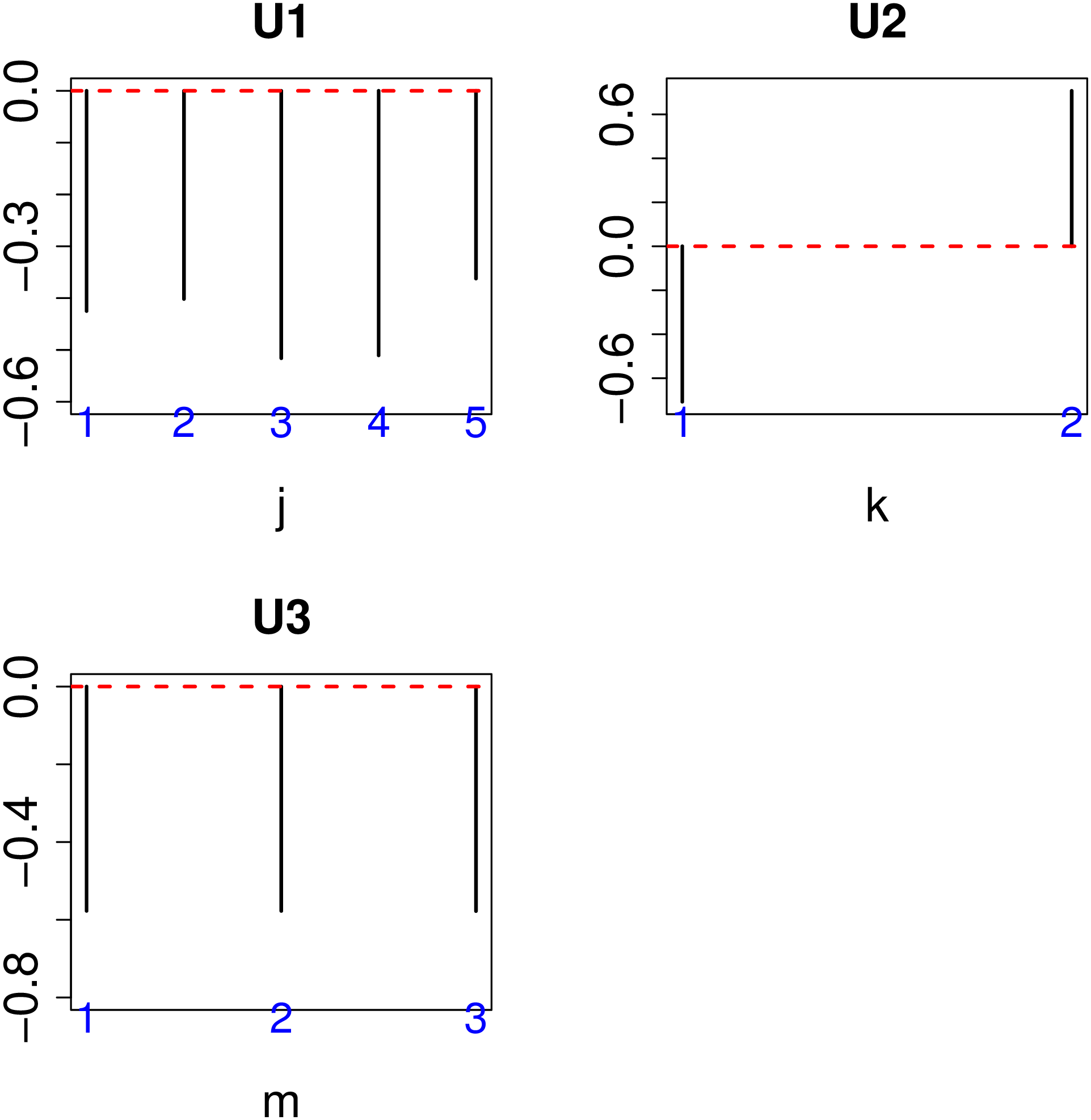
このような$\ell_1,\ell_2,\ell_3$は上図の様に$\ell_1=\ell_3=1,\ell_2=1$であることがわかる。そこでこれら絶対値の大きな$G$を共有する$\ell_4$をみつければ対応する$u_{\ell_4 i}$の絶対値が大きい遺伝子$i$ほそ「培養細胞にもbiological replicateにもよらず、感染と非感染で発現差がある遺伝子」であると言える。
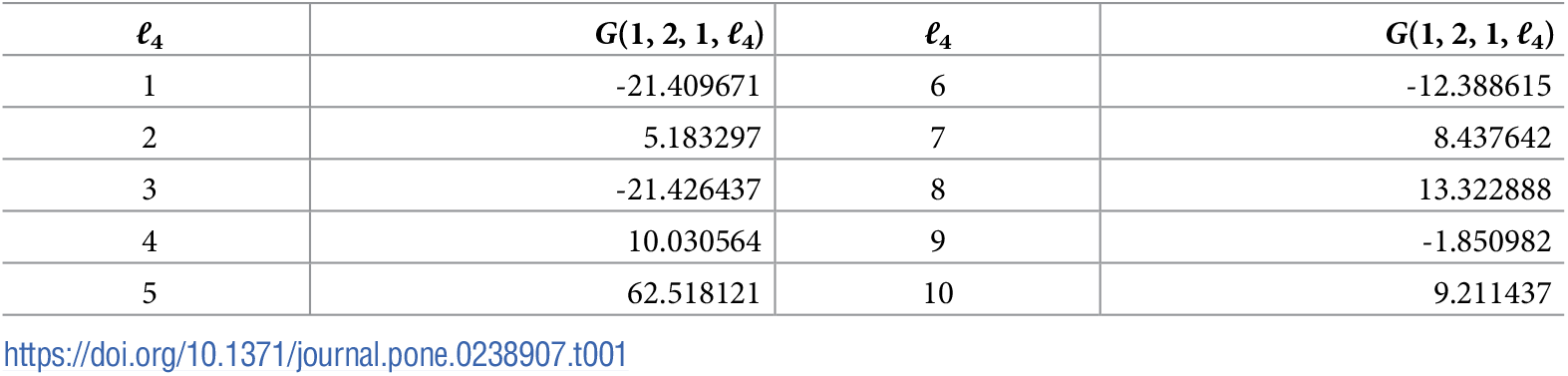
上表より分かるようにこの様な$\ell_4$は$\ell_4=5$であることが分かる。したがって、$u_{\ell_4 i}$の絶対値が有意に大きい$i$を探せばよい。ここでは帰無仮説として$u_{\ell_4 i}$はガウス分布であると仮定して累積χ二乗分布$P_{\chi^2}[>x]$を用いて$P$値を
$$
P_i= P_{\chi^2} \left [ > \left( \frac{u_{5i}}{\sigma_5}\right)^2 \right]
$$
で$i$に付与する。ここで$\sigma_5$は標準偏差である。$P_i$はBenjamini-Hochberg 法で多重比較補正し、補正$P$値が0.01以下の遺伝子163個を選択した。

これらがテンソル分解を用いた教師無し学習による変数選択法で選んだ「培養細胞にもbiological replicateにもよらず、感染と非感染で発現差がある遺伝子」であると予想される。
選択遺伝子の生物学的な評価
まずはテンソル分解を用いた教師無し学習による変数選択法でいくつかの評価を行った。まずは“Virus-Host PPI P-HIPSTer 2020”というウィルス遺伝子と相互作用することが知られている遺伝子とのオーバーラップを見た(S1 Table)。残念ながら、SARS-CoV-2のデータはEnrichrにはないがSARSなどの近縁のウィルスの遺伝子と相互作用することが知られているヒト遺伝子と広範にオーバーラップしてしていることが分かる。これだけでも十分なのであるが、更に、“Virus Perturbations from GEO up” (S2 Table)と“Virus Perturbations from GEO down” ([S3 Table](“Virus Perturbations from GEO down” (S3 Table)とのオーバーラップを見た。これらはウィルス感染時に発現が変化する遺伝子である。やはりSARS-CoV-2はないがSARSなどの近縁のウィルス感染時に発現が変化する遺伝子と大きくオーバーラップしている。最後にSARS-CoV-2の遺伝子と相互作用することが知られているヒト遺伝子を見てみた(Table S33)。すべてのSARS-CoV-2遺伝子と相互作用するヒト遺伝子と非常に広範にオーバーラップしている。これらの評価からテンソル分解を用いた教師無し学習による変数選択法はSARS-CoV-2感染に関係するヒト遺伝子を高精度で選択したと言える
ドラッグリポジショニング
次にこれらの163遺伝子の発現量を大きく変化させる化合物を探すことでドラッグリポジショニングを行う。幸いにもEnrichrには多種類の化合物投与時に発現が変化する遺伝子のデータがたくさん収容されている。全体像は論文を見ていただけばいいが、非常に多数個の既知の抗ウィルス薬がヒットしていることがわかる。実際、SARS-CoV-2の候補薬として提案されている薬がたくさん含まれているのである(Table S34)。
最後に1つだけよく知られている例をあげる。それはイベルメクチンである。イベルメクチンはもともとノーベル賞受賞者の大村教授が寄生虫薬として発見したものであるが、現在、日本でコロナ治療薬としての治験が開始されている。このイベルメクチンは我々の手法が検出した候補化合物に含まれていた(Table 3)。
またここ最近イベルメクチンの有効性をうたうプレプリントが投稿された。
この様に我々が見つけた候補化合物は非常に多くの有望なCOVID-19治療薬候補の化合物を含んでいることが期待される。
おわりに
テンソル分解を用いた教師無し学習による変数選択法は感染時に発現が大きく変化する遺伝子を選び、投与時にそれらの遺伝子を大きく変化させる化合物を選ぶという非常に単純なスキームでCOVID-19の治療薬候補化合物を推定できる優れた方法であることが分かった。