概要
以前、GNUのMIPソルバー「GLPK」についての解説記事を作成しました。
GLPK for C#/CLIで遊ぼう!
GLPKを手頃に扱えるラッパークラスを作成しました
また、ソルバーライブラリ「Microsoft Solver Foundation」についての解説記事も書きました。
Microsoft Solver Foundationを使ってみる
今回の記事では、よりモダン・高速なライブラリである「Google Optimization Tools」についての解説を行います。
導入方法
まず、公式サイトからzipをダウンロードしてください。
Visual Studio 2017の場合、2017/09/29時点で「or-tools_VisualStudio2017-64bit_v6.4.4495.zip」を落とせば大丈夫です。
なお、ソースコードおよびリリースバイナリ全部にアクセスしたい場合は、GitHubの当該ページに当たると良いでしょう。
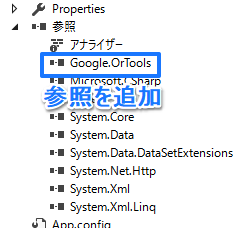
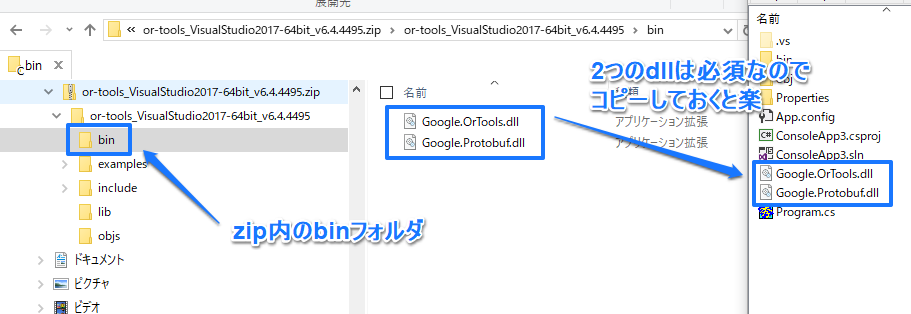
次に普通にVS上でプロジェクトを作成し、そこにzip内のbinフォルダにある「Google.OrTools.dll」を参照で追加します。
名前で察せられると思いますが、このバイナリはx64版しかありませんのでビルド設定に注意しましょう。
実行には「Google.Protobuf.dll」も必要ですので、プロジェクト内にコピーしておくと便利でしょう。
2017/09/29 21:19訂正:Google.Protobuf.dllは無くても実行に問題はないようです。
※以下は「Visual Studio 2017でC#を用いて開発する場合」の記述になります。不思議なことに、v6.3のzip(or-tools_VisualStudio2017-64bit_v6.3.4431.zip)だとビルドできこそすれ実行できなかったので注意が必要です
使用方法
いつものサンプル問題を定式化してみました。
- 最大化する目的関数:$Z=5X+4Y$
- 制約式1:$1.5X+3Y\leq13.5$
- 制約式2:$3X+Y\leq10$
- 制約式3:$X+2Y\geq7$
- 変数の範囲:$X\geq0$, $Y\geq0$
- その他:$X,Y\in\mathbb{N}$
using System;
using Google.OrTools.LinearSolver;
namespace ConsoleApp3 {
class Program {
static void Main(string[] args) {
// 解く問題を初期化(IDisposable対応)
// ・線形計画法/整数計画法なので"IntegerProgramming"
// ・ソルバーとしてCoin-or branch and cut(CBC)を使うので"CBC_MIXED_INTEGER_PROGRAMMING"
// ※ソルバーにGlop(”GLOP_LINEAR_PROGRAMMING”)を指定すると、整数制約が守られないので注意
using (var solver = Solver.CreateSolver("IntegerProgramming", "CBC_MIXED_INTEGER_PROGRAMMING")) {
// 初期化できてない場合はnullが返る
if (solver == null) {
Console.WriteLine("ソルバーを初期化できませんでした。");
return;
}
// 最適化の方向を設定する
// 最大化→SetMaximization、最小化→SetMinimization
var objective = solver.Objective();
objective.SetMaximization();
// 制約式の数・範囲
var e1 = solver.MakeConstraint(double.NegativeInfinity, 13.5);
var e2 = solver.MakeConstraint(double.NegativeInfinity, 10.0);
var e3 = solver.MakeConstraint(7.0, double.PositiveInfinity);
// 変数の数・名前・範囲
// 実数→MakeNumVar、整数→MakeIntVar、0-1変数→MakeBoolVar
// (0-1変数以外だと、下限および上限を指定できる)
// なお、MakeVarだと引数で整数制約があるか否かをbool指定できる
var x = solver.MakeIntVar(0.0, double.PositiveInfinity, "X");
var y = solver.MakeIntVar(0.0, double.PositiveInfinity, "Y");
// 目的関数の係数
objective.SetCoefficient(x, 5);
objective.SetCoefficient(y, 4);
// 制約式の係数
e1.SetCoefficient(x, 1.5);
e1.SetCoefficient(y, 3);
e2.SetCoefficient(x, 3);
e2.SetCoefficient(y, 1);
e3.SetCoefficient(x, 1);
e3.SetCoefficient(y, 2);
// 最適化
int resultStatus = solver.Solve();
// 結果表示
// 結果の返り値はdoubleなので注意
if (resultStatus != Solver.OPTIMAL) {
Console.WriteLine("ソルバーで解けませんでした。");
return;
}
Console.WriteLine($"計算時間:{solver.WallTime()}[ms]");
Console.WriteLine($"Z = {solver.Objective().Value()}");
Console.WriteLine($"{x.Name()} = {x.SolutionValue()}");
Console.WriteLine($"{y.Name()} = {y.SolutionValue()}");
}
return;
}
}
}
GLPKやMicrosoft Solver Foundationと異なり、「変数」「制約式」をGoogle.OrTools.LinearSolver.Variable型およびGoogle.OrTools.LinearSolver.Constraint型として指定しますので、より直感的に問題を構成することができます。
また、Make○○VarArrayメソッドやMake○○VarMatrixメソッドを使うことで、問題に使用する変数を1次元配列・2次元配列として確保・初期化することができます。
更に、計算速度も(無償で使える中では)高速なようです。今後は積極的に利用していきたいですね。
……フットプリントがかなり大きいけどな(GLPKで2MB,MSFで2.5MBなのに17MB近くもある)