GLPK for C#/CLIで遊ぼう！

目次

• 第1章では、GLPKについての簡単な説明を行います。
• 第2章では、例題をベースに、GLPKのAPIをざっくりと学びます。
• 第3章では、GLPKについての補足説明を行います。
• 第4章では、第2章で説明していなかったAPIについて軽く触れます。

第1章　概要

　何かを最適化したい、と思ったことはありませんか？
　最適化問題には様々な種類がありますが、今回紹介するGLPKは、その中の混合整数計画問題を解くためのソルバーの1つです。詳しくは、次の関連記事をご覧ください。

　MIP(混合整数計画問題)ソルバーを作ろう！ - Qiita

GLPKとは

　GNU Linear Programming Kitの通称です。
　名前の通りGNUプロジェクトの1つで、GPL v3.0によりライセンスされています。
　本体はANSI Cで書かれており、次のような機能を持つとReadmeに書かれています。

• 線形計画問題向け
• シンプレックス法(2段階法にも対応)
• 内点法
• 整数計画問題向け
• 分枝限定法
• 利用方法
• 各種API(C言語・Java・C#向け)
• モデリング言語(MathProg)
• スタンドアロンなソルバー(GLPSOL)

　性能は……ベンチマーク結果からお察しください

GLPK for C#/CLIとは

　C#でもGLPKを使えるようにするためのライブラリです。
　より詳しく言えば、次の3種類のファイルを組み込むだけでOKです。

• glpk_X_YZ.dll……C言語で叩く際の本体。Ver.4.61ならglpk_4_61.dllとなる
• libglpk_cli_native.dll……C++/CLIで叩く際に組み込むのでしょう、たぶん
• libglpk-cli.dll……C#で叩く際に組み込む(プロジェクトの参照に追加する)

　GPLKにおける各種関数はorg.gnu.glpk名前空間内に配置されており、それを叩くことで利用できます。
　ただ、APIの仕様がGLPKを思いっきり引きずったものになっているのが厄介なところ。
　先述のようにC言語で書かれたC言語用のライブラリですので、APIもC言語流なのです。
　その結果、オブジェクト指向言語用のライブラリとは思えないメソッド群を操ることに……。

　第2章以下は覚悟してお読みください。

第2章　GLPKのAPIについて

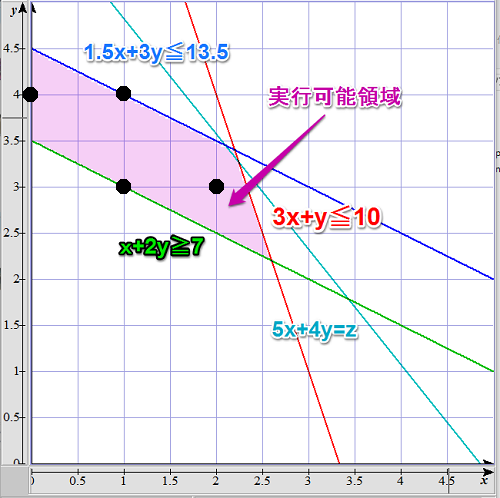
　今回解く問題は、以前解説したこれです。
　紫色に塗りつぶした領域が実行可能領域で、黒い点が整数条件を満たす解です。

• 最大化する目的関数：$Z=5X+4Y$
• 制約式1：$1.5X+3Y\leq13.5$
• 制約式2：$3X+Y\leq10$
• 制約式3：$X+2Y\geq7$
• 変数の範囲：$X\geq0$,　$Y\geq0$
• その他：$X,Y\in\mathbb{N}$

問題を設定

まず、プロジェクトの参照にlibglpk-cli.dllを追加した上で、次の名前空間をusing宣言します。
　using org.gnu.glpk;
次に、問題を定義するためのクラスのインスタンスを作成します。
コンストラクタではなく専用の関数で作成するところからクｓ……歴史の長さが滲み出ていますね。
(※流石に型推論は効きますが、説明のため、サンプルコードでvarは使用しないようにしました)
　glp_prob mip = GLPK.glp_create_prob();
次に、目的関数を最適化する方向を決めます。最大化問題ならGLPK.GLP_MAX、最小化問題ならGLPK.GLP_MINです。
　GLPK.glp_set_obj_dir(mip, GLPK.GLP_MAX);
次に、制約式と変数の数を決めます。「row」が制約式の数、「col」(column)が変数の数を表します。
　GLPK.glp_add_rows(mip, 3);
　GLPK.glp_add_cols(mip, 2);
次に、それぞれの制約式と変数にについて、上限と下限の範囲を設定します。
「制約式に範囲？」と思われるかもしれませんが、要するに次のような理屈です。

• $1.5X+3Y\leq13.5$なら、「$P=1.5X+3Y$」が「$P\leq13.5$」であると考える
• $X+2Y\geq7$なら、「$Q=X+2Y$」が「$Q\geq7$」であると考える

ただ、上限と下限の範囲の設定が5通りもあるので、適宜使い分けましょう。
また、**C言語用のAPIなのになぜか1オリジン**なので、設定する際にはミスらないように気をつけましょう。

• GLPK.GLP_UP→上限のみ定める。「$-\infty\leq P\leq10$」など
• GLPK.GLP_LO→下限のみ定める。「$-5\leq P\leq\infty$」など
• GLPK.GLP_DB→両方定める。「$-1\leq P\leq1$」など
• GLPK.GLP_FR→両方定めない。つまり「$\infty\leq P\leq\infty$」
• GLPK.GLP_FX→両方が同じ値。つまり「$P=2$」など

　GLPK.glp_set_row_bnds(mip, 1, GLPK.GLP_UP, 0.0, 13.5);
　GLPK.glp_set_row_bnds(mip, 2, GLPK.GLP_UP, 0.0, 10.0);
　GLPK.glp_set_row_bnds(mip, 3, GLPK.GLP_LO, 7.0, 0.0);
　GLPK.glp_set_col_bnds(mip, 1, GLPK.GLP_LO, 0.0, 0.0);
　GLPK.glp_set_col_bnds(mip, 2, GLPK.GLP_LO, 0.0, 0.0);

次に、目的関数の係数を決定します。

　GLPK.glp_set_obj_coef(mip, 1, 5.0);
　GLPK.glp_set_obj_coef(mip, 2, 4.0);

次に、変数に整数制約を設定します。未設定かGLP_CVと設定すると連続変数、GLP_BVと設定するとバイナリ変数扱いになります。

　GLPK.glp_set_col_kind(mip, 1, GLPK.GLP_IV);
　GLPK.glp_set_col_kind(mip, 2, GLPK.GLP_IV);

次に、制約式の(左辺における)係数を決定します。
1行・1列の単位で変更する関数としてはglp_set_mat_rowやglp_set_mat_colがあります。
……が、ここは一度に全てを書き換えてみましょう。まず、行番号・列番号・係数を保存する配列を用意します。
3制約式・2変数ですので用意するべき領域は3×2＝6個ですね。

　SWIGTYPE_p_int ia = GLPK.new_intArray(6 + 1);
　SWIGTYPE_p_int ja = GLPK.new_intArray(6 + 1);
　SWIGTYPE_p_double ar = GLPK.new_doubleArray(6 + 1);

**ここで混乱してきたあなたの脳は正常です。**酷いことは更に続きます。何と、代入にすら特殊な関数を要するのです！

　GLPK.intArray_setitem(ia, 1, 1);　//行番号を代入
　GLPK.intArray_setitem(ia, 2, 1);
　GLPK.intArray_setitem(ia, 3, 2);
　GLPK.intArray_setitem(ia, 4, 2);
　GLPK.intArray_setitem(ia, 5, 3);
　GLPK.intArray_setitem(ia, 6, 3);
　GLPK.intArray_setitem(ja, 1, 1);　//列番号を代入
　GLPK.intArray_setitem(ja, 2, 2);
　GLPK.intArray_setitem(ja, 3, 3);
　GLPK.intArray_setitem(ja, 4, 1);
　GLPK.intArray_setitem(ja, 5, 2);
　GLPK.intArray_setitem(ja, 6, 3);
　GLPK.doubleArray_setitem(ar, 1, 1.5);　//係数を代入
　GLPK.doubleArray_setitem(ar, 2, 3.0);
　GLPK.doubleArray_setitem(ar, 3, 3.0);
　GLPK.doubleArray_setitem(ar, 4, 1.0);
　GLPK.doubleArray_setitem(ar, 5, 1.0);
　GLPK.doubleArray_setitem(ar, 6, 2.0);

つまり、「setitem(変数名, インデックス(1オリジン), 値)」は、「変数[インデックス]=値」と等価です。
更に、ia[k]行ja[k]列(ia番目の制約式のja番目の変数)の係数は「ar[ia[k]][ja[k]]=係数」と等価です。
(でも実際には[]は定義されてないけどな！)
これだけではまだ分かりづらいので、より分かりやすくするために表を用意しました(伝われ)。

係数	ia[k]	1列目(X)	2列目(Y)
ja[k]	―	1	2
1行目	1	k=1,ar=1.5	k=2,ar=3.0
2行目	2	k=3,ar=3.0	k=4,ar=1.0
3行目	3	k=5,ar=1.0	k=6,ar=2.0

最後に、係数をまとめて設定すればひとまず完了です。お疲れ様でした。
　GLPK.glp_load_matrix(mip, 6, ia, ja, ar);

問題を解く・結果を表示する

線形計画問題の場合

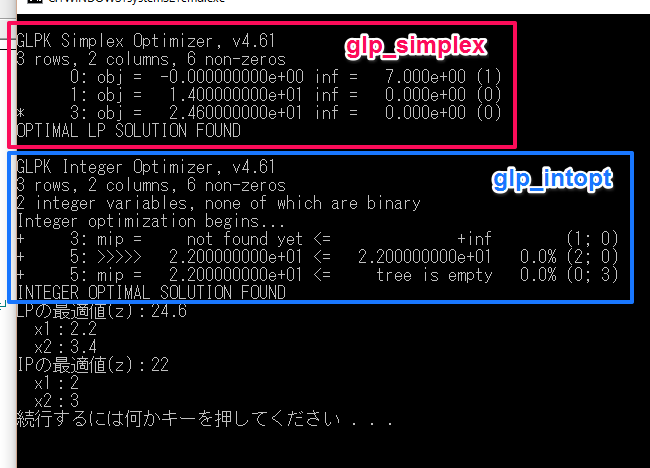
glp_simplex関数を使います。とりあえず解くだけなら次のように書くだけでOKです。
　int result = GLPK.glp_simplex(mip, null);
ただ、第二引数には、解く際の条件を色々と記述することができます(詳しくは第3章で解説)。
また、関数の返り値には、問題が解けたかどうかの情報が返ってきます(詳しくは第3章で解説)。
　解いた後、目的関数の値はglp_get_obj_val関数、各変数の値はglp_get_col_prim関数で取得できます。

　double z = GLPK.glp_get_obj_val(mip);
　double x1 = GLPK.glp_get_col_prim(mip, 1);
　double x2 = GLPK.glp_get_col_prim(mip, 2);

混合整数計画問題の場合

ざっくり言えば、名前が次のように置き換わるだけです。
(最初にこれを知った際は命名規則もあったもんじゃねえなと思いましたが)

• glp_simplex→glp_intopt
• glp_get_obj_val→glp_mip_obj_val
• glp_get_col_prim→glp_mip_col_val

ただし、glp_intopt関数はglp_simplex関数を呼んだ後でしか使えません。
つまり、glp_get_obj_valを叩けば「緩和問題の最適値」、glp_mip_obj_valなら「本来の問題の最適値」が分かるわけです。

後片付け

　問題を解き終わった後は明示的に破棄しましょう。コイツにGCは効きません。

GLPK.delete_intArray(ia);
GLPK.delete_intArray(ja);
GLPK.delete_doubleArray(ar);
GLPK.glp_delete_prob(mip);

2017/02/09追記：
　実装を確認した所、org.gnu.glpk.glp_probクラスはIDisposableを継承しており、またデストラクタも実装されているので、glp_delete_probしなくてもいいと思われます。ただ、コンストラクタがコンストラクタしてないというクソ仕様があるので、デストラクタもロクな実装がない可能性があるのがフフ怖……
　あ、SWIGTYPE_p_intとSWIGTYPE_p_doubleにはデストラクタの痕跡もないよ！制作者の悪意を感じるね！

サンプルコード

　上記全てを盛り込んだサンプルコードをアップロードしておきます。
　　https://gist.github.com/YSRKEN/b17d99d54d2001d3d152ac78a8755f63

第3章　補足説明

上記だけの知識で計算させると、標準出力に解の状況が表示されるといった問題が起きます。
これは、シンプレックス法や分枝限定法などで解かせる関数が、標準でそんな仕様になっているからです。

これを修正するには、第二引数にnullではなく、glp_smcp構造体(glp_simplexの場合)かglp_iocp構造体(glp_intopt)をあてがう必要があります。
構造体なので謎の初期化関数も破棄関数も不要です(C#で言えば単にnewするだけ)……と言いたいところでしたが、
やっぱり謎の初期化関数(glp_init_smcpとglp_init_iocp)が付いてきたよ！やったね！！！ /* ヤケクソ */

//LP
　glp_smcp smcp = new glp_smcp();
　GLPK.glp_init_smcp(smcp);
　smcp.msg_lev = GLPK.GLP_MSG_OFF; //標準出力をOFFにする
//MIP
　glp_iocp iocp = new glp_iocp();
　GLPK.glp_init_iocp(iocp);
　iocp.msg_lev = GLPK.GLP_MSG_OFF; //標準出力をOFFにする

ここで注目すべきはmsg_levプロパティ。ここにGLPK.GLP_MSG_OFFを代入すれば、状況が標準出力に出てくることはなくなります。
他にも多数の設定事項がありますが、気になる人は参考資料のGLPKリファレンスを読んでください。

また、glp_simplex関数やglp_intopt関数の返り値から、問題が解けたかどうかを判断できます。
(「意味」の部分の訳はGoogle翻訳頼りなので、どなたか詳しい方はご教示いただけると助かります)

返り値	意味	LP	MIP
0	正常に解くことができた	○	○
GLPK.GLP_EBADB	制約式に不備がある	○
GLPK.GLP_ESING	基底行列が計算精度内で特異だ	○
GLPK.GLP_ECOND	基底行列の条件数が大きすぎる	○
GLPK.GLP_EBOUND	変数の範囲設定に誤りがある	○	○
GLPK.GLP_EFAIL	ソルバーに障害が発生した	○	○
GLPK.GLP_EITLIM	反復回数の制限を超えた	○
GLPK.GLP_ETMLIM	計算時間の制限を超えた	○	○
GLPK.GLP_EMIPGAP	ギャップが公差に達したので早期に終了した		○

第4章　情報取得用APIについて

　GLPKにはglp_probをファイル出力するAPIはあるのに中身をテキスト表示するAPIはありません。
　その時点で頭がクラクラしてきますが、もっと酷いのはGLPK for C#/CLIでもそれが同様ということです。
(ヘルパー関数ぐらい付けろよ！何のためにgetterがあると思っていやがる！)
　というわけで、中身をLPファイル形式で表示するためのコードを書いてみました。

目的関数

　最適化する方向はglp_get_obj_dir関数、変数の数はglp_get_num_cols関数、目的関数の係数はglp_get_obj_coef関数で取得できます。ここはまだ、「getの反対はset」程度の話ですので分かりやすいでしょう。

lp_file += (GLPK.glp_get_obj_dir(mip) == GLPK.GLP_MIN ? "minimize" : "maximize") + "\n";
var colCount = GLPK.glp_get_num_cols(mip);
for(int i = 1; i <= colCount; ++i) {
	var coef = GLPK.glp_get_obj_coef(mip, i);
	lp_file += " " + (coef >= 0.0 ? "+" : "") + coef.ToString() + " x" + i.ToString();
}
lp_file += "\n";

制約式

　ここが一番の難所です。制約式の数はglp_get_num_rows関数、係数はglp_get_mat_row関数で1制約式毎に取得できる……のですが、注目したいのはこれが疎行列を意識しているということです。
　一般に、解かれる制約式の係数は殆どが0だったりします。それなのにバカ正直に「変数の数×制約式の数」だけの係数の配列を確保すると、メモリが非常にもったいないという問題があります。
　そこで、「添字と値のセット」を配列でそれぞれ管理することにより省メモリを図る……これが、第2章の説明でiaとjaとarが別々に用意されている理由です。
　具体的には、GLPK.glp_get_mat_row(mip, i, null, null)と唱えると、返り値が「その制約式の左辺における非0係数の数」となります。で、ind GLPK.new_intArrayやval = GLPK.new_doublerrayで確保した後、今度はGLPK.glp_get_mat_row(mip, i, ind, val)と唱えると、欲しい係数の添字と値が配列で手に入るという理屈です。
　また、glp_get_row_typeは制約式の範囲についての情報が手に入りますが、ここでGLPK.GLP_UPとかが定数扱いではないのでswitch文で使えないというクソな仕様が判明しました。アイエエエ！？ナンデ！？
(glp_get_col_lbとglp_get_col_ubで上限と下限が得られる)

lp_file += "subject to\n";
var rowCount = GLPK.glp_get_num_rows(mip);
var ind = GLPK.new_intArray(colCount + 1);
var val = GLPK.new_doubleArray(colCount + 1);
for(int i = 1; i <= rowCount; ++i) {
	var subject = "";
	var len1 = GLPK.glp_get_mat_row(mip, i, null, null);
	var len = GLPK.glp_get_mat_row(mip, i, ind, val);
	var coef = new List<double>();
	for(int j = 0; j < colCount; ++j) {
		coef.Add(0.0);
	}
	for(int j = 1; j <= len; ++j) {
		coef[GLPK.intArray_getitem(ind, j) - 1] = GLPK.doubleArray_getitem(val, j);
	}
	for(int j = 0; j < colCount; ++j) {
		subject += " " + (coef[j] >= 0.0 ? "+" : "") + coef[j].ToString() + " x" + (j + 1).ToString();
	}
	var type = GLPK.glp_get_row_type(mip, i);
	var lb = GLPK.glp_get_row_lb(mip, i);
	var ub = GLPK.glp_get_row_ub(mip, i);
	if(type == GLPK.GLP_FR) {
		//
	}else if(type == GLPK.GLP_LO) {
		lp_file += subject + " >= " + lb;
	}else if(type == GLPK.GLP_UP) {
		lp_file += subject + " <= " + ub;
	}else if(type == GLPK.GLP_DB) {
		lp_file += subject + " >= " + lb + "\n";
		lp_file += subject + " <= " + ub;
	} else {
		lp_file += subject + " = " + lb;
	}
	lp_file += "\n";
}

変数制約

　制約式の地獄を抜けられた人なら以降は楽勝でしょう。glp_get_col_typeのようにrowとcolとを入れ替えた関数と、変数の種類についての情報を得るためのglp_get_col_kind関数があります。

lp_file += "bounds\n";
for(int i = 1; i <= colCount; ++i) {
	var type = GLPK.glp_get_col_type(mip, i);
	var lb = GLPK.glp_get_col_lb(mip, i);
	var ub = GLPK.glp_get_col_ub(mip, i);
	if(type == GLPK.GLP_FR) {
		lp_file += "x" + i.ToString() + " free";
	} else if(type == GLPK.GLP_LO) {
		lp_file += "x" + i.ToString() + " >= " + lb;
	} else if(type == GLPK.GLP_UP) {
		lp_file += "x" + i.ToString() + " <= " + ub;
	} else if(type == GLPK.GLP_DB) {
		lp_file += " " + lb + " <= x" + i.ToString() + " <= " + ub;
	} else {
		lp_file += "x" + i.ToString() + " = " + lb;
	}
	lp_file += "\n";
}
lp_file += "general\n";
for(int i = 1; i <= colCount; ++i) {
	var type = GLPK.glp_get_col_kind(mip, i);
	if(type == GLPK.GLP_IV) {
		lp_file += " x" + i;
	}
}
lp_file += "\n";
lp_file += "binary\n";
for(int i = 1; i <= colCount; ++i) {
	var type = GLPK.glp_get_col_kind(mip, i);
	if(type == GLPK.GLP_BV) {
		lp_file += " x" + i;
	}
}
lp_file += "\n";

サンプルコード

　上記全てを盛り込んだサンプルコードをアップロードしておきます。
　　https://gist.github.com/YSRKEN/18e785f2ae2a886891718b41e125dcba

参考資料

• GLPKのリファレンス