概要
以前、GNUのMIPソルバー「GLPK」についての解説記事を作成しました。
GLPK for C#/CLIで遊ぼう!
GLPKを手頃に扱えるラッパークラスを作成しました
ですが、これ以外にもタダで使えるソルバーライブラリの1つとして、「Microsoft Solver Foundation」というソルバーライブラリがあることを知りました。以下、簡単な使い方を解説します。
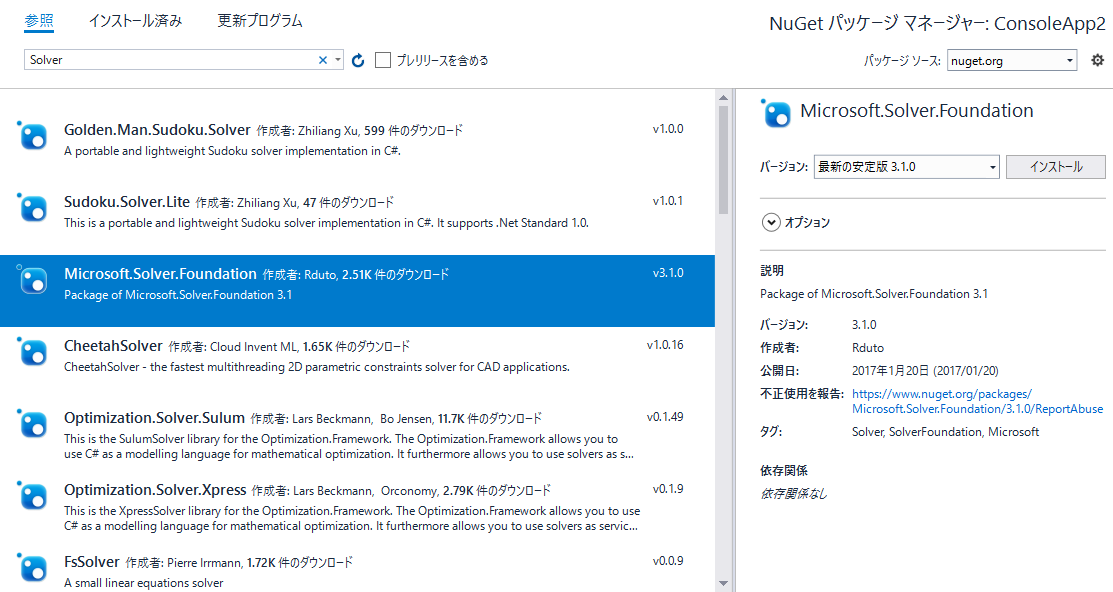
導入方法
Nugetから簡単にダウンロードできます。
使用方法
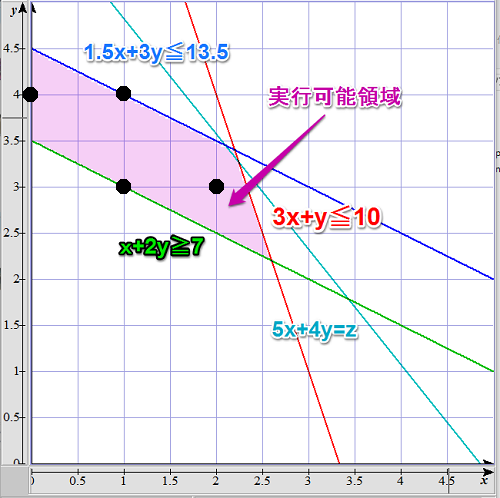
いつものサンプル問題を定式化してみました。
- 最大化する目的関数:$Z=5X+4Y$
- 制約式1:$1.5X+3Y\leq13.5$
- 制約式2:$3X+Y\leq10$
- 制約式3:$X+2Y\geq7$
- 変数の範囲:$X\geq0$, $Y\geq0$
- その他:$X,Y\in\mathbb{N}$
using System;
using System.Linq;
using Microsoft.SolverFoundation.Solvers;
namespace ConsoleApp2 {
class Program {
static void Main(string[] args) {
// 解く問題を初期化(IDisposableではない)
var solver = new SimplexSolver();
// 使用する変数のID・制約式のID・目的関数のIDを宣言する
int x, y, z = 0, e1, e2, e3;
// 最適化の方向を設定する
// AddGoal(目的関数の数値が代入される変数のID, (不明), 最大化するならfalse・最小化するならtrue)
solver.AddRow("目的関数値", out z);
solver.AddGoal(z, 1, false);
// 制約式の数・名前・範囲
solver.AddRow("条件1", out e1);
solver.AddRow("条件2", out e2);
solver.AddRow("条件3", out e3);
solver.SetBounds(e1, double.NegativeInfinity, 13.5);
solver.SetBounds(e2, double.NegativeInfinity, 10.0);
solver.SetBounds(e3, 7.0, double.PositiveInfinity);
// 変数の数・名前・範囲
// SetIntegralityメソッドで整数条件を付与できることがポイント
solver.AddVariable("X", out x);
solver.AddVariable("Y", out y);
solver.SetBounds(x, 0.0, double.PositiveInfinity);
solver.SetBounds(y, 0.0, double.PositiveInfinity);
solver.SetIntegrality(x, true);
solver.SetIntegrality(y, true);
// 目的関数の係数
solver.SetCoefficient(z, x, 5);
solver.SetCoefficient(z, y, 4);
// 制約式の係数
solver.SetCoefficient(e1, x, 1.5);
solver.SetCoefficient(e1, y, 3);
solver.SetCoefficient(e2, x, 3);
solver.SetCoefficient(e2, y, 1);
solver.SetCoefficient(e3, x, 1);
solver.SetCoefficient(e3, y, 2);
// 最適化
solver.Solve(new SimplexSolverParams());
// 結果表示
// GetValueメソッドの返り値はRational型……要するに分数なので、
// ToDouble()メソッドでdouble型にすると分かりやすい
Console.WriteLine($"Z = {solver.GetValue(z).ToDouble()}");
for (int i = 0; i < solver.VariableCount; ++i) {
int valueId = solver.VariableIndices.ElementAt(i);
string valueName = (string)solver.VariableKeys.ElementAt(i);
Console.WriteLine($"{valueName} = {solver.GetValue(valueId).ToDouble()}");
}
}
}
}
GLPKの奴よりは自然なインターフェースな気がします。変数・目的関数値・制約式それぞれに整数の「ID」を割り当てるのだ、ということが分かれば読み解くのは容易いでしょう。また、ソルバーでの計算結果の返り値がdoubleではなくRational型なのも(計算精度的な意味で)興味深いところです。
……ただ、計算速度が遅いといった報告があるのがソルバーとして致命的な気もしますorz