More than 1 year has passed since last update.

【AtCoder】ABC277のA,B,C,D における Python解説

Last updated at 2022-12-07Posted at 2022-12-07

ABC277のA,B,C,D問題を解くために考えたこと、ACできるPython3(PyPy3)コードを紹介します。

この記事は @u2dayo さんの記事を参考にしています。見たことのない方はそちらもご覧ください。とても勉強になります。

また、diffは問題の難易度を表す指標です。Atcoder Problems から引用しています。このサイトは勉強した問題を管理するのにとてもオススメです。

質問やご指摘はこちらまで
Twitter : Waaa1471

作者プロフィール
Atcoder ：緑 829
22/1208 現在

はじめに

特にC問題以降になると、競技プログラミングに典型的な前提知識、少し難しい数学的考察が必要になり始めます。
しかし、公式解説ではこの部分の解説があっさりしすぎていて競技プログラミング(Atcoder)を始めたばかりの人にはわかりにくい、難しいと感じるのではないでしょうか。

またC++がわからないと、コードの書き方を勉強することが難しいです。一応、参加者全員のコードを見ること自体は可能ですが、提出コードは必ずしも教育的ではありません(ここで紹介する記事も本番で提出したものとは全く異なります)。そんなものから初学者が解説もなしになにか得ることはとても難しいと思います。実際適当に何人かのコードをみたものの、意味がわからずに終わった経験があるのではないでしょうか。

この記事がそんな方々の勉強の助けになればよいなと思っています。

A.^{-1}

問題

灰色 diff 11

考察

前から探索

「数列 P の要素のうち、値がXとなるものは前から何番目にあるか」求めればよいです。
素直に前から順に調べていけばよいでしょう。計算量はO(N)です。
また、pythonではindex番号は 0 始まりで、P の番号は1始まりです。このズレを調整する必要があります。

コード

pypy3

N,X=[int(nx) for nx in input().split()]
P=[int(p) for p in input().split()]
for i,p in enumerate(P):
    if p==X:
        print(i+1)
        exit()

補足

計算量
計算量がわからない場合はこちらの A問題の補足で説明していますのでご覧ください。

B.Playing Cards Validation

問題
灰色 diff 60

考察

以下3つの条件をすべての文字列で満たすかどうか調べます

条件1.すべての文字列に対して、1 文字目は H , D , C , S のどれかである。

条件2.すべての文字列に対して、2 文字目は A , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , T , J , Q , K のどれかである。

条件3.すべての文字列は相異なる。

条件1 , 条件2

各文字列の先頭と末尾がそれぞれ条件を満たすか調べることで判定できます。文字列の検索は in で行えます。

条件3

文字列どうしを比較します。集合で一度調べた文字列を管理し、新たな文字列がこの中にあるかどうかで判定すればよいです。

計算量

各判定操作はO(1)で行えるので、計算量はO(N)となります。

コード

pypy3

N=int(input())
S=set()
for _ in range(N):

    s=input()

    #条件1
    if s[0] not in "HDCS":
        print("No")
        exit()
    #条件2
    if s[1] not in "A23456789TJQK":
        print("No")
        exit()
    
    #条件3
    if s  in S:
        print("No")
        exit()
    
    #次の文字列の条件3の判定のために集合に追加する
    S.add(s)
    
print("Yes")

補足

計算量～リスト検索 vs 集合検索～
リストで管理するか、集合で管理するかで検索時の計算量が異なります。リストはO(要素数)で集合はO(1)です。
参考
Pythonistaなら知っておきたい計算量のはなし
 Pythonで"in list"から"in set"に変えただけで爆速になった件とその理由

C.Ladder Takahashi

問題
茶色 540

考察

グラフにおきかえて考える

この問題は階数を頂点、はしごを辺とみなした無向グラフを考えると分かりやすいです。「頂点 1から探索を始めたときに訪れることが可能な頂点のうち、最も大きなものは何か」問われています。
グラフ探索で定番の、BFS(幅優先探索) , DFS(深さ優先探索)の計算量は O(辺数) なのでこの問題を十分高速に解くことができます。

defaultdictでメモリを節約

BFS 、DFS を行う場合、頂点を管理するリストを作成することが定番ですが、今回頂点の候補は 10^9 と非常に大きいです。この頂点を全て管理するためのリストを作成することはメモリの観点からできません。

しかし、探索すべき(管理すべき)頂点は、辺がつながっている高々 2N 個のみです。これらの頂点を効率的に管理するには defaultdict が有効です。
リストで要素を初期化して、頂点をキーに、その頂点と辺でつながっている頂点を 要素(リスト) に追加してくことで、必要な頂点だけをもつグラフを作成することができます。

BFS

あとは基本に忠実にグラフを探索すればOKです。
今回は BFSで実装しています。一度訪れた頂点を管理しながら探索を効率的に進めつつ、最終的にその頂点の中で最大のものを出力します。

コード

pypy3

from collections import deque,defaultdict
N=int(input())
G=defaultdict(list)
for _ in range(N):
    a,b=[int(ab) for ab in input().split()]
    G[a].append(b)
    G[b].append(a)

que=deque()
que.append(1)
seen=set()
seen.add(1)
while que:
    now=que.popleft()
    for nex in G[now]:
        if nex not in seen:
            que.append(nex)
            seen.add(nex)

print(max(seen))

補足

BFS
BFS (幅優先探索) 超入門！〜キューを鮮やかに使いこなす〜
「 BFSとは？」がわかります
Pythonのdequeでキュー、スタック、デック（両端キュー）を扱う
deque の使い方を勉強できます。他の問題(尺取り法など)でも使う基本的なデータ構造なので絶対覚えましょう。
また、defaultdictもこの collections ライブラリをインポートすることで使えるようになります。
練習
理論をお勉強した後は、アルゴ式で必ず練習しましょう。使いこなせないと意味がないです。
DFS
DFS (深さ優先探索) 超入門！〜グラフ・アルゴリズムの世界への入口〜【前編】
「 DFSとは? 」がわかります。
defaultdict
要素を int型や、特定のデータ構造に初期化することができる辞書です。この問題はdefaultdict を扱うとても典型的な問題です。
筆者にはこれだ !! と思える使い方の記事がなかったので、自分で調べてください。

D.Takahashi's Solitaire

問題
緑色 873

考察

状況把握

サンプル 1 を用いて問題を理解しましょう。

N=9 , M=7
A= 3 0 2 5 5 3 0 6 3

まず、例えば 3 を初めに選択する場合、0番目の3 と　最後の3 のどちらを選んでも同じです。どうせ次に選ばなかった方を捨てることになります。
次に、より多くのカードを捨てるためには、他のカードから始めても捨てることができるカードを選択するべきではないことがわかります。3を選んでも 2を選んでも 3は捨てられますが、2は2から始めないと捨てられません。

このことから、初めに選ぶべきカードの候補が次の2つに絞れます。

2 : 捨てるカードの総和 = 2+3+3+3 = 11
: 残る手札のカードの総和 = 27(初期手札の総和) - 11 = 16
5 : 捨てるカードの総和 = 5+5+6+0+0 = 16
: 残る手札のカードの総和 = 27(初期手札の総和) - 16 = 11

したがって、この場合初めに 5のカードのどれかを選択することが最適です。また、6 の次に 0 のカードが捨てられることに注意しましょう。

素直に前から探索

実験から「最初に選ぶカードの候補を手札の中から昇順に選び、連続するカードがなければ次のカードを最初に選ぶカードにする 」ような処理でこの問題を解くことができそうだと考えられます。
また、同じカードは何枚あるかさえわかればよいので、手札のカードの種類を集合、それぞれの枚数をカウンターで管理します。

するとこのような実装になりそうです。

A=[int(a) for a in input().split()]
# カードの枚数を管理
X=Counter(A)
# カードの種類を管理
AA=set(A)

# 現在捨てているカードの総和を計算
tmp=0
# 手札のカードを昇順に探索
# tmp=0 のとき、最初に選ぶべき候補である
for a in sorted(AA):
    # 総和を追加
    tmp+=a*X[a]

    if (a+1)%M not in AA:

        最初に選んだカードからはtmpだけ捨てられることを記録する処理
        
        # tmp初期化
        tmp=0

この「最初に選んだカードから、tmpだけ捨てられることを記録する処理」を実装するためには、例えばリストの「最初に選んだカード番目の値」を + tmp する処理などが考えられます。しかし、これを実現するためにはその最初に選んだカードを覚えておかなくていけません。また、最初に選んだカードが問われているわけでもありません。
そこで、ここでは tmp を管理するために、a つまり捨てられる最後のカードを使うことにします。a はループ変数なのでとても使いやすいです。
さらに、制約から $ 0 <= a <10^9 $ なのでリストでの管理は難しいです。したがって、C問題同様、 defaultdictで管理することにします。

0 と M-1 両方持っている場合

この問題でいちばんややこしいケースです。例えばこんなケースが考えられます

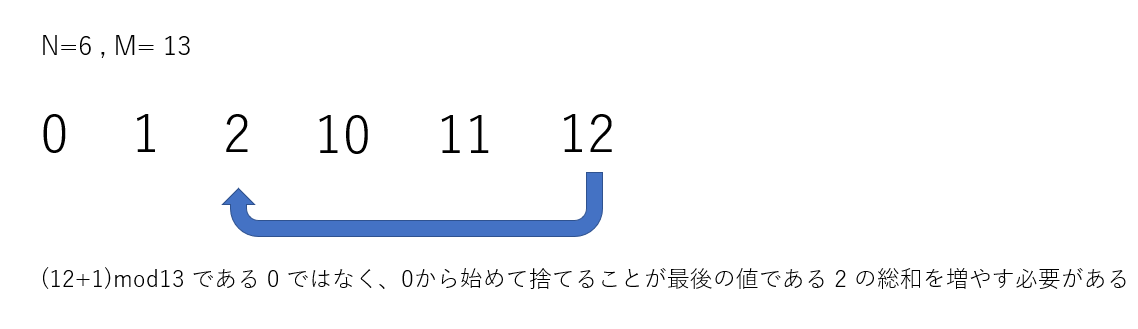
今、捨てるカードの総和を最後のカードで管理しているので、10～12 のカードの総和を 2で管理している値に追加する必要があります。

このようなMODで循環している場合には、もう一回探索する ことが解決手段として典型的です。
計算量にもほとんど影響しないので、とてもお手軽な手段です。
実装では、index番号に一致しなくなるまでカードを調べています。0 から始めて捨てることができるカードは全て 0からの連続値だからです。


# 0とM-1のカードを両方持っている場合をtmpの値で検出
# 0から始めて捨てることができる最大値にtmpを追加する必要があるのでもう一回探索する
if tmp>0:
    # 0からの連続値でなくなった場所の手前が求めるべき位置
    for i,a in enumerate(sorted(AA)):
        if i!=a:
            B[i-1]+=tmp
            break

残念ながら、このコードは想定している処理を行えていません。
なぜなら、A が 0 ～ M-1 までの全てのカードを持っている場合、tmpをどこにも追加できないからです。

この例外をうまく処理するために、手札にありえない巨大な値を持つカードをあらかじめ追加しておけばよいです。そうすれば必ず連続でないカードが検出され tmpが追加されることになります。

あとは、捨てるカードの総和から残りの手札の総和を求めて、それらの最小値を出力すればよいです。

コード

pypy3

from collections import defaultdict,Counter
N,M=[int(nm) for nm in input().split()]
A=[int(a) for a in input().split()]
# カードの枚数を管理
X=Counter(A)
# カードの種類を管理
AA=set(A)
# あるカードを捨てることで捨てられるようになる最大値を管理
B=defaultdict(int)

# 現在捨てているカードの総和を計算
tmp=0
# 手札のカードを昇順に探索
# tmp=0 のとき、最初に選ぶべき候補である
for a in sorted(AA):
    tmp+=a*X[a]
    #　グループ終了
    if (a+1)%M not in AA:
        B[a%M]=tmp
        tmp=0

# 0とM-1のカードを両方持っている場合をtmpの値で検出
# 0から始めて捨てることができる最大値にtmpを追加する必要があるのでもう一回探索する
if tmp>0:
    # 0からM-1までの全てのカードを持っている場合を考慮し、あり得ない巨大なカードを持っておく
    AA.add(10**10)

    # 0からの連続値でなくなった場所の手前が求めるべき位置
    for i,a in enumerate(sorted(AA)):
        if i!=a:
            B[i-1]+=tmp
            break

accA=sum(A)
ans=10**20
for b in B:
    # 手札のカードの総和 = 最初の総和 - 捨てたカードの総和
    ans=min(ans,accA-B[b])

print(ans)

コメントアウトが多いので、念のためコメントアウトなしの同じコードを載せておきます。

from collections import defaultdict,Counter
N,M=[int(nm) for nm in input().split()]
A=[int(a) for a in input().split()]
X=Counter(A)
AA=set(A)
B=defaultdict(int)
tmp=0
for a in sorted(AA):
    tmp+=a*X[a]
    if (a+1)%M not in AA:
        B[a%M]=tmp
        tmp=0

if tmp>0:
    AA.add(10**10)
    for i,a in enumerate(sorted(AA)):
        if i!=a:
            B[i-1]+=tmp
            break

accA=sum(A)
ans=10**20
for b in B:
    ans=min(ans,accA-B[b])

print(ans)

補足

mod 計算
X mod(Y) = Z は X を Y で割ったときの余りが Z であることを示します。
筆者も高校で出会ったとき、なかなか理解するのに苦労した記憶があります。この動画で勉強しましょう。これは令和のスタンダードですが、数学でわからないことがあれば、まずヨビノリで調べてください。
Counter
deque,defaultdict 同様、collectionsライブラリをインポートすることで利用できます。
個数管理は頻出ですので必ず使いこなしましょう。
参考 : PythonのCounterでリストの各要素の出現個数をカウント

終わり

E問題の状態で頂点を増やす発想できる人間天才過ぎます。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

【AtCoder】ABC277のA,B,C,D における Python解説

目次

はじめに

A.^{-1}

考察

前から探索

コード

補足

B.Playing Cards Validation

考察

条件1 , 条件2

条件3

計算量

コード

補足

C.Ladder Takahashi

考察

グラフにおきかえて考える

defaultdictでメモリを節約

BFS

コード

補足

D.Takahashi's Solitaire

考察

状況把握

素直に前から探索

0 と M-1 両方持っている場合

コード

補足

終わり