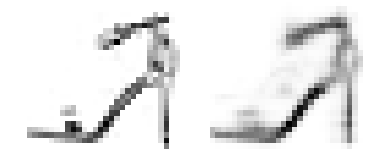はじめに
前回の記事では生成モデルと識別モデルについて説明し、分布間の距離を図るようなKLダイバージェンスについても触れました。本記事では、次元削減や異常検知に利用できるAutoencoder(オートエンコーダー)について説明していきたいと思います。さらに、Pythonで実装してみて理解を深めていきたいと思います。
↓↓↓前回の記事↓↓↓
↑↑↑↑↑↑↑↑↑↑↑
Autoencoder(自己符号化器)
Autoencoderは、入力する画像を圧縮しそれに近い画像を復元する手法です。ネットワークは入力層、中間層、隠れ層の3層になっています。入力層と出力層は元画像と同じ次元数で、中間層はその次元数よりも小さく設定します。そうすることで、少ない次元数で元の画像の特徴を抽出しているとも言えます。入力層から中間層へ向けて画像を圧縮することをエンコーダと言い、中間層から出力層へ向けて画像を復元することをデコーダと言います。Autoencoderの学習では、画像をピクセル単位で比較します。Autoencoderに限らず、画像を扱う際にはピクセル単位で学習を行うことが多いです。
数学チックな表現
上で紹介したエンコーダやデコーダについて、少し数学チックに表現していきたいと思います。トレーニングデータ$\underline{x}_1,\underline{x}_2,\dots,\underline{x}_n$が得られたとします。ただし、$\underline{x}_i\in\mathbb{R}^p,i=1,2,\dots,n$です。MNISTの手書き数字データだと1枚の画像は28$\times$28=784ピクセルの画像なので$p=784$となり、$n$はデータの個数を表しています。ここで、エンコーダ$h_{\underline{\theta}}$とデコーダ$g_{\underline{\theta}'}$を
\begin{align}
h_{\underline{\theta}}&:\mathbb{R}^p\to\mathbb{R}^r;\underline{x}\mapsto \sigma\left(W\underline{x}+\underline{b}\right),\\
g_{\underline{\theta}'}&:\mathbb{R}^r\to\mathbb{R}^p;\underline{z}\mapsto \sigma'\left(W'\underline{z}+\underline{b}'\right)\\
\end{align}
のように定義します。ただし、$r<p$であり、中間層の次元数は入力層の次元よりも小さく、圧縮しているということを表現しています。また、$W$は$(r\times p)$の重み行列、$\underline{b}$は$r$次元バイアスベクトルで、同様にして、$W'$は$(p\times r)$の重み行列、$\underline{b}'$は$p$次元バイアスベクトルを表しています。エンコーダとデコーダそれぞれの重み行列とバイアスベクトルの大きさや次元数には注意が必要です。ここで、
$\underline{\theta} = \begin{pmatrix}W^T&\underline{b}\end{pmatrix}^T,\underline{\theta}' = \begin{pmatrix}W'^T&\underline{b}'\end{pmatrix}^T$です。推定したいパラメータを$\underline{\theta},\underline{\theta}'$としてまとめています。
さらに、エンコーダとデコーダにある$\sigma:\mathbb{R}^r\to\mathbb{R}^r$や$\sigma':\mathbb{R}^p\to\mathbb{R}^p$は活性化関数です。$\sigma$や$\sigma'$によって学習の精度は変わります。エンコードの活性化関数$\sigma$ではReLUやSigmoid、デコーダの活性化関数$\sigma'$ではSigmoidやIdentityが使われるそうです。そのためデータを正規化して$[0,1]$の値を取るようにデータ加工する必要があります。ここでは、ベクトルを活性化関数で計算するというのはベクトルの各成分を活性化関数で計算していることを意味しています。
少し複雑になりましたが、エンコーダとデコーダを用いて入力層から出力層までの流れを簡単に書くと
\begin{align}
\text{入力層} &: \underline{x}\\
\text{中間層} &: h_{\underline{\theta}}\left(\underline{x}\right)=:\underline{z}\\
\text{出力層} &: g_{\underline{\theta}'}\left(\underline{z}\right)=g_{\underline{\theta}'}\left(h_{\underline{\theta}}\left(\underline{x}\right)\right)=:\underline{y}
\end{align}
のようになります。要するに中間層と出力層では前の層に対してエンコーダやデコーダを噛ませているだけですね。ちなみに、"=:"の意味は左辺を右辺で定義するという意味です。
Autoencoderの損失関数
Autoencoderの学習では、パラメータ$\underline{\theta},\underline{\theta}'$をトレーニングデータを用いて再構成誤差関数$L$(Reconstruction error function)を最小化するように構成します。これは目的関数
J_{AE}=\frac{1}{n}\sum_{i=1}^nL\left(\underline{x}_i,\underline{y}_i\right)
を最小化することに対応しています。$L$としてクロスエントロピーを使います。クロスエントロピーは
\begin{align}
\text{クロスエントロピー} &: L\left(\underline{x},\underline{y}\right)=\sum_{k=1}^{p}\left\{-x_k\log(y_k) - (1-x_k)\log(1-y_k) \right\}
\end{align}
と表されます。
前回の記事との対応を考えると、モデル分布の最適化で最後には
\mathbb{E}_{p_d}[\log p_{\underline{\theta}}(\underline{x})]
\approx
\frac{1}{n}\sum_{i=1}^{n}\log p_{\underline{\theta}}(\underline{x}_i)
を最小化すれば良いということでした。ただし、$p_{\underline{\theta}}(\underline{x})$はモデル分布、$p_d(\underline{x})$はデータ分布を表しています。$J_{AE}$の式とよく似ていると思いませんか?そう、モデル分布として二項分布を仮定すれば、上の話と一致します。
具体的にどうやって最適化するのかということには触れません。実際にPythonで見ていきましょう。
AutoencoderのPython実装
それでは、AutoencoderをPythonで実装していきますが、特に「異常検知」に着目して実装を行います。すなわち、AutoEncoderを用いて異常検知を行います。紹介するコードはColaboratoryで実行できることを確認しています。ローカルで実行しようと思いましたが8Gメモリではダメでした。
本記事で使用したデータはFashion-MNISTデータです。このデータは、28$\times$28ピクセルの10種類の服や靴、バッグなどのファッションの白黒の画像データです。トレーニング用には60000個、テストデータ用には10000個のデータがあります。こちらからcsvファイルを入手しました。ラベルは10種類ありましたが、これをさらに大きく分けると、服、ズボン、靴、カバンになります。ここは私の主観で分けていますのでご注意ください。これについては、「データの前処理」という項目で紹介します。この大別から、靴を正常データ、服を異常データとしてAutoencoderで異常検知を行います。
前置きが長くなりましたが、データの読み込みから学習、結果の可視化まで行っていきたいと思います。
準備
データの読み込みや学習の前に準備を行います。
ライブラリのインポート
今回使ったライブラリをインポートします。
# よく使うライブラリ
import numpy as np
import pandas as pd
# torchライブラリ
import torch
import torchvision
from torch.utils.data import DataLoader
# 学習に関するライブラリ
import torch.nn as nn
import torch.optim as optimizers
from tqdm.notebook import tqdm
# 図の描画に関するライブラリ
import seaborn as sns
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
乱数の固定
再現性を持たせるために乱数を固定します。
np.random.seed(777)
torch.manual_seed(777)
演算を行うデバイス
演算を行うデバイスの設定のための準備を行います。ColaboratoryでGPUを使うには、こちらの「Google Colab環境でGPUを使うには」という項目を参考にしてください。
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)
を実行してみて、
cuda
が出力されれば、GPUを使える状態になっています。
データの準備・前処理・可視化
データを読み込み、前処理もしていきましょう。前処理といってもほとんど何もしていません。ラベルごとに分けたり、Tensor型にしているだけです。Tensor型とは?と思った人はこちらが参考になるかもしれません。
データの読み込み
csvファイルのあるフォルダまでのパスをXXXXXに入れてください。ここは人によって違いが出てきます。私は、Colaboratoryでマウントしてそのパスを入れました。マウントすることによって、自分のGoogle Driveにあるデータを読み込むことができます。こちらの記事が参考になるかもしれません。
train_data = pd.read_csv("XXXXX/fashion_mnist_train.csv")
test_data = pd.read_csv("XXXXX/fashion_mnist_test.csv")
データの前処理
Fashion-MNISTデータには10種類のラベルがあります。それぞれのラベルについては次のようになっています。
- 0:"T-Shirt"
- 1:"Trouser"
- 2:"Pullover"
- 3:"Dress"
- 4:"Coat"
- 5:"Sandal"
- 6:"Shirt"
- 7:"Sneaker"
- 8:"Bag"
- 9:"Ankle Boot"
以上のように、ラベル0,2,3,4,6は服、1はズボン、5,7,9は靴、8はカバンというように分けられます。先ほども記しましたが、靴を正常データ、服を異常データとして異常検知をAutoencoderで行います。それでは、ラベルごとにトレーニングデータを
train_data0 = train_data[train_data["ID"] == 0].iloc[:,1:]
train_data1 = train_data[train_data["ID"] == 1].iloc[:,1:]
train_data2 = train_data[train_data["ID"] == 2].iloc[:,1:]
train_data3 = train_data[train_data["ID"] == 3].iloc[:,1:]
train_data4 = train_data[train_data["ID"] == 4].iloc[:,1:]
train_data5 = train_data[train_data["ID"] == 5].iloc[:,1:]
train_data6 = train_data[train_data["ID"] == 6].iloc[:,1:]
train_data7 = train_data[train_data["ID"] == 7].iloc[:,1:]
train_data8 = train_data[train_data["ID"] == 8].iloc[:,1:]
train_data9 = train_data[train_data["ID"] == 9].iloc[:,1:]
のように実行して分割します。0列目の列名は"ID"でありラベルの情報が入っているため、.iloc[:,1:]として、各画像の各ピクセルの値だけを取り出しています。続いて、靴系をshoes、服系をclothesとしてデータをconcatでまとめています。これよりシンプルなやり方があれば教えていただきたいです。
shoes = pd.concat([train_data5, train_data7], axis = 0)
shoes = pd.concat([shoes, train_data9], axis = 0)
clothes = pd.concat([train_data0, train_data2], axis = 0)
clothes = pd.concat([clothes, train_data3], axis = 0)
clothes = pd.concat([clothes, train_data4], axis = 0)
clothes = pd.concat([clothes, train_data6], axis = 0)
データの可視化
どんなデータなのかを可視化しましょう。特に靴と服のデータを見てみます。靴データからランダムに25個選んでそれを描画します。白黒画像は0に近いと黒、255に近いと白を表します。すなわち、値が大きいところが白色となり、画像が浮き上がるため直感とは逆になるかと思います。ここでは、255から各ピクセルの値を引くことで白黒反転します。これについては、コードの2行目に記載があります。
pixel_size = 28
learning_data = (255 - shoes).copy()
x_img = learning_data.to_numpy().reshape([learning_data.shape[0], pixel_size, pixel_size])
fig = plt.figure(figsize = (8,6))
fig.subplots_adjust(wspace = 0.1, hspace = 0.1)
for i in range(0,25):
idx = random.randint(0, len(learning_data))
axes = fig.add_subplot(5, 5, i%25+1)
axes.imshow(x_img[idx,:], cmap='gray')
axes.axis("off")
実行して得られる図形は次のようになります。色々な靴がありますね。
続いて、服の描画ですが、コードの2行目のshoesをclothesにすれば良いです。これを実行すると次のようになります。

Tensor型への変換
Tensor型でデータを変換し、GPUを使用して演算等を可能にします。さらに、本記事では学習をミニバッチ学習で行うため、データをDataloaderに渡します。最初に255.0で割っているのは、0から1の値をとるように正規化しています。これは、「学習」の項目でも触れますが、デコーダの活性化関数にSigmoid関数を用います。Sigmoid関数は0から1の出力であるため、入力値と出力値の範囲を同じにするために正規化を行っています。同じにする理由は入力と同じになるように学習をするというAutoencoderの特徴のためです。また、ミニバッチのバッチサイズは64として行ってみます。バッチサイズは、メモリとの関係で2のべき乗とすると良いそうです。
x_train = learning_data.astype(np.float32) / 255.0
x_train = x_train.to_numpy().reshape((len(x_train), np.prod(x_train.shape[1:])))
train_tor = torch.tensor(x_train).float()
batch_size = 64
train_loader = DataLoader(train_tor, batch_size = batch_size, shuffle = True)
学習
データの準備、前処理をしたので、次に学習を行っていきましょう。まずは、Autoencoderのネットワークの定義をします。
ネットワークの定義
class Autoencoder(nn.Module):
def __init__(self, device = "cpu"):
super().__init__()
self.device = device
self.l1 = nn.Linear(784, 200)
self.l2 = nn.Linear(200,784)
def forward(self, x):
#エンコーダ
h1 = self.l1(x)
#エンコーダの活性化関数はRelu関数
h2 = torch.relu(h1)
#デコーダ
h3 = self.l2(h2)
#デコーダの活性化関数はシグモイド関数
y = torch.sigmoid(h3)
return y
forward関数の中に色々と関数があります。これと、上で記載している「数学チックな表現」という項目との対応を見ていきましょう。まず、$p=784$で$r=200$ですね。そして、h1は$\mathbb{R}^{784}$から$\mathbb{R}^{100}$への線形変換$W\underline{x}+\underline{b}$を表しています。そして、h2のRelu関数は$\sigma$に対応します。同じように、h3は$\mathbb{R}^{100}$から$\mathbb{R}^{784}$への線形変換$W'\underline{z}+\underline{b}'$を表しており、yのSigmoid関数は$\sigma'$に対応しています。
少しややこしいかもしれませんがコードに現れる関数がどの関数に対応しているかの把握は重要だと思っていますので、このように対応の説明しました。
モデル、損失関数、最適化関数の設定
学習のモデル、損失関数、最適化関数の設定を行います。モデルは先ほどの「ネットワークの定義」の項目で行ったものです。続いて、損失関数はクロスエントロピーを用います。他にも様々な損失関数がありますので、こちらのLoss Functionsという項目をご参照ください。そして、最適化の計算にはAdamを使っています。
# モデルの設定
model = Autoencoder(device = device).to(device)
# 損失関数の設定
criterion = nn.BCELoss()
# 最適化関数の設定
optimizer = optimizers.Adam(model.parameters())
学習の実行
いよいよ学習の実行です。エポック数を30として行います。また、tqdm()関数を使って、学習の進み具合を可視化しています。最後には損失関数の値をプロットしています。
epochs = 30
# エポックのループ
loss_val = []
for epoch in tqdm(range(epochs)):
train_loss = 0.
#バッチサイズのループ
for x in train_loader:
x = x.to(device)
# 訓練モードへの切替
model.train()
# 順伝播計算
preds = model(x)
# 入力画像xと復元画像predsの誤差計算
loss = criterion(preds, x)
# 勾配の初期化
optimizer.zero_grad()
# 誤差の勾配計算
loss.backward()
# パラメータの更新
optimizer.step()
# 訓練誤差の更新
train_loss += loss.item()
train_loss /=len(train_loader)
loss_val.append(train_loss)
plt.plot(range(1,epochs+1), loss_val)
plt.show()
エポックごとに損失関数の値が減少していることがわかります。良い感じです。
学習結果
試しに一つだけ画像を復元してみましょう。
# data_loaderからデータの取り出し
x = next(iter(train_loader))
x = x.to(device)
# 評価モードへの切り替え
model.eval()
# 復元画像
idx = 0
x_rec = model(x)
# 入力画像、復元画像の表示
for i, image in enumerate([x[idx], x_rec[idx]]):
image = image.view(28, 28).detach().cpu().numpy()
plt.subplot(1, 2, i + 1)
plt.imshow(image, cmap = "gray")
plt.axis("off")
plt.show()
左側は元の画像、右側が復元した画像になります。ぼやけてはいますがちゃんと靴の画像を復元できていそうですね。
異常検知
服のデータを入力とします。これをTensor型に変換します。試しに一つ復元してみましょう。
anomaly_data = clothes.copy()
x_test = (255.0-anomaly_data).astype(np.float32) / 255.0
x_test = x_test.to_numpy().reshape((len(x_test), np.prod(x_test.shape[1:])))
test_tor = torch.tensor(x_test).float()
test_loader = DataLoader(test_tor, batch_size=batch_size, shuffle=False)
# data_loaderからデータの取り出し
x = next(iter(test_loader))
x = x.to(device)
# 評価モードへの切り替え
model.eval()
idx = 0
x_rec = model(x)
# 入力画像、復元画像の表示
for i, image in enumerate([x[idx], x_rec[idx]]):
image = image.view(28, 28).detach().cpu().numpy()
plt.subplot(1, 2, i + 1)
plt.imshow(image, cmap = "binary_r")
plt.axis("off")
plt.show()
靴を学習しているので服はこのようにぼやけてしまっていますね。なんとなくブーツにも見えなくはないですが、服ではないことは確かです。
正常データと異常データの誤差に着目
次に正常データと異常データの誤差に着目してみます。ここでいう誤差とは、元の画像と復元した画像の各ピクセル毎の二乗誤差の和のことです。これを各画像ごとに計算します。本記事ではバッチサイズの分だけ箱ひげ図を用いて見てみることにします。
# 正常データ(shoes)の誤差
x = next(iter(train_loader))
x = x.to(device)
x_rec = model(x)
error_of_normal = []
for i in range(batch_size):
error_of_normal.append(sum(((x[i]-x_rec[i])**2).tolist()))
# 異常データ(clothes)の誤差
x = next(iter(test_loader))
x = x.to(device)
x_rec = model(x)
error_of_anomaly = []
for i in range(batch_size):
error_of_anomaly.append(sum(((x[i]-x_rec[i])**2).tolist()))
# それぞれの箱ひげ図を描画
fig, ax = plt.subplots()
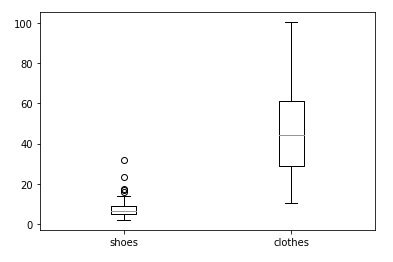
bp = ax.boxplot((error_of_normal,error_of_anomaly))
ax.set_xticklabels(['shoes', 'clothes'])
plt.show()
左側が正常データ、右側が異常データの誤差の箱ひげ図です。全体的には異常データの誤差が大きくなっていることがわかります。一方で、正常データに誤差が大きいもの、異常データに誤差が小さいものがあり、完璧に異常検知ができるとは言えないでしょう。層の数を変えたり、活性化関数の選択やエポック数など調整することでまだ学習精度が向上できるかもしれません。とにもかくにも、Autoencoderを実装できなんとなく異常検知に使えそうで、本記事ではあまり触れてはいないですが特徴抽出にも使えそうだなと思いました。
まとめ
Autoencoderの簡単な説明から実装までを行ってきました。異常データの服を復元したとき、なんとなく靴っぽくなっている点が面白かったです。Autoencoderの派生系は他にもたくさんあるそうなので今後の課題です。ここまで読んでくださりありがとうございました。
参考文献
毛利拓也, 大郷友海, 嶋田宏樹, 大政孝充, むぎたろう, 寅蔵, もちまる(2021). GANディープラーニング実装ハンドブック. 秀和システム