はじめに
最近、技術の向上により非常に精度の高い画像が生成されていることを知り、その技術を支えている「画像生成」に興味を持ちました。人物画像や背景画像を生成したとすると本物と見間違うほどの精度だったりします。また、画像生成の用途として、人物の画像生成では肖像権にひっかからないため有用です。何しろ画像なので視覚的にもわかりやすいです。画像データの水増しにも使うこともできます。画像生成では、「生成モデル」を通して画像が生成されます。生成モデルには、VAE(Variational Autoencoder:変分オートエンコーダー)やGAN(Generative Adversarial Networks:敵対的生成ネットワーク)などがあります。生成モデルは機械学習における教師なし学習にあたります。一方、教師あり学習には分類問題があり、「識別モデル」を通して画像分類などを行います。本投稿では識別モデルと生成モデルについて説明していきたいと思います。
識別モデル
教師あり学習における分類問題のタスクは、正解ラベルと特徴量のペアのデータ
(y_1,\underline{x}_1),(y_2,\underline{x}_2),\dots,(y_n,\underline{x}_n)
に対して、識別モデル$h_{\underline{\theta}}(\underline{x})$の中にあるパラメータ$\underline{\theta}$を最適化することです。それぞれ
- $y_i,~i=1,2,\dots,n$ : 目的変数、被説明変数、正解ラベル。
- $\underline{x}_i,~i=1,2,\dots,n$ : 説明変数、特徴量。$\underline{x}$は$p$次元ベクトル、すなわち$\underline{x}\in\mathbb{R}^p$としときます。下線付きはベクトル
\underline{x}=\begin{pmatrix}x_1&x_2&\dots&x_p\end{pmatrix}^T
を表しています。右上の$T$は転置記号で、$\underline{x}$は行列でいうと$p\times1$行列となっています。
- $\underline{\theta}$ : パラメータベクトル。パラメータの与え方によってモデルの精度が異なりますので、そのパラメータをどう決めるかが鍵となっています。識別モデルとして線形モデル$h_{\underline{\theta}}(\underline{x})=a+\underline{b}^T\underline{x}$を考えると、$\underline{\theta}$は$a$と$\underline{b}$をまとめた$(p+1)$次元のベクトル
\underline{\theta}=\begin{pmatrix}a&\underline{b}\end{pmatrix}^T\in\mathbb{R}^{p+1}
を表しています。
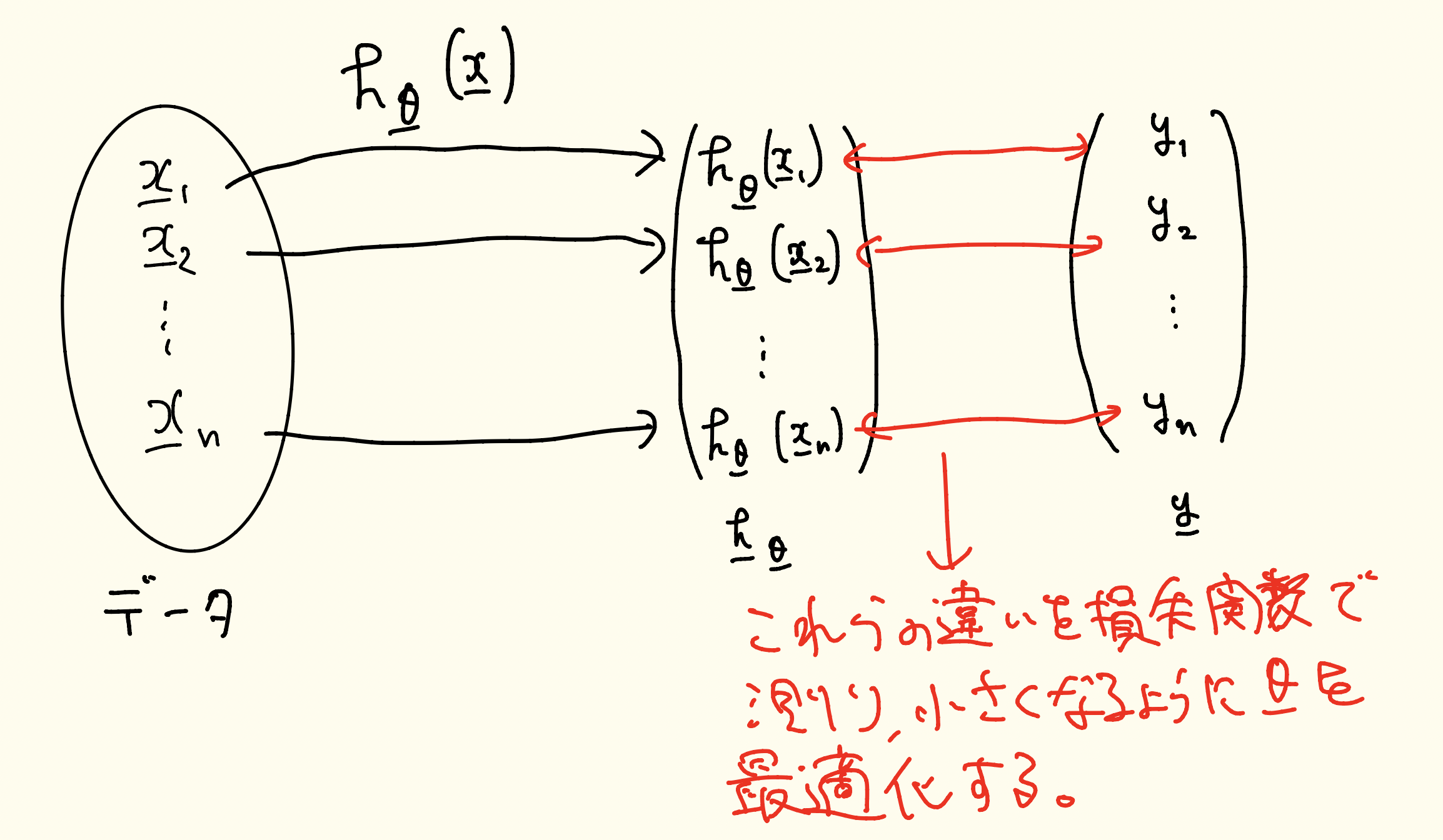
識別モデルには「学習」と「予測」の2つのプロセスがあります。学習プロセスでは、データ$\underline{x}_1,\underline{x}_2,\dots,\underline{x}_n$をそれぞれ識別モデルに入れ、そこから得られた分類ベクトル$\underline{h} _{\underline{\theta}}$と正解ラベルのベクトル$\underline{y}$の誤差を損失関数で計算し、損失関数を最小化するようにパラメータ$\underline{\theta}$を最適化します。ここで、
\underline{h}_{\underline{\theta}}=\begin{pmatrix}h_{\underline{\theta}}(\underline{x}_1)&h_{\underline{\theta}}(\underline{x}_2)&\dots&h_{\underline{\theta}}(\underline{x}_n)\end{pmatrix}^T, \underline{y}=\begin{pmatrix}y_1&y_2&\dots&y_n\end{pmatrix}^T
を表しています。図で簡単に表すと次の図ようになります。
続いて、予測プロセスでは、未知のデータ$\underline{x}'$を学習プロセスで最適化されたパラメータ$\hat{\underline{\theta}}$を持つ識別モデルに入れて、$h_{\hat{\underline{\theta}}}(\underline{x}')$で予測します。分類問題ではロジスティック回帰などが有名です。ロジスティック回帰では、データがあるクラス(ここでは簡単のためAクラスとBクラスにします)に属する確率を推定し、ある閾値を定めその閾値以上だとAクラス、その閾値未満だとBクラスに分類しています。
以上より、識別モデルを定式化すると、「データ$\underline{x}$が与えられたときの正解ラベル$y$の条件付き確率$p(y|\underline{x})$を出力するモデル」になります。
生成モデル
画像分類における問題では、画像データを畳み込みやプーリングなどで特徴を抽出し縮小します。その後、全結合と呼ばれる操作でベクトルに変換し、識別モデルを通して分類ベクトルに変換します。一方生成モデルでは、この逆のような操作をイメージすればよく、あるベクトルから生成モデルを通して画像を生成します。
生成モデルは、教師なし学習に含まれており正解ラベルがありません。そのため、データ$\underline{x}$と確率分布を使って生成モデルを構築していきます。
生成モデルを定式化すると、「確率変数からデータ$\underline{x}$を出力する確率$p(\underline{x})$を出力するモデル」になります。正解ラベルが与えられたときには、条件付き確率$p(\underline{x}|y)$の出力も可能になります。すなわち、先程の例だとAクラスに属するデータを出力することができるようになります。
また、生成モデルが出力する確率$p(\underline{x})$をモデル分布と呼びます。
データ$\underline{x}$がある確率分布$p_d(\underline{x})$に従うと仮定して、$p_d(\underline{x})$に近くなるようにモデル分布$p(\underline{x})$を構築していきます。よって、生成モデルでも識別モデルと同じように最適化が鍵となっています。次にその最適化について紹介していきます。
生成モデルの最適化
生成モデルの最適化のポイントは「モデル分布が確率分布$p_{\underline{\theta}}(\underline{x})$に従うと仮定する」ことです。モデル分布がパラメータ$\underline{\theta}$を持つとすることで、$\underline{\theta}$を最適化することでデータ分布$p_d(\underline{x})$に近づけることができます。生成モデルの学習プロセスは最尤推定(最も尤もらしいパラメータを推定する方法)を通して$\underline{\theta}$を推定します。推論プロセスでは、最適化されたモデル分布を用いることでデータ$\underline{x}$を生成できるようになります。
さて、モデル分布$p(\underline{x})$がデータ分布$p_d(\underline{x})$に近くなるようにパラメータ$\underline{\theta}$を推定しますと言いましたが、「確率分布が近い」とはどのように測ればよいのでしょうか?ここで、登場するのが「KLダイバージェンス(Kallback-Leibler divergence)」です。
KLダイバージェンスとJSダイバージェンス
KLダイバージェンス
D_{KL}\left({\color{red}p}~\big|\big|~{\color{blue}q}\right)=\int {\color{red}p}(\underline{x})\log\frac{{\color{red}p}(\underline{x})}{{\color{blue}q}(\underline{x})}d\underline{x}
は確率分布${\color{red}p}$と確率分布${\color{blue}q}$の距離を測ります。積分の範囲は$\underline{x}$の取りうる値すべての領域です。2つの分布が近いと0に近づき、遠いと大きな値となります。また、0以上に値をとり、2つの確率分布が一致すると0となり最小となります。通常の距離には対称性も性質として挙げられますが、KLダイバージェンスは対称性も持ちません。つまり、
D_{KL}\left({\color{red}p}~\big|\big|~{\color{blue}q}\right)\neq D_{KL}\left({\color{blue}q}~\big|\big|~{\color{red}p}\right)
ということです。KLダイバージェンスを組みあわせることで対称性を持つようにしたJSダイバージェンス
D_{JS}\left({\color{red}p}~\big|\big|~{\color{blue}q}\right)
=\frac{1}{2}D_{KL}\left({\color{red}p}~\Big|\Big|~\frac{{\color{red}p}+{\color{blue}q}}
{2}\right)
+\frac{1}{2}D_{KL}\left({\color{blue}q}~\Big|\Big|~\frac{{\color{red}p}+{\color{blue}q}}
{2}\right)
というものもあります。KLダイバージェンスと異なりJSダイバージェンスは対称性
D_{JS}\left({\color{red}p}~\big|\big|~{\color{blue}q}\right)=D_{JS}\left({\color{blue}q}~\big|\big|~{\color{red}p}\right)
を持っています。JSダイバージェンスはGANで使われたりするそうです。
モデル分布の最適化
モデル分布を最適化するには、モデル分布$p_{\underline{\theta}}(\underline{x})$とデータ分布$p_d(\underline{x})$のKLダイバージェンスを測りそれが小さくなるようにパラメータ$\underline{\theta}$を調整すればよいことになります。これら2つのKLダイバージェンスを書き換えていくと
\begin{align}
D_{KL}\left(p_d~\big|\big|~p_{\underline{\theta}}\right)
& =
\int p_d(\underline{x})\log\frac{p_d(\underline{x})}{p_{\underline{\theta}}(\underline{x})}d\underline{x}\\
& =
\int p_d(\underline{x})\log p_d(\underline{x})d\underline{x}
-
\int p_d(\underline{x})\log p_{\underline{\theta}}(\underline{x})d\underline{x}\\
& =
\mathbb{E}_{p_d}[\log p_d(\underline{x})]
-
\mathbb{E}_{p_d}[\log p_{\underline{\theta}}(\underline{x})]
\end{align}
というようになります。ただし、$\mathbb{E}_{p_d}[\cdot]$はデータ分布$p_d$上の期待値を表しています。第一項目はパラメータ$\underline{\theta}$に依存せず、$\underline{\theta}$の最適化には関係のない項になっています。第二項に$\underline{\theta}$が含まれているので、この第二項が$\underline{\theta}$の最適化に関係があります。よって、KLダイバージェンスを最小化するには第二項目を最大化すればよいことになります。しかし、データ分布$p_d$は具体的にはわからないので第二項目の期待値は直接計算できません。この期待値を$n$個の平均で近似することで計算を行います。すなわち、
\mathbb{E}_{p_d}[\log p_{\underline{\theta}}(\underline{x})]
\approx
\frac{1}{n}\sum_{i=1}^{n}\log p_{\underline{\theta}}(\underline{x}_i)
というように近似します。これはモデル分布の対数尤度を表しています。この対数尤度を最大化する手法は最尤法として知られており、様々な場面で登場します。
まとめ
識別モデルと生成モデルを紹介し、生成モデルを最適化するために最尤法が用いられていることを学びました。その過程で分布間の距離を測るKLダイバージェンスやJSダイバージェンスについても紹介しました。KLダイバージェンスはVAEで用いられるのでしっかりと覚えておきたいです。
参考文献
毛利拓也, 大郷友海, 嶋田宏樹, 大政孝充, むぎたろう, 寅蔵, もちまる(2021). GANディープラーニング実装ハンドブック. 秀和システム