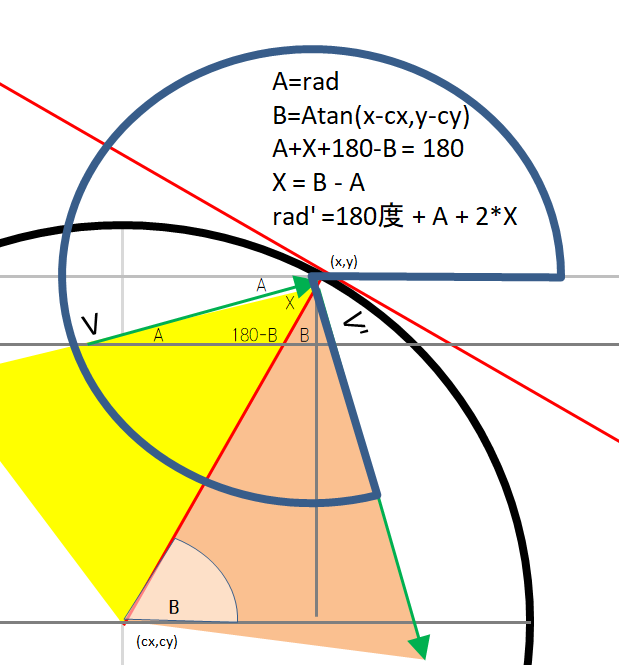
円の中を反射する点をgnuplotで描画したい!
前回間違えて記事に質問を投稿してしまったので、質問欄にリベンジ投稿します!ぜひ知識を貸してください!!
解決したいこと
大学の授業でC言語を勉強しています。
授業で正方形の中を反射して動く点のコードを作りました。そこで、追加の課題として円の中を反射する点を描画するというものが出題されました。
自分で作っては見たのですが、うまくいかなかったので教えていただきたいです。
参考に、正方形の中を反射するコードは、以下に貼っておきます。(20回反射したら終了するようになっています。)
//ball.c
#include <stdio.h>
#include <unistd.h>
#include <math.h>
int main(void){
FILE *gp,*fp;
int counter = 0;
int counter_max = 20;
double x,y, vx,vy;
// set boundary condition//
double xmin = 0.0;
double ymin = 0.0;
double xmax = 2.0;
double ymax = 2.0;
fp = fopen("trajectory.dat","w"); // 軌跡を保存
gp = popen("gnuplot", "w"); //
fprintf(gp,"set terminal gif animate delay 2 loop 0; set output 'ball.gif'\n"); // 描画した結果をgifに保存
fprintf(gp, "set border 0\n"); // 枠線を消す
fprintf(gp, "set object 1 rect from first %f, first %f to first %f, first %f back fc rgb 'white' fs solid\n", xmin,ymin,xmax,ymax);
// boxの背景を白抜きにする
fprintf(gp, "set xrange [%f:%f]\n",xmin-0.5,xmax+0.5);
fprintf(gp, "set yrange [%f:%f]\n",ymin-0.5,ymax+0.5);
fprintf(gp, "set size square\n");
fprintf(gp, "unset tics\n");
// set initial condition //
x = 0.2;
y = 0.2;
vx = 0.02;
vy = sqrt(2.0)*0.01;
while (counter < counter_max){
x = x + vx;
y = y + vy;
if(x>=xmax) {
x=2.0*xmax-x;
vx=-vx;
counter += 1;
}
if(x<=xmin) {
x=-x;
vx=-vx;
counter += 1;
}
if(y>=ymax) {
y=2.0*ymax-y;
vy=-vy;
counter += 1;
}
if(y<=ymin) {
y=-y;
vy=-vy;
counter += 1;
}
fprintf(fp,"%f %f\n", x,y);
fprintf(gp,"set title '%d-th bounces'\n", counter);
fprintf(gp,"plot '-'w p pt 7 ps 7 lc 3 tit ''\n");
fprintf(gp,"%f %f\n",x,y);
fprintf(gp,"e\n");
fflush(gp);
usleep(5000);
}
return 0;
}
0 likes