Physics-Informed Neural Networks (PINNs)による減衰振動の運動方程式の解法とその図解

はじめに

　近年、物理法則を加味した機械学習が多く登場してきてます。
　PINNsの概念は2017年にRaissiら【文献 1】、【文献 2】によって最初の報告があり、2019年に非線形偏微分方程式の解法【文献 3】に適用され、注目を集めることとなりました。
　すでにいくつかのコードや考え方も記されているので、

Physics-Informed Neural Networks (PINNs)を減衰振動の運動方程式に適用してみた！
PINNs(Physics Informed Neural Networks)に挑戦してみた

　ここでは、バネによる減衰振動の解法について、DNNとPINNsの違いについて、その流れを図解したいと思います。

図解

　DNNおよびPINNsも基本的な流れは同じです。
　与えられたデータに対して、最適な層を構成して損失を計算します。
　損失が最小になるように、ネットワーク中の重みやバイアスを計算するため偏微分してこれらを更新します。
　新たな重みやバイアスを与えて、再度、損失が最小になるように計算を進めています。

データ駆動型のDNNとPINNsの違い

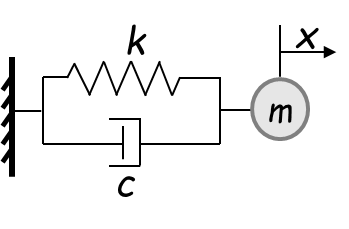
　バネの減衰方程式は、$t$と$x$の関数で成り立っています。

 m \frac{d^2x}{dt^2} + c \frac{dx}{dt} + kx = 0　

　DNNでは、時間$t$を与えたときに、予測値$x$を算出できるニューラルネットワークを構築し、勾配降下法を用いて予測誤差が最小になるように重みを更新します。
　一方、Physics-Informed Neural Networks（PINNs）は、得られたデータ解と運動方程式から誤差を求め、データからの誤差と物理法則による誤差の総和が最小になるように勾配降下法で重み等を更新し、誤差を縮小する手法です。図中のλが物理法則による誤差をどこまで含めるかということを示しています。単純な計算では発散しないのですが、複雑な場合この値を大きくしすぎると発散し易くなります。

　下記のサンプルデータを動かせば、結果図のようなgifが作成できます。

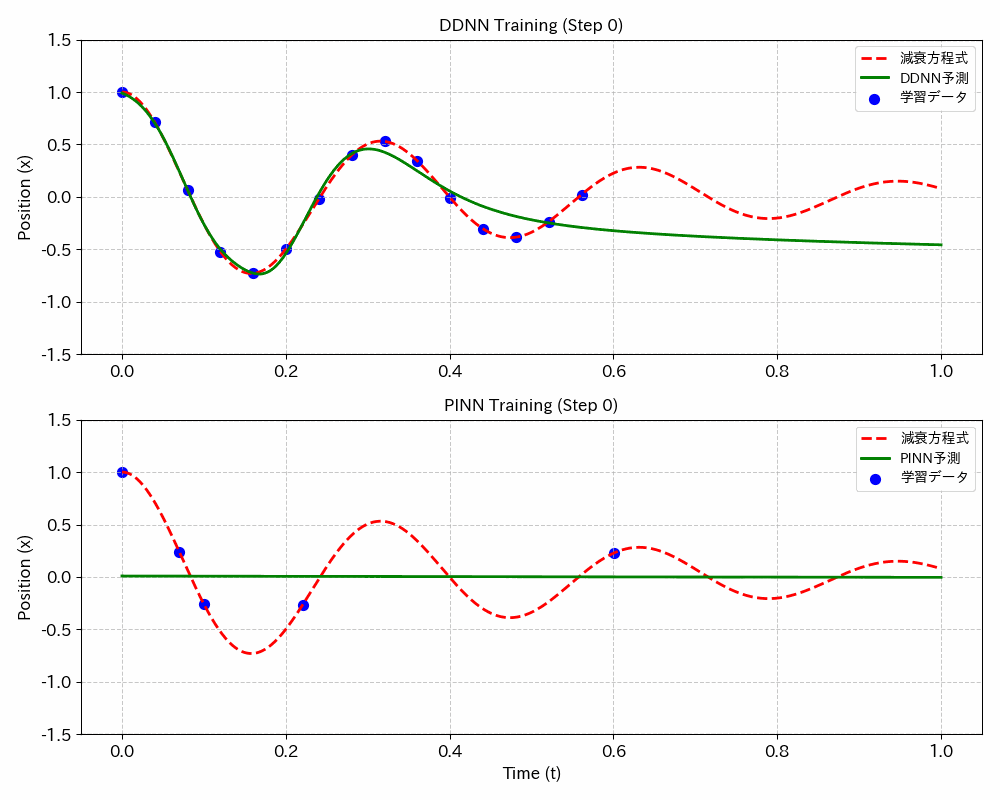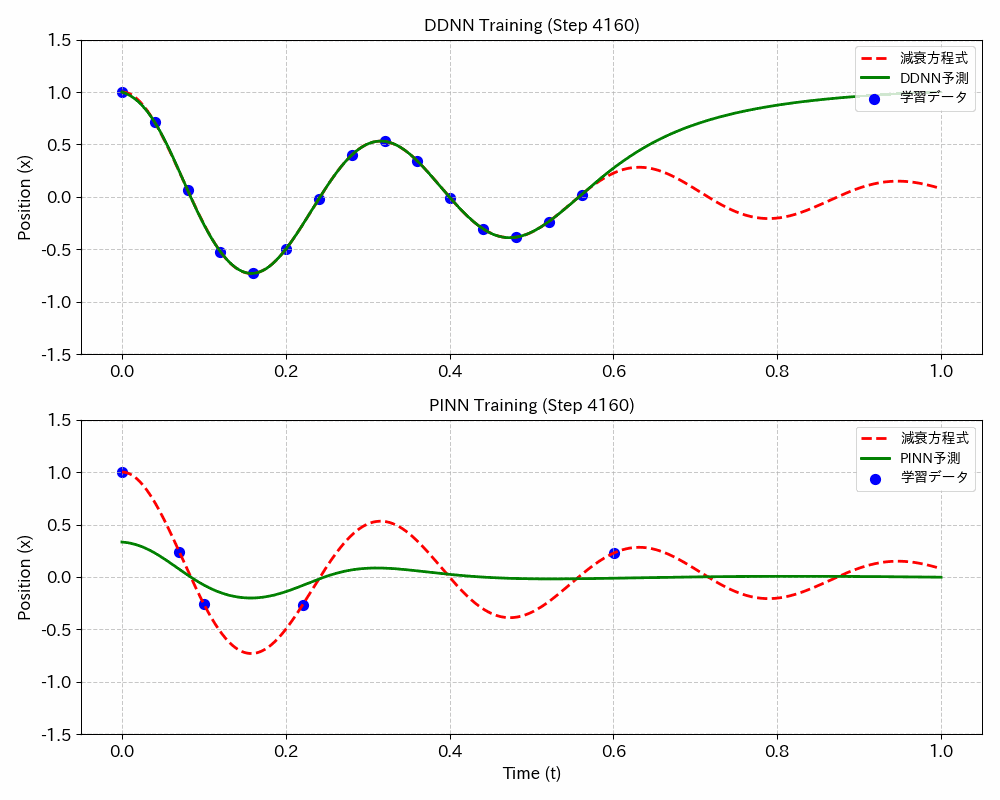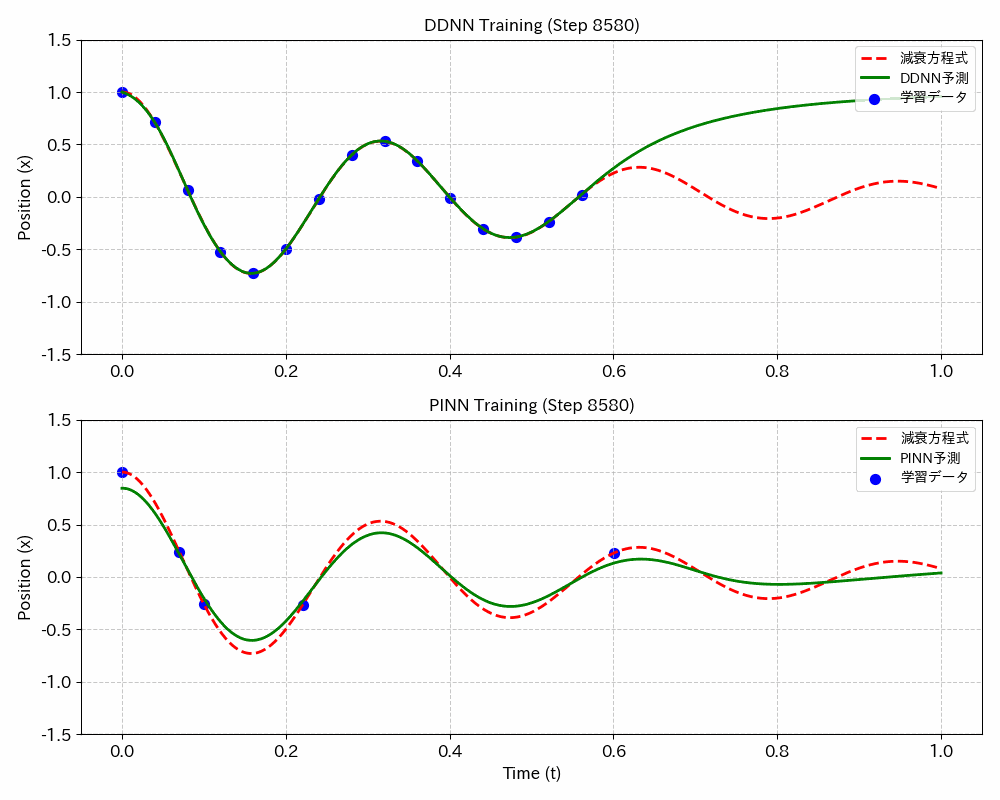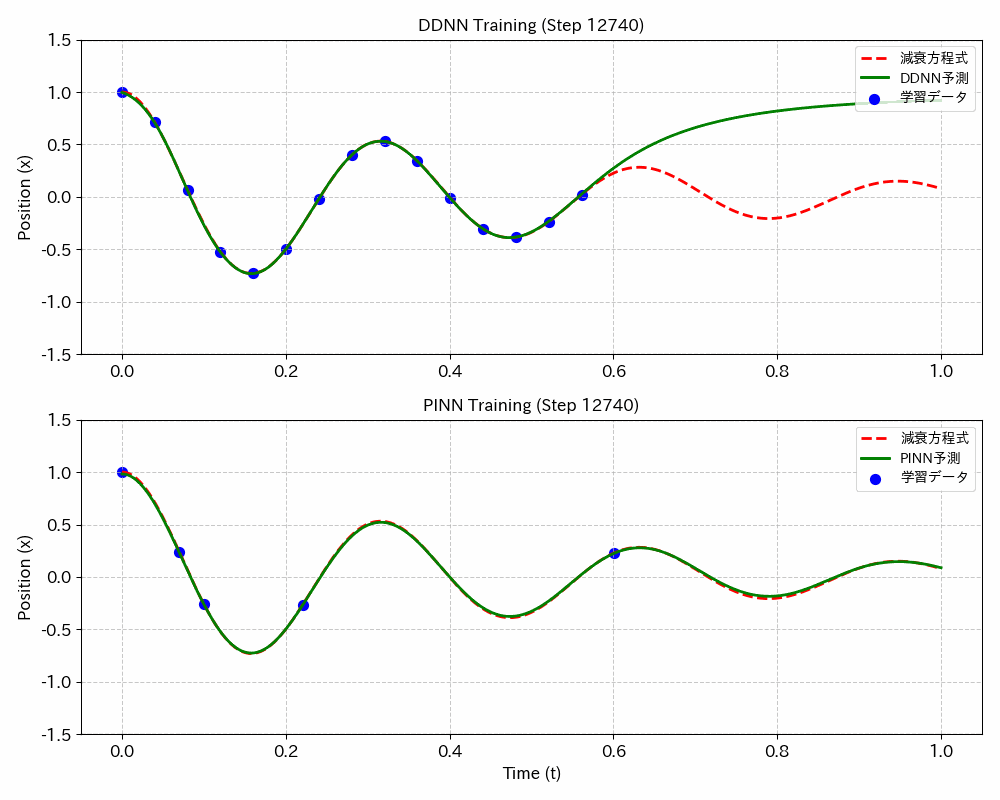
結果図

　DDNN（データドリブンニューラルネットワーク；今のところ一般的な呼び名では無いようです、念のため）に比べてPINNsは、学習データが少なくて最適な学習ができるうえ、学習していないデータ範囲でも最適な値が得られます。

データ生成

# data_generator.pyとして保存

import numpy as np
import tensorflow as tf

def FDM(init_x, init_v, init_t, gamma, omega, dt, T):
    x, v, t = init_x, init_v, init_t
    g, w0 = gamma, omega
    num_iter = int(T/dt)

    alpha = np.arctan(-1*g/np.sqrt(w0**2 - g**2))
    a = np.sqrt(w0**2 * x**2 / (w0**2 - g**2))

    t_array, x_array, v_array = [], [], []
    x_analytical_array, diff_array = [], []

    for i in range(num_iter):
        fx = v
        fv = -1*w0**2 * x - 2*g * v
        x = x + dt * fx
        v = v + dt * fv
        t = t + dt
        x_a = a * np.exp(-1*g * t) * np.cos(np.sqrt(w0**2 - g**2) * t + alpha)
        diff = x_a - x

        t_array.append(t)
        x_array.append(x)
        x_analytical_array.append(x_a)
        v_array.append(v)
        diff_array.append(diff)

    return t_array, x_array, v_array, x_analytical_array, diff_array

def analytical_solution(g, w0, t):
    assert g <= w0
    w = np.sqrt(w0**2-g**2)
    phi = np.arctan(-g/w)
    A = 1/(2*np.cos(phi))
    cos = tf.math.cos(phi+w*t)
    sin = tf.math.sin(phi+w*t)
    exp = tf.math.exp(-g*t)
    x = exp*2*A*cos
    return x

def generate_training_data(g=2.0, w0=20.0, n_points=500):
    # Generate time points
    t = tf.linspace(0, 1, n_points)
    t = tf.reshape(t, [-1, 1])
    
    # Generate analytical solution
    x = analytical_solution(g, w0, t)
    x = tf.reshape(x, [-1, 1])
    
    # Create data points for DDNN (evenly spaced)
    ddnn_indices = [i for i in range(0, 300, 20)]
    t_data_ddnn = tf.gather(t, ddnn_indices)
    x_data_ddnn = tf.gather(x, ddnn_indices)
    
    # Create data points for PINN (random points)
    pinn_indices = [0, 35, 50, 110, 300]
    t_data_pinn = tf.gather(t, pinn_indices)
    x_data_pinn = tf.gather(x, pinn_indices)
    
    # Generate PINN collocation points
    t_pinn = tf.linspace(0, 1, 30)
    t_pinn = tf.reshape(t_pinn, [-1, 1])
    
    return {
        't': t,
        'x': x,
        't_data_ddnn': t_data_ddnn,
        'x_data_ddnn': x_data_ddnn,
        't_data_pinn': t_data_pinn,
        'x_data_pinn': x_data_pinn,
        't_pinn': t_pinn,
        'c': 2*g,
        'k': w0**2
    }

トレーニング

# training.pyとして保存


import tensorflow as tf

def MLP(n_input, n_output, n_neuron, n_layer, act_fn='tanh'):
    '''関数
    Args:
        n_input: 入力層のユニット数
        n_output: 出力層のユニット数
        n_neuron: 隠れ層のユニット数
        n_layer: 隠れ層の層数
        act_fn: 活性化関数
    Returns:
        model: MLPモデル
    '''
    tf.random.set_seed(1234)
    model = tf.keras.Sequential([
        tf.keras.layers.Dense(
            units=n_neuron,
            activation=act_fn,
            kernel_initializer=tf.keras.initializers.GlorotNormal(),
            input_shape=(n_input,),
            name='H1')
    ])
    
    for i in range(n_layer-1):
        model.add(
            tf.keras.layers.Dense(
                units=n_neuron,
                activation=act_fn,
                kernel_initializer=tf.keras.initializers.GlorotNormal(),
                name='H{}'.format(str(i+2))
            ))
    
    model.add(
        tf.keras.layers.Dense(
            units=n_output,
            name='output'
        ))
    return model

class EarlyStopping:
    def __init__(self, patience=10, verbose=0):
        self.epoch = 0
        self.pre_loss = float('inf')
        self.patience = patience
        self.verbose = verbose

    def __call__(self, current_loss):
        if self.pre_loss < current_loss:
            self.epoch += 1
            if self.epoch > self.patience:
                if self.verbose:
                    print('early stopping')
                return True
        else:
            self.epoch = 0
            self.pre_loss = current_loss
        return False

# データ駆動型ニューラルネットワーク
class DataDrivenNNs:
    def __init__(self, n_input, n_output, n_neuron, n_layer, epochs, act_fn='tanh'):
        """
        データ駆動型ニューラルネットワークの初期化
        
        Parameters:
        n_input: 入力層のニューロン数
        n_output: 出力層のニューロン数
        n_neuron: 隠れ層の1層あたりのニューロン数
        n_layer: 隠れ層の層数
        epochs: 学習エポック数
        act_fn: 活性化関数（デフォルトはtanh）
        """
        self.n_input = n_input
        self.n_output = n_output
        self.n_neuron = n_neuron
        self.n_layer = n_layer
        self.epochs = epochs
        self.act_fn = act_fn
        self._loss_values = []  # 損失値の履歴を保存するリスト

    def build(self, optimizer, loss_fn, early_stopping):
        """
        モデルの構築
        
        Parameters:
        optimizer: 最適化アルゴリズム
        loss_fn: 損失関数
        early_stopping: 早期停止の条件
        """
        self._model = MLP(self.n_input, self.n_output, self.n_neuron, self.n_layer, self.act_fn)
        self._optimizer = optimizer
        self._loss_fn = loss_fn
        self._early_stopping = early_stopping
        return self

    def train_step(self, t_data, x_data):
        """
        1ステップの学習を実行
        
        Parameters:
        t_data: 時間データ
        x_data: 教師データ
        """
        # 勾配の計算
        with tf.GradientTape() as tape:
            x_pred = self._model(t_data)  # モデルの予測
            loss = self._loss_fn(x_pred, x_data)  # 損失の計算
        # 勾配を用いたパラメータの更新
        gradients = tape.gradient(loss, self._model.trainable_variables)
        self._optimizer.apply_gradients(zip(gradients, self._model.trainable_variables))
        self._loss_values.append(loss)
        return self

    def train(self, t_data, x_data):
        self._loss_values = []
        for i in range(self.epochs):
            self.train_step(t_data, x_data)
            if self._early_stopping(self._loss_values[-1]):
                break

class PhysicsInformedNNs:
    def __init__(self, n_input, n_output, n_neuron, n_layer, epochs, act_fn='tanh'):
        """
        物理情報を考慮したニューラルネットワークの初期化
        （DataDrivenNNsと同じパラメータ構成）
        """
        self.n_input = n_input
        self.n_output = n_output
        self.n_neuron = n_neuron
        self.n_layer = n_layer
        self.epochs = epochs
        self.act_fn = act_fn
        self._loss_values = []

    def build(self, optimizer, loss_fn, early_stopping):
        """
        モデルの構築（DataDrivenNNsと同じ構造）
        """
        self._model = MLP(self.n_input, self.n_output, self.n_neuron, self.n_layer, self.act_fn)
        self._optimizer = optimizer
        self._loss_fn = loss_fn
        self._early_stopping = early_stopping
        return self

    def train_step(self, t_data, x_data, t_pinn, c, k):
        """
        物理法則を考慮した1ステップの学習を実行
        
        Parameters:
        t_data: 時間データ
        x_data: 教師データ
        t_pinn: 物理法則を適用する時間点
        c: 減衰係数
        k: バネ定数
        """
        with tf.GradientTape() as tape_total:
            tape_total.watch(self._model.trainable_variables)
            # データに基づく損失の計算
            x_pred = self._model(t_data)
            loss1 = self._loss_fn(x_pred, x_data)
            loss1 = tf.cast(loss1, dtype=tf.float32)

            # 物理法則に基づく損失の計算
            with tf.GradientTape() as tape2:
                tape2.watch(t_pinn)
                with tf.GradientTape() as tape1:
                    tape1.watch(t_pinn)
                    x_pred_pinn = self._model(t_pinn)
                dx_dt = tape1.gradient(x_pred_pinn, t_pinn)    # 1階微分
            dx_dt2 = tape2.gradient(dx_dt, t_pinn)            # 2階微分

            # データ型の統一
            dx_dt = tf.cast(dx_dt, dtype=tf.float32)
            dx_dt2 = tf.cast(dx_dt2, dtype=tf.float32)
            x_pred_pinn = tf.cast(x_pred_pinn, dtype=tf.float32)

            # 物理法則（運動方程式）に基づく損失
            loss_physics = dx_dt2 + c * dx_dt + k * x_pred_pinn
            loss2 = 5.0e-4 * self._loss_fn(loss_physics, tf.zeros_like(loss_physics))
            loss2 = tf.cast(loss2, dtype=tf.float32)

            # 総損失の計算
            loss = loss1 + loss2

        # 勾配を用いたパラメータの更新
        self._optimizer.minimize(loss, self._model.trainable_variables, tape=tape_total)
        self._loss_values.append(loss)
        return self

    def train(self, t_data, x_data, t_pinn, c, k):
        self._loss_values = []
        for i in range(self.epochs):
            self.train_step(t_data, x_data, t_pinn, c, k)
            if self._early_stopping(self._loss_values[-1]):
                break

メイン

# main.pyとして保存

import tensorflow as tf
from data_generator import generate_training_data
from training import DataDrivenNNs, PhysicsInformedNNs, EarlyStopping
import matplotlib.pyplot as plt
import os
from PIL import Image
import io
import numpy as np

# 日本語フォント設定
plt.rcParams['font.family'] = 'IPAexGothic'
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 12

class ModelManager:
    def __init__(self, model_type, n_neuron=32, n_layer=4):
        self.model_type = model_type
        if model_type == "DDNN":
            self.model = DataDrivenNNs(1, 1, n_neuron, n_layer, 1)
        elif model_type == "PINN":
            self.model = PhysicsInformedNNs(1, 1, n_neuron, n_layer, 1)
        
        self.optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
        self.loss_fn = tf.keras.losses.MeanSquaredError()
        self.early_stopping = EarlyStopping(patience=200, verbose=0)
        self.model.build(self.optimizer, self.loss_fn, self.early_stopping)
    
    def save_model(self, path):
        if not os.path.exists(path):
            os.makedirs(path)
        self.model._model.save_weights(f"{path}/{self.model_type}_weights.h5")
    
    def load_model(self, path):
        weights_path = f"{path}/{self.model_type}_weights.h5"
        if os.path.exists(weights_path):
            self.model._model.load_weights(weights_path)
            return True
        return False

def create_frame(t, x_analytical, t_data_ddnn, x_data_ddnn, t_data_pinn, x_data_pinn, 
                x_pred_ddnn, x_pred_pinn, current_step):
    """単一フレームを生成する補助関数"""
    fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
    
    # DDNN予測の可視化
    ax1.plot(t, x_analytical, 'r--', label='減衰方程式', linewidth=2)
    ax1.plot(t, x_pred_ddnn, 'g-', label='DDNN予測', linewidth=2)
    ax1.scatter(t_data_ddnn, x_data_ddnn, c='b', s=50, label='学習データ')
    ax1.set_title(f'DDNN Training (Step {current_step})', fontsize=12)
    ax1.set_ylabel('Position (x)', fontsize=12)
    ax1.grid(True, linestyle='--', alpha=0.7)
    ax1.legend(fontsize=10, loc='upper right')
    ax1.set_ylim(-1.5, 1.5)
    
    # PINN予測の可視化
    ax2.plot(t, x_analytical, 'r--', label='減衰方程式', linewidth=2)
    ax2.plot(t, x_pred_pinn, 'g-', label='PINN予測', linewidth=2)
    ax2.scatter(t_data_pinn, x_data_pinn, c='b', s=50, label='学習データ')
    ax2.set_title(f'PINN Training (Step {current_step})', fontsize=12)
    ax2.set_xlabel('Time (t)', fontsize=12)
    ax2.set_ylabel('Position (x)', fontsize=12)
    ax2.grid(True, linestyle='--', alpha=0.7)
    ax2.legend(fontsize=10, loc='upper right')
    ax2.set_ylim(-1.5, 1.5)
    
    plt.tight_layout()
    
    # プロットをPIL Imageに変換
    buf = io.BytesIO()
    plt.savefig(buf, format='png')
    plt.close()
    buf.seek(0)
    return Image.open(buf)

def create_training_animation(t, x_analytical, t_data_ddnn, x_data_ddnn, 
                            t_data_pinn, x_data_pinn, n_neuron=32, n_layer=4,
                            n_frames=50, duration=100, save_path='training_animation.gif'):
    """学習過程をアニメーションGIFとして保存する関数"""
    
    # モデルマネージャーの初期化
    ddnn_manager = ModelManager("DDNN", n_neuron, n_layer)
    pinn_manager = ModelManager("PINN", n_neuron, n_layer)
    
    # フレームを格納するリスト
    frames = []
    
    # 学習ステップ数の計算（等間隔）
    total_steps = 20000
    steps_per_frame = total_steps // n_frames
    
    try:
        # 各フレームの生成
        for frame in range(n_frames):
            # 現在のステップ数
            current_step = frame * steps_per_frame
            
            # モデルの学習
            for _ in range(steps_per_frame):
                ddnn_manager.model.train_step(t_data_ddnn, x_data_ddnn)
                pinn_manager.model.train_step(t_data_pinn, x_data_pinn, t, 4.0, 400.0)
            
            # 予測の実行
            x_pred_ddnn = ddnn_manager.model._model(t)
            x_pred_pinn = pinn_manager.model._model(t)
            
            # フレームの生成と追加
            frame_image = create_frame(
                t, x_analytical, t_data_ddnn, x_data_ddnn, t_data_pinn, x_data_pinn,
                x_pred_ddnn, x_pred_pinn, current_step
            )
            frames.append(frame_image)
        
        # GIFアニメーションの保存
        if frames:
            frames[0].save(
                save_path,
                save_all=True,
                append_images=frames[1:],
                optimize=False,
                duration=duration,
                loop=0
            )
            print(f"Animation saved to {save_path}")
        
    finally:
        # メモリの解放
        for frame in frames:
            frame.close()

def main():
    # トレーニングデータの生成
    data = generate_training_data()
    
    # アニメーションの作成
    create_training_animation(
        t=data['t'],
        x_analytical=data['x'],
        t_data_ddnn=data['t_data_ddnn'],
        x_data_ddnn=data['x_data_ddnn'],
        t_data_pinn=data['t_data_pinn'],
        x_data_pinn=data['x_data_pinn'],
        n_frames=50,
        duration=100,
        save_path='training_animation.gif'
    )

if __name__ == "__main__":
    main()