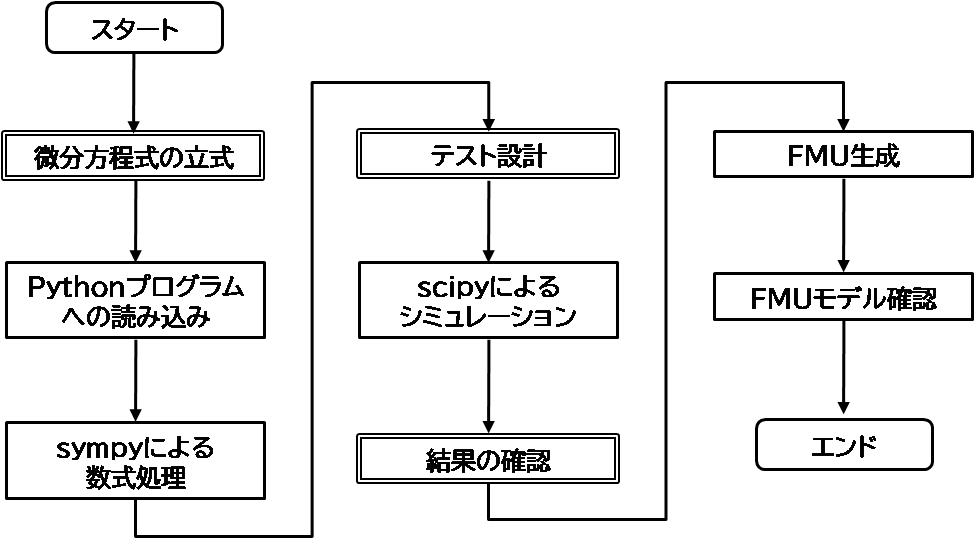0. 初めに
本記事は以下のような読者を想定している
・立式した微分方程式を手っ取り早くシミュレーションしたい
・プログラミングによる1-Dシミュレーションに興味がある
・立式した微分方程式をそのままプラントモデルとしてFMU化したい
・PythonによるFMUを用いたシミュレーションに興味がある
1. 背景
プログラミングやシミュレーションに関する知識はそれ専門の知識が少なからず必要であり、何か物理現象をモデル化してシミュレーションしたい場合、そのモデルを数式処理ツール上で計算できるように準備する必要がある。
そこで、1-Dモデルの構築では、Modelica系物理シミュレーションツールを用いたモデル構築がよく行われるが、ツールやModelicaに関する知識を必要とするほか高価な有償ツールを使う必要が生じ、それがハードルとなることがある。無償ツールであるOpenModelicaを選択することは可能であるが、少なくともツールを使いこなすための訓練は必要である。
(※複雑な事象のモデル化や高度なシミュレーションを行いたい等、有償ツールを使うメリットもある。)
シミュレーション技術の素養向上やさらに多くの人がシミュレーションの世界に足を踏み入れるハードルが下がればと思い、フリーで使えるかつ手軽に色々試すことができるようなシミュレータ環境を提供することが本記事の狙いである。
昨今の生成AIの発展により、プログラミングと生成AIの相性の良さもあり、プログラミングに抵抗があっても最小限の知識(グラフ化等、簡単なプロンプトでも良い回答が得られるレベル)で、より物理現象解明のためのモデル化に注力できるような一助として簡単なプラクティスとして本記事をまとめた。
2. プラクティスの流れ
本プラクティスで実践するフローチャートを以下に示す。フローの2重線の四角枠で囲った箇所が、主にシミュレーション実行者が注力するプロセスであり、その他は後述するプログラムをそのまま利用することを想定する。
シミュレーション実行者が、自身が立式した微分方程式の過渡応答をシミュレーション確認、あるいはパラメータを変化させたときの応答変化を確認するようなユースケースが一例である。以降の章で参考文献を参照しながらひとつユースケースをトライしてみる。
3. シミュレータ環境
作成したプログラムファイル構成を以下に示す。main.pyが各種ファイルよ読み込みながら結果をoutputへ出力する。シミュレーション実行者が主に編集する箇所は、以降の各ファイルの説明にて後述する。
Top/
∟ equation.txt
∟ main.py
∟ lib/
∟ myDslParser.py
∟ myFmuBuilder.py
∟ template/
∟ fmu_template.py.j2
∟ output/ (main.py実行により生成)
∟ equation.py
∟ equation.fmu
3-1. equation.txt
本テキストファイルに、立式した微分方程式を記載する。フローチャートの「微分方程式の立式」に相当する。
本例では、参考文献より、2次元車両の定常円旋回の運動をシミュレーションする例をとり上げる。
地表に固定された2次元座標面における車両重心点の位置$P$($x$, $y$)とし、$x$軸に対するヨー角$\theta$、前輪の横すべり角を$\beta$、ヨー角速度$r$とすると、各状態変数の挙動を記述する微分方程式は以下のように表される。ここで、車速は$V$一定とする。その他はパラメータである。
\begin{align}
\frac{dx}{dt} &= V×cos(\beta+\theta)\\
\frac{dy}{dt} &= V×sin(\beta+\theta)\\
\frac{d\theta}{dt} &= r\\
mV\frac{d\beta}{dt} + 2(K_f+K_r)\beta &+ \Bigl(mV + \frac{2(l_fK_f-l_rK_r)}{V}\Bigr)r = 2K_f\delta_f + 2K_r\delta_r\\
I\frac{dr}{dt} + 2(l_fK_f-l_rK_r)\beta &+ \frac{2(l_f^2K_f+l_r^2K_r)}{V}r = 2l_fK_f\delta_f - 2l_rK_r\delta_r
\end{align}
操作できる入力変数は、前輪操舵角$\delta_f$、後輪操舵角$\delta_r$とする。
(※詳しい式の導出は参考文献の第3章や第8章が参考となる。その他パラメータに関する説明も参考文献を参照)
以下に「equation.txt」の内容を示す。
シミュレーション実行者は、微分される変数や入力変数、パラメータ、式をそのままのイメージで記述する。変数を微分する際は"d()/dt"の()内に変数を記述すればよい。
# =========================
# 状態変数
# =========================
states:
x
y
beta
theta
r
# =========================
# 入力
# =========================
inputs:
delta_f
delta_r
# =========================
# パラメータ
# =========================
parameters:
m = 1500.0
Iz = 2500.0
Kf = 55000.0
Kr = 60000.0
lf = 1.1
lr = 1.6
V = 100.0/3.6
# =========================
# 微分方程式
# =========================
equations:
d(x)/dt = V*cos(beta+theta)
d(y)/dt = V*sin(beta+theta)
m*V*d(beta)/dt + 2*(Kf+Kr)*beta + (m*V + 2*(lf*Kf-lr-Kr)/V)*r = 2*Kf*delta_f + 2*Kr*delta_r
d(theta)/dt = r
Iz*d(r)/dt + 2*(lf*Kf-lr*Kr)*beta + 2*(lf**2*Kf+lr**2*Kr)/V*r = 2*lf*Kf*delta_f - 2*lr*Kr*delta_r
# =========================
# シミュレーション条件
# solver = 'euler' or 'rk2' or 'rk4' for FMU
# =========================
simulation:
t_start = 0.0
t_stop = 30.0
dt = 0.01
solver = rk4
注意点としては、車両のイナーシャ$I$をパラメータで"I"と記述すると、sympyでは虚数iとして認識されるため、"I"という記述を避けるために"Iz"としている。
3-2. main.py
本シミュレータのmainのファイルである。本ファイルを実行すれば、「equation.txt」の内容を読み込み、シミュレーションが実行される。
基本的にシミュレーション実行者が編集する箇所は、どのようなシミュレーションを行いたいかを設計する「3. 評価パターン設計」や、結果をどのようにグラフ化したいか「5. 結果の表示」を編集すればよい。フローチャートでは、「テスト設計」や「結果の確認」に相当する。
# ======================================
# DSL-based Simulator
# ======================================
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
from pathlib import Path
from lib.myDslParser import DslParser
# ======================================
# 0. DSL指定
# ======================================
dsl_path = Path("equation.txt")
model_name = dsl_path.stem
# ======================================
# 1. DSLパースしてモデル構築
# ======================================
parser = DslParser(dsl_path)
parser.parse_blocks()
x, u, rhs_list, rhs = parser.parse_rhs_exec()
# ======================================
# 2. シミュレーション設定
# ======================================
sim_cfg = parser.parse_simulation()
t_start = sim_cfg["t_start"]
t_stop = sim_cfg["t_stop"]
dt = sim_cfg["dt"]
solver = sim_cfg["solver"]
t_eval = np.arange(t_start, t_stop + dt, dt)
# ======================================
# 3. 評価パターン設計
# ======================================
def input_func(t):
return {
"delta_f": 0.04,
"delta_r": 0.0,
}
# ======================================
# 4. SciPy シミュレーション
# ======================================
# 初期条件
y0 = [0.0] * len(x)
# 評価パターンをsympy関数の入力形式に変換
def u_func(t):
return tuple(input_func(t)[s.name] for s in u)
# シミュレーション実行
sol = solve_ivp(
lambda t, y: rhs(t, y, u_func(t)),
(t_start, t_stop),
y0,
t_eval=t_eval
)
# ======================================
# 5. 結果の表示
# ======================================
plt.figure(figsize=(12,4))
# 旋回半径
radius_cal = (max(sol.y[0])-min(sol.y[0]))/2.0
print(f'旋回半径 = {radius_cal}')
# 旋回軌跡の表示
plt.subplot(1,3,1)
plt.plot(sol.y[0], sol.y[1], label="SciPy")
plt.xlabel(x[0].name+str(" [m]"))
plt.ylabel(x[1].name+str(" [m]"))
plt.legend()
plt.grid()
# 横すべり角β
plt.subplot(1,3,2)
plt.plot(sol.t, sol.y[2], label="SciPy")
plt.xlabel("Time [s]")
plt.ylabel(x[2].name+str(" [rad]"))
plt.legend()
plt.grid()
# ヨー角速度r
plt.subplot(1,3,3)
plt.plot(sol.t, sol.y[4], label="SciPy")
plt.xlabel("Time [s]")
plt.ylabel(x[4].name+str(" [rad/s]"))
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
# plt.savefig("./scipy_simulation.png")
3-3. myDslParser.py
「myDslParser.py」の内容を以下に示す。本ファイルは、「equation.txt」に記載された内容を読み取り、Python処理するための各種処理を行う。本ファイルは内容を読み取り後、sympyによる数式を構築する機能まで担う。
from pathlib import Path
import sympy as sp
import numpy as np
class DslParser:
def __init__(self, dsl_path: str | Path):
self.dsl_path = Path(dsl_path)
self.blocks = {}
self.states = []
self.inputs = []
self.parameters = {}
self.state_syms = []
self.input_syms = []
self.derivative_syms = {}
self.equations = []
self.rhs_exprs = {}
self.rhs_list = []
self.sim_cfg = {}
# シンボルとして扱う数学変数を明示的に定義
self.mathFunc = {
"pi": sp.pi,
"sin": sp.sin,
"cos": sp.cos,
"tan": sp.tan,
"asin": sp.asin,
"acos": sp.acos,
"atan": sp.atan,
"atan2": sp.atan2,
"exp": sp.exp,
"log": sp.log,
"sqrt": sp.sqrt,
"abs": sp.Abs
}
def parse_blocks(self):
"""
DSLブロック分解
"""
text = self.dsl_path.read_text()
current = None
for line in text.splitlines():
line = line.strip()
if not line or line.startswith("#"):
continue
if line.endswith(":"):
current = line[:-1]
self.blocks[current] = []
else:
self.blocks[current].append(line)
return self.blocks
def _build_symbols(self):
"""
シンボル生成
"""
# 状態変数のシンボル
self.states = [s.strip() for s in self.blocks["states"]]
self.state_syms = list(sp.symbols(self.states))
# 入力変数のシンボル
self.inputs = [u.strip() for u in self.blocks["inputs"]]
self.input_syms = list(sp.symbols(self.inputs))
# 状態変数の微分のシンボル
self.derivative_syms = list(sp.symbols(f"d{s}_dt") for s in self.states)
# パラメータのシンボル
for line in self.blocks.get("parameters", []):
k, v = line.split("=")
self.parameters[sp.symbols(k.strip())] = eval(v)
return
def _parse_equations(self):
"""
微分方程式の解析
"""
# 状態・入力・微分変数と数学関数をsympy数式解析のシンボルとして追加
local = {s.name: s for s in self.state_syms}
local.update({u.name: u for u in self.input_syms})
local.update({dvar.name: dvar for dvar in self.derivative_syms})
local.update(self.mathFunc)
# DSLに入力された数式の読み込み
for line in self.blocks["equations"]:
lhs, rhs = line.split("=")
lhs = lhs.replace("d(", "d").replace(")/dt", "_dt")
rhs = rhs.replace("d(", "d").replace(")/dt", "_dt")
eq = sp.Eq(
sp.sympify(lhs, locals=local),
sp.sympify(rhs, locals=local),
)
self.equations.append(eq)
return
def _parse_derivatives(self):
"""
微分係数の算出
"""
# 求める微分係数の右辺をsympyで計算
for dvar in self.derivative_syms:
# dvar を含む方程式だけ抽出
related_eqs = [eq for eq in self.equations if eq.has(dvar)]
eq = related_eqs[0]
sol = sp.solve(eq, dvar)
if not sol:
raise ValueError(f"Could not solve equation for {dvar}")
self.rhs_exprs[dvar.name] = sol[0]
# パラメータの値を代入
self.rhs_list = [self.rhs_exprs[dvar.name].subs(self.parameters) for dvar in self.derivative_syms]
return
def parse_rhs_exec(self):
"""
読み込んだDLSの内容からモデルを構築する
"""
self._build_symbols()
self._parse_equations()
self._parse_derivatives()
# 関数化
f_rhs = sp.lambdify((*self.state_syms, *self.input_syms), self.rhs_list, "numpy")
def rhs(t, y, u):
return np.asarray(f_rhs(*y, *u), dtype=float)
return (
self.state_syms,
self.input_syms,
self.rhs_list,
rhs
)
def parse_simulation(self):
for line in self.blocks.get("simulation", []):
k, v = line.split("=")
k = k.strip()
v = v.strip()
try:
self.sim_cfg[k.strip()] = float(v)
except:
# 数値でなければ文字列(例: rk4)
self.sim_cfg[k.strip()] = str(v).lower()
return self.sim_cfg
(とりあえず動かしてみたい方はコピペで準備で良い。)
3-4. myFmuBuilder.py
「myFmuBuilder.py」の内容を以下に示す。本ファイルは、sympyにり構築した微分方程式をPython FMU に出力すためのPythonスクリプトおよびFMUファイルを生成する機能を担う。Pythonスクリプトはテンプレート処理として後述する「fmu_template.py.j2」テンプレート記述ファイルとセットで使用する。
from pathlib import Path
import sympy as sp
from jinja2 import Environment, FileSystemLoader
from pythonfmu import FmuBuilder
class SympyToFmuBuilder:
def __init__(
self,
model_name: str,
states: list[sp.Symbol],
inputs: list[sp.Symbol],
rhs_exprs: list[sp.Expr],
solver: str,
template_dir: Path,
output_dir: Path
):
self.model_name = model_name
self.states = states
self.inputs = inputs
self.rhs_exprs = rhs_exprs
self.solver = solver
self.template_dir = template_dir
self.output_dir = output_dir
self.rhs_code = ""
self.py_file = None
self.fmu_file = None
return
def _generate_rhs_code(self):
"""
sympy → Pythonコード変換
sympyのシンボルをPythonのFMUクラスで計算できるようにself.*へ変換する
"""
rhs_code = []
for s, expr in zip(self.states, self.rhs_exprs):
e = expr
for ss in self.states:
e = e.subs(ss, sp.Symbol(f"self.{ss.name}"))
for uu in self.inputs:
e = e.subs(uu, sp.Symbol(f"self.{uu.name}"))
rhs_code.append(f"{s.name}_dot = {sp.pycode(e)}")
self.rhs_code = rhs_code
return
def _generate_fmu_pyfile(self) -> Path:
"""
FMU用Pythonファイル生成
レンダリング用のテンプレートファイル: fmu_template.py.j2
"""
# --- Jinja2 環境 ---
env = Environment(
loader=FileSystemLoader(self.template_dir),
trim_blocks=True,
lstrip_blocks=True
)
# --- レンダリング ---
template = env.get_template("fmu_template.py.j2")
fmu_code = template.render(
model_name=self.model_name,
states=[s.name for s in self.states],
inputs=[u.name for u in self.inputs],
rhs_code=self.rhs_code,
solver=self.solver
)
# --- 書き出し ---
py_file = self.output_dir / f"{self.model_name}.py"
py_file.write_text(fmu_code)
self.py_file = py_file
return
def _build_fmu(self) -> Path:
"""
FMUビルド
"""
FmuBuilder.build_FMU(self.py_file, dest=self.output_dir)
self.fmu_file = self.output_dir / f"{self.model_name}.fmu"
return
def main(self):
"""
微分方程式をPythonファイル化してFMU生成する
生成したFMUモデルへのパスをリターンする
"""
# 生成物格納用フォルダ生成
self.output_dir.mkdir(exist_ok=True)
self._generate_rhs_code()
self._generate_fmu_pyfile()
self._build_fmu()
return self.fmu_file
(とりあえず動かしてみたい方はコピペで準備で良い。)
3-5. fmu_template.py.j2
「fmu_template.py.j2」の内容を以下に示す。本ファイル、PythonFMU生成用の処理テンプレートである。シミュレーション実行者により入力された数式を自動で記載するためのJinja2用テンプレートである。FMUで計算する微分方程式の定義や積分ソルバーを記載している。積分ソルバーは教科書等でもよくあるオイラー法やルンゲクッタ法を用意している。
(オイラー法やルンゲクッタ法の記事については こちら )
from pythonfmu import Fmi2Slave, Real, Fmi2Causality
import numpy as np
import math
class {{ model_name }}(Fmi2Slave):
def __init__(self, **kwargs):
super().__init__(**kwargs)
{% for s in states %}
self.{{ s }} = 0.0
{% endfor %}
{% for u in inputs %}
self.{{ u }} = 0.0
{% endfor %}
# FMU Input/Output port setting
{% for u in inputs %}
self.register_variable(Real("{{ u }}", causality=Fmi2Causality.input))
{% endfor %}
{% for s in states %}
self.register_variable(Real("{{ s }}", causality=Fmi2Causality.output))
{% endfor %}
# FMU solver setting
self.solverTable = {
"euler": self.solver_euler,
"rk2": self.solver_rk2,
"rk4": self.solver_rk4
}
self.solver = self.solverTable["{{ solver }}"]
def rhs(self, x, t):
{% for s in states %}
self.{{ s }} = x[{{ loop.index0 }}]
{% endfor %}
{% for line in rhs_code %}
{{ line }}
{% endfor %}
return np.array([
{% for s in states %}
{{ s }}_dot,
{% endfor %}
], dtype=float)
def solver_euler(self, x, t, h):
f = self.rhs
x_new = x + h*f(x, t)
return x_new
def solver_rk2(self, x, t, h):
f = self.rhs
k1 = f(x, t)
k2 = f(x+k1*h, t+h)
x_new = x + h*(k1+k2)*0.5
return x_new
def solver_rk4(self, x, t, h):
f = self.rhs
k1 = f(x, t)
k2 = f(x+k1*h*0.5, t+h*0.5)
k3 = f(x+k2*h*0.5, t+h*0.5)
k4 = f(x+k3*h, t+h)
x_new = x + h*(k1+2.0*k2+2.0*k3+k4)/6.0
return x_new
def do_step(self, current_time, step_size):
# current values
x = np.array([
{% for s in states %}
self.{{ s }},
{% endfor %}
], dtype=float)
# integration
x_new = self.solver(x, current_time, step_size)
# updated values
{% for s in states %}
self.{{ s }} = x_new[{{loop.index0}}]
{% endfor %}
return True
(とりあえず動かしてみたい方はコピペで準備で良い。)
3-6. シミュレーション確認
上記までに掲載したプログラムを実行すると以下結果が得られた。図の左は車両の重心点$P$($x$, $y$)の軌跡、真ん中は横すべり角$\beta$、右はヨー角速度$r$の応答結果を示す。$P$($x$, $y$)の軌跡は($0$, $0$)をスタート地点とし、反時計回りに速度$V$を与えた時に描く軌跡となっており、円旋回できていることが確認できる。
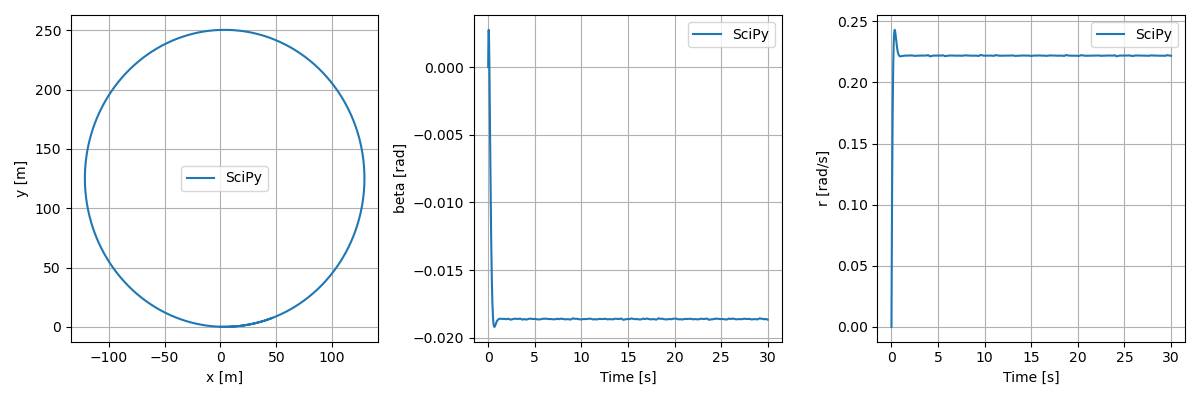
定常時の旋回半径$\rho$は以下式で表される。(※詳しい式の導出やパラメータの説明は参考文献の第3章を参照)
\begin{align}
\rho &= \Bigl(1-\frac{m}{2l^2}\frac{l_fK_f-l_rK_r}{K_fK_r}V^2\Bigr)\frac{l}{\delta} \\
\end{align}
上記式で計算した結果と、シミュレーションで得られた軌跡のx軸方向直径/2で算出した旋回半径は概ね$125$[m]で一致した。
4. sympy数式をFMU化してシミュレーション
立式した微分方程式の応答が確認できたので、これをPython FMU化する手続きを実行する。
main.py に以下のプログラムを追加する。フローチャートの「FMU生成」と「FMUモデル確認」に相当する。
基本的にシミュレーション実行者が編集する箇所は、結果をどのように確認したいかに応じてグラフ化処理を編集すればよく、今回はscipyによる数値シミュレーションと、FMU化したモデルが同じ動作をするかを確認するという例として、scipyによるシミュレーション結果とFMUモデルによるシミュレーション結果を重ね合わせて表示することで確認する「8. 結果の重ね合わせ」のような処理とした。
from fmpy import simulate_fmu
from lib.myFmuBuilder import SympyToFmuBuilder
# ======================================
# 6. FMU生成
# ======================================
template_path = Path("templates")
output_path = Path("outputs")
fmubuilder = SympyToFmuBuilder(
model_name=model_name,
states=x,
inputs=u,
rhs_exprs=rhs_list,
solver=solver,
template_dir=template_path,
output_dir=output_path
)
fmu_path = fmubuilder.main()
# ======================================
# 7. FMU シミュレーション
# ======================================
# 評価パターンをFMUの入力形式に変換
dtype = [('time', np.float64)] + [(s.name, np.float64) for s in u]
u_fmu = np.zeros(len(t_eval), dtype=dtype)
u_fmu['time'] = t_eval
for i,t in enumerate(t_eval):
for s in u:
u_fmu[s.name][i] = input_func(t)[s.name]
# FMUのシミュレーション実行
result = simulate_fmu(
fmu_path,
start_time=t_start,
stop_time=t_stop,
# step_size=dt,
output_interval=dt,
input=u_fmu
)
# ======================================
# 8. 結果の重ね合わせ
# ======================================
plt.subplot(1,3,1)
plt.plot(result[x[0].name], result[x[1].name], "--", label="FMU")
plt.legend()
plt.subplot(1,3,2)
plt.plot(result["time"], result[x[2].name], "--", label="FMU")
plt.legend()
plt.subplot(1,3,3)
plt.plot(result["time"], result[x[4].name], "--", label="FMU")
plt.legend()
# plt.savefig("./scipy_simulation.png")
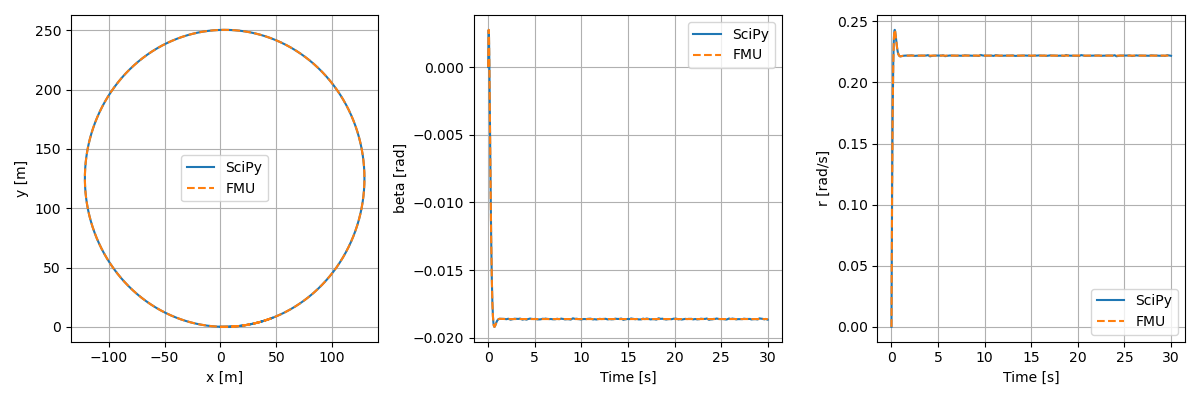
シミュレーション結果を以下図に示す。先のscipyシミュレーション結果の上に、FMUモデルのシミュレーション結果を橙色破線で示した。両者はよく一致しており、立式した通りの微分方程式がFMUに実装できていることが分かる。
5. FMUをプラントモデルとした制御系シミュレーション
ここではさらに、立式した微分方程式を実装したFMUをプラントモデルと見立て、制御系を構築した際のシミュレーション実施例を示す。
ここでは制御例として、参考文献に記載の、横すべり零化後輪操舵制御を構築してプラントモデルと接続し、シミュレーションをする例を実施する。
横すべり零化後輪操舵制御則
これまで立式した微分方程式の入力である後輪操舵角$\delta_r$は何もしない(=$0$)を代入してきた。そこで、ここでは、横すべり角$\beta$が常に$0$となるように後輪操舵角$\delta_r$を制御するコントローラを追加する。制御則は以下式で与えられる。(※詳しい式の導出やパラメータの説明は参考文献の第8章を参照)
\begin{align}
\delta_f &= \frac{1}{n}\delta \\
\delta_r &= k_{\delta}\delta_f + k_rr\\
※k_{\delta} &= -\frac{K_f}{K_r}\\
※k_r &= \frac{mV^2+2(l_fK_f-l_rK_r)}{2K_rV}
\end{align}
制御系を含めたシミュレーション構成を図示化すると以下のようになる。ハンドル操舵角$\delta$とヨー角速度$r$を用いて制御入力となる前後輪操舵角$\delta_f$,$\delta_r$を計算するコントローラにより、プラントモデルを制御する。
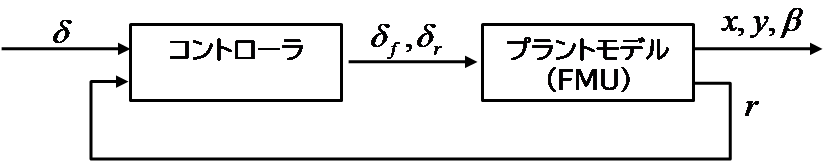
上図のシミュレーションをPythonプログラムで実装した例を以下に示す。
以前の章で用いたFMUシミュレーションは、fmpyモジュールのsimulate_fmuにてシミュレーション実行していたが、こちらを使用する場合は、各時刻での入力値を事前に与える(フィードフォワード)シミュレーションとなっている。
しかし今回の制御則では、モデルの出力であるヨー角速度$r$をフィードバックして入力を計算する必要がある。よって、フィードバック系の制御則を構築する場合は、各時刻の計算を1ステップずつ進め、前回のモデル出力値を用いて今回のステップの入力を計算する必要がある。(この手続きは、プログラム中盤のfor文 "for t in t_eval:" 内にて実現している。)
上記の制御則は、controller関数に実装している。後輪操舵角を計算するための係数$k_{\delta}$,$k_r$はプログラム簡単化のため事前に計算した値を記述してある。
# ======================================
# FMUを用いた横すべり零化後輪操舵制御の例
# ======================================
from fmpy import read_model_description, extract
from fmpy.fmi2 import FMU2Slave
# FMU初期化
unzipdir = extract(fmu_path)
model_description = read_model_description(fmu_path)
fmu = FMU2Slave(
guid=model_description.guid,
unzipDirectory=unzipdir,
modelIdentifier=model_description.coSimulation.modelIdentifier,
instanceName='constantRadius'
)
fmu.instantiate()
fmu.setupExperiment(startTime=t_start)
fmu.enterInitializationMode()
fmu.exitInitializationMode()
# モデル変数の取得
vr = {v.name: v.valueReference for v in model_description.modelVariables}
# 入力
input_handle = 0.04
n = 1
def controller(handle, r):
k_delta = -0.91667
k_r = 0.325922
delta_f = handle/n
delta_r = k_delta*delta_f + k_r*r
return delta_f, delta_r
# ログ初期化
result_log = {k: [] for k in vr.keys()}
result_log['time'] = []
# シミュレーションループ
t_eval = np.arange(0.0, 50.0 + dt, dt)
for t in t_eval:
# --- ログ ---
result_log['time'].append(t)
for k in vr.keys():
result_log[k].append(fmu.getReal([vr[k]])[0])
# --- 出力値の取得 ---
r = fmu.getReal([vr['r']])[0]
# --- 制御入力決定 ---
delta_f, delta_r = controller(input_handle, r)
# --- FMUプラントモデルに入力値を設定 ---
fmu.setReal(
[vr['delta_f'], vr['delta_r']],
[delta_f, delta_r]
)
# --- 1ステップ進める ---
fmu.doStep(
currentCommunicationPoint=t,
communicationStepSize=dt
)
# 結果表示
plt.figure(figsize=(12,4))
# 旋回軌跡の表示
plt.subplot(1,3,1)
plt.plot(result[x[0].name], result[x[1].name], label='δr=0.0')
plt.plot(result_log[x[0].name], result_log[x[1].name], label='δr=controlled')
plt.xlabel(x[0].name+str(" [m]"))
plt.ylabel(x[1].name+str(" [m]"))
plt.legend()
plt.grid()
# 横すべり角β
plt.subplot(1,3,2)
plt.plot(sol.t, sol.y[2], label="SciPy")
plt.plot(result_log["time"], result_log[x[2].name])
plt.xlabel("Time [s]")
plt.xlim([0,30])
plt.ylabel(x[2].name+str(" [rad]"))
plt.grid()
# ヨー角速度r
plt.subplot(1,3,3)
plt.plot(result["time"], result[x[4].name])
plt.plot(result_log["time"], result_log[x[4].name])
plt.xlabel("Time [s]")
plt.xlim([0,30])
plt.ylabel(x[4].name+str(" [rad/s]"))
plt.grid()
plt.tight_layout()
plt.show()
# plt.savefig("./controller_simulation.png")
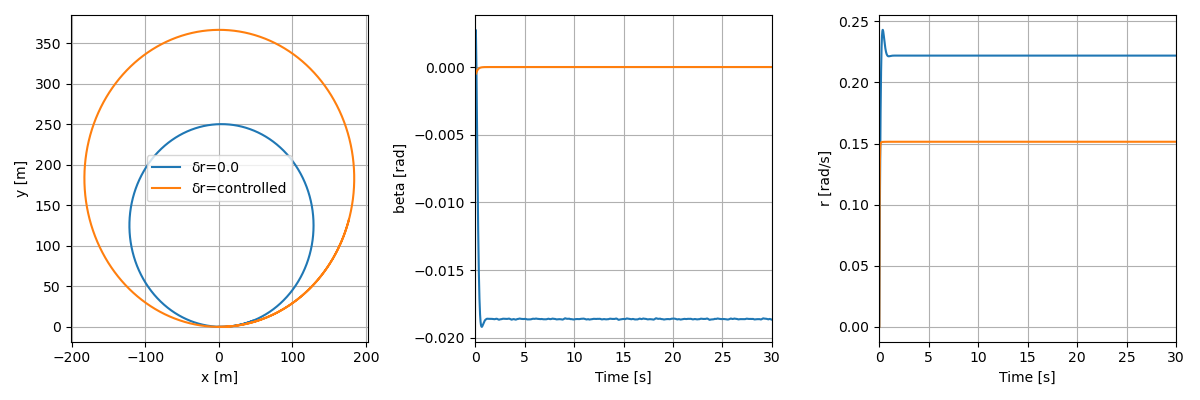
シミュレーション結果を以下図に示す。青の実線は先のFMUモデルのシミュレーション結果(後輪操舵制御なし)を示し、橙色の実線は横すべり角が$0$となるように後輪操舵角の制御則を追加したシミュレーション結果である。横すべり角$\beta$は下図の真ん中に示しており、制御則を追加することによって概ね$0$にできていることが確認できる。
参考文献
安部正人著.「自動車の運動と制御 第2版」東京電機大学出版局.2012年