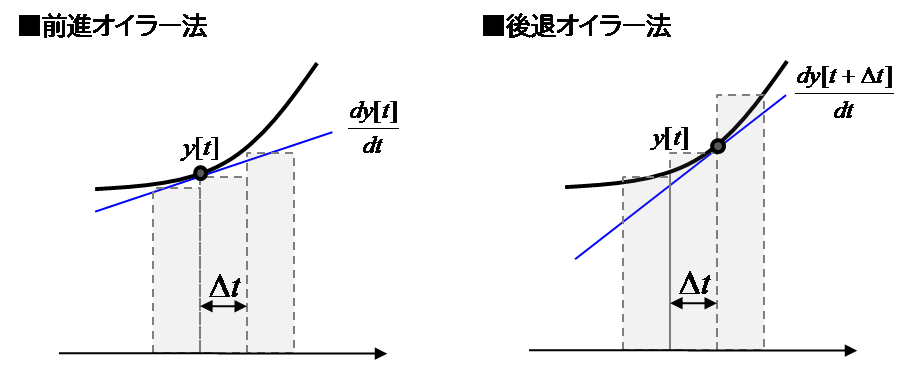
微分方程式の時刻歴応答の数値計算の基本
微分方程式をコンピュータによって計算するための基本は、離散時間において数値積分を実施することである。最も基本的な解法がオイラー法となる。
【前進オイラー法】
連続関数の$y(t)$を離散化し、計算ステップを$Δt$、 $t = n×Δt (n:タイムステップ数)$ の $y(t)$ を $y[t]$ として離散時間積分を行う手法で、将来の値を計算するために現在の値のみを使用するものが前進オイラー法である。
\begin{align}
y[t+Δt] &= y[t] + Δt×\frac{dy[t]}{dt} \\
\end{align}
(※$dy[t]/dt$ は、時刻$t$における$y(t)$の微分係数とする。)
前進オイラー法は、$y[t+Δt]$ を計算するのに $y[t]$ しか必要としないので順番に計算していけばおのずと解が得られる。こうした手法を「陽解法」と呼ぶ。
【後退オイラー法】
後退オイラー法は、微分係数に将来の値を用いる。
\begin{align}
y[t+Δt] &= y[t] + Δt×\frac{dy[t+Δt]}{dt} \\
\end{align}
$y[n+1]$ を計算するのに必要な $dy[n+1]/dt$ に $y[n+1]$が含まれているように、将来の値を用いて次のステップを計算する手法を「陰解法」と呼ぶ。
離散積分の高精度化
上記で見た解法は連続関数の積分値を離散時間間隔の長方形で近似した計算方法となるので誤差が発生する。
例えば上記の$y$が位置を表す変数であった場合、$dy/dx$は速度を表すが、ステップ間で速度が一定であると近似していることに相当する。実際は関数の曲線のように徐々に変化しているためこの変化が考慮できていない。よって、ステップ間に変化する量に対してどのように近似精度を上げるかといった観点で種々の積分公式の修正を行う。次数を上げた補間関数を利用することがよく行われている。
【台形法】
ステップ間の面積を台形に近似した積分公式とするのが台形法である。
\begin{align}
y[t+Δt] &= y[t] + Δt×\frac{\frac{dy[t]}{dt}+\frac{dy[t+Δt]}{dt}}{2} \\
\end{align}
【シンプソンの公式の利用】
\begin{align}
y[t+Δt] &= y[t] + Δt×\frac{\frac{dy[t]}{dt}+4\frac{dy[t+Δt/2]}{dt}+\frac{dy[t+Δt]}{dt}}{6} \\
\end{align}
近似精度の確認
上記の公式に対して、$[t+Δt/a]$ ($a=1or2$) 時点の量に対して前進オイラーの式で展開し、変形していくと以下のようになる。
【台形公式】
まず、右辺第2項の分子で登場している以下の項を前進オイラーの式で展開する。
\begin{align}
\frac{dy[t+Δt]}{dt} &= \frac{y[t]}{dt} + Δt×\frac{d^2y[t]}{dt^2} \\
\end{align}
上式を積分公式に代入すると以下のようになる。
\begin{align}
y[t+Δt] &= y[t] + Δt×\frac{\frac{dy[t]}{dt}+\frac{y[t]}{dt} + Δt×\frac{d^2y[t]}{dt^2}}{2} \\
&= y[t] + Δt×\frac{dy[t]}{dt} + \frac{Δt^2}{2}×\frac{d^2y[t]}{dt^2} \\
&= y[t] + \frac{1}{1!}\frac{dy[t]}{dt}Δt + \frac{1}{2!}\frac{d^2y[t]}{dt^2}Δt^2
\end{align}
【シンプソンの公式の利用】
まず、右辺第2項の分子で登場している以下の項を前進オイラーの式で展開する。
\begin{align}
\frac{dy[t+Δt/2]}{dt} &= \frac{y[t]}{dt} + \frac{Δt}{2}×\frac{d^2y[t]}{dt^2} \\
\end{align}
\begin{align}
\frac{dy[t+Δt]}{dt} &= \frac{y[t]}{dt} + Δt×\frac{d^2y[t]}{dt^2} \\
\end{align}
上式を積分公式に代入すると以下のようになる。
\begin{align}
y[t+Δt] &= y[t] + Δt×\frac{\frac{dy[t]}{dt}+4\frac{dy[t+Δt/2]}{dt}+\frac{dy[t+Δt]}{dt}}{6} \\
&= y[t] + Δt×\frac{\frac{dy[t]}{dt}+4(\frac{y[t]}{dt} + \frac{Δt}{2}×\frac{d^2y[t]}{dt^2})+(\frac{y[t]}{dt} + Δt×\frac{d^2y[t]}{dt^2})}{6} \\
&= y[t] + \frac{Δt}{6}×\frac{dy[t]}{dt}+\frac{2Δt}{3}×\frac{dy[t]}{dt}+\frac{Δt^2}{3}×\frac{d^2y[t]}{dt^2}+\frac{Δt}{6}×\frac{dy[t]}{dt}+\frac{Δt^2}{6}×\frac{d^2y[t]}{dt^2}\\
&= y[t] + Δt×\frac{dy[t]}{dt} + \frac{Δt^2}{2}×\frac{d^2y[t]}{dt^2} \\
&= y[t] + \frac{1}{1!}\frac{dy[t]}{dt}Δt + \frac{1}{2!}\frac{d^2y[t]}{dt^2}Δt^2
\end{align}
両式ともに、$y[t+Δt]$のテイラー展開を2階微分係数の項までで打ち消した式となっている。オイラー法は同観点でいうと1階微分係数の項まで採用した式ととらえることができる。
つまり、数値積分の公式の精度は、「数値積分する物理量の時刻$t$時点まわりでテイラー展開したときに何次の微分係数まで適合しているか」で計算精度が決まっている。
ルンゲクッタ法 (4次の近似精度)
ルンゲクッタ法(固定ステップの4次の公式)の計算式は以下となる。ルンゲクッタ法には近似次数にバリエーションがあるため様々なバリエーションの名称があるが、一般的な「ルンゲクッタ法」と称されるのは以下の4次近似精度を持つ公式となる。$dy/dt=f(t,y)$とする。
\begin{align}
k_1 &= f(t, y[n]) \\
k_2 &= f \Bigl( t+\frac{Δt}{2}, y[n]+\frac{Δt}{2}k_1 \Bigr) \\
k_3 &= f \Bigl( t+\frac{Δt}{2}, y[n]+\frac{Δt}{2}k_2 \Bigr) \\
k_4 &= f(t+Δt, y[n]+Δtk_3) \\
y[t+Δt] &= y[t]+Δt×\frac{k_1+2k_2+2k_3+k_4}{6}
\end{align}
[参考余談]
埋め込み型ルンゲクッタ法としてルンゲクッタフェールベルク法やルンゲクッタドルマンプリンス法があり、可変ステップ計算の数値計算手法である。ルンゲクッタドルマンプリンス法は、積分結果として出力する用の積分公式の次数は4次、誤差比較用で次数5次の積分値を8個の微分係数値($k_1~k_8$)から作り、出力用の積分値と誤差比較用の積分値を使って次ステップサイズを決定する。Simulinkの可変ステップのデフォルトソルバー(ode45)とされるなど広く使われている。ode23など、略称から積分次数(前の数字2が出力値の積分次数、後ろの数字3が誤差比較用の積分次数)が分かるような表記もよく見かける。固定ステップのルンゲクッタドルマンプリンス法(ode8)は8個の微分係数を使うが近似次数は6次までしか達成できない。計算する微分係数と近似精度が比例するのは4次までであるので、精度と計算効率の観点で4次ルンゲクッタの計算公式が広く使われている理由である。
近似精度の確認
ルンゲクッタ法の計算が時刻$t$時点まわりでテイラー展開したときの4次まで適合しているかを確認する。確認のために簡単な微分方程式の例を用いて説明する。以下の微分方程式を考える。
\frac{dy}{dt} = \lambda y
この微分方程式を満たす$y$は以下のようになる。(※初期条件としてy(0)=1とする)
y(t) = e^{\lambda t}
ここで、関数$e^x$のテイラー展開(マクローリン展開)は以下のような形式となる。
e^x = 1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+…
上記の$y$式について、離散時刻$t+Δt$時点の式を以下のような形に変形する。
\begin{align}
y[t+Δt] &= e^{\lambda (t+Δt)} \\
&= e^{\lambda t}e^{\lambda Δt} \\
&= y[t]×\Bigl( 1+\frac{\lambda Δt}{1!}+\frac{(\lambda Δt)^2}{2!}+\frac{(\lambda Δt)^3}{3!}+… \Bigr) \\
\end{align}
上記の乗算第2項目が級数展開で続いていく。ルンゲクッタ法の計算式を代入してみて、上記の級数展開が4次の項まで合致しているかを確認する。
確認に際しては手計算でもよいが、自身のPythonプログラムの勉強もかねてPythonによる計算を行った。プログラムを以下に示す。
import sympy as sp
t, y, tn, yn, yn1, dt, lmd = sp.symbols('t y tn, yn, yn1, dt lmd')
derFunc = lmd*y
f = sp.lambdify((t, y), derFunc, "numpy")
k1 = f(tn, yn)
k2 = f(tn+dt/2, yn+k1*dt/2)
k3 = f(tn+dt/2, yn+k2*dt/2)
k4 = f(tn+dt, yn+k3*dt)
yn1 = yn + dt*(k1+2*k2+2*k3+k4)/6
# print(yn1)
yn1 = sp.factor_terms(sp.expand(yn1), clear=False)
print(yn1)
[プログラムの簡単な説明]
t, y, tn, yn, yn1, dt, lmd = sp.symbols('t y tn, yn, yn1, dt lmd')
代数演算できるようにまずsp.simbolsで文字の定義を行う。
t, y: 微分関数$f(t,y)$のt, yを示す。
tn, yn: 時刻$t$時点の時刻とその出力値。上文字との重複を避けるためだが、説明中の$t$と$y[t]$に該当する。
yn1: 時刻$t+Δt$時点の出力値。説明中の$y[t+Δt]$に該当する。
dt: $Δt$ を示す。
lmd: $e^{\lambda t}$の$\lambda$を示す。
derFunc = lmd*y
f = sp.lambdify((t, y), derFunc, "numpy")
derFunc変数に、今回の微分計算の関数$f$の定義式である$\lambda y$の式を記入する。sp.lamdififyの第3引数に"numpy"を指定すると、Numpyのユニバーサル関数オブジェクトufunc(np.sinのような関数)に変換してくれる。変換してほしい式を第2引数に渡し、その時の変数をリストで第1引数に渡す。
今回は$f(t,y)$のため、関数の変数は$t$と$y$をリストにして第1引数に渡し、先ほど定義した微分関数変数derFuncを第2引数に渡し、ufuncタイプの関数fを作成している。
k1 = f(tn, yn)
k2 = f(tn+dt/2, yn+k1*dt/2)
k3 = f(tn+dt/2, yn+k2*dt/2)
k4 = f(tn+dt, yn+k3*dt)
yn1 = yn + dt*(k1+2*k2+2*k3+k4)/6
ここで、実際のルンゲクッタ法による計算を行っている。
yn1 = sp.factor_terms(sp.expand(yn1), clear=False)
出力結果の見やすさのため、一度()式を展開(sp.expand)し、共通項のynを()でくくる(sp.factor_terms)。
[プログラムの出力結果]
実行した際のyn1の出力結果は以下のようになった。
yn*(dt**4*lmd**4/24 + dt**3*lmd**3/6 + dt**2*lmd**2/2 + dt*lmd + 1)
上式を以下のように書くと$y=e^{\lambda y}$のテイラー展開の4次の項までの形となっていることが分かる。
\begin{align}
実行結果 &= y[n]×(Δt^4\lambda ^4/24 + Δt^3\lambda ^3/6 + Δt^2\lambda ^2/2 +Δt\lambda +1) \\
&= y[n]×\Bigl( 1+\frac{\lambda Δt}{1!}+\frac{(\lambda Δt)^2}{2!}+\frac{(\lambda Δt)^3}{3!}+\frac{(\lambda Δt)^4}{4!} \Bigr) \\
\end{align}
Pythonによるシミュレーション確認
Pythonによるオイラー法、ルンゲクッタ法の計算シミュレーションで動作を確認してみる。なお、解析解と比較できるよう簡単な1次元の振動問題を取り上げる。
問題設定
以下のような1自由度の振動モデルを考える。$m$を質点の質量、$c$を減衰、$k$をバネ定数とし、$x$が質点座標を表す。$\dot{x}$は質点速度、$\ddot{x}$は質点の加速度を表し、初期変位$x_0$と初速度$v_0$を与える。

上式の運動方程式は以下となる。
m\ddot{x}+c\dot{x}+kx = 0
解析解
上記式の解析解を求めておく。一般解を$x=Ae^{st}$と置いて上式に代入し特性方程式を算出すると以下になる。
\begin{align}
ms^2Ae^{st}+csAe^{st}+kAe^{st} &= (ms^2+cs+k)Ae^{st} \\
&= 0\\
\end{align}
振動解を求めるためs=0でない解を求めると以下のようになる。
\begin{align}
s &= \frac{-c±\sqrt{c^2-4mk}}{2m} \\
&= -\frac{c}{2m}±\sqrt{\Bigl(\frac{c}{2m}\Bigr)^2-\frac{k}{m}}
\end{align}
ここで、臨界減衰係数$c_c=2\sqrt{mk}$とし、減衰比$\zeta=c/c_c$、固有振動数$\omega _n=\sqrt{k/m}$として、
\frac{c}{2m}=\frac{c}{2\sqrt{mk}}\frac{2\sqrt{mk}}{2m}=\frac{c}{c_c}\sqrt{\frac{k}{m}}=\zeta \omega _n
より、$s$を以下のように書き換える。ただし、振動解を考えているので、根号内は負であるとして虚数単位$j$とする。
\begin{align}
s &= -\zeta \omega _n ±j\sqrt{\omega _n ^2 - \zeta ^2 \omega _n ^2} \\
&= (-\zeta±j\sqrt{1-\zeta ^2})\omega _n
\end{align}
よって、$x$の一般解は以下のようになる。
\begin{align}
x &= A_1e^{(-\zeta+j\sqrt{1-\zeta ^2})\omega _nt} + A_2e^{(-\zeta-j\sqrt{1-\zeta ^2})\omega _nt} \\
&= e^{-\zeta\omega _nt}\Bigl(A_1e^{j\sqrt{1-\zeta ^2}\omega _nt} + A_2e^{-j\sqrt{1-\zeta ^2}\omega _nt} \Bigr) \\
&= e^{-\zeta\omega _nt}\Bigl((A_1+A_2)cos\sqrt{1-\zeta ^2}\omega _nt +j(A_1-A_2)sin\sqrt{1-\zeta ^2}\omega _nt\Bigr) \\
&= e^{-\zeta\omega _nt}(A_3cos\omega _dt +A_4sin\omega _dt) \\
&= Ae^{-\zeta\omega _nt}cos(\omega _dt - \phi)
\end{align}
ただし、
\begin{align}
\omega _d &= \sqrt{1-\zeta ^2}\omega _n \\
A &= \sqrt{A_3 ^2 + A_4 ^2} \\
\phi &= tan^{-1}\Bigl(\frac{A_4}{A_3}\Bigr)
\end{align}
とする。初期条件を与えて上記$A$と$\phi$を算出する。まず、$t=0$の時、$x=x_0$より、
A_3 = x_0
初期条件$v_0$を与えるために、$x$の微分をすると以下のようになる。
\begin{align}
v &= -\zeta\omega _ne^{-\zeta\omega _nt}(A_3cos\omega _dt +A_4sin\omega _dt)+e^{-\zeta\omega _nt}(-A_3sin\omega _dt +A_4cos\omega _dt)\omega _d \\
v(t=0) &= v_0\\
&= -\zeta\omega _nA_3+A_4\omega _d \\
&= -\zeta\omega _nx_0+A_4\omega _d
\end{align}
よって、
A_4 = \frac{\zeta\omega _nx_0+v_0}{\omega _d}
まとめると、解析解は以下のようになる。
\begin{align}
x &= Ae^{-\zeta\omega _nt}cos(\omega _dt - \phi) \\
A &= \sqrt{x_0^2 + \Bigl(\frac{\zeta\omega _nx_0+v_0}{\omega _d} \Bigr)^2} \\
\phi &= tan^{-1}\Bigl(\frac{\zeta\omega _nx_0+v_0}{x_0 \omega _d}\Bigr)
\end{align}
微分方程式の1階微分表現への変形
数値計算を行うに際し、今回の例の2階微分方程式の形では数値計算できないので、1階微分の形に変形する。加速度は速度の1階微分、速度は位置の1階微分なので、速度と位置のベクトル変数を準備し、ベクトル変数の1階微分で加速度と速度を表現する状態方程式を立てる。
\dot{
\left[
\begin{array}{c}
\dot{x} \\
x
\end{array}
\right]
}
=
\left[
\begin{array}{cc}
-\frac{c}{m} & -\frac{k}{m} \\
1 & 0
\end{array}
\right]
\left[
\begin{array}{c}
\dot{x} \\
x
\end{array}
\right]
作成したPythonプログラム
import numpy as np
import matplotlib.pyplot as plt
cParams = {
"M": 5.0,
"K": 320,
"C": 16,
"X0": 0.05,
"V0": 0.4,
"SIM_START": 0.0,
"SIM_END": 5.0,
"SIM_STEP": 0.005,
}
def calcAnalyticalSolution(t):
# モデルパラメータ設定
m = cParams["M"]
c = cParams["C"]
k = cParams["K"]
v0 = cParams["V0"]
x0 = cParams["X0"]
# 振動パラメータ計算
wn = np.sqrt(k/m) # 不減衰固有角振動数
zeta = c/(2.0*np.sqrt(m*k)) # 減衰比
wd = np.sqrt(1-zeta**2)*wn # 減衰固有角振動数
# 解の計算
Amp = np.sqrt((x0**2 + ((zeta*wn*x0 + v0)/wd)**2))
phi = np.arctan((zeta*wn*x0 + v0)/(x0*wd))
x = Amp*np.exp(-zeta*wn*t)*np.cos(wd*t - phi)
return x
def derFunc(t, y):
# モデルパラメータ設定
m = cParams["M"]
c = cParams["C"]
k = cParams["K"]
# 状態方程式の立式
u = [y[0], y[1]]
A = [[-c/m, -k/m], [1, 0]]
dy = np.dot(A, u)
return dy
def solverEuler(f, tn, dt, yn):
yn1 = yn + dt*f(tn, yn)
return yn1
def solverRungekutta(f, tn, dt, yn):
k1 = f(tn, yn)
k2 = f(tn+dt/2.0, yn+k1*dt/2.0)
k3 = f(tn+dt/2.0, yn+k2*dt/2.0)
k4 = f(tn+dt, yn+k3*dt)
yn1 = yn + dt*(k1 + 2.0*k2 + 2.0*k3 + k4)/6.0
return yn1
if __name__ == "__main__":
# 変数準備(固定ステップで計算するためあらかじめ用意しておく)
sim_start = cParams["SIM_START"]
sim_end = cParams["SIM_END"]
sim_step = cParams["SIM_STEP"]
num_step = int((sim_end-sim_start)/sim_step) + 1
t = np.linspace(cParams["SIM_START"], cParams["SIM_END"], num_step)
v0 = cParams["V0"]
x0 = cParams["X0"]
# 数値計算の格納結果
v_eu = np.zeros(num_step)
x_eu = np.zeros(num_step)
v_rk = np.zeros(num_step)
x_rk = np.zeros(num_step)
# 解析解の計算
x = calcAnalyticalSolution(t)
# 数値計算による解
for i in range(t.size):
if (i < 1):
# 初期値
[v_eu[i], x_eu[i]] = [v0, x0]
[v_rk[i], x_rk[i]] = [v0, x0]
else:
# 前進オイラー法
[v_eu[i], x_eu[i]] = solverEuler(derFunc,
t[i-1],
sim_step,
[v_eu[i-1], x_eu[i-1]])
# ルンゲクッタ法
[v_rk[i], x_rk[i]] = solverRungekutta(derFunc,
t[i-1],
sim_step,
[v_rk[i-1], x_rk[i-1]])
# グラフ確認
plt.plot(t, x, 'k', lw=3.0, label='Analytical Solution')
plt.plot(t, x_eu, 'g', lw=1.0, label='Euler method')
plt.plot(t, x_rk, 'r--', lw=1.0, label='Runge kutta method')
plt.xlim(0, 3.5)
plt.ylim(-0.04, 0.07)
plt.xlabel('Time (s)')
plt.ylabel('Displacement x(m)')
plt.legend()
plt.grid()
plt.show()
# plt.savefig("./1dofVibSimulation.png")
解析解は関数「calcAnalyticalSolution」で計算している。
オイラー法とルンゲクッタ法による数値計算を実行する関数はそれぞれ「solverEuler」「solverRungekutta」である。当関数は定義された微分関数を引数 f 変数で受取り、各種積分公式をもとに計算を実行する。
微分関数の定義は関数「derFunc」にて行っており、先で準備した状態空間表現の式を定義している。
プログラムの実行結果
実行結果を以下に示す。
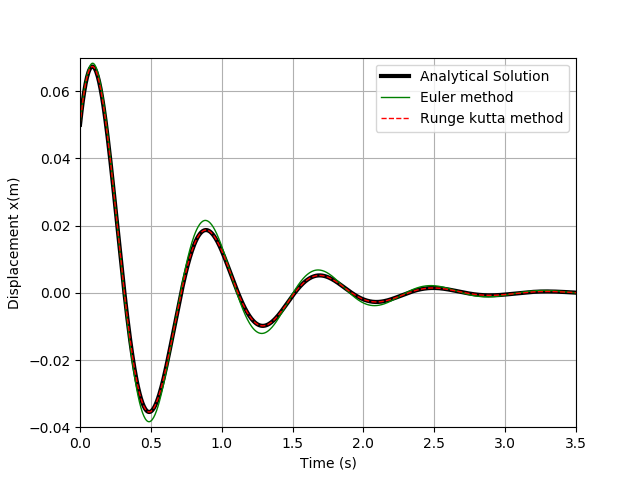
解析解を黒実線、ルンゲクッタ法の数値計算結果を赤点線で示しているがおおよそ解析解と一致している。一方、オイラー法の数値計算結果は緑の実線で示しているが、曲線特性が激しく変化する箇所では精度が落ちていることが分かり、テイラー展開の近似適合の次数の違いが表れていることが確認できる。