pythonで単音の音程を判別する

#動機
私はギターを嗜んでおり、自分の好きな曲に合わせて弾いたりしています。
しかし絶対音感というものは持ち合わせていません。
そこで、音声データからコードを解析するものの作成を目指します。

#概要
まずは、単音が録音されているwavファイルからその単音の音程を特定します。

#関連知識
基本的で上辺を撫でたこと事しか書いていませんが、改めて自分で調べたことをまとめています。

##音について
音とは空気の粗密の振動により発生し、その振動の周波数によって音程というものが定まっている。
同じ音程であっても、楽器、人により音色が違うのは倍音の含まれ方が違うからです。
倍音とは音程（基音）の整数倍の周波数の音ののことです。

ドレミファソラシド(CDEFGAB)といった音階には２種類あります。

音階の各音が協和するように、周波数比が簡単な整数比になるように決めたものが純正律（純正調）音階です。
これに対して、１オクターブ間を周波数比が等しくなるように１２等分したものが平均律音階です。現在のピアノをはじめとする多くの楽器は平均律に従って調律されています。
今回は、平均率(equal temperament)を採用し以下のサイトを参考にしました。

##FFT
まず、フーリエ変換とは信号を連続時間領域から連続周波数領域に変換するものです。
これは、信号にどの周波数の成分がどれほど含まれているかを示すことができます。
上記で述べた通り、音程は周波数によって決定するので、フーリエ変換を行うこで解析ができるようになる。
しかし、デジタル信号は離散的で扱うことができない。

そこで、離散フーリエ変換とは信号を離散時間領域から離散周波数領域に変換するものです。
しかし、このままでは計算時間が大きく現実的ではない。
FFT(Fast Fourier Transform)とは、離散フーリエ変換を高速に行うアルゴリズムです。

PythonではSciPyやNumPyといったライブラリにFFTの関数が用意されている。
今回はNumpyのものを使用する。

#プログラム
今回クラスで作成し、ファイルを与えて処理することで、他の結果と比較しやすいようにした。

ソースコードはGitHubにあります。

##フィールド

    #音名
    vecInterval=[]
    #周波数
    vecFreq=[]
    #周波数：音名
    mapInterval=[]
    #ファイル名
    filename=""
    #生データ
    data=[]
    #サンプリング周期
    rate=0
    #時間軸
    time=[]
    #FFT処理後データ
    fftData=[]
    #周波数リスト
    fftFreq=[]
    

##コンストラクタ

def __init__(self,file):
        #音名マップ
        #音名の配列作成
        self.vecInterval = ["A0","A#0","B0"]
        for i in range(1,8):
            self.vecInterval.append("C" + str(i))
            self.vecInterval.append("C#" + str(i))
            self.vecInterval.append("D" + str(i))
            self.vecInterval.append("D#" + str(i))
            self.vecInterval.append("E" + str(i))
            self.vecInterval.append("F" + str(i))
            self.vecInterval.append("F#" + str(i))
            self.vecInterval.append("G" + str(i))
            self.vecInterval.append("G#" + str(i))
            self.vecInterval.append("A" + str(i))
            self.vecInterval.append("A#" + str(i))
            self.vecInterval.append("B" + str(i))
        self.vecInterval.append("C8")
        #音程の周波数の配列作成
        self.vecFreq.append(27.5)
        semtiones = pow(2,1/12)
        for i in range(0,87):
            self.vecFreq.append(self.vecFreq[i]*semtiones)
        #二つの配列で「周波数:音名」dictを作成
        self.mapInterval = dict(zip(self.vecFreq,self.vecInterval))
        
        #ファイル読み込み
        self.filename = file
        
        #音源読み込み
        self.rate, self.data = scipy.io.wavfile.read(self.filename)
        #横軸（時間）を作成
        self.time = np.arange(0,self.data.shape[0]/self.rate,1/self.rate)    
        
        #FFT
        self.fftData = np.abs(np.fft.rfft(self.data))
        self.fftFreq = np.fft.fftfreq(self.fftData.shape[0],1.0/self.rate)

行っていることは

• 音名の配列、それに対応する周波数の配列、その二つを組み合わせた辞書の作成
• 受け取ったファイル名のファイルを読み込む
• FFTを処理
  です。

##そのままの波形を表示

    def displayFigUneditWav(self):

        #データプロット
        fig = plt.figure()
        ax = fig.add_subplot(111)
        #軸ラベル
        ax.set_xlabel("Time[s]")
        ax.set_ylabel("Amplitude")
        #プロット
        ax.plot(self.time,self.data,label=self.filename)

        plt.legend()
        #グリッド
        plt.grid(axis="both")

        #表示
        plt.show()

横軸が時間、縦軸が振幅の波形を表示する。

##FFTを処理した波形を表示

    def displayFigFFTWav(self,peak):

        #ピーク値を取得
        fft_max_data = signal.argrelmax(self.fftData,order=peak)

        #データプロット
        fig = plt.figure()
        ax = fig.add_subplot(111)
        #軸ラベル
        ax.set_xlabel("Frequency[s]")
        ax.set_ylabel("Gain")
        #プロット
        ax.loglog(self.fftFreq,self.fftData,".-",label=self.filename)
        ax.plot(self.fftFreq[fft_max_data],self.fftData[fft_max_data],"ro",label="peak")
        ax.legend()
        #グリッド
        ax.grid(axis="both")
        #表示
        plt.show()

        #最もゲインの大きいピークの周波数を返す
        maxPeakFreq = self.getPeakFreq(self.fftFreq[fft_max_data],self.fftData[fft_max_data])
        #その周波数に最も近い音名を返す
        intervalName = self.searchInterval(maxPeakFreq)
        return intervalName,self.fftFreq[fft_max_data]

横軸が周波数、縦軸がゲインの波形を表示し、その音程と倍音と思わしき周波数の配列を返す。
peakの値を変更することで、基音、倍音の判定が変わる。
この値を大きくすることで、判定が厳しくなりデータ数が少なくなる。

#結果
音声データは三種類

• 魔王魂のピアノ2-6ラ:https://maou.audio/category/se/se-inst/
• ガレージバンドのピアノのラ
• 自身の声
  で行った。

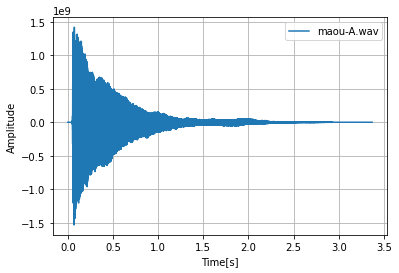
##そのままの波形
maou-A.wav

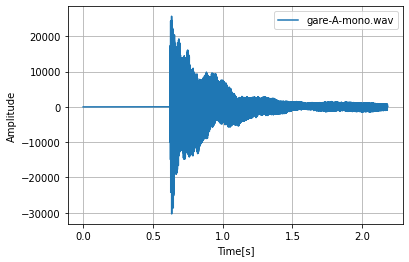
gare-A-mono.wav

koe-A.wav

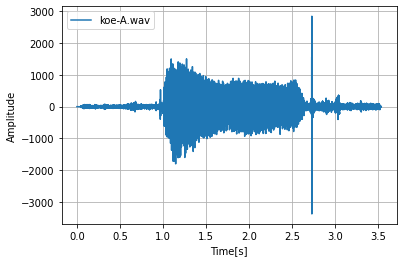
このような結果でした。
maou-Aとgare-A-monoはピアノの音ですが、鳴り始めた時間と大きさが違います。
koe-Aは形から違い、この結果では全て異なった結果が得られました。

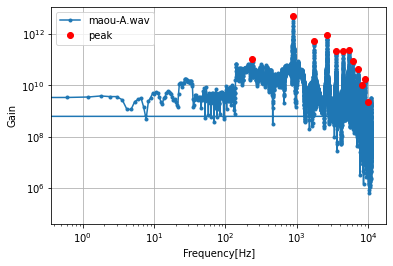
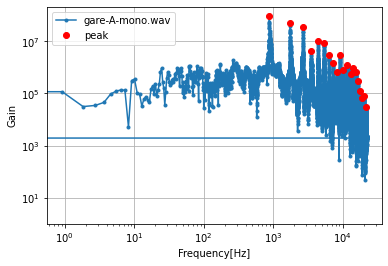
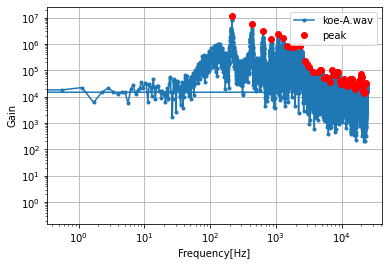
##FFTを行った波形
maou-A.wav

gare-A-mono.wav

koe-A.wav

このような結果でした。

##返ってきた音程と周波数配列
maou-A.wav

maou.Interval
'A5'
maouFreq[1:5]
array([879.55481388, 1759.70311953, 2644.59935941,3533.65004172])

gare-mono.wav

gareInterval
'A5'
gareFreq[0:5]
array([ 879.98337144, 1763.63334026, 2650.03325712, 3542.84971939,
       4443.91602577])

koe-A.wav

koeInterval
'A3'
koeFreq[0:5]
array([ 214.04115633,  428.08231266,  642.12346899,  855.59987293,
       1069.64102926])

この結果から、正確に読み取れている。（koe-A.wavだけA3なのは著者が音痴だからです）
そして、maouFreqとgareFreqを比較すると、基音(879[Hz])から４音を比較すると

-0.4285575627001208
-3.9302207291566447
-5.433897713401166
-9.199677673680526

周波数が高くなるにつれて差も大きくなっている。
おそらくこの差が音色の違いが現れていると思う。

#課題とこれから
単音の判定は可能になったが、連続した単音やコードには対応できていない。
試しにこのプログラムにコードのファイルを処理させてみたが、ゲインのグラフでピークの値がそれほど極端に出ていなかった。
ピークの判断のあたりを改良する必要がありそうです。

今後は、

• 区切って処理することで、長い時間の音声データにも対応
• ブラウザ上でPCのマイクの音などいちいちファイルにしなくてもよい
  このようにしていきたいです。

#感想
作り始めてから
https://play.google.com/store/apps/details?id=jp.co.yamaha.emi.chordtracker&hl=ja&gl=US
完成したものに気づきました。

以前この記事を書いたのですが、企画に乗っかったからこそ読まれたと思いますが、初めて人に自分の文章を読んでもらう喜びを覚えました。
だからこそ、さっそく新たに寄稿したわけですが、モチベーションを上げて自己研鑽を積みたいともいます。
若輩者ですので、詳しい方は是非ご指摘などよろしくお願いいたします。
早速質問というか、変数などの命名はどういった名前が分かりやすいのでしょうか。
英語の知識が乏しいのも相まってわかりにくくてしょうがないと感じます。

また、大学の授業で得た知識をこういった形で体現化することで、より理解が深まると信じて完成させたいと思います。

#参考
matplotlibの使い方
https://docs.scipy.org/doc/scipy/reference/generated/scipy.io.wavfile.read.html
https://qiita.com/HidKamiya/items/c3cc11438d1f67f655cb
https://pystyle.info/matplotlib-set-xy-label-and-title/

音声データの読み込み、fft
https://jorublog.site/python-voice-analysis/
https://101010.fun/programming/python-fft-first-step.html

ノイズ除去
https://momonoki2017.blogspot.com/2018/03/pythonfft-4.html

音の周波数
https://www.petitmonte.com/javascript/musical_scale_frequency.html

音源
https://maou.audio/category/se/se-inst/

ピーク検出
https://qiita.com/yoneda88/items/0cf4a9384c1c2203ea95
https://qiita.com/wrblue_mica34/items/e174a71570abb710dcfb

近い値を取り出す
https://qiita.com/icchi_h/items/fc0df3abb02b51f81657

FFT
https://ari23.hatenablog.com/entry/dsp-frequency-analysis-fft

平均率
http://www.enjoy.ne.jp/~k-ichikawa/junseiritsu2.html