はじめに
大学時代にニューラルネットの重みを遺伝的アルゴリズムで最適化するという手法の研究をしていました。
ニューラルネットのコードはDeepLearningの流行により大量にサンプルがありますが、遺伝的アルゴリズムはあまりないので、過去にC++で作っていたものをPythonに移植してみました。
[2019/7/12] コードをアップしました。
遺伝的アルゴリズムとは
生物の進化を模倣した最適化手法です。
手法にもよりますが、主な流れは以下のようになります。
- 複数の個体で構成された集団を作成する。(1つの個体は複数の染色体を持つ。1つの染色体は複数の遺伝子を持つ。(染色体に関しては記載していない参考書もあります。))
- 任意の評価方法により評価し、各個体の適合度を求める。
- 集団から任意の個体を選択(選択された個体を親と呼ぶ)し、交叉、淘汰により、子を複数個生成する。
- 生成した子を評価する。
- 親と子の中から適合度に基づき選択し、集団と入れ替える(世代交代)。
- 3.~5.を最大世代数まで繰り返す。
遺伝子はビット列で表現しているものが基本ですが、実数で表現したものが実数値遺伝的アルゴリズム(以下、「実数値GA」)です。ニューラルネットワークの重みは実数なので、重みの最適化に実数値GAが使用できます。
実数値GAに関しては、以下の説明が分かりやすいです。
実数値遺伝的アルゴリズムざっくり説明
実数値GAの手法に関して
実数値GAの手法は、主に世代交代モデルと交叉法に分かれます。
- 世代交代モデル(子と親の入れ替えルール):MGG、JGGなど
- 交叉法(親から子を作る手法):BLX-α、UNDX、REXなど
今回は以下の手法を用いました。
- 世代交代モデル:MGG
- 世代交代数:2個体(エリート選択:1個体、ルーレット選択:1個体)
- 致死個体(任意のパラメータが探索範囲を超えた個体) への対応:探索範囲を超えたパラメータを限界値に設定する
- 交叉法:BLX-α (α=0.5)
実装
githubに置いています。
https://github.com/SwitchBladeJW/RCGA
評価方法
最適化アルゴリズムを評価するためのベンチマーク関数を用いて評価しました。
様々なベンチマーク関数に関しては、以下に詳しく記載があります。
[最適化アルゴリズムを評価するベンチマーク関数まとめ]
(https://qiita.com/tomitomi3/items/d4318bf7afbc1c835dda)
今回は、Rastrigin関数、Schwefel関数、RosenBrock関数を用いました。最適化対象のパラメータは、x[i]で表しています。パラメータ数(次元数)が増えるほど難易度があがります。
Rastrigin関数
- 多峰性関数
- 探索範囲:-5.12~5.12
- 大域的最適解 : = 0 , (x[i] = 0)
- 2次元のグラフ
関数の実装
def OriginalRastrigin(x , n):
value = 0
for i in range(n):
value += x[i]**2 - 10 * np.cos(2 * np.pi * x[i])
value += 10 * n;
return value
2次元
- 最大世代数:300世代
- 集団数:50個体
- 生成子個体数: 200個体/世代
- 初期集団の分布:-5.12~-2.0(次元数が少ないので、最適解を外して分布させています)
X軸に世代数、Y軸に適合度(ベンチマーク関数の出力値)を示しています。
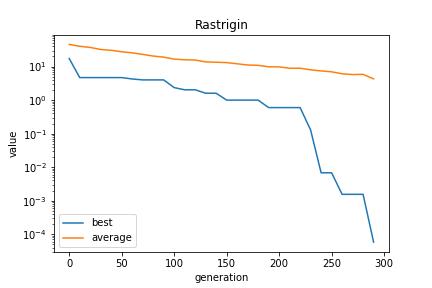
最良個体の適合度は、ほぼ0になっています。
個体の分布を10世代毎に表示しています。赤のプロットが最良個体です。
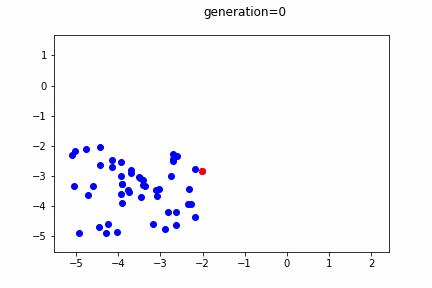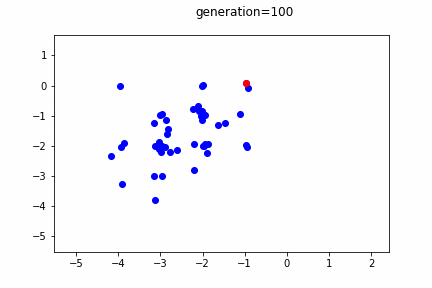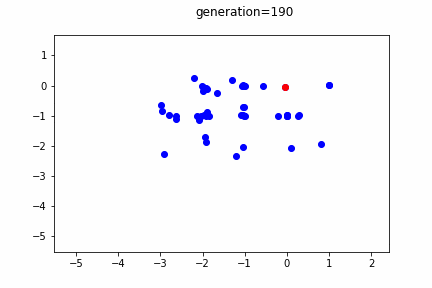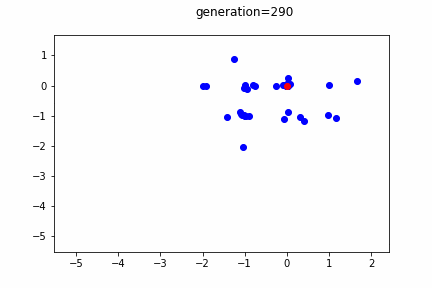
世代が進むごとに、最良個体・全体的な個体の分布ともに、解であるx[i] = 0に近づいていることが分かります。
しかしながら、突発的に離れた位置出現する個体も出現します。この突発的な個体の発生により、局所解に安直に収束してしまうことを抑止しています。
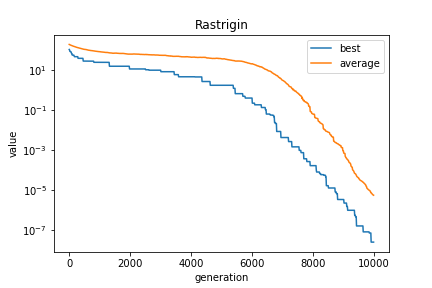
10次元
- 最大世代数:10000世代
- 集団数:300個体
- 生成子個体数: 200個体/世代
- 最良個体の適合度:2.6041760747830267e-08
- 最良個体のパラメータ:[-3.4247764461144783e-06, -3.50417428178406e-06, -2.2482164776969737e-06, -3.4710844379463296e-06, 7.737721637384039e-06, 2.005039335095373e-06, 1.4943778912332043e-06, 1.1181528330355657e-06, -1.3276047526638224e-06, 4.584145661221937e-06]
最良個体の適合度・各パラメータとも、ほぼ0になっていて、大域的最適解を求めることに成功しています。
Schwefel関数
- 多峰性関数
- 探索範囲:-512~512
- 大域的最適解 : ≒0 、(x[i] = 420.9687)
- 2次元のグラフ
関数の実装
def Schwefel(x , n):
value = 0
for i in range(n):
value += x[i] * np.sin(np.sqrt( np.absolute(x[i])))
value = 418.9828873 * n -value
return value
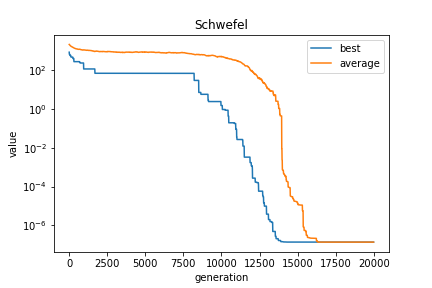
5次元
- 最大世代数:20000世代
- 集団数:300個体
- 生成子個体数: 200個体/世代
- 最良個体の適合度:1.3783119356958196e-07
- 最良個体のパラメータ:[420.96874642945215, 420.96874622367926, 420.9687463066047, 420.9687462407308, 420.96874637971456]
最良個体の適合度は0、各パラメータは420.9687になっており、大域的最適解を求めることに成功しています。
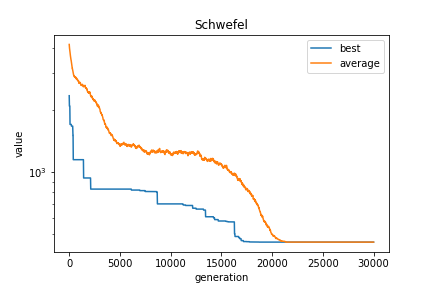
10次元
- 最大世代数:30000世代
- 集団数:300個体
- 生成子個体数: 200個体/世代
- 最良個体の適合度:459.013618910642
- 最良個体のパラメータ:[-512.0, -512.0, -512.0, 420.96874590356066, 420.9687464738711, 420.96874601955557, 420.96874651347804, 420.96874593930437, -512.0, 420.9687465753185]
最良個体の適合度は0になっておらず、各パラメータも-512のものが含まれています。
また、グラフ上で最良個体の適合度と平均値がほぼ同じになってから、数世代変化がないことから、局所解にはまっていると考えられます。
これは、交叉法を変更することにより、改善される可能性はあります。(UNDXであれば、20次元くらいまではいけたはず。)
RosenBrock関数
- 単峰性関数
- 探索範囲:-2.048~2.048
- 大域的最適解 : =0 、(x[i] = 1)
- 2次元のグラフ
関数の実装
def Rosenbrock(x , n):
value = 0
data0 = x[0]
for i in range(1,n):
value += (100 * (( x[i]- data0**2)**2) + (data0 -1)**2) ;
data0 = x[i]
return value
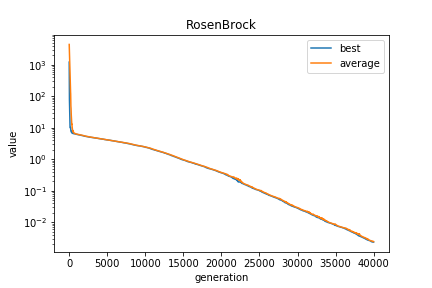
10次元
- 最大世代数:40000世代
- 集団数:50個体
- 生成子個体数: 200個体/世代
- 最良個体の適合度:0.00231321972664098
- 最良個体のパラメータ:[0.9997860990802784, 0.9995464743876002, 0.999245405812484, 0.9985238486102694, 0.9972306954418255, 0.9944574214248189, 0.9892222116196303, 0.9794177542383247, 0.9596324800238759, 0.9207654458523167]
ほぼゼロになっていますが、グラフ上では最良個体の適合度、平均値ともまだ下がっているので、最大世代数を増やすとさらに0に近づく可能性があります。
今後やること
-実装の整理
-UNDXの実装
-ニューラルネットの重み最適化に適用(できれば、TensorFlowを使って)