はじめに
ここ数年DeepLearningといった機械学習が流行っています。
んが、機械学習の仲間1である遺伝的アルゴリズム(Genetic Algorithm:GA)に関してはそこまで記事がありません。また学生の時に研究していた実数値遺伝的アルゴリズム(実数値GA)についてはさらに記事が少なく悔しいので説明等々を書きたいと思います。
最適化問題を解く様な時に参考になれば。2
実装に関してはこちらに書きました。
注意
- 正式な単語を使っていない箇所もありますが、ざっくり説明ということでご了承ください。
- 私個人のイメージも多分に入っているので、正確に知りたい方はググって下さいませ
想定読者
- 遺伝的アルゴリズムについて簡単なイメージがある
- 最適化問題に興味がないこともない
遺伝的アルゴリズムとは
実数値GAの説明の前に遺伝的アルゴリズムを簡単に説明します。
遺伝的アルゴリズムとは、生物の進化(自然淘汰)を模した最適化アルゴリズムの一つです。
ある条件(=評価関数)に適した値の組み合わせを探索するため、解の候補を遺伝子として表現し、以下の手順を繰り返て遺伝子を変化させながら最適な値を探索します。
- 選択
- ルーレット選択などで個体を選択
- 交叉
- 1点交叉個体などで個体同士の遺伝子を入れ替え新しい個体を作る
- 突然変異
- 値の反転などで個体の遺伝子を変化させる
遺伝子はバイナリ(0/1)など整数列(=解候補)で表現したりします。
選択、交叉、突然変異などこちらの図がわかりやすいかもです。
http://www.sist.ac.jp/~kanakubo/research/evolutionary_computing/ga_operators.html
遺伝的アルゴリズムとニューラルネットの関係
せっかくなので、実数値GAの説明の前に話題となってるニューラルネット(DeepLearning)と遺伝的アルゴリズムの関係をざっくりと。
カテゴリとしては両方とも機械学習という分野のものですが、解として導出する対象が異なります。
- 遺伝的アルゴリズムは、条件に対して最適な解を導出する値の探索を行う
- ニューラルネットは、入力に対して予測(回帰)や分類を行う
以下の式で表現してみます。
y = f(x) \\
上記は$x: 入力$, $y: 出力(解)$, $f(x): xを入力とし、yを出力する関数$を意味しています。
上記の関係に対して、イメージ的にはそれぞれこんな感じです。
- 遺伝的アルゴリズム
- 分かっていること:$関数f(x)$
- 目標:最適な$y$を出力する$入力x$を探索する
- ニューラルネット
- 分かっていること:$x, y$
- 目標:$x, y$を元に、未知の$x'$に対して適した$y'$を出力する$関数f(x)$を生成する
実数値GAとは
実数値GAは、遺伝子の表現を実数とした遺伝的アルゴリズムです。
現実世界では整数値の組み合わせだけでなく、実数値の組み合わせの問題も多いため、遺伝子を実数値で表現する場合に使用されることが想定されます。3
基本的な動作は遺伝的アルゴリズムと同じですが、選択、交叉、突然変異の方法は遺伝子の表現を考慮して変更する必要があります。
これは実数値GAだけでなく、遺伝子の表現によって適切に変更、選択する必要があります。
遺伝子が実数の場合、遺伝子の交換ではなく新たな値を生成するような交叉方法が必要になります。
例えば、実数値GAとして手法の一例を以下に挙げます(別記事にてざっくりですが説明します)。
- 選択
- Minimal Generation Gapなど
- 交叉
- BLX_alphaなど
- 突然変異
- しなくてもよい(交叉に突然変異要素が含まれているとする考えの元)
実数値GAの性能評価
評価関数
実数値GAは、ある条件(評価関数)に対して大域最適解を出力する入力を発見する事が目標になります。
評価関数には大域最適解だけではなく、局所解というものもあるため、正しく大域最適解を出力する入力を探索できるか否かが重要になります。
実数値GAは、作成した実数値GAが正しく大域最適解を探索できるか否か、その性能を評価するためにベンチマーク関数を用いて評価します。
使われるベンチマーク関数の性質として次のようなものが存在します。
- 単峰性関数
- 大域最適解のみしかない関数
- 一般的に多峰性関数に対して最適解の探索は容易
- 多峰性関数
- 大域最適解以外に局所解が存在する関数
- 局所解に陥る可能性があるため、一般的に単峰性関数に対して最適解の探索は困難
単峰性関数のイメージ(最適解は$x=0$)
$f(x)=x^{2}$

多峰性関数のイメージ(最適解は$x=0$)
$f(x) = x^{2}-cos(2 \pi x)$
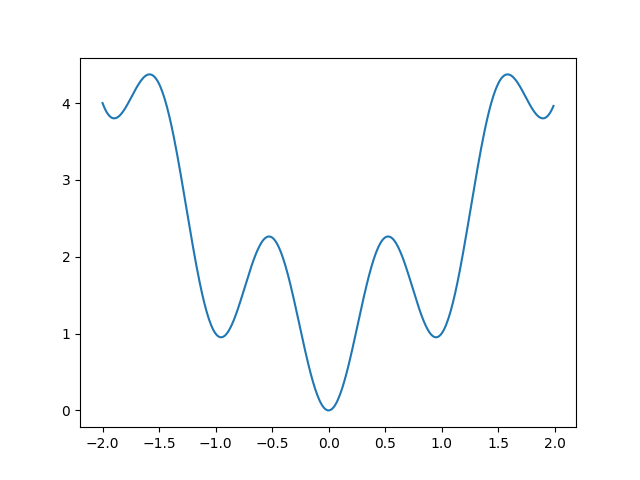
イメージとしては、単峰性関数で収束速度(最適解を探索するまでの速度)、多峰性関数で解の探索性能(複雑な形状でも最適解を探索できる性能)を見る、といった感じかと。
一般的に収束速度と探索性能はトレードオフの関係になります。
その他、ある遺伝子(変数)の値が解に寄与する割合が高い(= 評価関数の形状が複雑)等といった関数も最適解の探索が難しい傾向にあります。
ベンチマーク関数に関しては以下に詳しく纏まっています。
関数の図を見るだけでも探索する空間のイメージがつくと思います。
https://qiita.com/tomitomi3/items/d4318bf7afbc1c835dda
評価回数
遺伝的アルゴリズムは、最適解を発見するまでの時間も評価に入ります。
最適解を発見するのに1日かかるものと5分で終わるもの、どちらが良いか、ということを想像して頂ければイメージがつきやすいでしょうか。
実数値GAでは、生成した遺伝子(実数値の組み合わせ)を評価する(=評価関数を計算する)事に時間がかかるとされています。そのため、いかに評価関数を使わず最適解を発見できるか、という所がアルゴリズムの評価に入ります。4
最後に
実数値GAに関してざっくり説明をしました。
次の記事ではPythonを使った実装コードとその説明をやはりざっくり行いたいと思います。