Euler法（Pythonで数値計算プログラムを書き直そうシリーズ）

Pythonで数値計算プログラムを書き直そうシリーズ
　間違いがあれば教えてください（土下座）
　理論や精度保証云々より、実装メインの話になります。

##はじめに
　常微分方程式の初期値問題の数値解法として、まず有名なのがEuler法です。初期値問題は次のように書きます。

\begin{align}
&\frac{dy}{dt} = f(t,y) \\
&y(t_0) = y_0
\end{align}

　解の計算には、関数$y(t)$の$t_0$周りにおけるテイラー展開を、1次の項までで打ち切った式が使われます。いわゆる前進差分の式で、陽解法とか1次精度の差分スキームとかも言われます。誤差は$O(\Delta t)$なので$\Delta t$に比例します。
$$y(t_0 +\Delta t) = y(t_0) +\frac{dy(t_0)}{\Delta t}\Delta t$$

　要はある時点の$y(t_0)$に対して、変化量$dy = \frac{dy(t)}{\Delta t}\Delta t$をどんどん足せば離れた所の$y(t)$も分かるだろうという、いかにも累積誤差が増えそうな手法です。参考資料のリンクもいくつか貼っておきます。

オイラー法　パソコンで数値計算
【Python】オイラー法のプログラム - アルゴリズム雑記
Python - 微分方程式数値解法 オイラー法 & 中心差分法＆ルンゲクッタ法
[C言語] 1階常微分方程式の解法（オイラー法）
[C言語] 2階常微分方程式の解法（オイラー法）
常微分方程式(初期条件あり)の数値解析による解軌跡の導出
オイラー法/ホイン法/ルンゲクッタ法をつかった常微分方程式の数値解析超入門
ルンゲ-クッタ法の安定性解析

##完成したプログラム

euler.py

#Euler法による常微分方程式の解法プログラム
import numpy as np  #NumPyライブラリ
import matplotlib.pyplot as plt  #データ可視化ライブラリ


#導関数dy/dt
def func_dydt(t, y):
    return t**2.0 -3.0  #dy/dt = t^2 -3.0


#Euler法（導関数、tの初期値、yの初期値、刻み幅dt）
def euler(func_dydt, t, y, dt=1e-3):
    dy = func_dydt(t, y)*dt  #変化量を計算

    t += dt  #変数を更新
    y += dy  #変化量を加えて更新

    return t, y


#常微分方程式を逐次計算（導関数、yの初期値、tの開始点、tの終了点、刻み幅dt）
def ode_calc(func_dydt, y_start, t_start, t_end, dt=1e-2):
    num_calc = 0  #計算回数
    t_div = np.abs((t_end-t_start)/dt)  #格子分割数
    if(t_end<t_start):  #負の方向に計算する時は刻み幅の符号を反転
        dt = -dt

    #初期値
    t = t_start  #独立変数t
    y = y_start  #従属変数y
    print("t = {:.7f},  y = {:.7f}".format(t, y))

    #グラフ用データを追加
    t_list = [t]
    y_list = [y]

    #ずっと繰り返す
    while(True):
        t, y = euler(func_dydt, t, y, dt)
        print("t = {:.7f},  y = {:.7f}".format(t, y))

        #グラフ用データを追加
        t_list.append(t)
        y_list.append(y)

        num_calc += 1  #計算回数を数える

        #「計算回数が格子分割数以上」ならば終了
        if(t_div<=num_calc):
            print("Finished.")
            print()
            break

    return t_list, y_list


#可視化
def visualization(t_list, y_list):
    plt.xlabel("$t$")  #x軸の名前
    plt.ylabel("$y(t)$")  #y軸の名前
    plt.grid()  #点線の目盛りを表示

    plt.plot(t_list,y_list, label="$y(t)$", color='#ff0000')  #折線グラフで表示
    plt.legend(loc='best') #凡例(グラフラベル)を表示
    plt.show()  #グラフを表示


#メイン実行部
if (__name__ == '__main__'):
    #Euler法でdt離れた点の値を取得
    t, y = euler(func_dydt, 0.0, 0.0)
    print("t = {:.7f},  y = {:.7f}".format(t, y))

    #常微分方程式を逐次計算
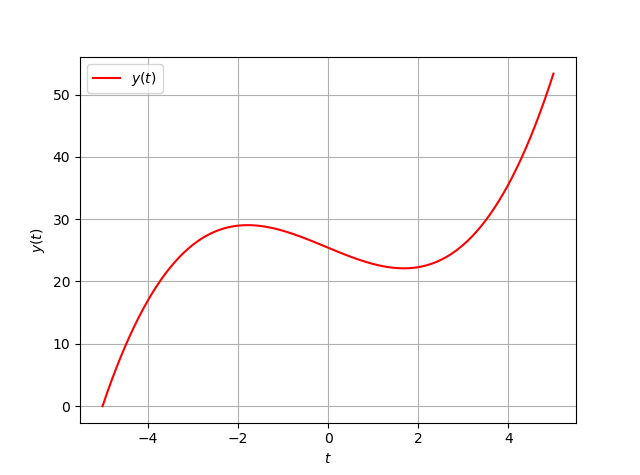
    t_list, y_list = ode_calc(func_dydt, 0.0, -5.0, 5.0)

    #結果を可視化
    visualization(t_list, y_list)

　主なアルゴリズムはeuler関数に書きました。引数として、導関数$\frac{dy}{dt}$、従属変数$y$の初期値、独立変数$t$の開始点、$t$の終了点、刻み幅$dt$を渡すと、計算された$t$と$y$のリストが返ってきます。例として、常微分方程式の初期値問題$\frac{dy}{dt}=t^2-3, y(-5)=0$の解を求めています。プログラムは地味ながら、$f(t,y)$が$t$の関数でも$y$の関数でも対応できるようにしていたり、（終了点）＜（開始点）となっていれば負の方向にも計算できるようにしてあります。
　個人的にモジュールとして呼び出し可能にしたかったので、そういう構造になっています。モジュールとして使うテストプログラムは以下に書きました。この例では、$\frac{dy}{dt} = cost, y(5)=0$と、$\frac{dy}{dt}=-y(t), y(0)=5$の解を求めます。

euler_test.py

import numpy as np  #数値計算用モジュール
import euler


def func_dydt1(t, y):
    return np.cos(t)  #dy/dt = cos(t)

t_list1, y_list1 = euler.ode_calc(func_dydt1, 0.0, 5.0, -5.0, dt=1e-1)
euler.visualization(t_list1, y_list1)


def func_dydt2(t, y):
    return -y  #dy/dt = -y(t)

t_list2, y_list2 = euler.ode_calc(func_dydt2, 5.0, 0.0, 10.0)
euler.visualization(t_list2, y_list2)

##注意すべきと思う点
　細かい話が多いですが、ちょっとの工夫でこういうことができるのに、という内容を羅列します。

###関数項は独立変数も従属変数も含むことがある
　常微分方程式では当然、関数項$f(t,y)$は独立変数$t$の関数のこともあれば、従属変数$y$の関数のこともあります。しかし、書籍やネットでEuler法のプログラムをを探すと、片方の関数しか扱っていないことが多いように思われます。その関係で同じEuler法なのに、情報元によって差分スキームの書き方が違うことがあり、かつての自分は混乱したことがありました。今回のプログラムでは、素直にfunc_dydt関数を作り、$t$の関数でも$y$の関数でも対応できるようにしました。

###独立変数が負の方向にも計算できる
　書籍やネットで情報を探すと、$t$を時間の変数などと考えて、$+t$方向にしか計算していないプログラムが多いように思われます。しかし、元のテイラー展開を考えれば$-t$方向も簡単に計算できるし、tを位置の変数などと考えれば負の方向に計算しても問題ありません。当たり前すぎて説明しないだけかもしれないですが、実装例は意外と見かけませんでした。今回のプログラムでは、負の方向にも計算できるようにしました。

###反復計算の終了条件には工夫の余地がある
　今回のプログラムでは、$t$の開始点と終了点を引数に渡し、$t$が終了点に達したらプログラムを止めるという発想で書きました。しかし、問題によっては$y$の終了点を定義し、終了条件とした方が自然な場合もあります。例えば、物体の自由落下のシミュレーションでは、高さが0になったら（地上に達したら）計算を止める方が都合がいいでしょう。今回は特にその点を考慮していませんが、希望の結果を得るには終了条件の書き換えが必要かもしれません。

###テイラー展開からはn次精度の前進差分スキームを導出できる
　Euler法による精度は1次精度、ルンゲ・クッタ法（ホイン法・中点法）は2次精度という説明をしばしばされます。しかし、前進差分自体は2次精度や3次精度の式も考えることができます。すべてテイラー展開の式から導出できますが、式だけ書くと次のようになります（ただ使い方がよく分からない）。
$$\frac{d y_i}{d x} = \frac{-y_{i+2} +4y_{i+1} -3y_i}{2\Delta x} +O(\Delta x^2)$$
$$\frac{d y_i}{d x} = \frac{2y_{i+3} -9y_{i+2} +18y_{i+1} -11y_i}{6\Delta x} +O(\Delta x^3)$$

##自作プログラムは使えるのか
　PythonでEuler法を扱うモジュールが無いかと探してみましたが、単純なのはNumPyのdiffで差分を取る方法だと思います。また、SciPyであればscipy.integrate.odeintというモジュールがあり、運動方程式やローレンツ方程式も解く例が見つかりました。結構便利そうですが扱い方に癖があったので、別記事にして書きました。

scipy.integrate.odeintの使い方まとめ

　とは言え、細かいことをやろうとすると、結局は自分でプログラムを組んだ方がいいかもしれません。精度を気にしなければ、今回のプログラムでも使えなくはないと思います。