Pythonで数値計算プログラムを書き直そうシリーズの番外編です。少し前にEuler法の記事を書いて以来、常微分方程式の手頃なソルバーが無いか探していたのですが、scipy.integrate.odeintが色々できそうだったのでメモしておきます。
現状の自分の理解としては、「連立常微分方程式を解ける」のがこのソルバーの長所だと思っています。というのも、連立常微分方程式が解けると、高階常微分方程式も式変形することで解けるという利点があるからです。
ただし、scipy.integrateのリファレンスまで辿ってみると、「odeintはFortranで実装された古いソルバー(大部分はODEPACK)で、そのインタフェースは特に便利ではなく、新しいAPIに比べて機能が欠ける」という旨が書かれています。信頼性という意味では歴史のあるODEPACKに利点がある気もしますが、扱いやすさでは初期値問題(initial value problem, IVP)のソルバーであるscipy.integrate.solve_ivpなども検討すべきかもしれません。
odeintの関連情報は、先にいくつか載せておきます。
Python NumPy SciPy : 1階常微分方程式の解法 - Lorenz方程式、内部構造も説明あり
scipyで2階常微分方程式の数値解を求める - 運動方程式
SciPyで常微分方程式の数値解を得る - 井戸型ポテンシャルでの運動方程式
Scipyのodeint,odeで常微分方程式の数値解析 - odeintとodeを使った計算例
Pythonでカオス・フラクタルを見よう! - 3体問題を解いている。でも解析力学わからん。
Pythonを使った数値計算のコツ - 高速化の文脈でodeintを紹介。
微分や微分方程式をPythonで理解する - 主にSymPyを使っている。こっちもアリかも?
1階常微分方程式(1次反応、放射性崩壊、ロジスティック方程式)
とりあえず、単純な常微分方程式を解いてみます。
\frac{dy}{dt} = ay
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
#1階常微分方程式(1次反応、放射性崩壊、ロジスティック方程式)
def func_dydt(y, t):
dydt = a*y
return dydt
#2d可視化
def plot2d(t_list, y_list, t_label, y_label):
plt.xlabel(t_label) #x軸の名前
plt.ylabel(y_label) #y軸の名前
plt.grid() #点線の目盛りを表示
plt.plot(t_list, y_list)
plt.show()
#メイン実行部
if (__name__ == '__main__'):
#常微分方程式(放射性崩壊)
t_list = np.linspace(0.0, 10.0, 1000)
a = -1
y_init = 1.0 #初期値
y_list = odeint(func_dydt, y_init, t_list)
print(y_list)
#可視化
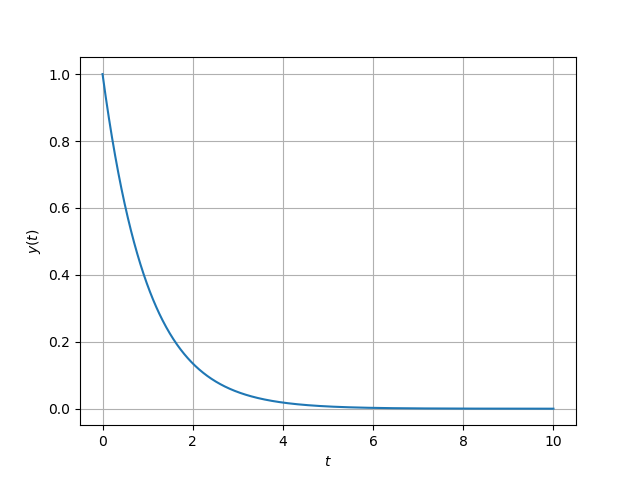
plot2d(t_list, y_list[:, 0], "$t$", "$y(t)$")
結果を見ると、化学物質などが指数的に減少してそうなグラフになっています。
1階連立常微分方程式(Lorenz方程式)
次に、連立常微分方程式の一種である、Lorenz方程式を解いてみます。
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{dx}{dt} = -px +py
\\
\frac{dy}{dt} = -xz +rx -y
\\
\frac{dz}{dt} = xy -bz
\end{array}
\right.
\end{eqnarray}
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#1階連立常微分方程式(Lorenz方程式)
def func_lorenz(var, t, p, r, b):
dxdt = -p*var[0] +p*var[1]
dydt = -var[0]*var[2] +r*var[0] -var[1]
dzdt = var[0]*var[1] -b*var[2]
return [dxdt, dydt, dzdt]
#3d可視化
def plot3d(t_list, var_list):
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_xlabel("$x$") #x軸の名前
ax.set_ylabel("$y$") #y軸の名前
ax.set_zlabel("$z$") #z軸の名前
ax.plot(var_list[:, 0], var_list[:, 1], var_list[:, 2])
plt.show()
#メイン実行部
if (__name__ == '__main__'):
#1階連立常微分方程式(Lorenz方程式)
t_list = np.linspace(0.0, 100.0, 10000)
p = 10
r = 28
b = 8/3
var_init = [0.1, 0.1, 0.1] #3次元座標上での初期値
var_list = odeint(func_lorenz, var_init, t_list, args=(p, r, b))
print(var_list)
#可視化
plot3d(t_list, var_list)
結果を見ると、ローレンツ・アトラクタしてそうなグラフになっています。
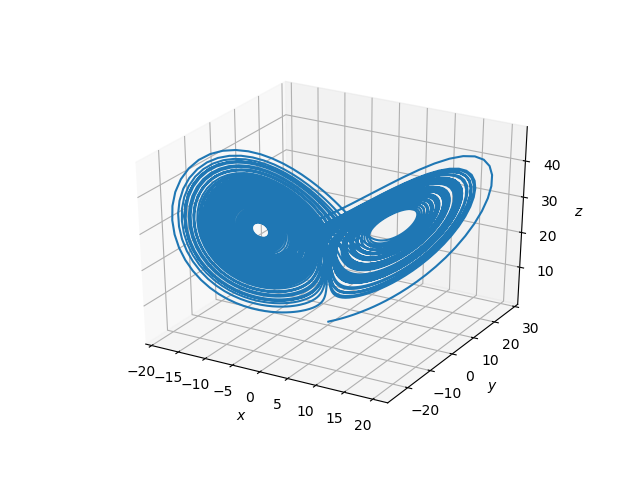
ただし、カオス現象の数値計算は、初期値だけでなく刻み幅の影響も受けるようで、注意点が色々ありそうです。
許容誤差を変えると値が一致しました。ルドルフさんに教えて頂きました。ただこれが何の許容誤差なのかは理解できていません。
— ceptree@モゥフ モゥフ モゥフ モゥフ (@ceptree) April 4, 2018
y = odeint(Lorenz,[x0,y0,z0])
↓
y = odeint(Lorenz,[x0,y0,z0],t,atol=1e-12,rtol=1e-12)https://t.co/0LgJ5U5y8t pic.twitter.com/vVXUbOtoF3
2階常微分方程式(運動方程式、自由落下)
続いて、2階常微分方程式の一種である、運動方程式を解いてみます。
\frac{d^2 x}{dt^2} = -g
このような高階常微分方程式の場合は、1階連立常微分方程式に置きかえることで計算できます。上の運動方程式に対しては、$\frac{dx}{dt} = v$という置換を行います。
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{dx}{dt} = v
\\
\frac{dv}{dt} = -g
\end{array}
\right.
\end{eqnarray}
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
#2階常微分方程式(運動方程式、自由落下)
def func_motion(var, t):
dxdt = var[1]
dvdt = -gravity
return [dxdt, dvdt]
#2d可視化
def plot2d(t_list, y_list, t_label, y_label):
plt.xlabel(t_label) #x軸の名前
plt.ylabel(y_label) #y軸の名前
plt.grid() #点線の目盛りを表示
plt.plot(t_list, y_list)
plt.show()
#メイン実行部
if (__name__ == '__main__'):
#2階常微分方程式(運動方程式、自由落下)
t_list = np.linspace(0.0, 10.0, 1000)
v0 = 0.0 #初速度
gravity = 9.80665 #重力加速度
m_init = [100.0, 0.0] #高さと速度の初期値
m_list = odeint(func_motion, m_init, t_list)
print(m_list)
#可視化
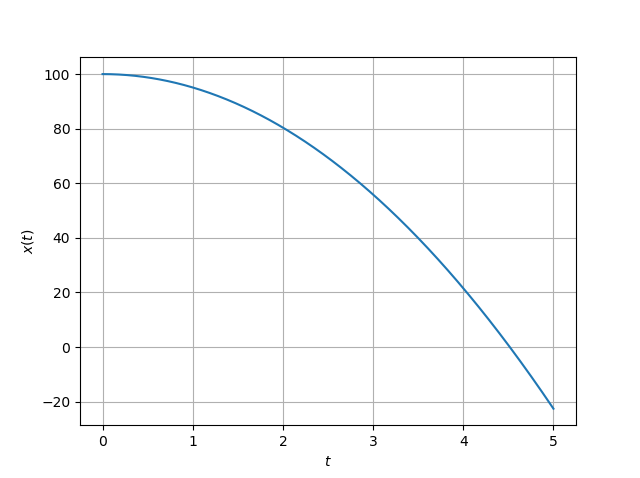
plot2d(t_list, m_list[:, 0], "$t$", "$x(t)$")
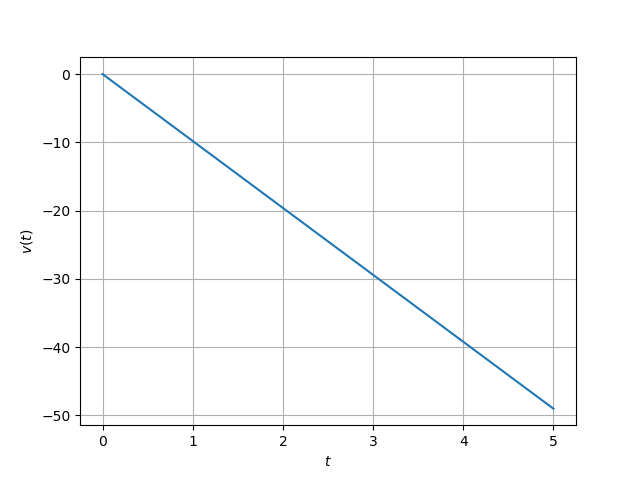
plot2d(t_list, m_list[:, 1], "$t$", "$v(t)$")
結果を見ると、2次関数的に位置が変化してるグラフと、1次関数的に速度が減少してるグラフになっています。
おまけ:多体問題
多体問題を計算している例も見つかりました。関数の定義方法が独特ですが、興味ある方はどうぞ。自分の気が向いたらまた、簡略化したプログラムを追記します(リンク先のプログラムの理屈はよく分かってないので、編集リクエストなどお待ちしてます)。
Pythonでカオス・フラクタルを見よう!
Modelling the Three Body Problem in Classical Mechanics using Python