微分や微分方程式をPythonで理解する

微分や微分方程式は、Sympy というライブラリを使うのが非常に便利です。Scipy もよく使われると思うけど、ちょっと使い方が難しい。

Sympy を使った方法

import sympy as sym
from sympy.plotting import plot
sym.init_printing(use_unicode=True)
%matplotlib inline

指定した文字をシンボル（変数を表す文字）として扱います。

a, b, c, x, y = sym.symbols("a b c x y")

１個１個指定するときは次のような構文も可能です。

a = sym.Symbol('a')

指定した文字を関数として扱います。

f = sym.Function('f')
g = sym.Function('g')

Sympy を使って数学の復習

# 数式は英語で numerial expression または numerical formula
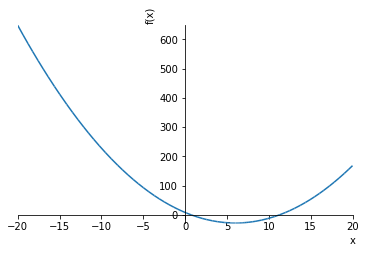
expr = x**2-12*x+8
expr

$$x^{2} - 12 x + 8$$

どんな形の関数か確認したければこう。

# 得られた関数を図示
plot(expr, (x, -20, 20))

# 等式は英語で equation または equality
eq = sym.Eq(expr)
eq

$$x^{2} - 12 x + 8 = 0$$

# このように右辺を明記しても良い
eq = sym.Eq(x**2-12*x, -8)
eq

$$x^{2} - 12 x = -8$$

# 方程式を解く
sym.solve(eq)

$$\left [ - 2 \sqrt{7} + 6, \quad 2 \sqrt{7} + 6\right ]$$

# 代数を使った式も取り扱える
eq = sym.Eq(a * x ** 2 + b * x + c)
eq

$$a x^{2} + b x + c = 0$$

# xについて解く
sym.solve(eq, x)

$$\left [ \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a}, \quad - \frac{b + \sqrt{- 4 a c + b^{2}}}{2 a}\right ]$$

# 因数分解
expr = x**2 + 2*x + 1
sym.factor(expr)

$$\left(x + 1\right)^{2}$$

# 連立方程式
eq1 = 3 * x + 5 * y - 29
eq2 = x + y - 7

sym.solve([eq1, eq2])

$$x : 3, y : 4$$

微分

expr = 2 * x ** 2 + 5 * x - 3
expr

$$2 x^{2} + 5 x - 3$$

# 微分
sym.Derivative(expr)

$$\frac{d}{d x} \left(2 x^{2} + 5 x - 3\right)$$

# 微分を計算する
sym.Derivative(expr).doit()

$$4 x + 5$$

# このように書いても同じ
sym.diff(expr)

$$4 x + 5$$

# sym.Eq を使って等式として表記
sym.Eq(sym.Derivative(expr), sym.diff(expr))

$$\frac{d}{d x} \left(2 x^{2} + 5 x - 3\right) = 4 x + 5$$

# 上と同じ意味だが、変数が１つだけなら上のように省略できる。
# 変数が２つ以上の場合は何で微分するか明記しなければいけない
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{d}{d x} \left(2 x^{2} + 5 x - 3\right) = 4 x + 5$$

# ２階微分
sym.Eq(sym.Derivative(expr, x, 2), sym.diff(expr, x, 2))

$$\frac{d^{2}}{d x^{2}} \left(2 x^{2} + 5 x - 3\right) = 4$$

# xについて微分して x=1を代入
sym.diff(expr).subs(x, 1)

$$9$$

# x について微分
expr = a * x ** 2 + b * x * y + c * y ** 2
sym.diff(expr, x)

$$2 a x + b y$$

# xについて微分して x=1を代入
sym.diff(expr, x).subs(x, 1)

$$2 a + b y$$

いろんな微分の公式

expr = x ** a
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{\partial}{\partial x} x^{a} = \frac{a x^{a}}{x}$$

expr = sym.sin(x)
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{d}{d x} \sin{\left (x \right )} = \cos{\left (x \right )}$$

expr = sym.cos(x)
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{d}{d x} \cos{\left (x \right )} = - \sin{\left (x \right )}$$

expr = sym.exp(x)
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{d}{d x} e^{x} = e^{x}$$

expr = a**x
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{\partial}{\partial x} a^{x} = a^{x} \log{\left (a \right )}$$

expr = sym.log(x)
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{d}{d x} \log{\left (x \right )} = \frac{1}{x}$$

expr = sym.sqrt(x)
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{d}{d x} \sqrt{x} = \frac{1}{2 \sqrt{x}}$$

expr = sym.tan(x)
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{d}{d x} \tan{\left (x \right )} = \tan^{2}{\left (x \right )} + 1$$

expr = sym.sin(x)**a
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{\partial}{\partial x} \sin^{a}{\left (x \right )} = \frac{a \sin^{a}{\left (x \right )} \cos{\left (x \right )}}{\sin{\left (x \right )}}$$

expr = sym.cos(x)**a
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{\partial}{\partial x} \cos^{a}{\left (x \right )} = - \frac{a \sin{\left (x \right )} \cos^{a}{\left (x \right )}}{\cos{\left (x \right )}}$$

expr = sym.tan(x)**a
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{\partial}{\partial x} \tan^{a}{\left (x \right )} = \frac{a \left(\tan^{2}{\left (x \right )} + 1\right) \tan^{a}{\left (x \right )}}{\tan{\left (x \right )}}$$

expr = sym.log(x)**a
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{\partial}{\partial x} \log{\left (x \right )}^{a} = \frac{a \log{\left (x \right )}^{a}}{x \log{\left (x \right )}}$$

expr = f(x) * g(x)
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{d}{d x} f{\left (x \right )} g{\left (x \right )} = f{\left (x \right )} \frac{d}{d x} g{\left (x \right )} + g{\left (x \right )} \frac{d}{d x} f{\left (x \right )}$$

expr = f(x) / g(x)
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))

$$\frac{d}{d x} \frac{f{\left (x \right )}}{g{\left (x \right )}} = - \frac{f{\left (x \right )} \frac{d}{d x} g{\left (x \right )}}{g^{2}{\left (x \right )}} + \frac{\frac{d}{d x} f{\left (x \right )}}{g{\left (x \right )}}$$

常微分方程式

2 f'(x) + 5 f(x) = 0 を解く

# 常微分方程式
eq = sym.Eq(2 * f(x).diff(x,1) + 5 * f(x))
eq

$$5 f{\left (x \right )} + 2 \frac{d}{d x} f{\left (x \right )} = 0$$

# 一般解
ans = sym.dsolve(eq)
print(ans)
ans

Eq(f(x), C1*exp(-5*x/2))

$$f{\left (x \right )} = C_{1} e^{- \frac{5 x}{2}}$$

# 特殊解
ans = sym.dsolve(eq, ics={f(0):1})
print(ans)
ans

Eq(f(x), exp(-5*x/2))

$$f{\left (x \right )} = e^{- \frac{5 x}{2}}$$

plot(ans.rhs, (x, -10, 10)) # rhs は右辺(Right-hand side)の意味

# 特殊解で x = 2 のとき
print(ans.subs(x, 2))
ans.subs(x, 2)

Eq(f(2), exp(-5))

$$f{\left (2 \right )} = e^{-5}$$

Sympy ではこれ以上展開してくれる（小数表示にしてくれる）方法が見つからなかったので、とりあえず numpyなどから関数を借りてきて次のように計算してみました。

# 小数表示
from numpy import sqrt, sin, cos, tan, log, exp
exp(-5)

$$0.006737946999085467$$

f''(x) + f'(x) + 4 f(x) = 0 を解く

# 常微分方程式
eq = sym.Eq(f(x).diff(x,2) + f(x).diff(x,1) + 4 * f(x))
eq

$$4 f{\left (x \right )} + \frac{d}{d x} f{\left (x \right )} + \frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$

# 一般解
ans = sym.dsolve(eq)
print(ans)
ans

Eq(f(x), (C1*sin(sqrt(15)*x/2) + C2*cos(sqrt(15)*x/2))/sqrt(exp(x)))

$$f{\left (x \right )} = \frac{C_{1} \sin{\left (\frac{\sqrt{15} x}{2} \right )} + C_{2} \cos{\left (\frac{\sqrt{15} x}{2} \right )}}{\sqrt{e^{x}}}$$

# 特殊解
ans = sym.dsolve(eq, ics={f(0):1, f(x).diff(x,1).subs(x, 0):1})
print(ans)
ans

Eq(f(x), (sqrt(15)*sin(sqrt(15)*x/2)/5 + cos(sqrt(15)*x/2))/sqrt(exp(x)))

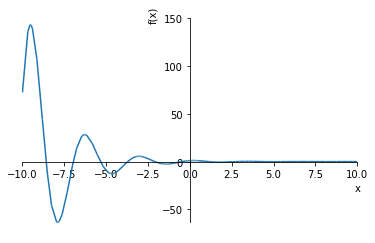
$$f{\left (x \right )} = \frac{\frac{\sqrt{15} \sin{\left (\frac{\sqrt{15} x}{2} \right )}}{5} + \cos{\left (\frac{\sqrt{15} x}{2} \right )}}{\sqrt{e^{x}}}$$

plot(ans.rhs, (x, -10, 10)) # rhs は右辺(Right-hand side)の意味

# 特殊解に x = 2 を代入
ans2 = ans.subs(x, 2)
print(ans2)
ans2

Eq(f(2), (cos(sqrt(15)) + sqrt(15)*sin(sqrt(15))/5)*exp(-1))

$$f{\left (2 \right )} = \frac{\cos{\left (\sqrt{15} \right )} + \frac{\sqrt{15} \sin{\left (\sqrt{15} \right )}}{5}}{e}$$

# 小数表示
from numpy import sqrt, sin, cos, tan, log, exp
(cos(sqrt(15)) + sqrt(15)*sin(sqrt(15))/5)*exp(-1)

$$-0.4641179871879223$$

f'(x) + 0.2 f(x) = 0 を解く, ただし f(0) = 5

eq = sym.Eq(f(x).diff(x,1) + 0.2 * f(x))
ans = sym.dsolve(eq, ics={f(0):5})
print(ans)
ans

Eq(f(x), 5*exp(-0.2*x))

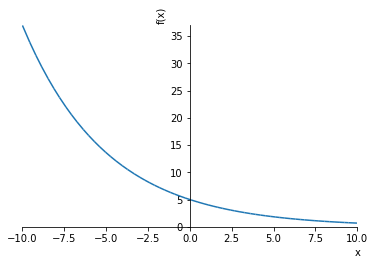
$$f{\left (x \right )} = 5 e^{- 0.2 x}$$

plot(ans.rhs, (x, -10, 10)) # rhs は右辺(Right-hand side)の意味

f'(x) + 0.2 x = 0 を解く, ただし f(0) = 5

eq = sym.Eq(f(x).diff(x,1) + 0.2 * x)
ans = sym.dsolve(eq, ics={f(0):5})
print(ans)
ans

Eq(f(x), -0.1*x**2 + 5)

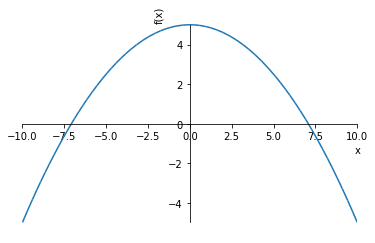
$$f{\left (x \right )} = - 0.1 x^{2} + 5$$

plot(ans.rhs, (x, -10, 10)) # rhs は右辺(Right-hand side)の意味

f'(x) + f(x)/x - 2 を解く, ただし f(1) = 2

eq = sym.Eq(f(x).diff(x,1) + f(x)/x - 2)
ans = sym.dsolve(eq, ics={f(1):2})
print(ans)
ans

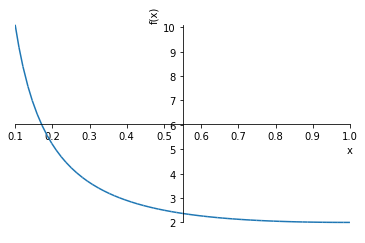
Eq(f(x), x + 1/x)

$$f{\left (x \right )} = x + \frac{1}{x}$$

plot(ans.rhs, (x, 0.1, 1)) # rhs は右辺(Right-hand side)の意味

Scipy.integrate.odeint を使う方法

インターネットで検索すると使用例がいくつか見つかります。たとえば：
https://apmonitor.com/pdc/index.php/Main/SolveDifferentialEquations

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
%matplotlib inline

# function that returns dy/dt
def model(y,t,k):
    dydt = -k * y
    return dydt

# initial condition
y0 = 5

# time points
t = np.linspace(0,20)

# solve ODEs
k = 0.1
y1 = odeint(model,y0,t,args=(k,))
k = 0.2
y2 = odeint(model,y0,t,args=(k,))
k = 0.5
y3 = odeint(model,y0,t,args=(k,))

# plot results
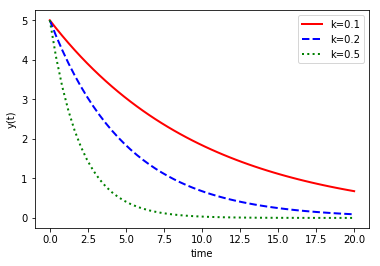
plt.plot(t,y1,'r-',linewidth=2,label='k=0.1')
plt.plot(t,y2,'b--',linewidth=2,label='k=0.2')
plt.plot(t,y3,'g:',linewidth=2,label='k=0.5')
plt.xlabel('time')
plt.ylabel('y(t)')
plt.legend()
plt.show()

微分方程式の数値解法

主なものに Euler法と Runge-Kutta法があります。

課題

以前から何度も申し上げていることですが、便利なツールはどんどん使ってください。使い方に習熟してください。しかし、その原理を理解しておくことも同じく重要です。今回も、前回と同様に、上記の便利なツールの使い方を知った上で、動作原理を勉強する（そしてPythonの勉強をする）ために以下の課題にチャレンジしてください。

• Euler法とRunge-Kutta法の違いについて、インターネットで調べて説明してください。

• x₀ = 1 で y₀ = 2 となる初期条件で微分方程式 dy/dx = 2 - y/x を満足する関数 y の x = 2 における初期値をEuler法で求めるためのプログラムをPythonで作成してください。ただし Sympy や Scipy.integrate.odeint を使わないこと。インターネットで検索して得たプログラムをそのまま使ったり改変して使っても構いませんが、そのときは取得元のURLを明記してください。

• 同じ微分方程式をRunge-Kutta法で求めるためのプログラムをPythonで作成してください。ただし Sympy や Scipy.integrate.odeint を使わないこと。インターネットで検索して得たプログラムをそのまま使ったり改変して使っても構いませんが、そのときは取得元のURLを明記してください。

補足

Sympy で微分方程式の特殊解を求める時に ics オプションが使えない問題は、演習室にインストールしてある Sympy のバージョンが最新の 1.3 ではなく 1.0 であったことが原因と思われます。権限（permission）がないと演習室のパソコンにインストールできないので、個人のPCをお持ちの方はそちらで試してください。演習室のパソコンへのインストールはこちらからお願いしておきます。

Sympy のバージョンが古くて特殊解が計算できなくても、課題には影響しませんので、バージョンアップができなくても心配しないでください。