この記事は 数学とコンピュータⅡ Advent Calendar 15日目の記事です
数値解析は数学か、、、、、と言われると苦しいところがありますが、、ガチ数学でなくてもOKというのに甘えてエントリします。
ここでは、数値解析の応用分野である構造解析や熱流体解析などのエンジニアリングシミュレーションの基本となる、常微分方程式の初期値問題に関する簡単な数値解析を紹介します。少しでも興味を持ってもらえるとうれしいかぎりです![]()
一般に独立変数$x$に関する関数$y$の$m$階常微分方程式はつぎのとおりです。
$$
\dfrac{dy}{dx}=f(x,y,y',y'',\cdot \cdot \cdot,y^{m-1})
$$
ここで区間$[a,b]$における$x=a$での$m$個の初期値を与え
$$
y(a)=y_0,; y'(a)=y'_0,; \cdot \cdot \cdot,y^{(m-1)}(a)= y^{m-1}
$$
で関数$y$を求める問題を初期値問題と言います。
ここでもっとも簡単な1階常微分方程式の初期値問題を考えます。
$$
\dfrac{dy}{dx} =f(x,y)
$$
ここで$x$の解析領域$[a,b]$を間隔$h$で$n=(b-a)/h$分割して、$x,x_1,x_2,\cdot \cdot \cdot,x_n$からなる区分$i(x_i \leqq x \leqq x_{i+1})$で積分すると次の式になります。
$$
\int_{x_{i}}^{x_{i+1}} \dfrac {dx}{dx}dx =\int_{x_{i}}^{x_{i+1}} f(x,y) dx
$$
これを代数方程式で表すと
$$
y_{i+1} = y_{i} + \int_{x_{i}}^{x_{i+1}} f(x,y) dx
$$
となり、初期値$(x_0,y_0)$を与えて順次解くことで近似解が数列${y_i}$として求められます。
この差分式は$h,x_{i},y_{i}$の値を用いた増分関数$k(x_i,y_i,h)$と刻み幅$h$との積として表されます。
$$
y_{i+1} = y_{i} + hk(x_i,y_i,h)
$$
このように、厳密解ではなく代数方程式による近似解を求めることを数値解析と呼びます。数値解析は、数学や物理学の分野で代数的な方法で解を得ることが不可能な解析学上の問題を数値を用いて近似的に解くときに用いられ、主に計算機をつかって近似解を求めます。
今回は例題として、以下の常微分方程式
\begin{equation}
\dfrac{dy}{dx} = xy
\end{equation}
に初期値$y(0)=1$を与えて、Pythonでいくつかの手法で数値解析してみます!
# 導関数
def divf(x,y):
return x * y
まずは厳密解を求める
今回の例題の常微分方程式は、数値解析するまでもなく手計算で厳密解を求めることができますので、まずは手計算してみます。
常微分方程式を次のように式変形します。
$$
\dfrac {dy}{dx}=xy\rightarrow \dfrac {dy}{y}=xdx
$$
ここで、両辺を積分してみます。
$$
\int \dfrac {dy}{y}=\int xdx
$$
積分の公式をつかうと
$$
ln|y|=\dfrac{1}{2}x^2 +C
$$
となります。(ただしCは任意定数)
よって解は
$$
y = Ce^{1/2x^2}
$$
です。このぐらいの方程式で自然現象がうまくモデル化できれば人類はさほど苦労しないのですが、そうは甘くは無いので、、、厳密解が求まらないものを近似的に解くために数値解析をしていきます。
オイラー法で近似解を求める
関数$y(x)$の$x_i$まわりにおけるテイラー展開は次の式になります。
$$
y(x_{i+1}) = y(x_i) + hy'(x_i) + \dfrac{h^2}{2}y''(x_i)+ \cdot \cdot \cdot
$$
ここで、$y'(x_i)$を$f(x_i,y_i)$で、$y(x_i),y(x_{i+1})$を近似解$y_i,y_{i+1}$であらわすと
$$
y_{i+1} = y_i +hf(x_i,y_i)+\dfrac{h^2}{2}f'(x_i,y_i)+ \cdot \cdot \cdot
$$
となります。この右辺第3項以降を無視して局所打切り誤差を$O(h^2)$とする差分方程式をオイラー法と呼びます。
$$
y_{i+1} = y_i +hf(x_i,y_i)
$$
すごくシンプルです。
Pythonでオイラー法を実装するとつぎのようになります。$x$,$y$で初期値、刻み幅を$h$、$x$の最大値を$b$としています。
# Euler法
def euler(x, y, h, b):
x_ap = [x]
y_ap = [y]
while x <= b:
y += h * divf(x,y)
x += h
y_ap.append(y)
x_ap.append(x)
return x_ap, y_ap
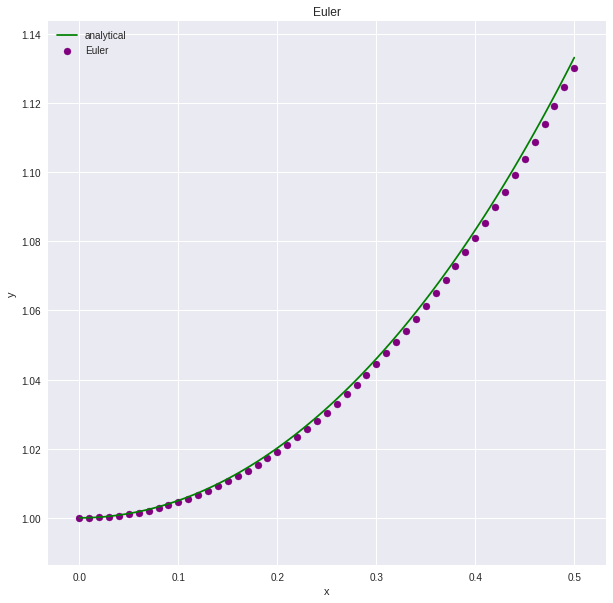
グラフを書いてみます。Eulerでプロットした紫がオイラー法で解いた近似解でanalyticalで表した緑の曲線が厳密解です。ずれてますね、だいぶ![]()
import matplotlib.pyplot as plt
import numpy as np
# グラフ領域の定義
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(1,1,1)
h = 0.01
b = 0.5
# オイラー法のグラフ
x_a , y_a = euler(0.0, 1.0, h, b)
ax.scatter(x_a, y_a, c='purple', label='Euler')
# 厳密解のプロット
x_analytical = np.linspace(0, b, 100)
y_analytical = np.exp(x_analytical * x_analytical * 0.5)
ax.plot(x_analytical,y_analytical,label='analytical', c="green")
# グラフタイトルなどの表示
ax.set_title('Euler')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(loc='best')
ax.grid(True)
数値解析での解析精度は刻み幅$h$に大きく依存します。一般に$h$が小さいほど精度は向上しますが計算回数は$h$に逆比例して増します。また$h$が小さすぎると丸め誤差により誤差が増加したりもします。
Euler法は単純な計算で近似解を求めることができるので数値計算の理解というところでは分かりやすいのですが、誤差が非常に大きいため実用的ではありません。なので、さらに精度の良い手法をかんがえます。
ホイン法で近似解を求める
Eulerは始点における曲線の勾配と刻み幅$h$との積により次の点を予測してます。もし$x_{i+1}$での勾配が予測できればより精度の高い積分ができます。
つまり
$$
y_{i+1}=y_i +\dfrac{h}{2} f(x_i,y_i) + \dfrac{h}{2}f(x_{i+1},y_{i+1})
$$
とし、未知の$f(x_{i+1},y_{i+1})$にオイラーの公式で与えられる値を用いる方法をホイン法といいます。
Pythonでホイン法を実装するとつぎのようになります。$x$,$y$で初期値、刻み幅を$h$、$x$の最大値を$b$としています。
# ホイン法
def imp_euler(x, y, h, b):
x_ap = [x]
y_ap = [y]
while x <= b:
y_1 = y + h * divf(x,y)
y += (divf(x,y) + ((x + h) * y_1)) * h / 2.
x += h
y_ap.append(y)
x_ap.append(x)
return x_ap, y_ap
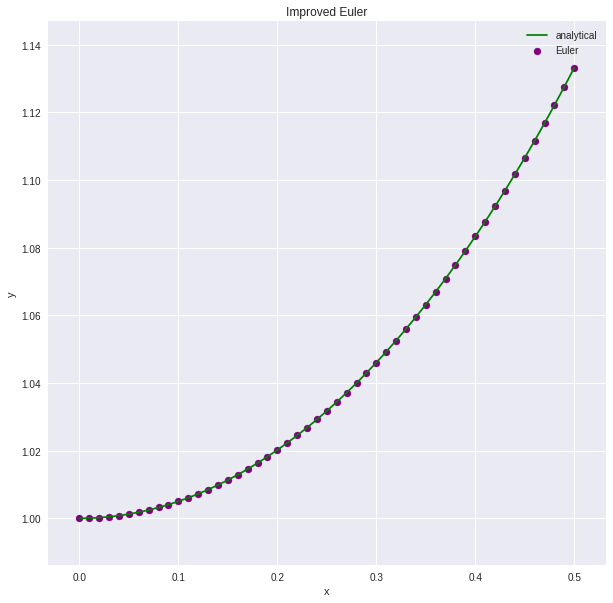
オイラー法に比べるとずいぶん誤差が小さいのがわかります。もうひと頑張り!
ルンゲクッタ法で近似解を求める
関数$y(x)$を$x=x_i$でテイラー展開すると次の式になります。
$$
y(x) = y(x_i)+(x-x_i)y'(x_i) + \dfrac{(x-x_i)^2}{2!}y''(x_i)+\cdot \cdot \cdot
$$
ここで、$x=x_{i+1}=x_i+h$とすると
$$
y(x_{i+1})=y(x_i) + hy'(x_i) + \dfrac{h^2}{2!}y''(x_i)+ \cdot \cdot
$$
となります。ここで
\begin{eqnarray}
k_1 &=& hf(x_i,y_i) \\
k_2 &=& hf(x_i+a_{1}h,y_i + b_1h) \\
k_3 &=& hf(x_i+a_{2}h,y_i + b_{21}k_1 + b_{22}k_2) \\
k_4 &=& hf(x_0+a_{3}h,y_i + b_{31}k_1 + b_{32}k_2 +b_{33}k_3)
\end{eqnarray}
とし、
$$
y_{i+1} = y_i +c_ik_1 + c_2k_2 + c_3k_3 + c_4k_4
$$
として解く方法を、ルンゲクッタ法と呼びます。
ルンゲクッタ法にはいろいろな種類があり、それによって$c$の値が異なるのですが、一番有名な4段4次精度陽的ルンゲクッタ法は、初期条件を$(x_0,y_0)$とし、刻み幅を$h$とすると
\begin{eqnarray}
x_{i+1} &=& x_i +h \\
y_{i+1} &=& y_i +\dfrac{1}{6}(k1 + 2k_2 + 2k_3 +k_4)
\end{eqnarray}
であわらされます。
ここで4段4次精度陽的ルンゲクッタ法は、係数$k$をそれぞれ
\begin{eqnarray}
k_1 &=& f(x_i,y_i)h \\
k_2 &=& f(x_i + \dfrac{h}{2},y_i + \dfrac{k_1}{2})h \\
k_3 &=& f(x_i + \dfrac{h}{2},y_i + \dfrac{k_2}{2})h \\
k_4 &=& f(x_i + h,y_i + k_3)h
\end{eqnarray}
として解を求めます。
4段4次精度陽的ルンゲクッタ法をPythonで実装するとこんな感じです。
# RK4法
def rk4(x, y, h, b):
x_ap = [x]
y_ap = [y]
while x <= x_max:
k1 = h * divf(x,y)
k2 = h * ((x + (h / 2.0)) * (y + (k1 / 2.0)))
k3 = h * ((x + (h / 2.0)) * (y + (k2 / 2.0)))
k4 = h * ((x + h) * (y + k3))
y += (k1 + 2.0 * k2 + 2.0 * k3 + k4) / 6.0
x += h
y_ap.append(y)
x_ap.append(x)
return x_ap, y_ap
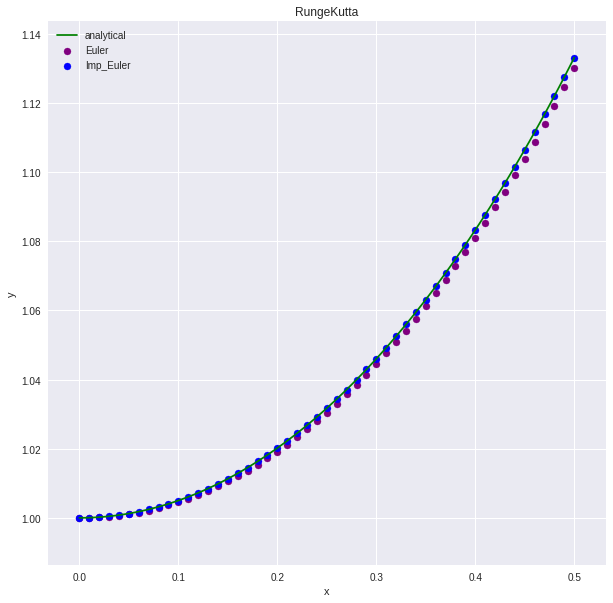
グラフで見てみるとなかなか良い精度です。
ルンゲクッタ法は刻み幅が荒くても精度よく計算できるという特徴があります。ここで$h$を10倍の荒さの0.1にしてオイラー法とルンゲクッタ法で厳密解との誤差を見てみると、一目瞭然です。
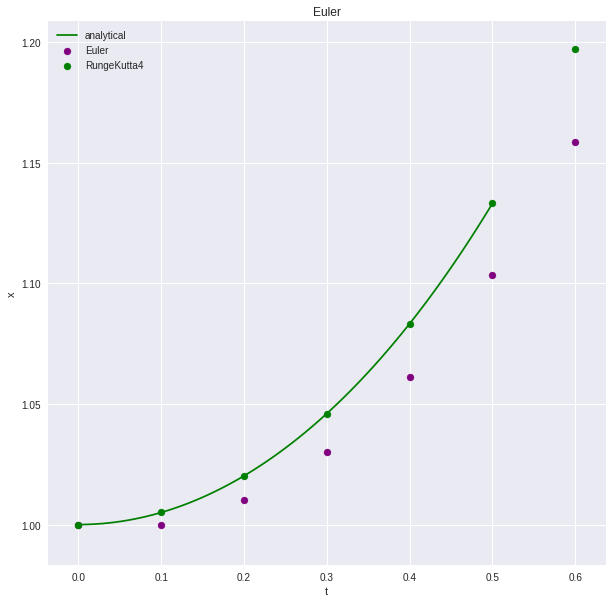
計算機を使った数値解析ではかならず誤差を含みます。離散化誤差や丸め誤差などで、差分式による近似解がもとの常微分方程式とはまったく異なる解になってしまうことがあるので注意が必要です。
あと、数値解析はなるべく計算量を抑え、いかに精度の良い解を収束させるかに身骨を砕く世界です。今回の例ではまったくうれしさが分かりませんが、大規模な計算になると並列分散計算をするので、効率の良いアルゴリズム大事です。
数値解析の注意点
解析では誤差以外にもいくつか気を付けることがあります。
数値解析の収束性
数値解析では、刻み幅$h$を限りなく小さくしたときに近似解$x_n$が厳密解$x_(t_n)$に近づくことを収束すると言います。これは
$$
\lim_{h \to 0} x(t_j)
$$
をみたすとき
$$
\lim_{h \to 0} \left( \max_{k<n<N} |x_n-x(t_j)| \right)=0
$$
がなりたつとき、解が収束するということになります。ただしこれは無限このステップ数を増やせば真の解が得られるといっていることになりますので、一般的には
$$
|x_n-x(t_j)| \leq C_0 h^p (j = 0,1,\cdot \cdot \cdot,k-1)
$$
のもとで
$$
\max_{k<n<N} |x_n-x(t_j)| \leq Ch^p
$$
となる指数$p$を与えます。ここで$h$は十分小さいものとし、$C_0,C$は$h$に依存しない定数です。このとき、近似解は$\mathcal{O}(h^p)$で収束する、といいます。
数値解析の安定性
数値解析では、近似解が上下に激しく振動することがあります。これを数値的不安定現象と呼びます。微分方程式を今回のような差分法で解くときの数値的安定性を調べるのに使われる手法で、フォンノイマンの安定性解析というものがあります。
以前にメモしたブログですが、、、
クランクニコルソン法とフォンノイマンの安定性についてはこちらにまとめています。
http://dr-asa.hatenablog.com/entry/2017/08/31/154806
まとめ
だらだらと長くなりましたが、数値解析がわかるようになると、常微分方程式や偏微分方程式の近似解を計算機を使って求めることができます。これを応用すると物理現象を偏微分方程式で表現した支配方程式を解くことでシミュレーションができます。楽しい![]()
機械学習より少ない数学の知識(解析学と初歩的な線形代数のみ)ではじめられますので、理系の大学教養部で学ぶ数学のやり直しにもおすすめです。
参考文献
- 数値計算入門 サイエンス社 河村哲也著/2006年
- 微分方程式による計算科学入門共立出版社株式会社 三井 斌友/小藤 俊幸/斉藤 善弘 著/2004年