Pythonで数値計算プログラムを書き直そうシリーズ
「ここ、こうすればいいのに」とかあれば教えてください(土下座)
はじめに
非線形方程式の数値解法と言えば、Newton法が二分法と並んでよく取り上げられます。関数の傾きを利用して、二分法よりも速く非線形方程式の解を見つける方法だとされます。Qiitaの既存記事のリンクも貼っておきます。
Python - 非線形方程式解法 二分法 & ニュートン・ラフソン法
C言語で学ぶニュートン法
根の探索アルゴリズム
非線形方程式をpythonで解く
完成したプログラム
# Newton法による非線型方程式の解法プログラム
import numpy as np #NumPyライブラリ
import matplotlib.pyplot as plt #データ可視化ライブラリ
# 解きたい方程式
def func_f(x):
return x**2.0 -2.0
# Newton法(方程式の関数項、探索の開始点、微小量、誤差範囲、最大反復回数)
def newton(func_f, x0, eps=1e-10, error=1e-10, max_loop=100):
num_calc = 0 #計算回数
print("{:3d}: x = {:.15f}".format(num_calc, x0))
#ずっと繰り返す
while(True):
#中心差分による微分値
func_df = (func_f(x0 +eps) -func_f(x0 -eps))/(2*eps)
if(abs(func_df) <= eps): #傾きが0に近ければ止める
print("error: abs(func_df) is too small (<=", eps, ").")
quit()
#次の解を計算
x1 = x0 -func_f(x0)/func_df
num_calc += 1 #計算回数を数える
print("{:3d}: x = {:.15f}".format(num_calc, x0))
#「誤差範囲が一定値以下」または「計算回数が一定値以上」ならば終了
if(abs(x1-x0)<=error or max_loop<=num_calc):
break
#解を更新
x0 = x1
#最終的に得られた解
print("x = {:.15f}".format(x0))
return x0
# 可視化(方程式の関数項、グラフ左端、グラフ右端、方程式の解)
def visualization(func_f, x_min, x_max, x_solved):
plt.xlabel("$x$") #x軸の名前
plt.ylabel("$f(x)$") #y軸の名前
plt.grid() #点線の目盛りを表示
plt.axhline(0, color='#000000') #f(x)=0の線
#関数
exact_x = np.arange(x_min,x_max, (x_max-x_min)/500.0)
exact_y = func_f(exact_x)
plt.plot(exact_x,exact_y, label="$f(x)$", color='#ff0000') #関数を折線グラフで表示
plt.scatter(x_solved,0.0) #数値解を点グラフで表示
plt.text(x_solved,0.0, "$x$ = {:.9f}".format(x_solved), va='bottom', color='#0000ff')
plt.show() #グラフを表示
# メイン実行部
if (__name__ == '__main__'):
#Newton法で非線型方程式の解を計算
solution = newton(func_f, -2.0)
#結果を可視化
visualization(func_f, solution-1.0, solution+1.0, solution)
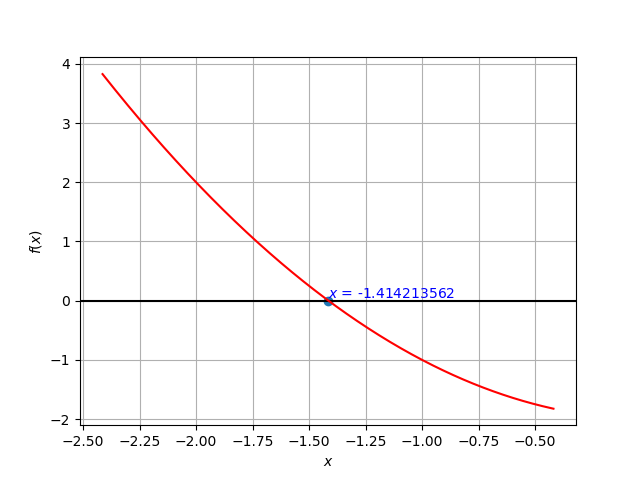
中心となるプログラムはnewton関数です。引数として、方程式の関数項$f(x)$、探索の開始点の2つを渡すと、方程式$f(x)=0$の解を「一つだけ」求めます。オプションとして、誤差範囲、差分計算に使う微小量、最大反復回数を変えることもできます。上のプログラムでは$x^2-2=0$の解を、$x=-2$の点から探します。実行すると、計算回数4回目で$x = -1.41421356237$と計算されました。
個人的にモジュールとして呼び出し可能にしたかったので、そういう構造になっています。モジュールとして使うテストプログラムは以下に書きました。方程式$x^2 -3=0$と、$arctan(x)=0$の解を求めるプログラムになっています。
import numpy as np #数値計算用モジュール
import newton
def func_f1(x):
return x**2.0 -3.0
solution1 = newton.newton(func_f1, 1.0, error=1e-15)
newton.visualization(func_f1, solution1-1.0, solution1+1.0, solution1)
def func_f2(x):
return np.arctan(x)
solution2 = newton.newton(func_f2, 2.0)
newton.visualization(func_f2, solution2-1.0, solution2+1.0, solution2)
実行すると分かりますが、$arctan(x)=0$の解を計算しようとすると、解が発散してプログラムが止まります(プログラム上では発散する前に止めています)。
注意すべきと思う点
二分法の項目で書いた内容は省略します。
関数の微分は差分で求める
Newton法を勉強してまず面倒だと思うのが、「関数の微分を求めておく必要がある」ことだと思います。線形多項式や三角関数程度ならまだいいですが、$arctan(x)$の微分とかになると、頭スパース人間の自分はもう嫌になってしまいます。なんにせよ、問題を解く度に毎回微分を計算するのは実用的ではありません。
やや発展的な解決法になりますが、微分の計算には差分を使うのが良いと思います。とは言え、差分の計算自体はテイラー展開の式から求まりますし、微分方程式の数値解法関係を調べれば情報は見つかります。今回は中心差分を用いました。微小量をいくつにすべきか迷いましたが、ひとまずlimit=1e-10を与えました。ちなみに、中心差分などについては、いずれ差分法の記事で扱う予定です。
関数と初期値によっては解が振動・発散する
上のプログラムでは、$arctan(x)=0$を上手く計算できませんでした。数値計算本にも説明がないことがありますが、実はNewton法は、方程式の根の付近に変曲点があったりすると、解が振動したり、発散してしまうことがあります(解の初期値にも依存する)。$arctan(x)=0$の場合、解である$x=0$から離れるにつれて関数の傾きが0に近づくので、探索途中の解が振動しながら遠くに飛んでいき、やがて発散してしまいます。同様の理由で、3次以上の線形多項式や三角関数などの場合でも、探索点がたまたま極値に近かったりすると、解の初期値から随分離れた所の解を見つけてきたりします。今回は傾きがほぼ0だったらプログラムを止めるようにしました。
そんな訳で、二分法とNewton法を比べる内容を読むと、「アルゴリズムの工夫でNewton法の方が解を速く求められる」みたいな書き方をよくされていますが、実際にはNewton法は関数によって解が振動したり発散したりするので、どちらも一長一短あると捉えるのが無難なのではと思っています(あくまでも自分の理解ですが)。
自作プログラムは使えるのか
例のごとく、SciPyでもNewton法を使えてしまいます。おまけに微分も求めなくていいです。今回のプログラムと同じように、微分を差分で求めていると思われます。また参考として、非線形方程式の解法によく使われるらしい、二分法を改良したBrent法(scipy.optimize.brent)による解法も載せておきます。
import scipy.optimize
def func_f1(x):
return x**2.0 -2.0
# Newton法
result1 = scipy.optimize.newton(func_f1, 1.0)
print(result1)
# Brent法
result2 = scipy.optimize.brentq(func_f1, 1.0, 2.0)
print(result2)
また、複数の解を一度に求めたいなら、二分法の記事でも触れたSymPyが最強だと思います。これだけで、[-1.41421356237310, 1.41421356237310]と全ての解が表示されます。
→と、思ったら解けないこともあるようです。解けない時は「No algorithms are implemented to solve equation」と出ます。
import sympy
x = sympy.Symbol("x")
result = sympy.solve(x**2.0 -2.0, x)
print(result)