ある関数 $f(x)$ の根, すなわち $f(x^*) = 0$ を満たす $x^*$ の探索について, もし $f$ が微分可能であれば微積分の知見を用いて根を見つけることは容易である. 本稿では関数 $f$ が微分不可能, もしくは具体的な関数の形が分かっていない等で導関数が計算不可能な場合に数値計算の観点から関数の根の近似解を求める方法を紹介する.
二分法(Binary method)
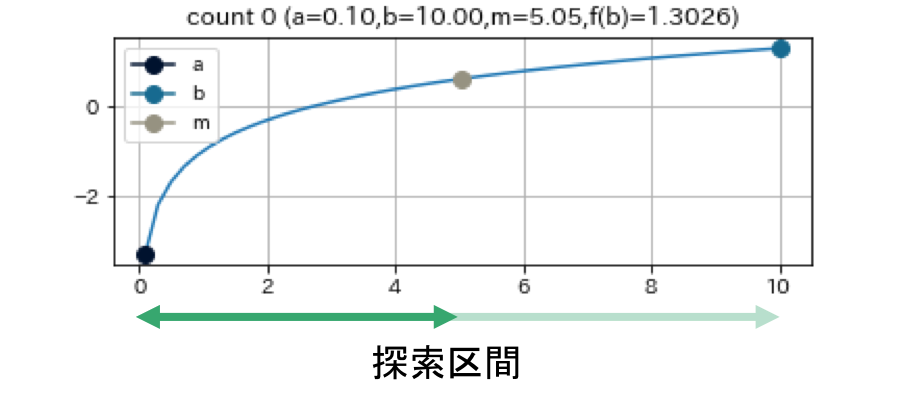
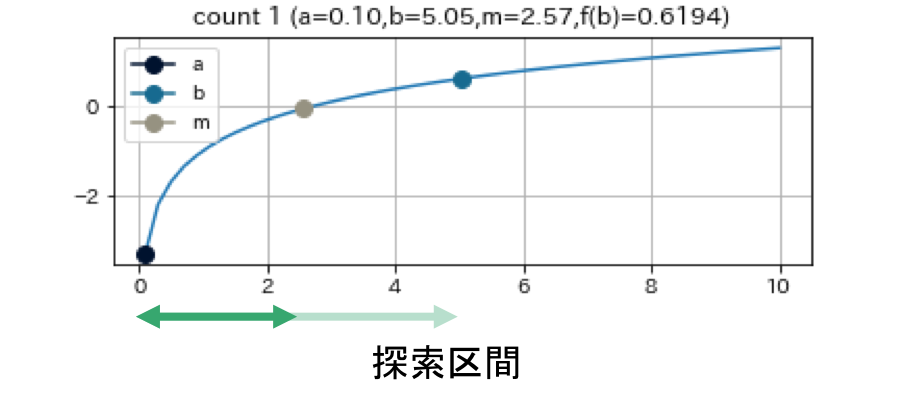
二分法は探索区間$[a, b]$を半減させながら, 根へと収束させる方法である. ここでいう探索区間とは, 根が存在するであろう範囲のこと. たとえば関数 $f$ が連続関数でかつ $f(a)f(b) < 0$ すなわち $f(a)$ と $f(b)$ の符号が異なるとき, 中間値の定理より区間 $[a, b]$ の中に根が存在する. またこのとき, この区間を初期探索区間として採用すれば二分法を用いることで, 指定した精度に有限回の試行回数で収束できることが保証されている1.
二分法のアルゴリズは次のようなシンプルなもの.
- 探索区間をまず2等分し
- そのうち根が必ず存在するほうを次の探索区間として採用する.
根が必ず存在するかどうかは前述した探索区間の単点と中間点における関数の符号を見れば良い。
input: function f
input: point a, b such that f(a)f(b) < 0 and |f(b)| < |f(a)|
constant: e 許容誤差
while |f(b)| > e
m = (a + b) / 2
if f(a)f(m) > 0:
a = m
else:
b = m
if |f(a)| < |f(b)|: # bが最適な値にする
a, b = b, a
return b
変数の持つ意味合いは次に書くとおり.
a: 探索区間の端点のうちbではないほう
b: 各ループ終了時における最適値
m: 二分法による新しい探索点
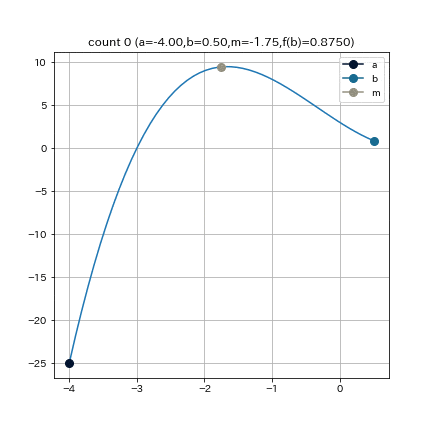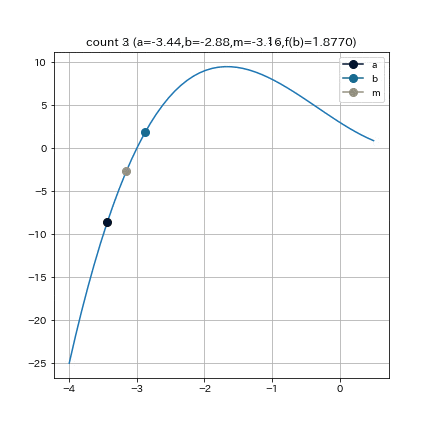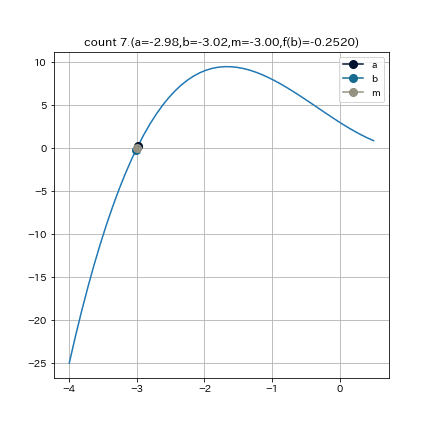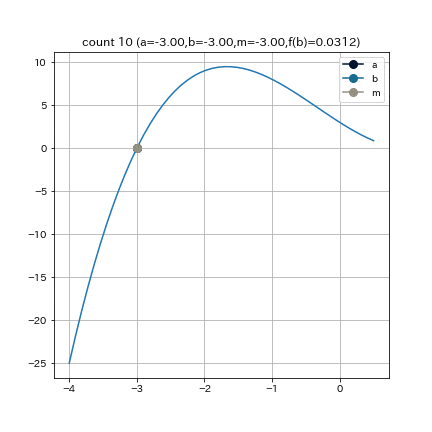
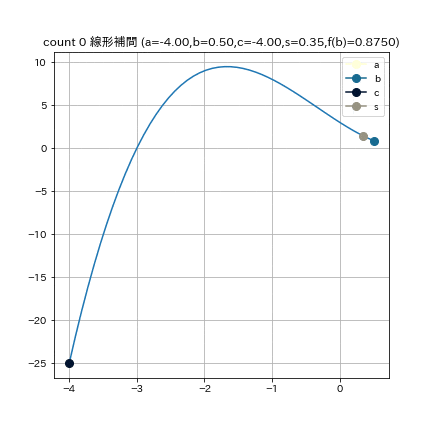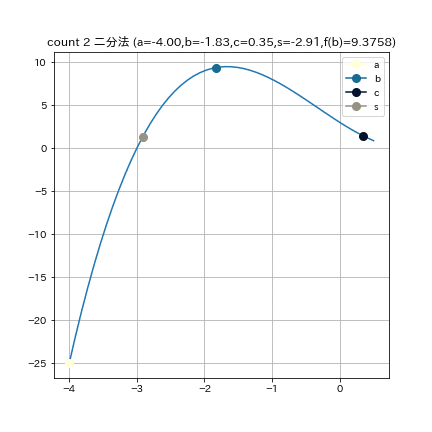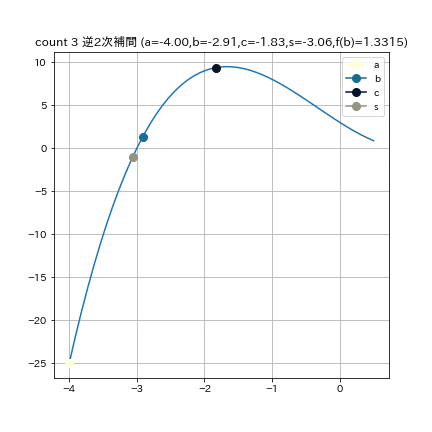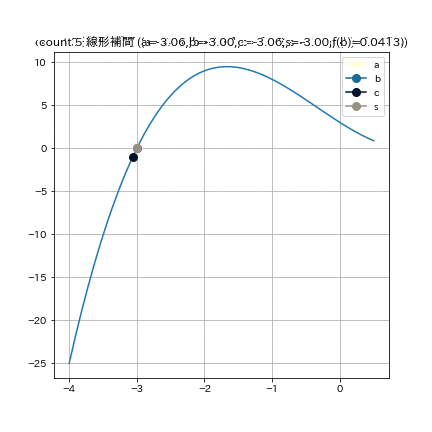
この図は $f(x) = (x+3)(x-1)^2$という関数で $a = -4, b = 0.5, e = 0.01$ として二分法を実行した結果である.
利点: 収束の堅固さ(ロバスト性)
欠点: 収束の遅さ
収束次数は1.
割線法(Scant method)
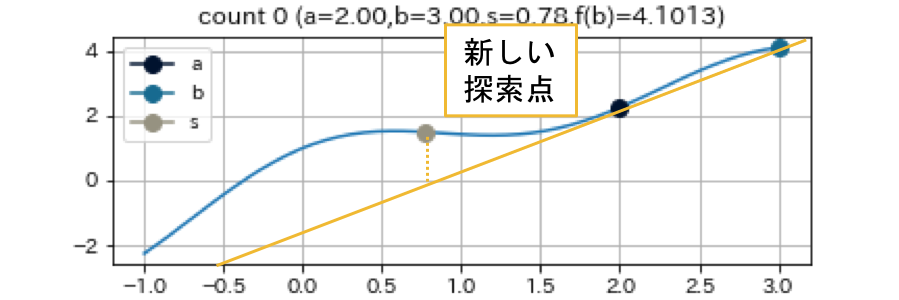
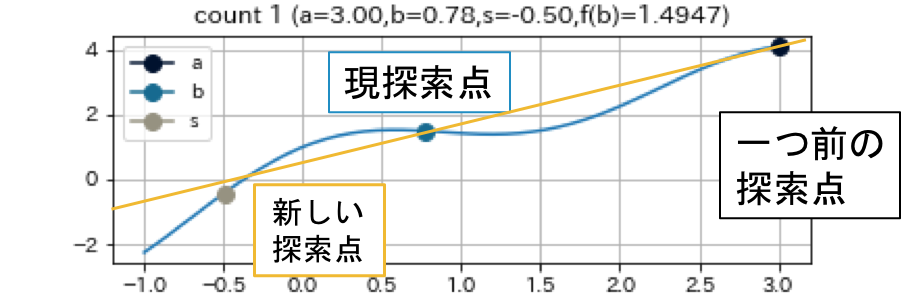
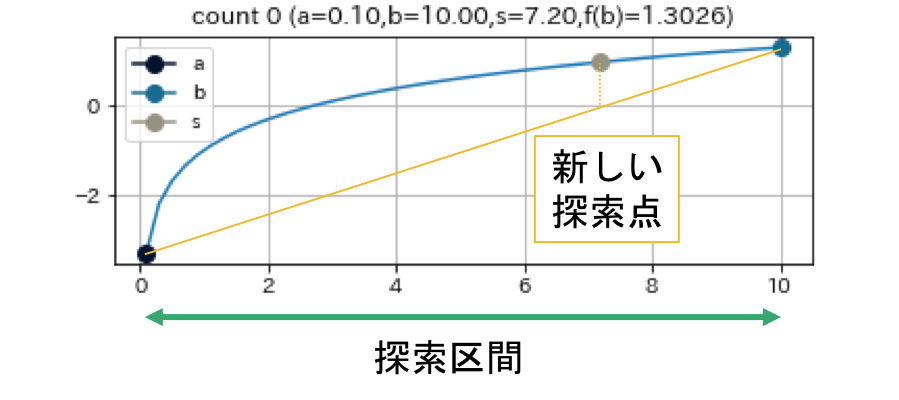
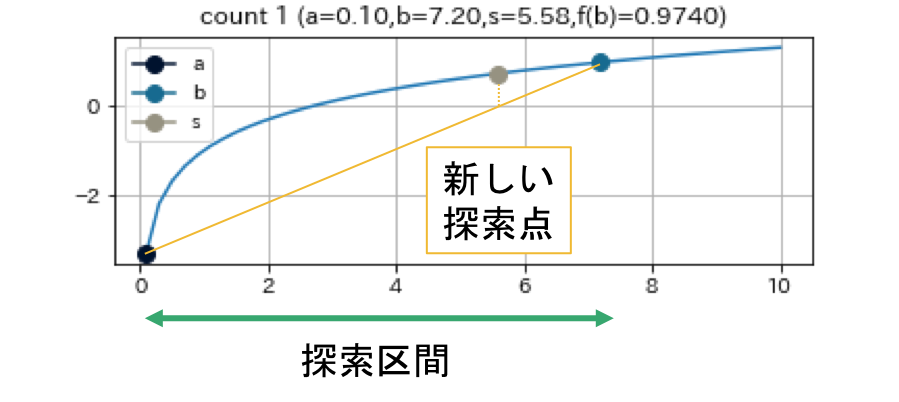
割線法は現在の探索点 $b$ と一つ前の探索点 $a$ を直線で結び, その直線と $y=0$ との交点を次の探索点とする手法である2.
Newton法で用いる導関数を2点間での数値微分で代用することに相当する. 下で示す例からも見てとれるように, 根の周辺で関数が直線的であると, 非常に早く収束する. 特筆すべき点として, 二分法とは違い, $f(a)f(b)<0$ を満たす $a, b$ を求める必要がない3.
input: function f
input: point a, b
constant: e 許容誤差
while |f(b)| > e
s = (a*f(b)-b*f(a))/(f(b)-f(a))
a, b = b, s
return b
a: 一つ前の探索点
b: 現在の探索点
m: 割線法による新しい探索点
なお, $b$ と $a$ による直線補間と $y=0$ との交点は単純に, $s = b - f(b)\cfrac{b-a}{f(b)-f(a)}$ とも書けるが, 実際には $s = \cfrac{af(b) - bf(a)}{f(b)-f(a)}$ で計算する方が良い. それは何故かというと, 収束が進むにつれ, b と a は同じような値を取ることになるが, このとき b-a を計算するといわゆる桁落ちが生じてしまう. そのとき生じる数値誤差により収束速度が遅くなってしまう恐れがある4. (しかしながら, fが連続関数である場合, bとaが近ければ,f(b)とf(a)も近い値になるので, 結局同じことではないかと筆者=私は感じている)
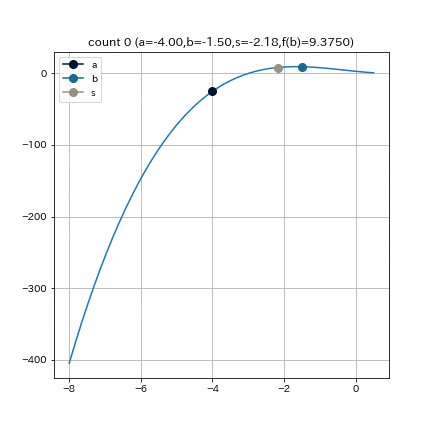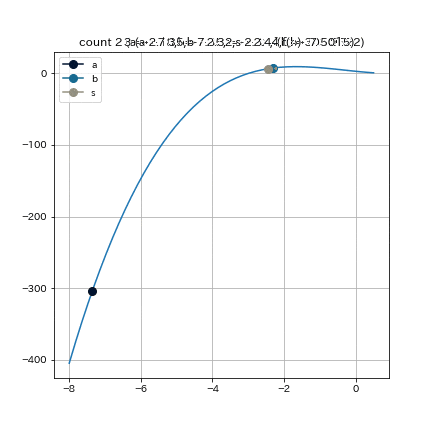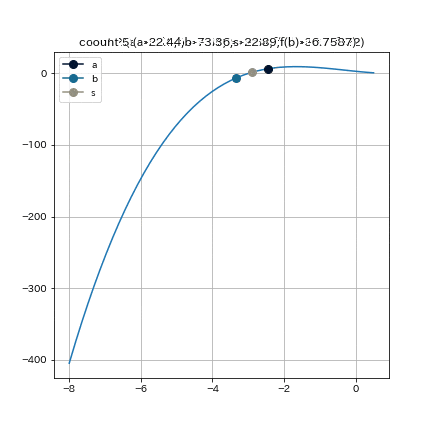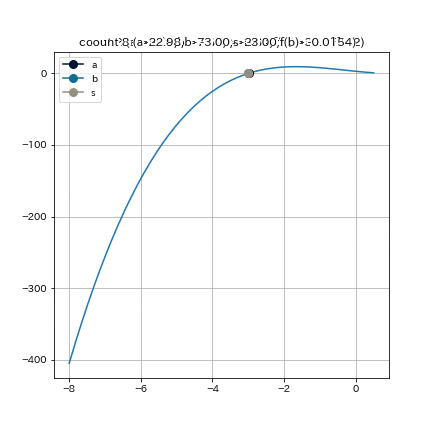
これは, $f(x) = (x+3)(x-1)^2$ という関数で, $a = -4, b = -1.5, e = 0.01$ として, 割線法を実行した結果である.
利点: 根の周辺が線形であれば, 最後の数回の収束が早い
欠点: 収束しない場合がある
Coming Soon 収束しない例
挟み撃ち法(False position method)
二分法のように根が存在するであろう探索区間を保ちながら, 次の探索点としては直線補間を用いるのが挟み撃ち法である. 割線法と異なるのは探索区間の2端点から直線補間を行う点である4.
input: function f
input: point a, b such that f(a)f(b) < 0 and |f(b)| < |f(a)|
constant: e 許容誤差
while |f(b)| > e
s = (a*f(b)-b*f(a))/(f(b)-f(a))
if f(a)f(s) > 0:
a = s
else:
b = s
if |f(a)| < |f(b)|: # bが最適な値にする
a, b = b, a
return b
ある探索区間 $[a, b]$ について, $f(a) \neq 0$と$f(b) \neq 0$ の符号が異なるならば, $a$ と $b$ を補間した直線と $y=0$ との交点は開区間 $(a, b)$ 上に存在する. すなわち一回のループごとに必ず探索区間は小さくなる.
利点: 収束の堅固さ
欠点: 収束が遅い場合がある
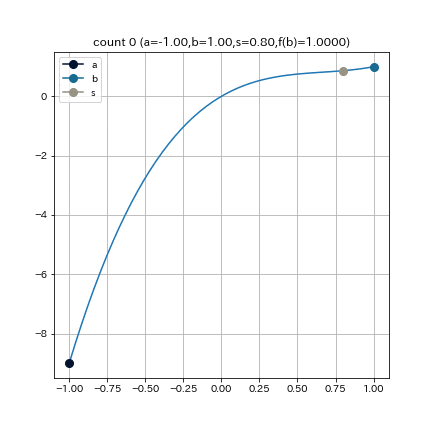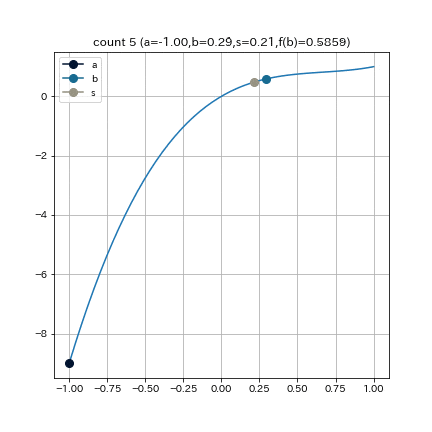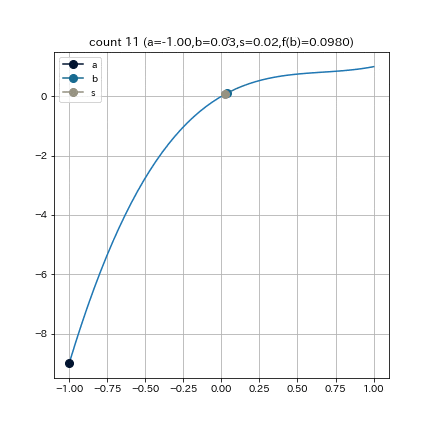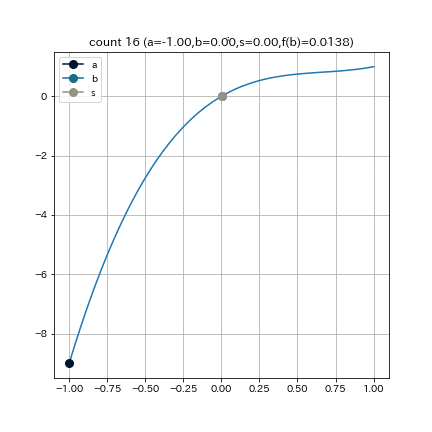
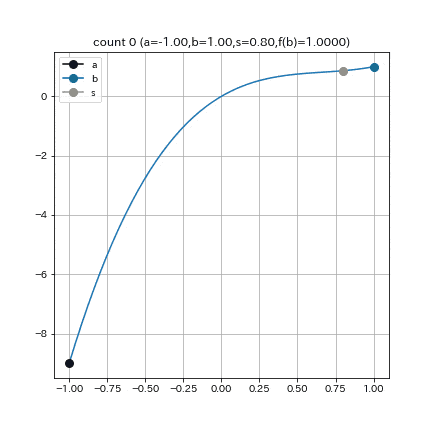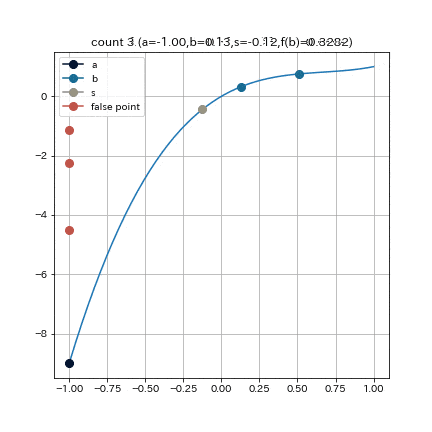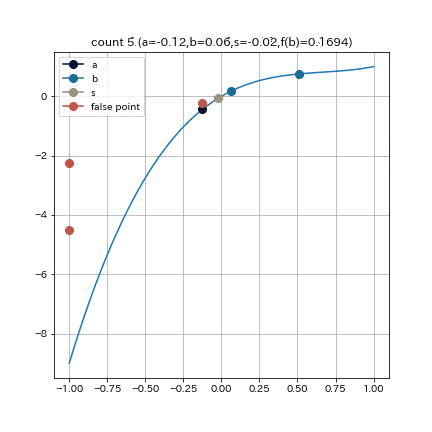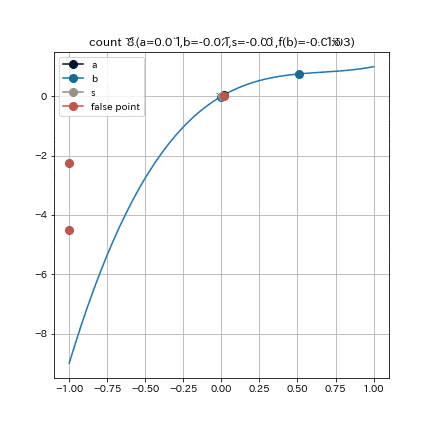
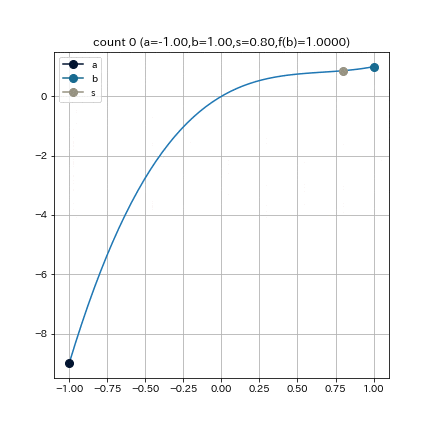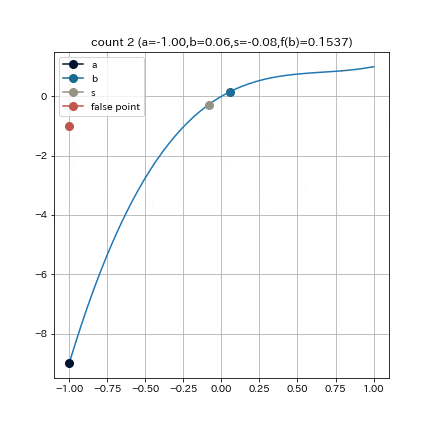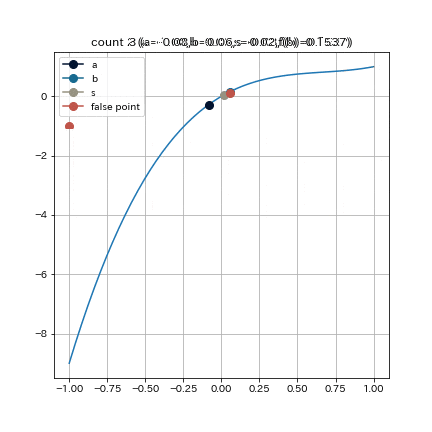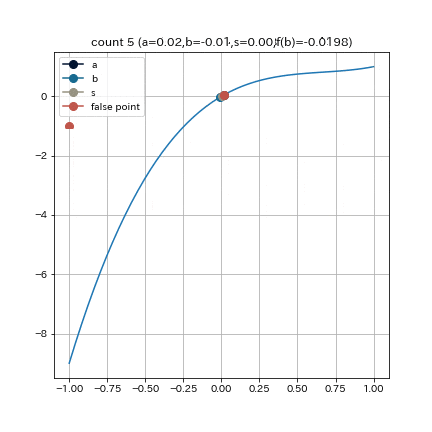
これは, $f(x) = 2x^3 - 4x^2 + 3x$, $a = -1, b = 1, e = 0.01$ として探索を始めた結果である. これを見ると, 前半から後半にかけて更新の歩みが遅くなっていることがわかる. 原因としては, 左端点($x=-1$)が探索中全く動かないことから探索区間が縮まらず, 各ループにおける線形補間の精度が悪いことが考えられる.
そこで次のような, 改善策が考えられる.
イリノイ法(Illinois method)
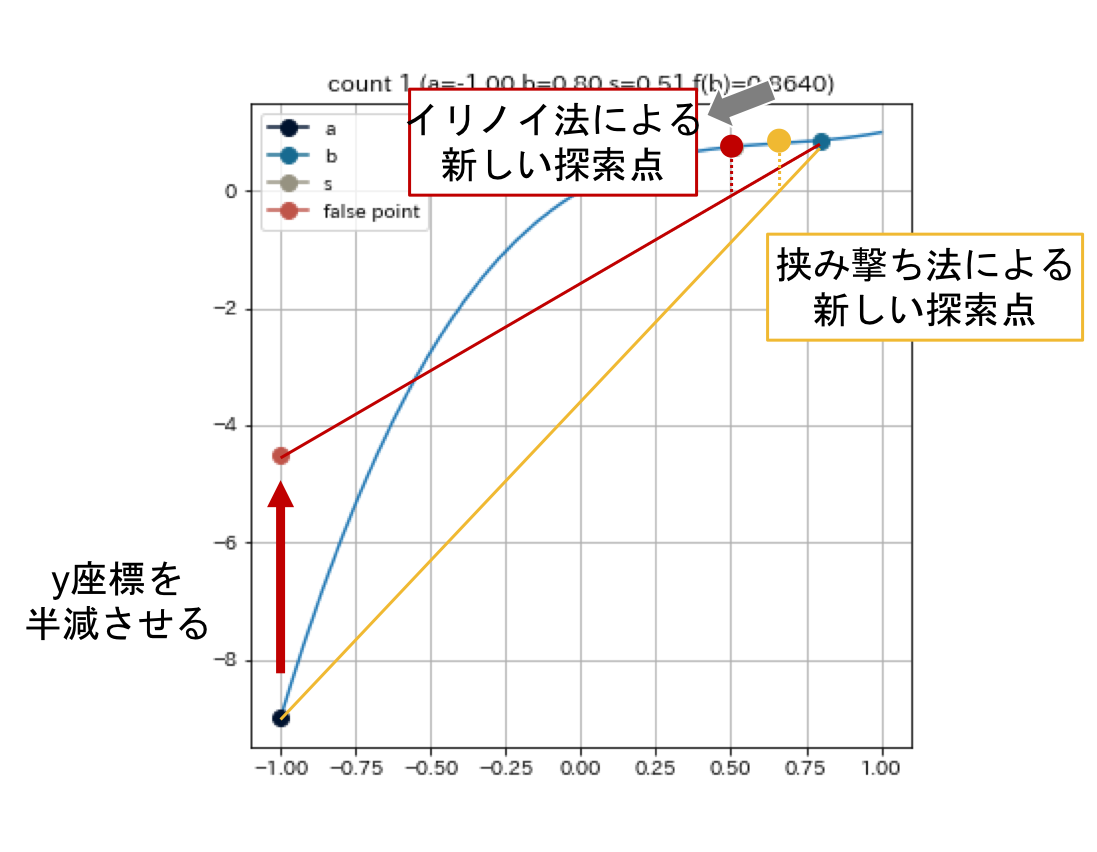
探索区間の両端により線形補間を行うのではなく, 片方を仮想的な点に置き換えて線形補間を行うというアイデアである. 探索区間の端点を$a, b$とする. このとき, 次の探索点を $s = \cfrac{af(b)-bf(a)}{f(b)-f(a)}$ ではなく, $s = \cfrac{af(b)-b\frac{f(a)}{2}}{f(b)-\frac{f(a)}{2}}$ もしくは, $\cfrac{a\frac{f(b)}{2}-bf(a)}{\frac{f(b)}{2}-f(a)}$を採用する. すなわち, 片方の端点の$y$座標を半減させて線分補間を行う4.
上の図では, $a$ の $y$ 座標を半減させており, 探索点 $s$ (図中, 灰色丸点)が $a$ の方に近づく様子を示した, 探索点 $s$ が $a$ に近づくということは探索区間の$a$が$s$に置き換わりやすくなることを意味する. 探索区間の両端を更新させやすくするために, 前のループで更新されなかった方の端点の $y$ 座標を半減させるということを行う.
input: function f
input: point a, b such that f(a)f(b) < 0 and |f(b)| < |f(a)|
constant: e 許容誤差
fa = f(a)
fb = f(b)
while |fb| > e
s = (a*fb-b*fa)/(fb-fa)
fs = f(s)
if fa*fs > 0:
a = s; fa = fs
fb = fb / 2 # 更新されなかった方の端点のy座標を半減
else:
b = s; fb = fs
fa = fa / 2 # 更新されなかった方の端点のy座標を半減
if |fa| < |fb|: # bが最適な値にする
a, b = b, a
fa, fb = fb, fa
return b
これは, $f(x) = 2x^3 - 4x^2 + 3x$, $a = -1, b = 1, e = 0.01$として探索を始めた結果である. 割線法が17回のループで探索を終了したのに対し, イリノイ法では9回のループで探索を終えることができている. また, 途中で割線法による更新を適宜挟むなどの工夫をすれば, より高速に探索を行えるだろう.
アンダーソン・ビョーク法(Anderson & Björk's method)
さらにイリノイ法に工夫を加えたのが, このアンダーソン・ビューク法である. イリノイ法では, 更新されなかった端点の$y$座標を常に半減させていたが, この手法では新しい探索点の具合からどれだけ減らすかを決定する4. 具体的な決め方は以下の通り.
探索区間の端点 $a, b$ について, 新しい探索点$s$を得たとする. 端点 $a$ を $s$ に更新するならば, 次の探索点計算において $fb$ を $fb \leftarrow m * fb$ と更新する. このとき, $m$ は $m = 1 - \cfrac{f(s)}{f(a)},,,if,,,\cfrac{f(s)}{f(a)} < 1,,,else,,,\cfrac{1}{2}$ とする.
挟み撃ち法やイリノイ法よりも, より根に近い値が探索点として採用されていることが分かる.
input: function f
input: point a, b such that f(a)f(b) < 0 and |f(b)| < |f(a)|
constant: e 許容誤差
fa = ori_fa = f(a)
fb = ori_fb = f(b)
while |fb| > e
s = (a*fb-b*fa)/(fb-fa)
fs = f(s)
if fa*fs > 0:
m = 1 - fs / ori_fa if fs / ori_fa < 1 else 1 / 2
a = s; fa = original_fa = fs
fb = m*fb # 更新されなかった方の端点のy座標をm倍減少
else:
m = 1 - fs / ori_fb if fs / ori_fb < 1 else 1 / 2
b = s; fb = original_fb = fs
fa = m*fa # 更新されなかった方の端点のy座標をm倍減少
if |fa| < |fb|: # bが最適な値にする
a, b = b, a
fa, fb = fb, fa
ori_fa, ori_fb = ori_fb, ori_fa
return b
これは, $f(x) = 2x^3 - 4x^2 + 3x$, $a = -1, b = 1, e = 0.01$ として探索を始めた結果である. 割線法が17回, イリノイ法では9回のループで探索を終えているのに対し, このアンダーソン・ビョーク法では6回で探索を終えることができた.
この $m$ の決め方について次のように考察した. 各ループにおいて線形補間による端点の更新が小さければ, もう片方の端点の減少率を上げるという式になっているが, これは更新されなかった方の端点の更新を促しているといえる. 両端が大きく更新されていくのが理想的な探索であるが, あるループで小さい更新が起こると, もし関数が連続的であれば次のループでも同じ側でまた小さい更新が起きやすい.
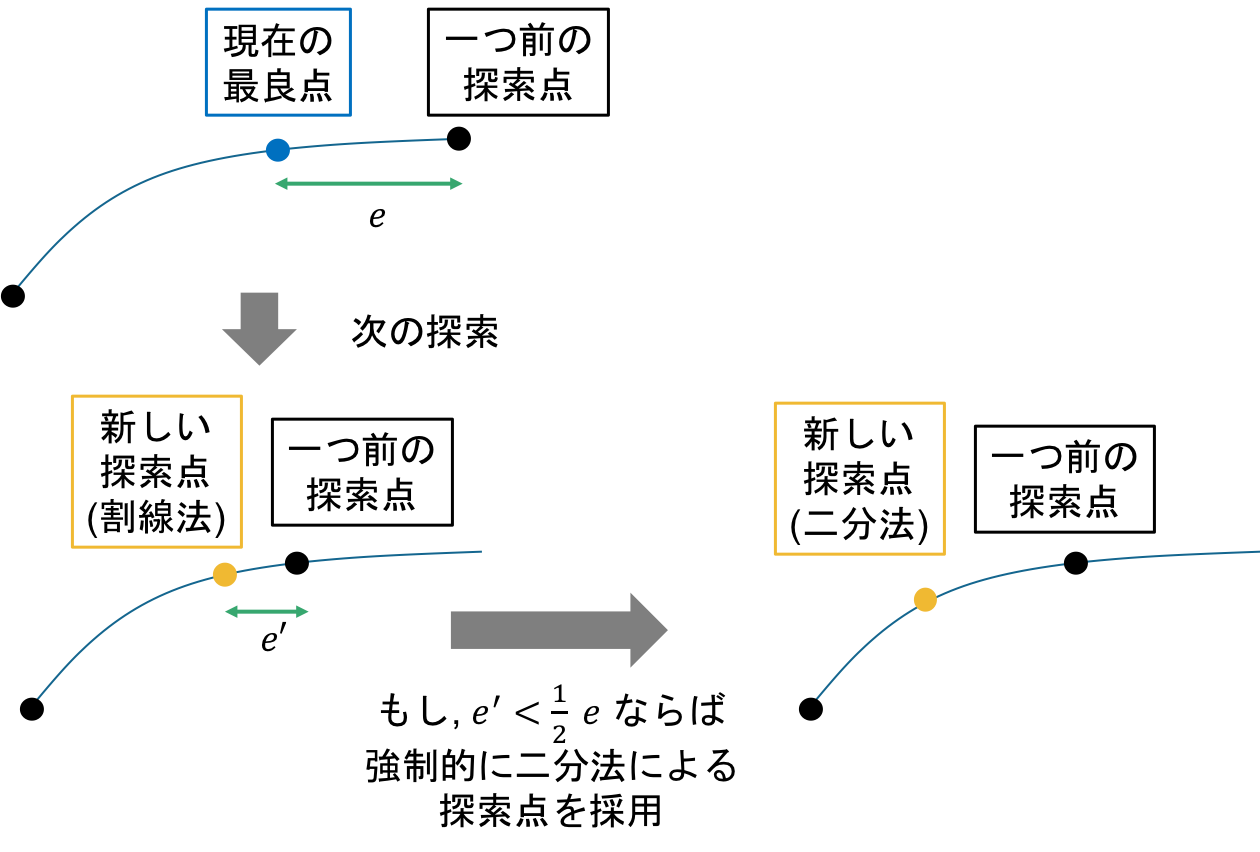
デッカー法(Dekker method)
デッカー法は二分法と割線方を単純に組み合わせた手法である. 現在の探索状況から, 二分法と割線法によりそれぞれ探索点を計算し, 次の探索点として, そのどちらかを採用することで, 二分法と割線法のいいとこ取りと欠点の補い合いを行う[5][Dekker, 1969, Finding a zero by means of successive linear interpolation, in Dejon and Henrici].
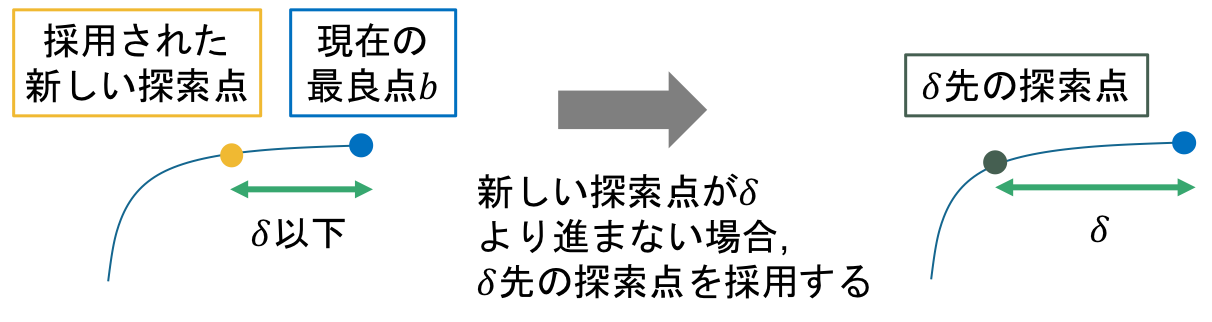
ただし割線法による新しい探索点が採用された場合, 探索点がほとんど進まない場合がある. それを避けるために, 最低ステップ幅 $\delta > 0$ を予め決めておき, 探索中最適 $\delta$ は進むようにする.
input: function f
input: point a, b such that f(a)f(b) < 0 and |f(b)| < |f(a)|
constant: e 許容誤差
c = a
while |f(b)| > e
s = (a*f(b)-b*f(a))/(f(b)-f(a))
m = (a + b) / 2
c = b
if |b - m| < |b - s|: # mがsよりもbに近い
b = m
else: # sがmよりもbに近い
b = s
if f(a)f(b) > 0:
a = c
if |f(a)| < |f(b)|:
a, b = b, a
return b
a: 探索区間の端点のうちbではないほう
b: 各ループ終了時における最適値
m: 二分法による新しい探索点
s: 割線法による新しい探索点
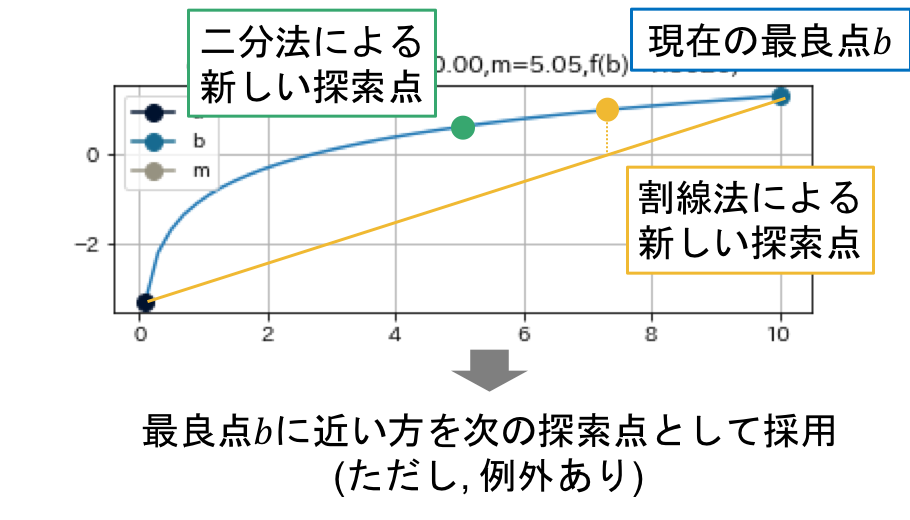
各ループ終了時にはbが最適値になっていることに留意すると, mとsのどちらを選ぶかをbに近い方を選択するのは自然のように思える.
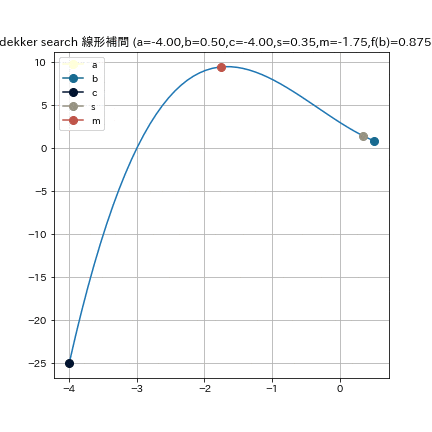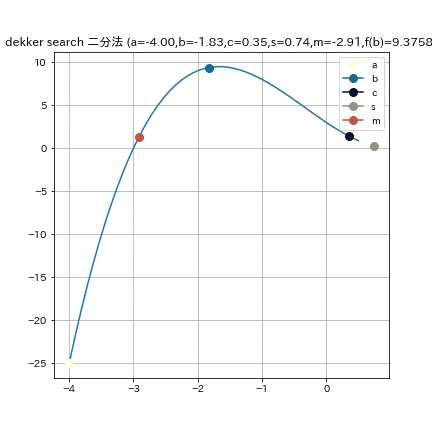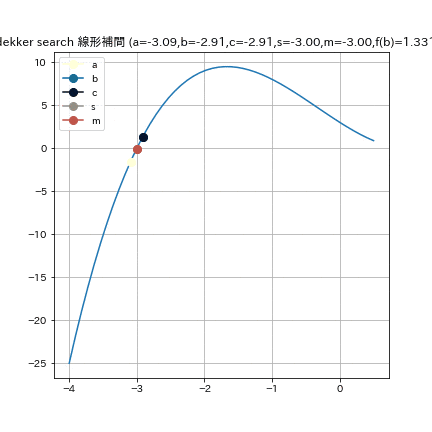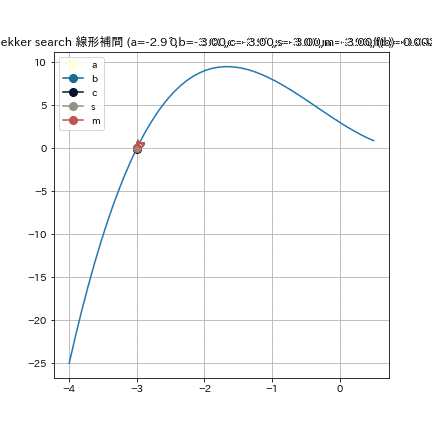
これは, $f(x) = (x+3)(x-1)^2$という関数で, $a = -4, b = 0.5, e = 0.01$として, 二分法を実行した結果である.
また, $f(a)f(b) < 0$ を満たす, $a, b$ が見つかっていない状況でも, 最初はデッカー法の割線法による探索のみを行い, 探索中に $f(a)f(b) < 0$ を満たす, $a, b$ が見つけられれば, 二分法による探索も追加するという変更を加えれば良い.
利点: 必ず収束し(二分法), 根の近くが線形であれば最後の数回の収束が早い(割線法)
欠点: それぞれの手法, 特に割線法での探索点が常に採用されると, 融合したうまみがなくなってしまう
Coming Soon 欠点を表わす例
このような問題を回避するために, ブレントは次のようにデッカーのアルゴリズムを改良した.
ブレント法(Brent method)
補間による探索を行うための条件を追加したのが, このブレント法である. 条件とは, 現在の探索点と補間による新しい探索点の幅が前の探索時の更新幅の $\frac{1}{2}$ を下回ってなければ補間による探索を行わないというものである. つまり, 二分法を用いた探索幅の更新よりもより早いスピードで探索幅を小さくすることを要求するものであり, これを満たさない場合は二分法による探索点が採用される[6][Brent, 1973, Algorighms for Minimization without Derivatives].
なお, 補間は2点を用いる線形補間だけでなく, 3点を用いる逆二次補間を導入している. 3点を用いる補間としては放物線補間も考えられるが, これは任意の2点間で関数が単一の値を持たない場合の精度が悪いため推奨されていない. ちなみに逆補間とは, 標本点 $(x_i, y_i) ,,(i = 1, \ldots, N)$ に対して, $f(x_i) = y_i$ を満たす関数から, $g(y_i) = x_i$ を満たす関数を見つけることである.
標本点 $(x_{n-2}, f_{n-2}), (x_{n-1}, f_{n-1}), (x_{n}, f_{n})$ が与えられたときに, $f(x) = 0$ を満たす $x$ は逆二次補間を用いると, 次のように予測される.

input: function f
input: point a, b such that f(a)f(b) < 0 and |f(b)| < |f(a)|
constant: epsilon 許容誤差
constant: delta 計算機イプシロン
c = a
e = d = b - a
while |f(b)| > epsilon:
alpha = 0.5*(a - b)
beta = f(b) / f(c)
if |e| < delta or |f(c)| < |f(b)|: # 二分法
d = e = alpha
else:
if a == c: # 線形補間
p = 2 * alpha * beta
q = 1 - beta
else: # 逆2次補間
q = f(c) / f(a)
r = f(b) / f(a)
p = beta * (2 * alpha * q * (q - r) - (b - c) * (r - 1))
q = (q - 1) * (r - 1) * (beta - 1)
beta, e = e, d
if |2 * p| < |3 * alpha * q| and |p| < |0.5 * beta * q|:
d = - p / q
else: # 二分法
d = e = alpha
if |d| > delta:
s = b + d
elif alpha > 0:
s = b + delta
else:
s = b - delta
c, b = b, s
if f(b)*f(a) > 0:
a = c
d = e = b - c
if |f(a)| < |f(b)|:
a, b, c = b, c, b
return b
擬似コード中$delta$はrelative machine precision(計算機イプシロン)を使用する7.
擬似コード24行目のif文はオーバーフローを監視するものである.
なお, Wikipediaのブレント法のページには, これとは形が違う擬似コードが載せられているが, ブレント本人のアルゴリズムと同値であるか筆者=私はまだ確認できていない.
これは, $f(x) = (x+3)(x-1)^2$ という関数で, $a = -4, b = 0.5, epsilon = 0.01$として, 二分法を実行した結果である.
関数がリプシッツ連続性を有していれば, ブレント法による収束次数は1.61...(黄金比)となる.
まとめ
様々な求根アルゴリズムを紹介してきましたが, それぞれの原理から, そのアルゴリズムが得意な関数と不得意な関数が存在します. 「NUMERICAL RECIPES in C」では導関数が計算不可能な場合はブレント法が推奨されていますが, ある程度関数の形や導関数などが推定できる場合は, それに応じてアルゴリズムを使い分けることでより効率的に探索が行えると思います.
参考
[1] https://ja.wikipedia.org/wiki/二分法
[2] https://en.wikipedia.org/wiki/Secant_method
[3] https://nagahara-masaaki.github.io/assets/pdfs/lecture5.pdf
[4] https://en.wikipedia.org/wiki/False_position_method
[5] Dekker, Theodorus Jozef. "Finding a zero by means of successive linear interpolation." Constructive aspects of the fundamental theorem of algebra (1969): 37-51.
[6] Brent, Richard P. Algorithms for minimization without derivatives. Courier Corporation, 2013.
[7] https://ja.wikipedia.org/wiki/計算機イプシロン