二分法（Pythonで数値計算プログラムを書き直そうシリーズ）

Pythonで数値計算プログラムを書き直そうシリーズ
　「ここ、こうすればいいのに」とかあれば教えてください（土下座）

はじめに

　言わずと知れた二分法（または2分法）なんて、あまり書くことないと思ってましたが、調べると案外書きたい所が出てきました。とりあえず二分法とは、非線型方程式$f(x)=0$を解くための方法です。中間値の定理を応用したアルゴリズムと言えるでしょう。Qiitaで先に詳しく書かれていたのは以下です。導関数を用いた誤差評価の方法があるのとかは知りませんでした。

Python - 非線形方程式解法 二分法 & ニュートン・ラフソン法
2分法の理論と実装
根の探索アルゴリズム

完成したプログラム

bisection.py

#二分法による非線型方程式の解法プログラム
import numpy as np  #数値計算用モジュール
import matplotlib.pyplot as plt  #データ可視化用モジュール


#解きたい方程式
def func_f(x):
    return x**2.0 -2.0


#二分法（方程式の関数項、探索区間の左端、探索区間の右端、誤差範囲、最大反復回数）
def bisection(func_f, x_min, x_max, error=1e-10, max_loop=100):
    #初期値を表示
    num_calc = 0  #計算回数
    print("{:3d}:  {:.15f} <= x <= {:.15f}".format(num_calc, x_min, x_max))

    #中間値の定理の条件を満たすか調べる
    if(0.0 < func_f(x_min)*func_f(x_max)):
        print("error: Section definition is invalid (0.0 < func_f(x_min)*func_f(x_max)).")
        quit()

    #ずっと繰り返す
    while(True):
        #新たな中間値の計算
        x_mid = (x_max +x_min)/2.0

        #探索区間を更新
        if (0.0 < func_f(x_mid)*func_f(x_max)):  #中間と右端の値が同じの時
            x_max = x_mid  #右端を更新
        else:  #中間と左端の値が同じの時
            x_min = x_mid  #左端を更新

        #結果を表示
        num_calc += 1  #計算回数を数える
        print("{:3d}:  {:.15f} <= x <= {:.15f}".format(num_calc, x_min, x_max))

        #「誤差範囲が一定値以下」または「計算回数が一定値以上」ならば終了
        if((x_max-x_min <= error) or max_loop <= num_calc):
            break

    #最終的に得られた解
    print("x = {:.15f}".format(x_mid))

    return x_mid


#可視化（方程式の関数項、グラフ左端、グラフ右端、方程式の解）
def visualization(func_f, x_min, x_max, x_solved):
    plt.xlabel("$x$")  #x軸の名前
    plt.ylabel("$f(x)$")  #y軸の名前
    plt.grid()  #点線の目盛りを表示
    plt.axhline(0, color='#000000')  #f(x)=0の線

    #関数
    exact_x = np.arange(x_min,x_max, (x_max-x_min)/500.0)
    exact_y = func_f(exact_x)

    plt.plot(exact_x,exact_y, label="$f(x)$", color='#ff0000')  #関数を折線グラフで表示
    plt.scatter(x_solved,0.0)  #数値解を点グラフで表示
    plt.text(x_solved,0.0, "$x$ = {:.9f}".format(x_solved), va='bottom', color='#0000ff')
    plt.show()  #グラフを表示


#メイン実行部
if (__name__ == '__main__'):
    #二分法で非線型方程式の解を計算
    solution = bisection(func_f, -2.0, -1.0)

    #結果を可視化
    visualization(func_f, solution-1.0, solution+1.0, solution)

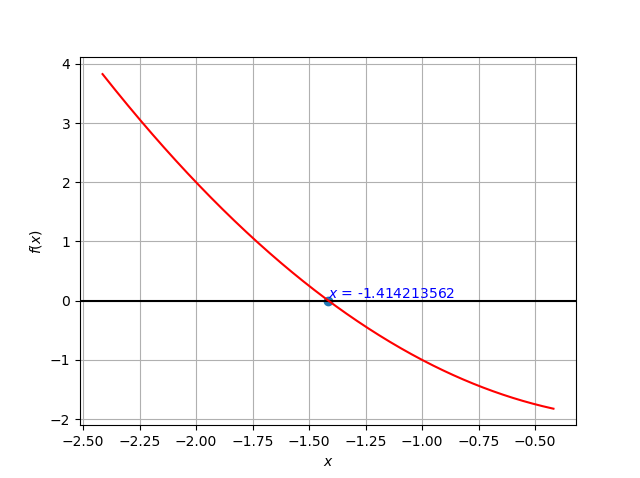
　主なアルゴリズムはbisection関数に書きました。引数として、方程式の関数項$f(x)$、探索区間の左端、探索区間の右端の3つを渡すと、方程式$f(x)=0$の解を「一つだけ」求めます。オプションとして、誤差範囲と最大反復回数も変えることができます。上のプログラムでは$x^2-2=0$の解を、$-2<=x<=-1$の区間で探します。実行すると、計算回数34回目で$-1.41421356238 <= x <= -1.41421356232$と計算されました。$x$の単位がメートルなら、ナノメートルオーダーの値が出ていることになります。実用にも十分耐える精度でしょう。

　個人的にモジュールとして呼び出し可能にしたかったので、そういう構造になっています。モジュールとして使うテストプログラムは以下に書きました。方程式$x^2 -3=0$と、$arctan(x)=0$の解を求めるプログラムになっています。

bisection_test.py

import numpy as np  #数値計算用モジュール
import bisection


def func_f1(x):
    return x**2.0 -3.0

solution1 = bisection.bisection(func_f1, 1.0, 2.0, error=1e-15)
bisection.visualization(func_f1, solution1-1.0, solution1+1.0, solution1)


def func_f2(x):
    return np.arctan(x)

solution2 = bisection.bisection(func_f2, -1.0, 1.0)
bisection.visualization(func_f2, solution2-1.0, solution2+1.0, solution2)

注意すべきと思う点

　細かい話にはなりますが、ちょっとの工夫でこういうトラブルを無くせるのに、という内容を羅列します。ある意味では当たり前の話ばかりなのですが、本とかには載ってないことが多い気がします。

変数名は簡潔で分かりやすい名前にする

　数値計算本を読んでいてイライラしてしまうことの一つ。例えば「区間$x=[a,b]$で$f(x)=0$となる解を探す」という場合、単に変数名をa、b、fと名付けていくと、後でプログラムだけ見た時に何が何だか分からなくなります。区間の範囲で言うと、x1、x2と書くならまだしも、本によってはxn、xpとかで表現していて、どちらが大きい数か分かりません。逆に、コメントも書かなくて済むようにと、やたら長い文章のような変数名を使う人がいますが、数値計算の場合は計算式を書きづらくなるので、かえって不便だと思います。今回はx_min、x_max、func_fなどと名前を付けました。

関数の形は確かめた方がいい

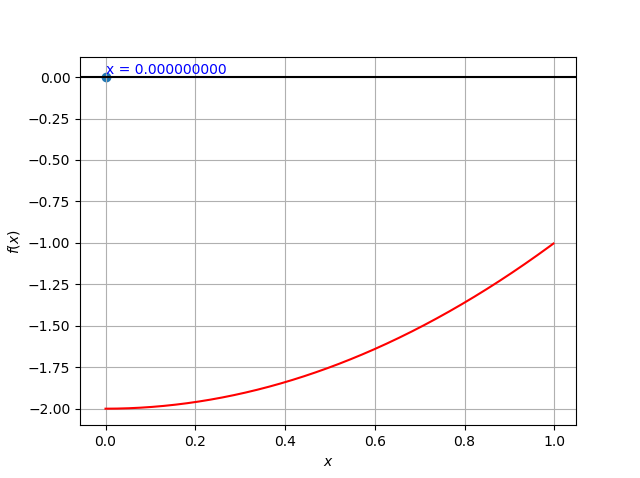
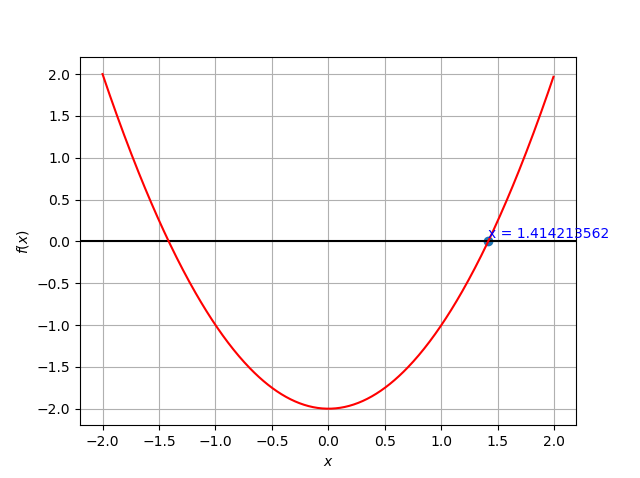
　例えば、方程式$x^2-2=0$の場合、探索区間を$0<=x<=1$とすると間違った解を表示するし、$-2<=x<=2$とすると2つあるうちの片方の解しか求めてくれません（下図を参照）。ちゃんと解が求まっているかは可視化するなりして確かめた方がいいと思います。今回は、Matplotlibで関数と計算結果を表示させました。一つのプログラムで可視化までできてしまうのがPythonのいい所だと思います。

中間値の定理の条件を確認する

　中間値の定理からは、「区間$x=[a,b]$で$f(x)$が連続かつ$f(a)f(b)<0$の時、区間内で$f(x)=0$となる解が一つ以上ある」ことは分かりますが、区間内で$f(x)=0$となる解が「いくつあるか」はすぐには分かりません。プログラム中でまず先に$f(a)f(b)<0$かどうかを判断させることもできますが、それだけでは多項式やsin関数などに対応できないので、根本的な解決にはなりません。
　ただ、コメントでのご指摘もあり、今回のプログラムでは一応「0.0 < func_f(x_min)*func_f(x_max)」を確認するようにしました。これの波及効果として、解の存在しそうな十分広い範囲に対して、相異なる解が2つ以上含まれそうにない十分狭い複数区間で今回のプログラムを使えば、全ての解が求まる可能性が高くなると思われます。

計算回数を考慮した終了条件を入れる

　二分法では大抵、「解の探索区間が誤差範囲を下回るまで繰り返し計算する」ことになりますが、これはwhile文を使って実装されることがほとんどだと思います（たまに誤差範囲を決めずに、for文で適当な回数を反復させてる本もありますが）。しかしこの場合、例えば誤差範囲に$error=e^{-20}$みたいなとてつもなく小さい値を入れると、計算が終わらずに無限ループします。今回は、計算回数が100回を越えたら計算を止めるようにしました。

「中間と右端の関数値の積が正」の時、「右端の値を更新する」ようにする

　何の話だと思われるかもしれませんが、問題の個所は「if (0.0 < func_f(x_mid)*func_f(x_max)):」となっている部分です。これが本によっては、「if (0.0 < func_f(x_mid)):」となっています。つまり、「中間の関数値が正」の時に「右端の値を更新する」となっていることがあります。これだと、右肩上がりの関数には使えますが、右肩下がりの関数では間違った解を計算します。そもそもあまり実用性を求めているプログラムではないですが、汎用性が単純なことでぐっと下がるのは馬鹿らしいので、上のプログラムのように書くべきでしょう。

自作プログラムは使えるのか

　色々書いたけれど、実務的にはライブラリを使った方が早いし、信頼性も高いでしょう。今回扱った二分法と、コメントで教えていただいたBrent法という手法を、SciPyで実装したプログラムを書いておきます。完全に偶然ですが、モジュールの使い方は今回作ったプログラムと似ています。

import scipy.optimize

def func_f1(x):
    return x**2.0 -2.0

#二分法
result1 = scipy.optimize.bisect(func_f1, 1.0, 2.0)
print(result1)

#Brent法
result2 = scipy.optimize.brentq(func_f1, 1.0, 2.0)
print(result2)

　Brent法は二分法の収束が早くなるように工夫した手法だそうです。ニュートン法を知っていると、二分法なんて要らないのではと思うかもしれませんが、ニュートン法には実は大きな欠点があります。二分法では計算できる方程式の解が、ニュートン法では計算できないことがあるのです。それは次の記事で取り上げます。

　ついでに、SymPyを使ったプログラムも書いておきます。たったこれだけで、[-1.41421356237310, 1.41421356237310]と全ての解が表示されます。

　→と、思ったら解けないこともあるようです。解けない時は「No algorithms are implemented to solve equation」と出ます。

import sympy

x = sympy.Symbol("x")
result = sympy.solve(x**2.0 -2.0, x)

print(result)

　ちなみに、線形多項式の方程式を解くにはベアストウ法という手法があり、これは虚数解を含む全ての解を求められる便利な方法です。