C言語で学ぶニュートン法

ニュートン法とは

ニュートン法はある方程式f(x) = 0の実数解を求めるための方法です。例えば$ f(x) = x ^ 3 - 2 $ にすると$ \sqrt[3]{2} $の値を知ることができます。微分を少し使います。

概要

全体的な流れは次のような感じです

1. 初期値$ x_0 $の設定
2. $ n = 0 $とする
3. $ f(x) $の$ x_n $でのを接線求める。方程式は$ y - f(x_n) = f'(x_n) (x - x_n) $になる。
4. 3で求めた接線とy軸との交点を求め、それを$ x_{n+1} $とする。$ 0 - f(x_n) = f'(n_x) (x_{n+1} - x_n) $を$ x_{n+1} $について解くと$ x_{n+1} = - \dfrac{f(x_n)}{f'(x_n)} + x_n $になりますね。
5. $ n := n + 1 $とする。
6. $ |x_{n - 1} - x_n | < 10^{ -6} $なら終了。しなかったなら3.に戻る
   イメージ図は次のような感じです。(http://gijyutsu-keisan.com/science/math/numcal/newton/newton_1.php より引用)
   

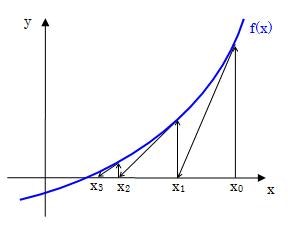
$ f(x) = x ^ 3 - 2 $を例にして考えてみましょう。

1. 初期値は適当に設定してもいいです。ただあんまり変な値にすると収束しません。とりあえず、3にします。
2. $ n = 0 $にします。
3. 接線の方程式は
   $ y - 27 = 27 (x - 3) $
   $ y = 27 x - 54 $
       これが接線の方程式です。
4. 3で求めた接線とy軸との交点は
   $ 0 = 27x - 54 $
   $ x = 2 $
   よって$ x_{n+1} = 2 $になります。
5. $ n = 1 $になります。
6. $ |x_{n - 1} - x_n| = | 3 - 2 | = 1 $なので3に戻ります。

この操作を続けていけば$ x_n = \sqrt[3]{2} $になることはわかるでしょう。

#ソースコード

newton.c

#include <stdio.h>
#include <math.h>

#define EPS (1.0e-6)
#define f(x) (x*x*x-2)
#define df(x) (3*x*x)

int main(){
    double xn, xo; // x_new x_old
    xn = (xo = 2) + 1;
    while(fabs(xn - xo) > EPS){
        xo = xn;
        xn = -1 *f(xo) / df(xo) + xo;
    }
    printf("%f\n%f\n", xn, xn * xn * xn);
}