導入
「施策を打ったら売上が上がった」
「この治療を受けた患者のほうが予後が良い」
「追加授業を受けた学生の成績が高い」
…この手の話は、データがあるほど “それっぽく”見えます。
でも、ここで本当に知りたいのは多くの場合 相関(correlation)ではなく 因果(causality)です。
- 相関:一緒に動く(同時に起きる)
- 因果:介入(やる/やらない)で結果が変わる
因果推論は、ざっくり言うと
「観測データ(実験できない/しにくい状況)から、介入の効果を推定する」
ための考え方・道具箱です。
本記事では、教育・医療・ビジネスに共通する最頻出パターン
“交絡(confounding)”を、ダミーデータで体験しながら腹落ちさせます。
TL;DR
- 「介入した群」と「してない群」をそのまま比べると、交絡で簡単に騙されます。
- 因果推論の第一歩は、何が交絡因子(共通原因)かを言語化し、図(DAG)にすること。
- 評価は「ランダム化比較試験(RCT)」が理想だが、できないときは
調整(回帰/層別)や傾向スコア(propensity score)などで近づけます。 - ただし、未観測の交絡や 重なり(overlap)の欠如 があると限界があります。
0. 3分でわかる:今回扱う登場人物
-
T:介入(Treatment)。例:追加授業を受けた / 治療を受けた / キャンペーンを受けた -
Y:結果(Outcome)。例:テスト点 / 予後 / 購入額 -
X:交絡因子(Confounder)。例:やる気 / 重症度 / もともとの購入意欲
ポイントはここです:
X が T にも Y にも効く(共通原因)と、
「TしたからYが上がった」と見えても、実は X のせいかもしれない。
1. まずは図にする(DAG:因果関係の簡略図)
今回の最小パターンはこれです(超重要)。
-
T → Yが「知りたい効果(介入の効果)」 -
X → TとX → Yがあると、単純比較はバイアスを持ちます
2. Google Colabで体験する(コードはコピペでOK)
このデモでは、真の因果効果(tau)を こちらが知っているダミーデータを作ります。
そして推定法の違いで、結果がどう変わるかを見ます。
セル1:準備
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.preprocessing import StandardScaler
SEED = 42
rng = np.random.default_rng(SEED)
os.makedirs("fig", exist_ok=True)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
セル2:ダミーデータ生成(交絡あり)
def simulate(n=3000, tau=5.0, a=1.5, b=3.0, noise=1.0, seed=0):
"""
X: 交絡因子
T: Xが大きいほど介入されやすい(例: やる気があるほど追加授業を受ける)
Y: 本当は tau*T の効果があるが、XもYに強く効く
"""
rng = np.random.default_rng(seed)
X = rng.normal(0, 1, n)
p = sigmoid(a * X) # 介入確率(傾向スコアの真値に近いもの)
T = rng.binomial(1, p, n)
Y = tau * T + b * X + rng.normal(0, noise, n)
return pd.DataFrame({"X": X, "T": T, "Y": Y, "p_true": p})
tau_true = 5.0
df = simulate(tau=tau_true, seed=SEED)
df.head(), df["T"].mean()
セル3:図1「介入群と非介入群で、Xが違う」=交絡の可視化
plt.figure(figsize=(7.2,4.2))
plt.hist(df.loc[df["T"]==0, "X"], bins=40, alpha=0.7, label="T=0 (control)")
plt.hist(df.loc[df["T"]==1, "X"], bins=40, alpha=0.7, label="T=1 (treated)")
plt.title("Confounding check: X distribution differs between treated/control")
plt.xlabel("Confounder X")
plt.ylabel("count")
plt.legend()
plt.tight_layout()
plt.savefig("fig/fig1_x_by_t.png", dpi=160, bbox_inches="tight")
plt.show()
print("Saved: fig/fig1_x_by_t.png")
セル4:図2「単純比較(naive)」はズレる
ate_naive = df.loc[df["T"]==1, "Y"].mean() - df.loc[df["T"]==0, "Y"].mean()
print("True ATE (tau) =", tau_true)
print("Naive diff-in-means =", ate_naive)
plt.figure(figsize=(6.2,4.2))
means = [df.loc[df["T"]==0, "Y"].mean(), df.loc[df["T"]==1, "Y"].mean()]
plt.bar(["T=0", "T=1"], means)
plt.title("Naive comparison of Y (biased under confounding)")
plt.ylabel("mean(Y)")
plt.tight_layout()
plt.savefig("fig/fig2_naive_means.png", dpi=160, bbox_inches="tight")
plt.show()
print("Saved: fig/fig2_naive_means.png")
セル5:回帰で調整(Y ~ T + X)=“Xを揃えて比べる”
X_reg = df[["T", "X"]].values
y_reg = df["Y"].values
lr = LinearRegression().fit(X_reg, y_reg)
tau_reg = lr.coef_[0]
print("Regression-adjusted estimate (coef of T) =", tau_reg)
セル6:傾向スコア(propensity score)で調整(IPW / AIPW)
傾向スコアは「その人(そのサンプル)が介入されやすい確率」です。
ここではロジスティック回帰で T ~ X を学習して推定します。
# 1) 傾向スコア推定 p_hat = P(T=1|X)
clf_ps = LogisticRegression(max_iter=500)
X_ps = df[["X"]].values
T_ps = df["T"].values
clf_ps.fit(X_ps, T_ps)
p_hat = clf_ps.predict_proba(X_ps)[:,1]
# クリップ(極端な重みを避けるための現場的安全策)
eps = 1e-3
p_hat = np.clip(p_hat, eps, 1-eps)
df["p_hat"] = p_hat
# 2) 図3:overlap(重なり)チェック
plt.figure(figsize=(7.2,4.2))
plt.hist(df.loc[df["T"]==0, "p_hat"], bins=40, alpha=0.7, label="T=0")
plt.hist(df.loc[df["T"]==1, "p_hat"], bins=40, alpha=0.7, label="T=1")
plt.title("Propensity score overlap (positivity check)")
plt.xlabel("p_hat = P(T=1|X)")
plt.ylabel("count")
plt.legend()
plt.tight_layout()
plt.savefig("fig/fig3_ps_overlap.png", dpi=160, bbox_inches="tight")
plt.show()
print("Saved: fig/fig3_ps_overlap.png")
# 3) IPW(Inverse Probability Weighting)
Y = df["Y"].values
T = df["T"].values
ipw = (T*Y/df["p_hat"].values) - ((1-T)*Y/(1-df["p_hat"].values))
ate_ipw = ipw.mean()
# 4) AIPW(Augmented IPW / doubly robust)
# outcome models: E[Y|T=1,X], E[Y|T=0,X]
lr1 = LinearRegression().fit(df.loc[df["T"]==1, ["X"]].values, df.loc[df["T"]==1, "Y"].values)
lr0 = LinearRegression().fit(df.loc[df["T"]==0, ["X"]].values, df.loc[df["T"]==0, "Y"].values)
mu1 = lr1.predict(df[["X"]].values)
mu0 = lr0.predict(df[["X"]].values)
aipw = (mu1 - mu0) + T*(Y - mu1)/df["p_hat"].values - (1-T)*(Y - mu0)/(1-df["p_hat"].values)
ate_aipw = aipw.mean()
print("ATE naive =", ate_naive)
print("ATE regression adj =", tau_reg)
print("ATE IPW =", ate_ipw)
print("ATE AIPW =", ate_aipw)
セル7:図4 推定値まとめ(真の効果と並べる)
methods = ["True", "Naive", "RegAdj", "IPW", "AIPW"]
vals = [tau_true, ate_naive, tau_reg, ate_ipw, ate_aipw]
plt.figure(figsize=(7.2,4.2))
plt.bar(methods, vals)
plt.axhline(tau_true, linestyle="--", label="true tau")
plt.title("Causal effect estimates (toy demo)")
plt.ylabel("Estimated ATE")
plt.legend()
plt.tight_layout()
plt.savefig("fig/fig4_estimates.png", dpi=160, bbox_inches="tight")
plt.show()
print("Saved: fig/fig4_estimates.png")
セル8:交絡が強すぎてoverlapが崩れるとどうなる?
「介入される人がほぼ固定」になると、因果効果の推定は不安定になります。
(教育なら“やる気が極端に高い人しか受講しない”、医療なら“重症しか治療されない”、ビジネスなら“購入確率が高い人だけ配信される”など)
df_bad = simulate(tau=tau_true, a=4.0, seed=SEED) # aを大きくして介入が偏る
# 傾向スコア推定
clf_ps.fit(df_bad[["X"]].values, df_bad["T"].values)
p_bad = np.clip(clf_ps.predict_proba(df_bad[["X"]].values)[:,1], eps, 1-eps)
df_bad["p_hat"] = p_bad
plt.figure(figsize=(7.2,4.2))
plt.hist(df_bad.loc[df_bad["T"]==0, "p_hat"], bins=40, alpha=0.7, label="T=0")
plt.hist(df_bad.loc[df_bad["T"]==1, "p_hat"], bins=40, alpha=0.7, label="T=1")
plt.title("Overlap becomes poor when treatment assignment is too deterministic")
plt.xlabel("p_hat")
plt.ylabel("count")
plt.legend()
plt.tight_layout()
plt.savefig("fig/fig5_overlap_bad.png", dpi=160, bbox_inches="tight")
plt.show()
print("Saved: fig/fig5_overlap_bad.png")
3. 実行結果の図
図1:交絡チェック(Xの分布がTで違う)
図2:単純比較(naive)はズレる
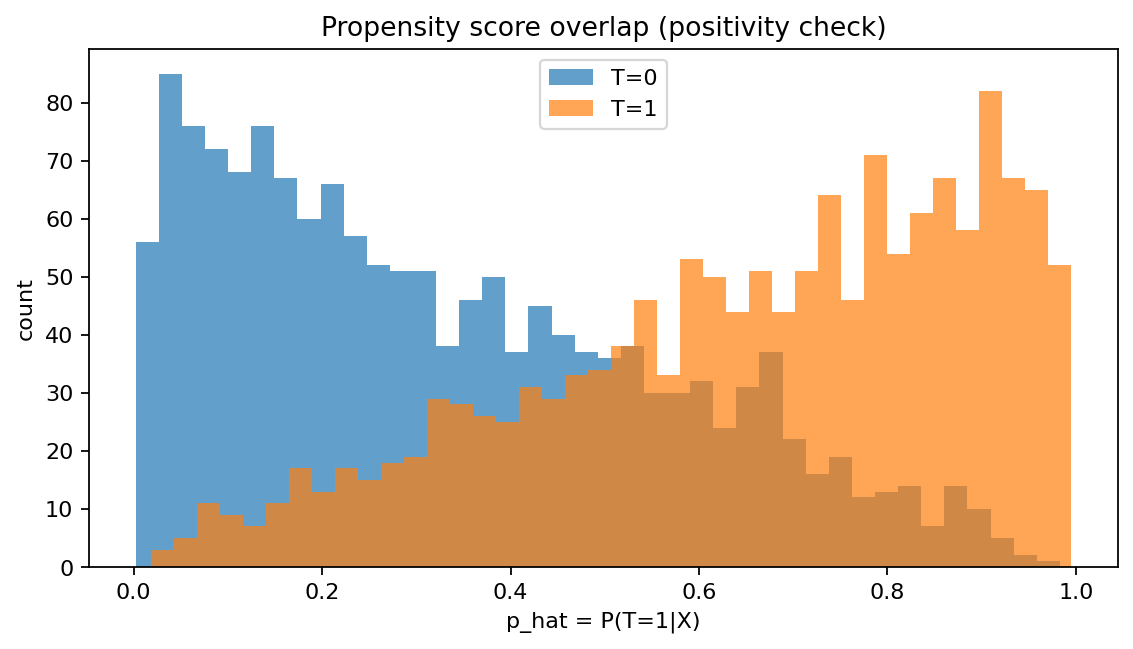
図3:傾向スコアの重なり(overlap)チェック
図4:推定法の比較(True/Naive/RegAdj/IPW/AIPW)
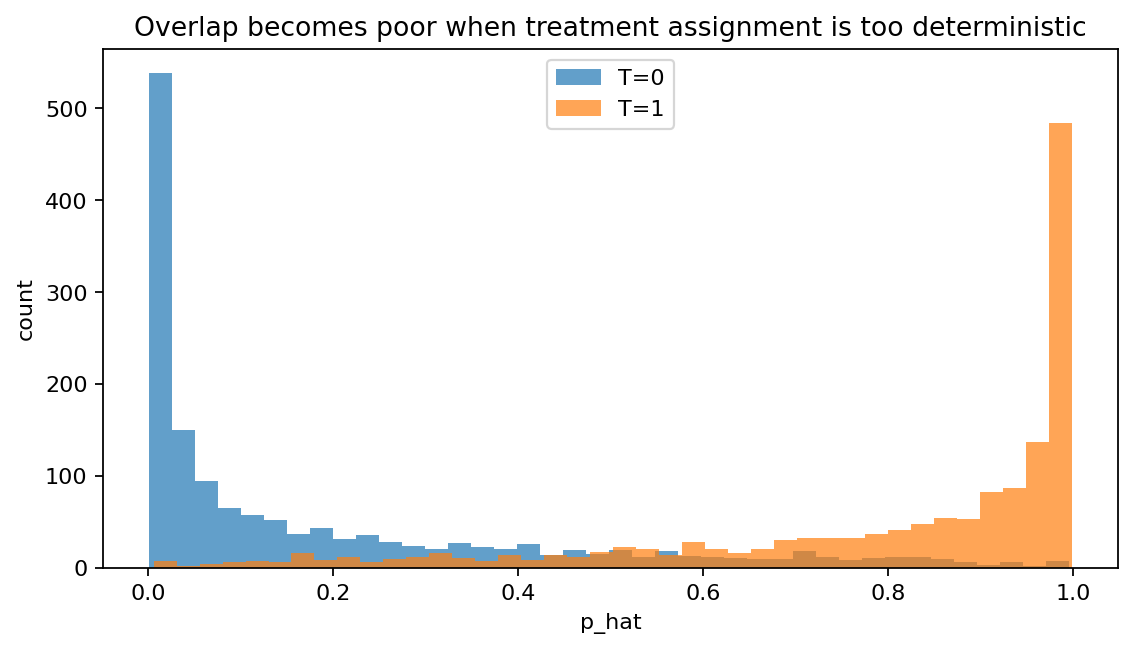
図5:overlapが崩れた例
4. 図の読み方
このデモは「交絡がある観測データで、因果効果をどう推定するか」を最小構成で体験するためのものです。ここでは、生成過程で 真の因果効果(true tau)= 5 を埋め込んでいます(現実データでは真値は分かりません)。
4.1 交絡(confounding)
図1では、T=0(control)とT=1(treated)で、交絡因子Xの分布が明確に異なっています。
具体的には、treated側(オレンジ)が Xの大きい方向に寄っているため、
- そもそも「条件の違う集団」を比較してしまっている
- Yの差には「処置の効果」だけでなく「Xの違い」も混ざる
という状況です。これが 交絡(confounding) です。
図2は、単純に E[Y|T=1] - E[Y|T=0] を見たものです。
今回の実行では、素朴比較は真の効果(5)より大きく見積もられています(おおよそ8程度)。
これは「処置の効果が本当に大きい」のではなく、
- treated側は X が大きめ
- そして Y は X にも依存する
という生成過程のため、Xの影響が混ざってY差が水増しされるからです。
このズレを 交絡バイアス と呼びます。
4.2 ATE(平均介入効果)
ATE は「全体として、介入したら平均でどれくらい変わるか」です。
(教育なら平均点がどれくらい上がるか、医療なら平均でどれくらい改善するか…)
4.3 調整(adjustment)
回帰調整(RegAdj)は「Xを揃えてTの差を見る」ことに相当します。
ただし回帰はモデル仮定(線形性など)に依存します。
4.4 傾向スコア(propensity score)と overlap(positivity)
- 傾向スコア
p_hat = P(T=1|X)は「介入されやすさ」 - overlap(重なり)がある=介入/非介入の両方が起こり得る領域が存在する
因果推論の多くの手法は、treatedとcontrolが「同じようなXの個体」をある程度共有していること(overlap / positivity)を暗に必要とします。
図3では、T=0は p_hat(処置を受ける確率)が低め、T=1は高めに偏っていますが、0.3〜0.7付近には重なりがあり、最低限のoverlapはあります。
ここが完全に分離して p_hat≈0 と p_hat≈1 ばかりになると、IPWの重みが極端になり、推定が不安定になります(→図5)。
4.5 IPW と AIPW(doubly robust)
- IPW:介入されやすい人に小さな重み、されにくい人に大きな重みをつけて“疑似的にランダム化”に近づける
-
AIPW:IPWに、結果モデル(mu1, mu0)も併用する“保険付き”推定
直感としては「重み付けだけの弱点」も「回帰だけの弱点」も両方緩和しやすい
図4では、各推定量のATE(平均処置効果)の比較をしています。
- Naive:交絡のため大きくズレる
- RegAdj(回帰調整):Xを条件づけて差を見に行くので、真値付近へ戻る
- IPW(逆確率重み付け):処置の偏りを重みで補正し、真値付近へ戻る
- AIPW(Augmented IPW):回帰調整とIPWを組み合わせ、より安定しやすい
特にAIPWは「どちらか片方(傾向スコアモデル or outcomeモデル)が正しければ」うまくいく性質(※直感的には“保険”)を持ち、実務で好まれる理由の一つです。
ただし現実データでは真値(true tau)が分からないため、推定値が「正しそうか」は、前提チェック(overlapなど)や感度分析、ドメイン知識とセットで判断します。
図5は、処置の割り当てがXでほぼ決まってしまう(p_hatが0か1に張り付く)状況を作っています。
この場合は、treatedとcontrolがほとんど重ならないため、
- 「似た個体どうしの比較」ができない
- 重みが極端になって推定が不安定になる
という問題が起きます。これは 推定器のテクニックで簡単に解決できる問題ではなく、データの情報不足に近いです。
実務では、次のような対処が検討されます。
- overlapのある範囲に母集団を限定する(trimming / 共通サポート)
- そもそも設計(割付や収集)を見直す(実験、準実験、追加データ)
- 推定したい効果(母集団・対象)を定義し直す
5. 教育・医療・ビジネスへの横展開(同じ構造で考える)
5.1 教育(例:追加授業の効果)
- T:追加授業を受けた
- Y:期末テスト点
- X:やる気、基礎学力、家庭環境
- 落とし穴:やる気がある学生ほど受講しがち → 単純比較はバイアス
5.2 医療(例:治療の効果)
- T:新薬を投与
- Y:予後指標
- X:重症度、併存疾患、年齢
- 落とし穴:重症ほど治療される/されない → 比較が難しい
:::note warn
医療での因果推論は、倫理・安全・規制の観点からも慎重に。
本記事は方法の直感理解のためのデモで、医療判断を目的としません。
:::
5.3 ビジネス(例:キャンペーン配信の効果)
- T:クーポン配布
- Y:購入額/継続率
- X:過去購買、閲覧、会員ランク
- 落とし穴:買いそうな人に配るほど効果が高く見える(選別バイアス)
6. 実務・研究でのチェックリスト(最初にこれだけやる)
- 介入 T / 結果 Y / 交絡 X を言語化する(メタデータ重要)
- DAG(因果の簡略図)を書く
- 「何を推定したいか」(ATE/特定集団での効果など)を決める
- overlap(重なり)を確認する(図3のようなチェック)
- 推定法を複数試す(回帰、IPW、AIPWなど)
- 限界を明記する:未観測交絡、測定誤差、介入の定義の揺れ など
まとめ
因果推論は「難しい数式の世界」ではなく、まずは
- 相関と因果を区別する
- 交絡を疑う
- 比較できる状態に近づける(調整/重み付け)
- 前提(overlapや未観測交絡)を点検する
という“運用の型”として非常に強力です。
まずは本記事のダミーデータを動かして、
「単純比較がどれだけ簡単に騙されるか」を体験してみてください。
- 交絡があると素朴比較はズレる(図1→図2)
- 傾向スコアのoverlap確認は必須(図3)
- 調整すると真値に近づけるが、前提が崩れると推定は苦しい(図4→図5)