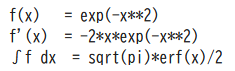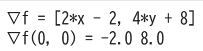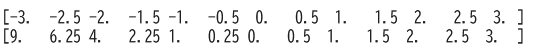この記事では、前回触れた
sympy の式 → NumPy / SciPy で数値計算
をつなぐ重要な部品である sympy.lambdify を、もう少し丁寧に掘り下げます。
- 「授業では sympy で式を扱いたい」
- 「研究では NumPy / SciPy で数値計算を回したい」
- 「同じモデルを、紙の数式とコードで二重管理したくない」
といった場面で、lambdify は非常に有用です。
1. lambdify とは何か
公式ドキュメント風に一言で書けば、
sympy の記号式(Symbolic Expression)から、Python の数値関数を生成する関数
です。
import sympy as sp
x = sp.symbols('x')
expr = sp.sin(x) * sp.exp(-x / 5)
f = sp.lambdify(x, expr, modules="numpy")
ここで f は
def f(x):
# NumPy(あるいは math 等)の関数を使って expr を評価する関数
...
に相当する「普通の Python 関数」になります。
NumPy の配列でも、Python の float でもそのまま評価できます。
この「数式として書いたモデルを、そのまま数値計算の関数に変換できる」という点が、授業や研究での再利用性を大きく高めてくれます。
2. 単変数関数の最小例
まずは最小限の例から。
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
# 記号変数と式
x = sp.symbols('x')
f_sym = sp.sin(x) * sp.exp(-x / 5)
# lambdify で NumPy 用の関数に変換
f = sp.lambdify(x, f_sym, modules="numpy")
# 数値評価&プロット
xs = np.linspace(0, 20, 400)
ys = f(xs) # NumPy 配列をそのまま渡せる
plt.plot(xs, ys)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.title("sympy → NumPy への橋渡し")
plt.grid(True)
plt.show()
ポイントは次の 3 つです。
- 数式の定義は sympy で
- 数値評価と可視化は NumPy / Matplotlib で
- その間の橋渡しを
lambdifyが肩代わりしてくれる
これだけでも「数式で考えたモデルを、そのままコードに落とす」感覚を学生に示せます。
3. 微分・積分・極限を含めて lambdify する
sympy で解析的に微分・積分した結果を、そのまま数値評価に回すことも簡単です。
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
x = sp.symbols('x')
f_sym = sp.exp(-x**2)
# 解析的な微分・積分
df_sym = sp.diff(f_sym, x)
F_sym = sp.integrate(f_sym, x)
print("f(x) =", f_sym)
print("f'(x) =", df_sym)
print("∫f dx =", F_sym)
# 数値評価用に変換
f = sp.lambdify(x, f_sym, modules="numpy")
df = sp.lambdify(x, df_sym, modules="numpy")
F = sp.lambdify(x, F_sym, modules="numpy")
xs = np.linspace(-3, 3, 400)
F_vec = np.vectorize(F)
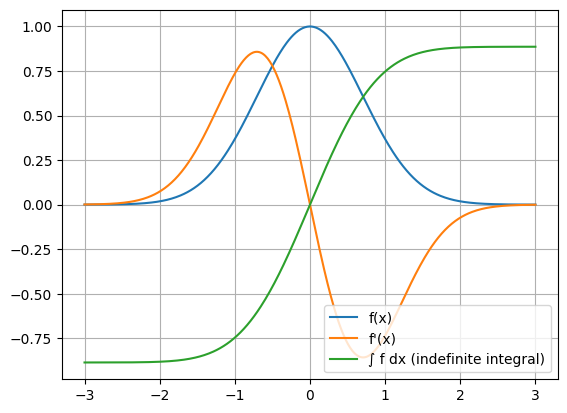
plt.plot(xs, f(xs), label="f(x)")
plt.plot(xs, df(xs), label="f'(x)")
plt.plot(xs, F_vec(xs), label="∫ f dx (indefinite integral)")
plt.legend()
plt.grid(True)
plt.show()
授業であれば、
- 手計算で微分・積分した結果と sympy が出す式の比較
- さらにそのグラフを重ねて視覚的に確認
という一連の流れを 1 つの Notebook にまとめて提示できます。
4. 複数変数・パラメータを含む場合
次は複数変数を含む場合です。例として、簡単な 2 変数関数
$$
f(x, y) = \exp\left(-\frac{x^2 + y^2}{2\sigma^2}\right)
$$
を考えます。
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
x, y, sigma = sp.symbols('x y sigma', positive=True)
f_sym = sp.exp(-(x**2 + y**2) / (2 * sigma**2))
# (x, y, sigma) → f(x, y, sigma)
f = sp.lambdify((x, y, sigma), f_sym, modules="numpy")
# 数値パラメータを決めて、2次元グリッド上で評価
xs = np.linspace(-3, 3, 201)
ys = np.linspace(-3, 3, 201)
X, Y = np.meshgrid(xs, ys)
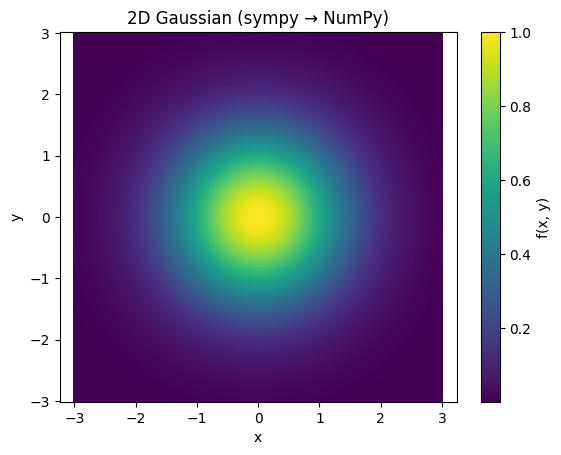
Z = f(X, Y, 1.0) # sigma = 1
plt.pcolormesh(X, Y, Z, shading="auto")
plt.colorbar(label="f(x, y)")
plt.xlabel("x")
plt.ylabel("y")
plt.title("2D Gaussian (sympy → NumPy)")
plt.axis("equal")
plt.show()
ここでのポイント:
-
lambdifyの第 1 引数は タプル(x, y, sigma)にしておく - 生成された
fはf(X, Y, 1.0)のように 複数引数を取る関数になる - パラメータ(ここでは
sigma)をそのまま引数として渡せるので、
演習で「σ を変えてグラフを観察せよ」といった課題にも使いやすいです
5. ベクトル値関数:勾配やヤコビアンをまとめて lambdify
最適化問題や数値解法では、スカラー値関数だけでなく ベクトル値関数(勾配・ヤコビアン)を扱うことも多いです。
例として、2変数関数
$$
f(x, y) = (x - 1)^2 + 2(y + 2)^2
$$
の勾配 $\nabla f$ を lambdify してみます。
import sympy as sp
import numpy as np
x, y = sp.symbols('x y')
f_sym = (x - 1)**2 + 2*(y + 2)**2
# 勾配ベクトル
grad_f_sym = [sp.diff(f_sym, v) for v in (x, y)]
print("∇f =", grad_f_sym)
# (x, y) → (df/dx, df/dy)
grad_f = sp.lambdify((x, y), grad_f_sym, modules="numpy")
# 例として (x, y) = (0, 0) で評価
gx, gy = grad_f(0.0, 0.0)
print("∇f(0, 0) =", gx, gy)
grad_f_sym をリスト(あるいは sp.Matrix)にしておくと、lambdify は
- Python のリスト
- あるいは NumPy 配列
として返してくれます。
SciPy の最適化ルーチンに勾配を渡したい場合などに、そのまま再利用できます。
6. SciPy と組み合わせる:積分・最適化
6.1 sympy でモデル → SciPy で数値積分
先ほどのガウス関数を例に、sympy で式を定義し、SciPy の数値積分で評価してみます。
import sympy as sp
import numpy as np
from scipy import integrate
# 記号式の定義
x, a = sp.symbols('x a', positive=True)
f_sym = sp.exp(-a * x**2)
# lambdify: (x, a) → f(x, a)
f = sp.lambdify((x, a), f_sym, modules="numpy")
# SciPy の quad で ∫_0^∞ exp(-a x^2) dx を評価
def integral(a_value: float) -> float:
func = lambda t: f(t, a_value)
val, _ = integrate.quad(func, 0, np.inf)
return val
for a_val in [0.5, 1.0, 2.0]:
print(f"a = {a_val:3.1f}, integral ≈ {integral(a_val):.6f}")
ここでは、
- 式そのものは sympy で定義
- 数値積分の処理は SciPy に任せる
という役割分担になっています。
教科書に載っているような「パラメータ付きの積分公式」を、数値的に確かめる演習にも使えます。
6.2 sympy で勾配 → SciPy で最適化
SciPy の最適化ルーチン scipy.optimize.minimize では、目的関数だけでなく勾配も渡せます。
これも lambdify で簡単に用意できます。
import sympy as sp
import numpy as np
from scipy import optimize
# 目的関数
x1, x2 = sp.symbols('x1 x2')
f_sym = (x1 - 1)**2 + 2*(x2 + 2)**2
# 勾配
grad_sym = [sp.diff(f_sym, v) for v in (x1, x2)]
# lambdify で数値関数化
f = sp.lambdify((x1, x2), f_sym, modules="numpy")
grad = sp.lambdify((x1, x2), grad_sym, modules="numpy")
def f_wrapper(xs: np.ndarray) -> float:
return float(f(xs[0], xs[1]))
def grad_wrapper(xs: np.ndarray) -> np.ndarray:
gx, gy = grad(xs[0], xs[1])
return np.array([gx, gy], dtype=float)
x0 = np.array([0.0, 0.0])
res = optimize.minimize(f_wrapper, x0, jac=grad_wrapper)
print("最適解:", res.x)
print("f(最適解) =", res.fun)
- sympy 上の計算と、SciPy の最適化ルーチンが 同じモデル定義を共有する
- パラメータが増えても、微分の計算そのものは sympy に任せてしまえる
ため、実験用のモデルを頻繁に変更するプロジェクトでは非常に助かります。
7. ODE の数値解と lambdify:SciPy solve_ivp との連携
よくあるパターンとして、
- sympy で ODE の右辺を記号式として書く
- lambdify で数値関数に変換
- SciPy の
solve_ivpで数値解を求める
という流れがあります。
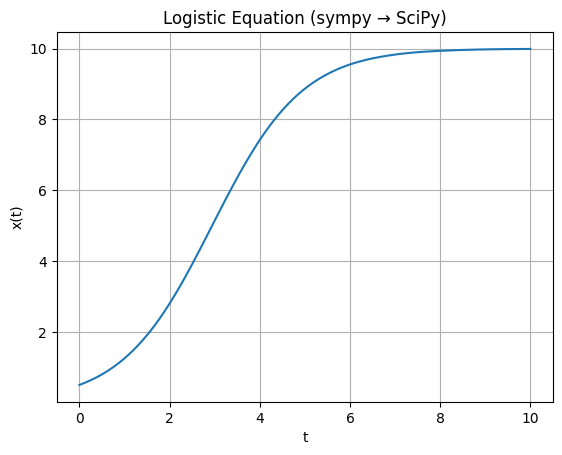
例として、ロジスティック方程式
$$
\frac{dx}{dt} = r x (1 - x/K)
$$
を考えます。
import sympy as sp
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
# 記号式で ODE を定義
t = sp.symbols('t')
x = sp.Function('x')(t)
r, K = sp.symbols('r K', positive=True)
dxdt_sym = r * x * (1 - x / K)
# lambdify: (t, x, r, K) → dx/dt
dxdt = sp.lambdify((t, x, r, K), dxdt_sym, modules="numpy")
def rhs(t: float, y: np.ndarray, r_val: float, K_val: float) -> np.ndarray:
return np.array(dxdt(t, y[0], r_val, K_val), dtype=float)
r_val = 1.0
K_val = 10.0
t_span = (0.0, 10.0)
t_eval = np.linspace(*t_span, 400)
y0 = [0.5]
sol = solve_ivp(rhs, t_span, y0, args=(r_val, K_val), t_eval=t_eval)
plt.plot(sol.t, sol.y[0])
plt.xlabel("t")
plt.ylabel("x(t)")
plt.title("Logistic Equation (sympy → SciPy)")
plt.grid(True)
plt.show()
この例では、
- ODE のモデルは sympy で書き、
- 数値解法の部分は SciPy にまかせる
という明確な分離ができます。
解析解が求まる ODE であれば、sympy の dsolve と数値解を比較する演習も容易です。
8. modules オプションの使い分け
lambdify の第 3 引数 modules は、どの数値ライブラリを使うかを指定するオプションです。
よく使うのは次のあたりです。
-
"numpy"- 最も一般的。配列演算を活用したい場合はこれで十分なことが多いです。
-
"math"- 純粋に Python の
mathモジュールを使う。
配列ではなくスカラーだけ扱う関数にしたい場合など。
- 純粋に Python の
-
["numpy", "math"]- NumPy に無い関数は
mathにフォールバックさせたい、といった場合。
- NumPy に無い関数は
例:
import sympy as sp
import numpy as np
x = sp.symbols('x')
f_sym = sp.log(1 + x**2)
# NumPy 版
f_np = sp.lambdify(x, f_sym, modules="numpy")
# math 版(配列はそのまま渡せない)
f_math = sp.lambdify(x, f_sym, modules="math")
print(f_np(np.array([0.0, 1.0, 2.0])))
print(f_math(0.5))
授業では、
- 「配列で扱いたいときは NumPy」
- 「スカラーだけなら math でもよい」
といった切り分けを示すと、学生が混乱しにくくなります。
9. よくあるハマりどころ
9.1 スカラー vs 配列
modules="numpy" で作った関数は、float も配列も受け付けますが、
SciPy の一部関数は「スカラー専用」「配列を返してはいけない」といった制約を持ちます。
- 例:
integrate.quadはスカラー返り値を期待 - 例:
solve_ivpの右辺は 1 次元配列を返す必要がある
その場合は、wrapper 関数を一枚かませて
def f_scalar(x):
return float(f(x)) # 必ず float にキャスト
のようにしておくと安全です。
9.2 Piecewise を含む式
分岐を含む関数を sp.Piecewise で定義した場合、
そのまま modules="numpy" で lambdify すると、内部で numpy.where などを使った関数を生成してくれます。
import sympy as sp
import numpy as np
x = sp.symbols('x')
f_sym = sp.Piecewise(
(x**2, x < 0),
(x, True)
)
f = sp.lambdify(x, f_sym, modules="numpy")
xs = np.linspace(-3, 3, 13)
print(xs)
print(f(xs))
ただし、条件式に and / or を直接書くのではなく、
(x < 0) & (x > -1) のように ビット演算子(&, |)を使う必要がある点には注意が必要です。
10. 授業・演習での利用アイディア
最後に、lambdify を絡めた演習や授業ネタの例を挙げておきます。
- 微分積分学:
- sympy で導関数・不定積分を出し、lambdify → 数値プロット
- 解析解と数値積分(SciPy)の比較
- 線形代数:
- 固有値問題の記号計算 → 固有ベクトルを lambdify → 数値評価
- 常微分方程式:
- 解析解(
dsolve) vs 数値解(solve_ivp)を同じモデルから生成
- 解析解(
- 数値解析:
- Newton 法などの反復法を自作する際、勾配・ヘッセ行列を sympy + lambdify で生成
- 実験データ解析:
- モデル関数を sympy で書き、lambdify した関数を SciPy のフィッティングルーチンに渡す
共通しているのは、
「数式としてのモデル定義」と「数値計算としての実装」を分離しつつ、一貫性を保つ
という設計思想です。
lambdify は、その橋渡しを担う小さな関数ですが、
教育・研究の現場では驚くほど多くの場面で役立ちます。
まとめ
本記事では、
-
lambdifyの基本的な使い方 - 複数変数・ベクトル値関数・パラメータ付き関数への拡張
- SciPy(積分・最適化・ODE)との連携
-
modulesオプションや、ありがちなハマりどころ
といった点をざっと整理しました。
sympy でモデルの式を記述し、lambdify で NumPy / SciPy に橋渡しするワークフローに慣れておくと、
授業・演習・研究・趣味の数値実験まで、一貫した形で Python を活用しやすくなります。
どこか一部分だけでも、日々の実験コードや演習課題に取り入れてみてもらえれば幸いです。