はじめに
前回の「単一ニューロンは直線分離、2 層で XOR を解ける」という内容を踏まえ、論理回路(加算器)を題材に、2 次元の可視化でニューラルネットの表現力を学びます。
最初に用語を共有します。
- パーセプトロン:入力の重み付き和にしきい値(バイアス)を加え、ステップ関数で 0/1 を出す最小のニューロン。
- 活性化関数:出力の非線形変換。学習では連続な関数(シグモイドや ReLU)をよく使います。
- MLP(多層パーセプトロン):ニューロンを層状に積んだネットワーク。隠れ層に非線形を挟むことで表現力が増します。
- 決定領域:入力平面を、分類器が 0 と 1 に分けた塗り分け領域のこと。
以降、図は(A,B) の 2D 平面に点をプロットし、背景をモデルの識別領域で塗り分けます。全加算器のように 3 入力の場合は、Cin=0 と Cin=1 の2 枚に分けて眺めます。
1. 半加算器:Sum は XOR、Carry は AND
1.1 真理表と式
| A | B | Sum (A⊕B) | Carry (A∧B) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
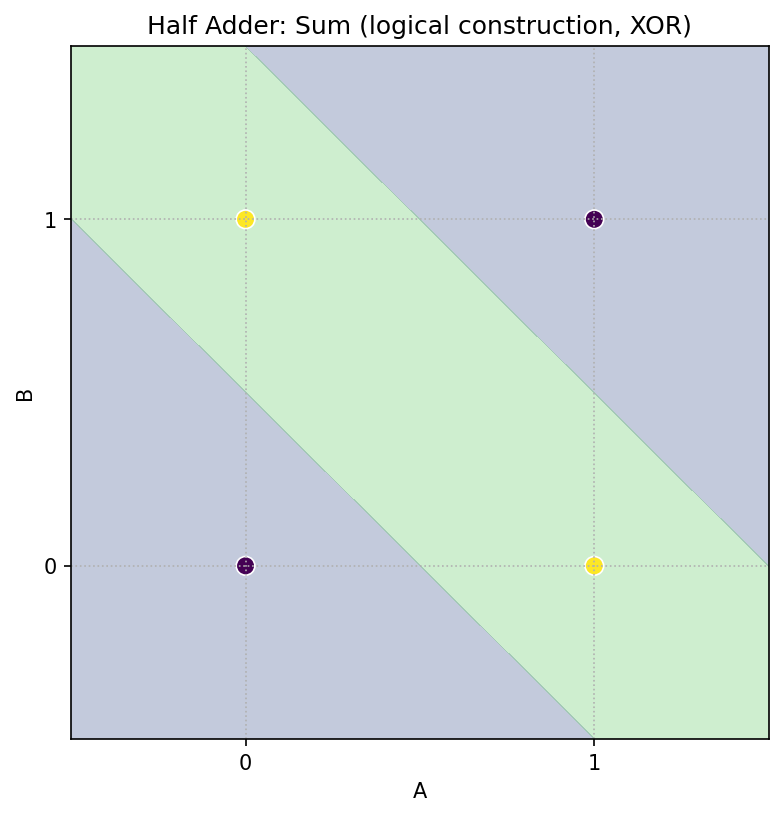
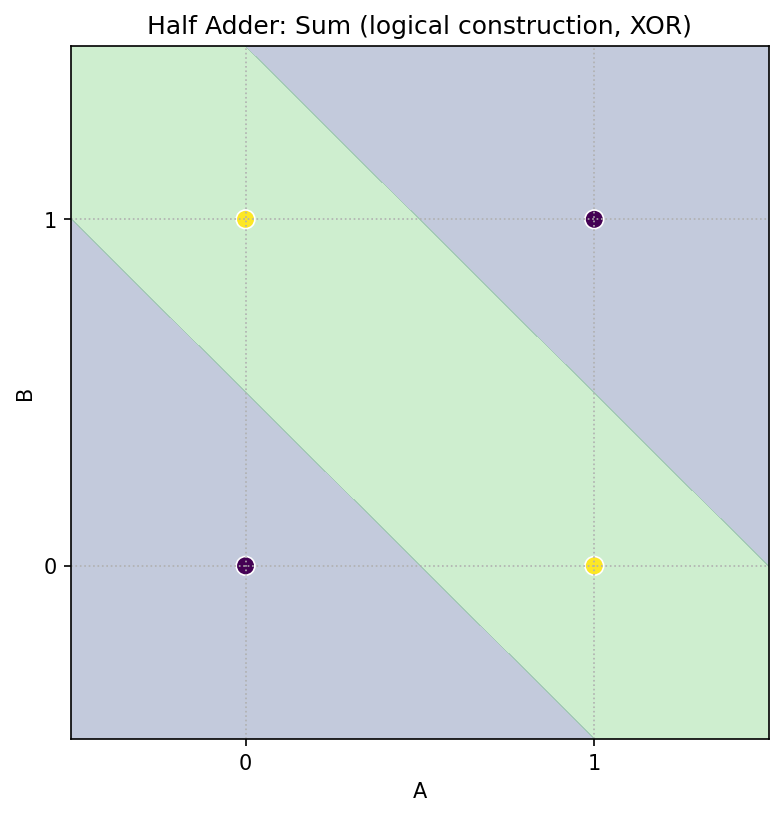
- Sum は XOR:片方だけ 1 のとき 1。
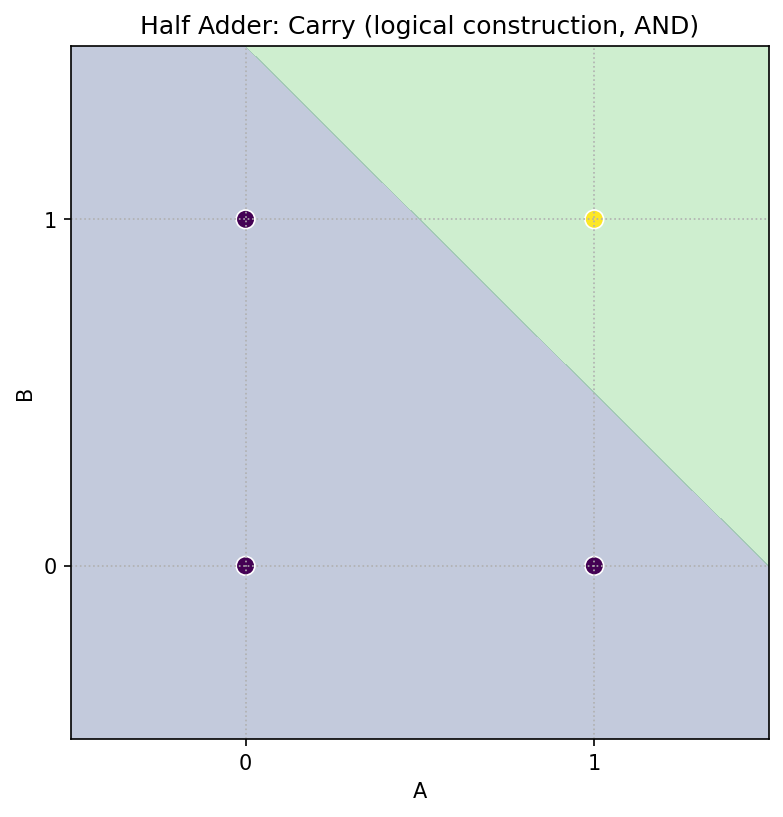
- Carry は AND:両方 1 のとき 1。
1.2 平面で観察(幾何)
(A,B) 平面で、
- Sum(XOR):赤(1)にしたい点は (0,1), (1,0)。1 本の直線では分けられません(線形分離不可)。
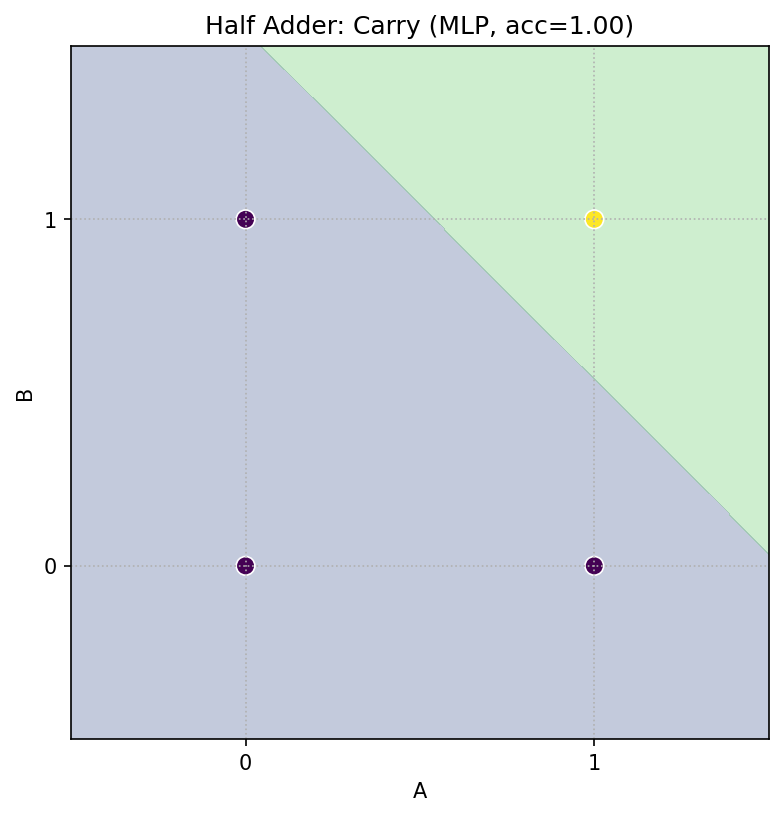
- Carry(AND):赤(1)は (1,1) のみ。直線 1 本で分けられます(線形分離可)。
1.3 論理ゲートで「構成的」に作る
- XOR は
XOR = (A OR B) AND NOT(A AND B)に分解可能。 -
隠れで
ORとNANDを作り、出力で AND を取れば Sum 完成。Carry は AND そのもの。
1.4 小さな MLP に学習させて確認
scikit-learn の MLPClassifier を使い、2 入力 → 2 出力(Sum, Carry)で学習します。
活性化は logistic(シグモイド)、少データなので solver='lbfgs' を使います。
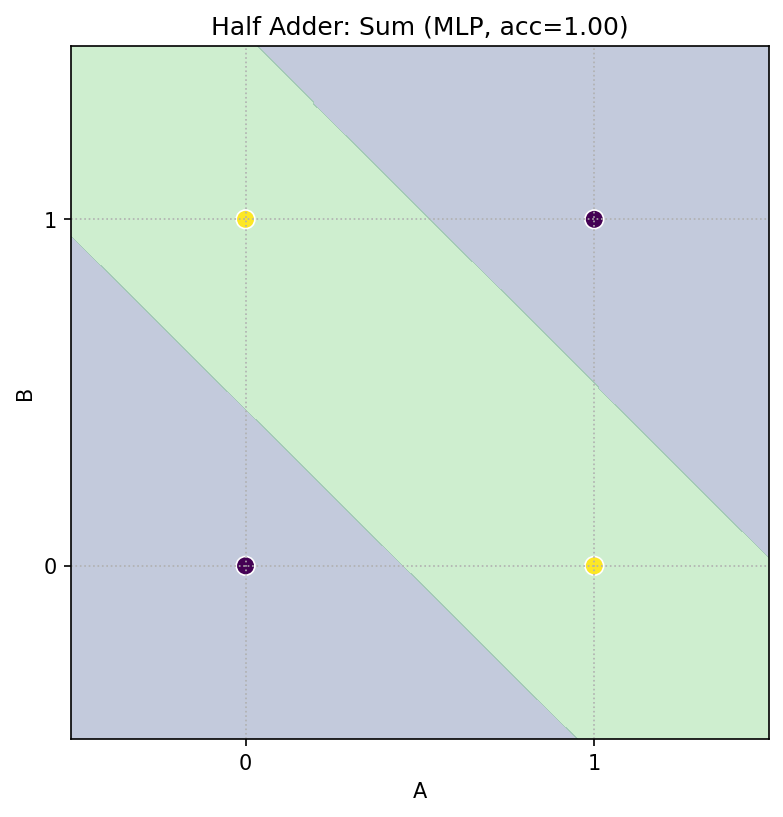
- 結果:Sum/Carry とも完全一致の決定領域が得られます。
ポイント
- 表現可能性:2 層があれば XOR を含む半加算器は作れる。
- 学習:小規模 MLP でもパラメータ探索で同じ機能に到達できる(ただし初期値や活性化で難易度は変わる)。
2. 全加算器:3 入力は 2D スライスで見る
2.1 真理表と式
入力 A, B, Cin に対し、出力は Sum と Cout(桁上がり):
-
Sum:
A ⊕ B ⊕ Cin(XOR を 2 回) -
Cout(多数決):
Cout = (A ∧ B) ∨ (A ∧ Cin) ∨ (B ∧ Cin)- あるいは
Cout = (A ∧ B) ∨ (Cin ∧ (A ⊕ B))
2.2 2D スライスで幾何を直感化
3 入力は 2D で見づらいので、Cin を固定して (A,B) 平面を 2 枚に分けます。
-
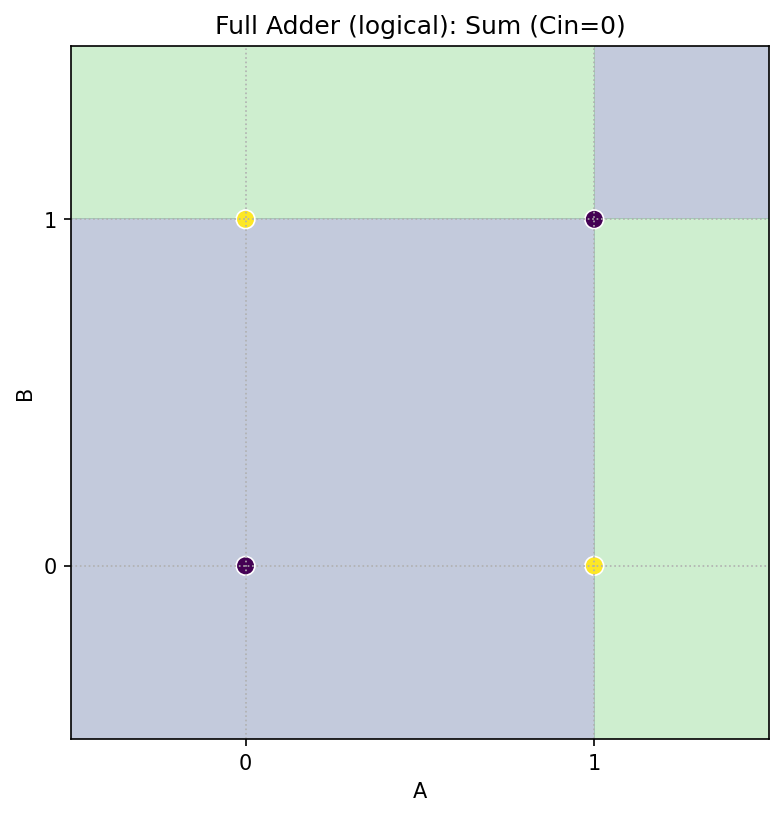
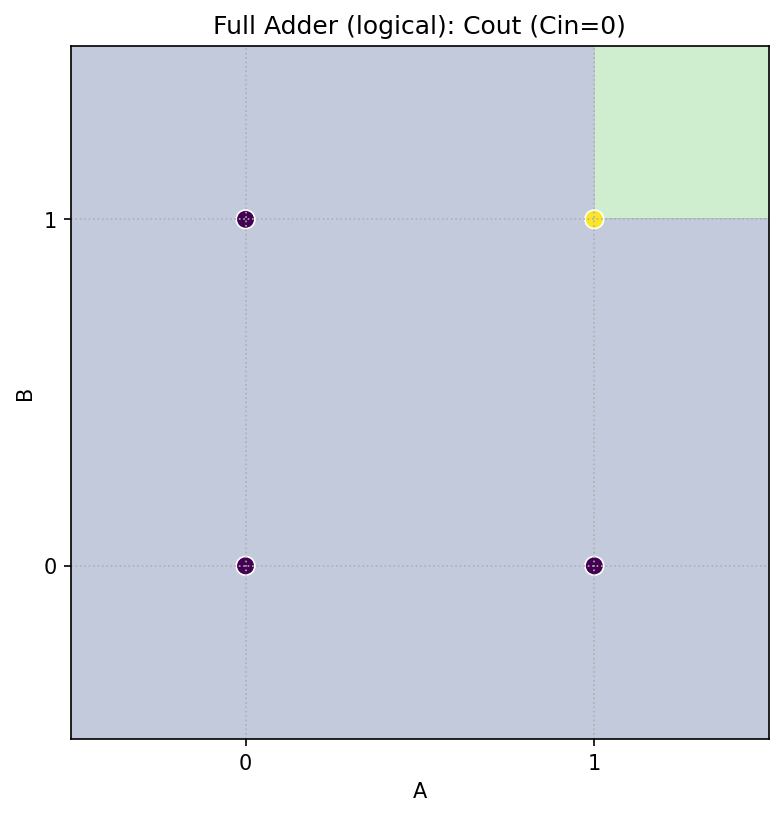
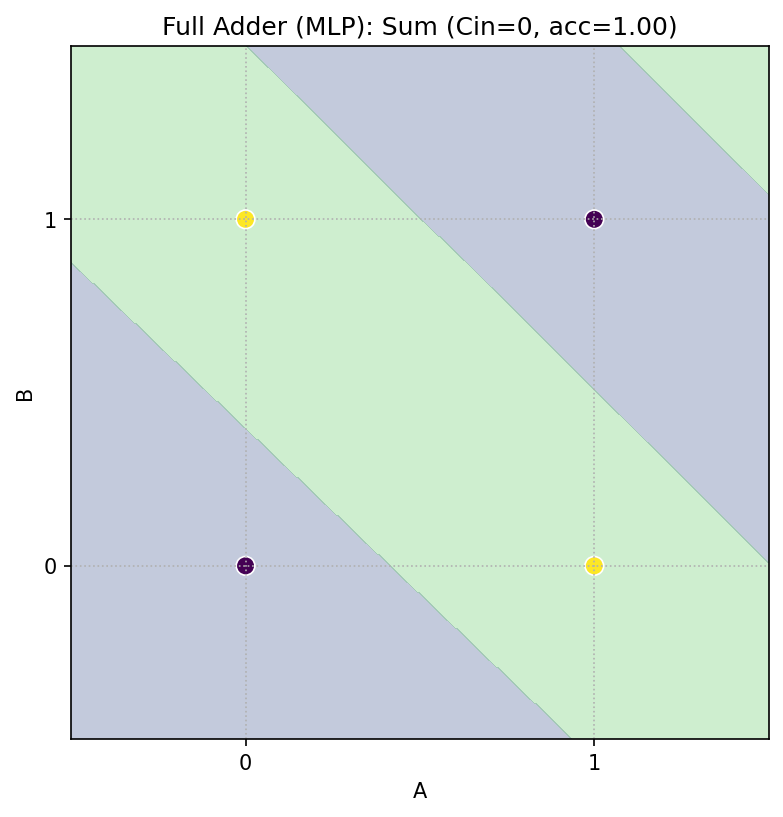
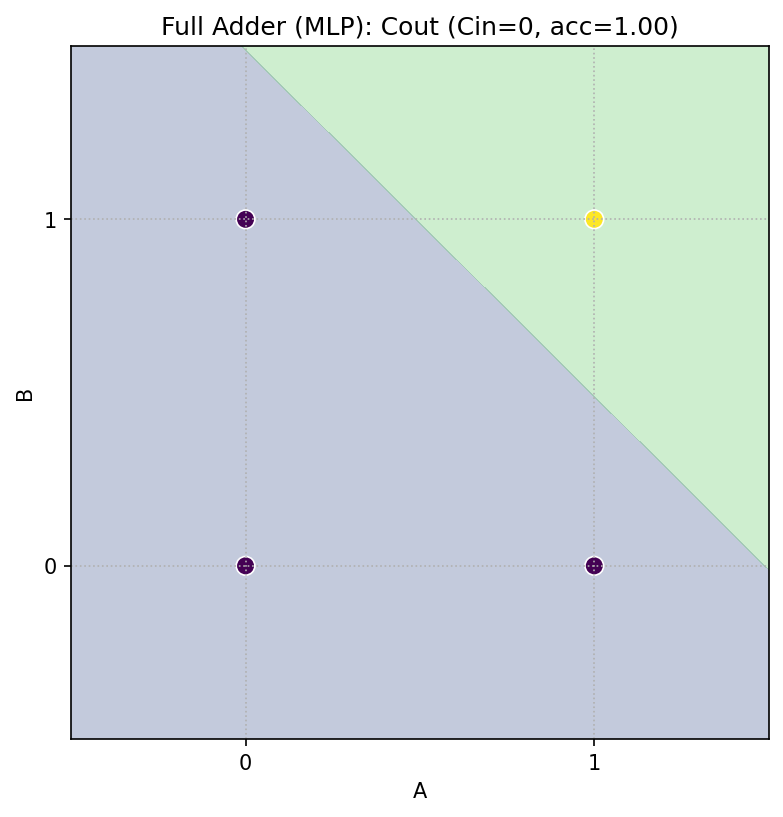
Cin=0 のとき
-
Sum = A ⊕ B(半加算器の Sum と同じ) -
Cout = A ∧ B(AND)
-
-
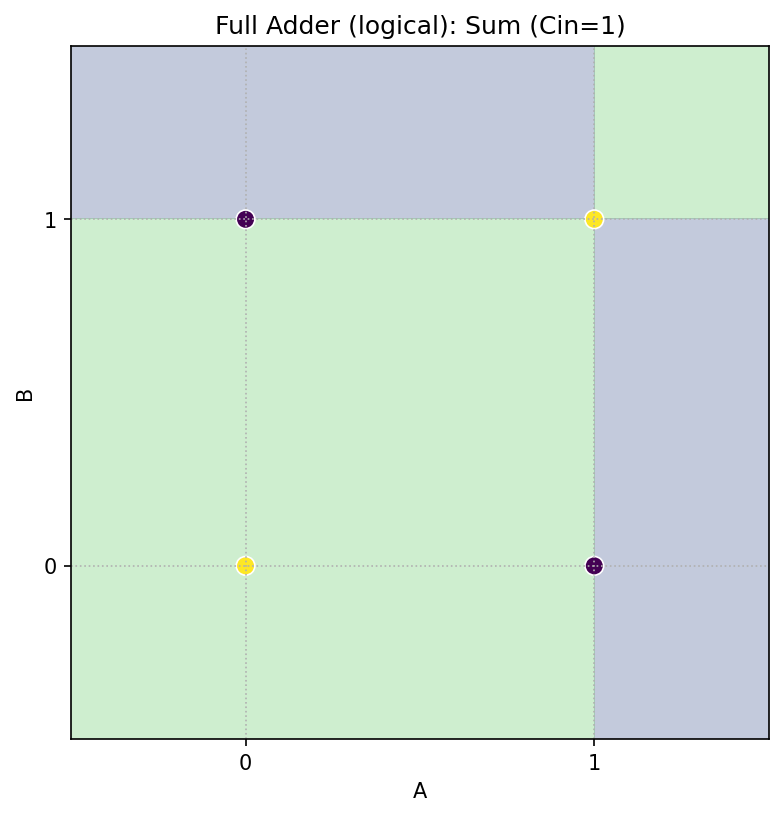
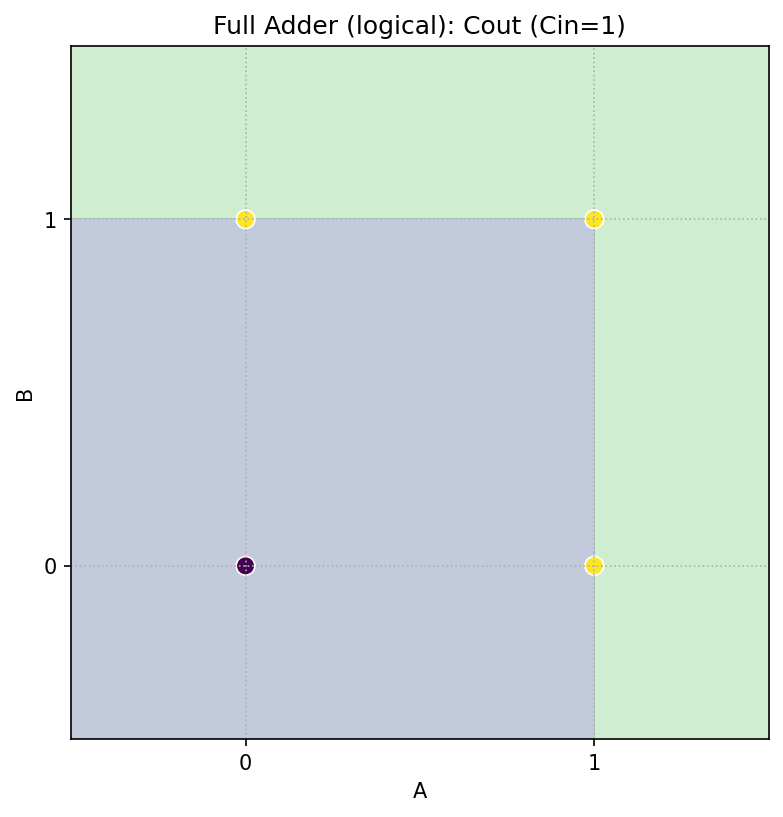
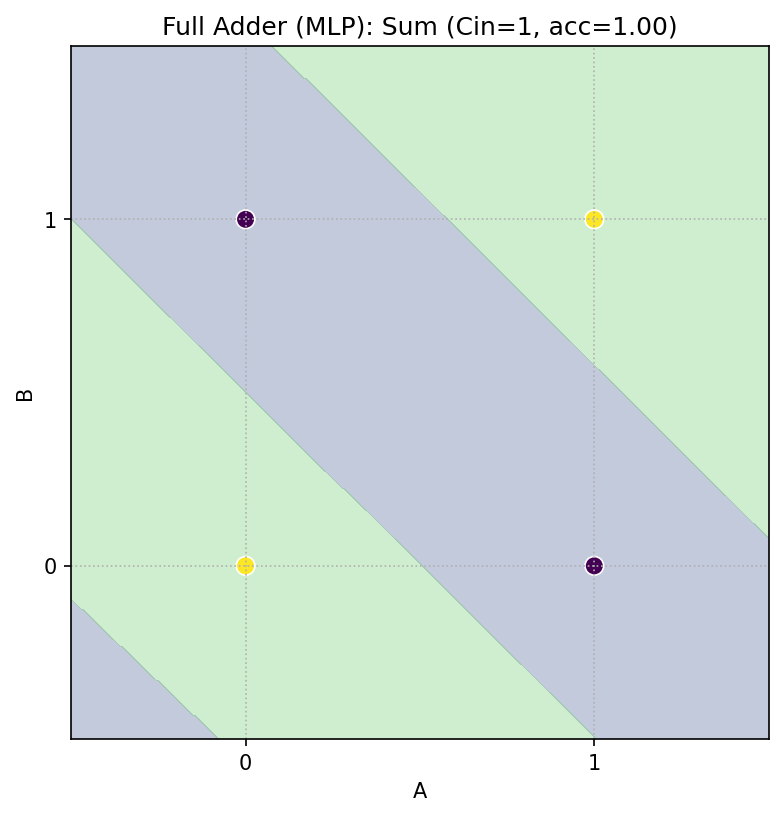
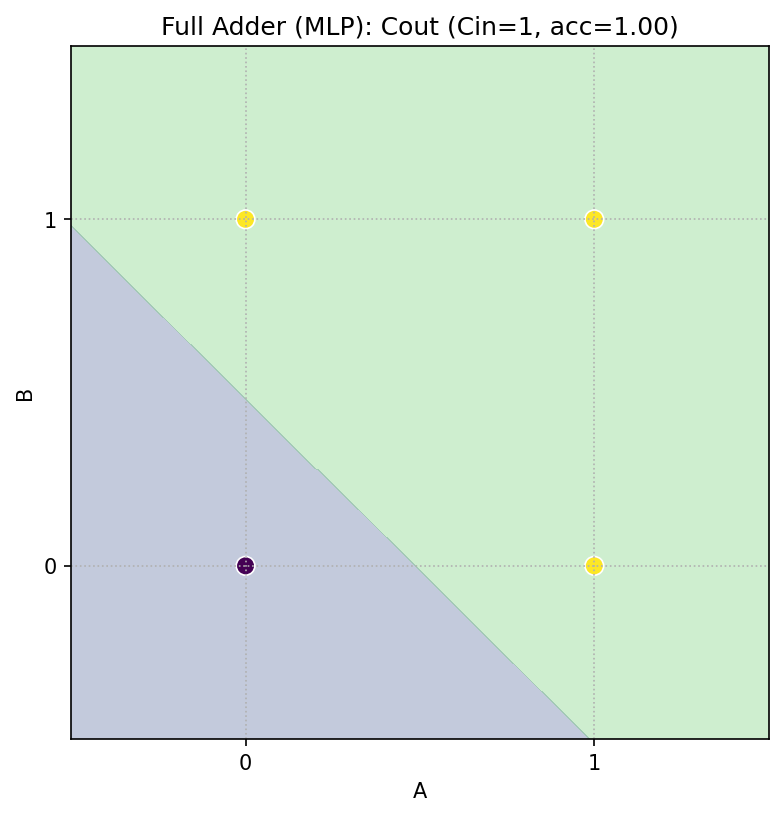
Cin=1 のとき
-
Sum = NOT(A ⊕ B)(XOR の反転) -
Cout = A ∨ B(OR)
-
2.3 小さな MLP で全加算器を学習
3 入力 → 2 出力(Sum, Cout)の MLP を最小限で学習させ、Cin=0/1 の 2D スライスで決定領域を可視化します。
- 結果:真理表どおりの正しい識別領域が得られます。
3. 学びの整理
- 線形分離 vs 非線形:加算器は Sum(XOR 部分)が非線形、Carry/Cout は状況により線形で分けられる。
- 2 層のちから:XOR のような非線形も、隠れ層を 1 枚挟むだけで表現可能。
-
学習と表現の区別:
- 表現可能性(存在証明):「このネットワークなら作れる」
-
学習(到達可能性):「実際に学習でその重みに辿り着けるか」
小規模問題ではlogistic+lbfgsが堅実。大規模では初期値・正則化・活性化・最適化が重要になる。
- 3 入力の可視化:2D スライスで見る設計は、複雑さを増やしても直感を保つ有効な方法。
4. まとめ
- 半加算器・全加算器という身近な論理回路を題材に、決定領域の可視化でニューラルネットの表現力を体感しました。
付録:記事内の図をすべて再現するコード(保存つき・1セル)
そのまま実行すると
fig/配下に PNG が保存されます。本文中の「ここに図を貼り付け」に対応するファイル名はコメントに併記しています。
# %pip -q install scikit-learn
import os, numpy as np, matplotlib.pyplot as plt
from itertools import product
from sklearn.neural_network import MLPClassifier
np.random.seed(0)
os.makedirs("fig", exist_ok=True)
# ---------- 共通ユーティリティ ----------
def step(z): return (z >= 0).astype(int)
def grid2d(xmin=-0.5, xmax=1.5, ymin=-0.5, ymax=1.5, n=400):
xx, yy = np.meshgrid(np.linspace(xmin, xmax, n), np.linspace(ymin, ymax, n))
X = np.stack([xx.ravel(), yy.ravel()], axis=1)
return xx, yy, X
def plot_region_2d(Z, xx, yy, X_points, y_points, title, savepath):
plt.figure(figsize=(6,6))
plt.contourf(xx, yy, Z, levels=[-0.5,0.5,1.5], alpha=0.30)
plt.scatter(X_points[:,0], X_points[:,1], c=y_points, s=80, edgecolors='white', linewidths=0.8)
plt.title(title); plt.xlabel("A"); plt.ylabel("B")
plt.xlim(-0.5,1.5); plt.ylim(-0.5,1.5); plt.xticks([0,1]); plt.yticks([0,1]); plt.grid(True, ls=":")
plt.savefig(savepath, dpi=150, bbox_inches='tight'); plt.show()
# 真理値の4点・8点
AB = np.array(list(product([0,1],[0,1]))) # (A,B)
ABC = np.array(list(product([0,1],[0,1],[0,1]))) # (A,B,Cin)
# ---------- 1) 半加算器:論理で構成 ----------
# Sum = XOR = (A OR B) AND NOT(A AND B)
# Carry = AND
def OR(a, b): return step(a + b - 0.5) # w=[1,1], b=-0.5
def AND(a, b): return step(a + b - 1.5) # w=[1,1], b=-1.5
def NAND(a, b): return step(-a - b + 1.5) # AND の否定
# 可視化用グリッド
xx, yy, Xgrid = grid2d()
# 半加算器(論理合成)
H1_or = OR(Xgrid[:,0], Xgrid[:,1])
H2_nand = NAND(Xgrid[:,0], Xgrid[:,1])
SUM_logical = AND(H1_or, H2_nand) # XOR の構成
CARRY_logical = AND(Xgrid[:,0], Xgrid[:,1]) # AND
# ラベル点
y_sum_pts = ((AB[:,0] ^ AB[:,1])).astype(int)
y_carry_pts = ((AB[:,0] & AB[:,1])).astype(int)
plot_region_2d(SUM_logical.reshape(xx.shape), xx, yy, AB, y_sum_pts,
"Half Adder: Sum (logical construction, XOR)", "fig/ha_sum_manual.png")
plot_region_2d(CARRY_logical.reshape(xx.shape), xx, yy, AB, y_carry_pts,
"Half Adder: Carry (logical construction, AND)", "fig/ha_carry_manual.png")
# ---------- 2) 半加算器:MLPで学習 ----------
# 入力 X2=(A,B), 出力 Y2=[Sum, Carry]
X2 = AB.copy()
Y2 = np.c_[y_sum_pts, y_carry_pts] # shape (4,2)
mlp_ha = MLPClassifier(hidden_layer_sizes=(3,), activation='logistic',
solver='lbfgs', alpha=1e-4, random_state=0, max_iter=10000)
mlp_ha.fit(X2, Y2)
# グリッドで予測(各出力を別図として可視化)
Y2_grid = mlp_ha.predict(Xgrid) # shape (n_grid, 2)
Z_sum_mlp = Y2_grid[:,0].reshape(xx.shape)
Z_carry_mlp = Y2_grid[:,1].reshape(xx.shape)
plot_region_2d(Z_sum_mlp, xx, yy, AB, y_sum_pts,
f"Half Adder: Sum (MLP, acc={mlp_ha.score(X2,Y2):.2f})", "fig/ha_sum_mlp.png")
plot_region_2d(Z_carry_mlp, xx, yy, AB, y_carry_pts,
f"Half Adder: Carry (MLP, acc={mlp_ha.score(X2,Y2):.2f})", "fig/ha_carry_mlp.png")
# ---------- 3) 全加算器:論理で構成 ----------
# Sum = A ^ B ^ Cin
# Cout = (A&B) | (A&Cin) | (B&Cin)
def XOR(a, b): return (a ^ b).astype(int)
def full_adder_sum(a, b, c):
return XOR(XOR(a.astype(int), b.astype(int)), c.astype(int))
def full_adder_cout(a, b, c):
return ((a & b) | (a & c) | (b & c)).astype(int)
# Cin 固定の 2D スライスを作って可視化
def plot_fa_logical_slice(cin_value, title_prefix):
xx, yy, X = grid2d()
A, B = X[:,0].astype(int), X[:,1].astype(int)
C = np.full_like(A, cin_value)
Z_sum = full_adder_sum(A,B,C).reshape(xx.shape)
Z_cout = full_adder_cout(A,B,C).reshape(xx.shape)
# ラベル点(A,B のみ表示)
AB_pts = AB
y_sum_pts = full_adder_sum(AB_pts[:,0], AB_pts[:,1], np.full(4, cin_value))
y_cout_pts = full_adder_cout(AB_pts[:,0], AB_pts[:,1], np.full(4, cin_value))
plot_region_2d(Z_sum, xx, yy, AB_pts, y_sum_pts,
f"{title_prefix}: Sum (Cin={cin_value})", f"fig/fa_manual_sum_c{cin_value}.png")
plot_region_2d(Z_cout, xx, yy, AB_pts, y_cout_pts,
f"{title_prefix}: Cout (Cin={cin_value})", f"fig/fa_manual_cout_c{cin_value}.png")
plot_fa_logical_slice(0, "Full Adder (logical)")
plot_fa_logical_slice(1, "Full Adder (logical)")
# ---------- 4) 全加算器:MLPで学習 ----------
# 入力 X3=(A,B,Cin), 出力 Y3=[Sum, Cout]
X3 = ABC.copy()
Y3 = np.c_[ full_adder_sum(ABC[:,0], ABC[:,1], ABC[:,2]),
full_adder_cout(ABC[:,0], ABC[:,1], ABC[:,2]) ]
mlp_fa = MLPClassifier(hidden_layer_sizes=(4,), activation='logistic',
solver='lbfgs', alpha=1e-4, random_state=0, max_iter=10000)
mlp_fa.fit(X3, Y3)
def plot_fa_mlp_slice(cin_value, title_prefix):
xx, yy, X = grid2d()
A, B = X[:,0], X[:,1]
C = np.full_like(A, cin_value)
X_grid3 = np.c_[A, B, C]
Y_pred = mlp_fa.predict(X_grid3) # (n,2)
Z_sum = Y_pred[:,0].reshape(xx.shape)
Z_cout = Y_pred[:,1].reshape(xx.shape)
# ラベル点(A,B のみ表示)
AB_pts = AB
y_sum_pts = full_adder_sum(AB_pts[:,0], AB_pts[:,1], np.full(4, cin_value))
y_cout_pts = full_adder_cout(AB_pts[:,0], AB_pts[:,1], np.full(4, cin_value))
plot_region_2d(Z_sum, xx, yy, AB_pts, y_sum_pts,
f"{title_prefix}: Sum (Cin={cin_value}, acc={mlp_fa.score(X3,Y3):.2f})",
f"fig/fa_mlp_sum_c{cin_value}.png")
plot_region_2d(Z_cout, xx, yy, AB_pts, y_cout_pts,
f"{title_prefix}: Cout (Cin={cin_value}, acc={mlp_fa.score(X3,Y3):.2f})",
f"fig/fa_mlp_cout_c{cin_value}.png")
plot_fa_mlp_slice(0, "Full Adder (MLP)")
plot_fa_mlp_slice(1, "Full Adder (MLP)")
print("Saved figures under ./fig :",
[f for f in sorted(os.listdir("fig")) if f.endswith(".png")])