Advent Calendar 12日目の記事 組合せ最適化で推理パズルを解く
Advent Calendar 14日目の記事 組合せ最適化でウォールロジックを解く
これなに
ペイントエリアを、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。
自分でも試してみたい人は、下記を参考にしてください。
問題
- 盤面上にある、太線で区切られた部分(タイル)のいくつかを黒くぬります。
- 盤面の数字は、その数字の入っているマスにタテヨコに隣り合うマスのうち、黒マスになるマスの数を表します。
- 数字のマスが黒マスになることもあります。
- どのタイルも、すべてのマスをぬるかすべてのマスをぬらずにおくかのどちらとし、タイルの一部のマスだけをぬってはいけません。
- すべての黒マスはつながること。
- 黒白マスとも、2×2以上はだめ。
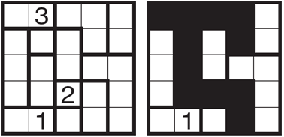
下記は、左が問題で、右が答えです。
dataにタイルのグループが、numsにヒントの「行、列、個数」が入っているとします。
python
import pandas as pd, matplotlib.pyplot as plt
from pulp import LpProblem, lpSum, value
from ortoolpy import addbinvars, unionfind
data = """\
AABBC
DEFBC
DGFHH
DGIJH
KKLJH""".splitlines()
nums = [[0,1,3], [3,2,2], [4,1,1]]
変数表
下記のような変数表を作成します。各行の変数は0または1をとります。
変数の値が1ならば、該当行 該当列のマスが黒になります。
「字」はdataの値です。
| 行 | 列 | 字 | Var | |
|---|---|---|---|---|
| 0 | 0 | 0 | A | v000001 |
| 1 | 0 | 1 | A | v000002 |
| ... | ... | ... | ... | ... |
python
ni, nj = len(data), len(data[0])
a = pd.DataFrame([(i,j,data[i][j]) for i in range(ni)
for j in range(nj)], columns=list('行列字'))
a['Var'] = addbinvars(len(a))
a[:2]
数理モデルを作り解く
変数表ができたので、ペイントエリアの解になるように、制約条件を追加し数理モデルを作成し、解きましょう。
- 2×2の白および2×2の黒がないこと。
-
queryで2x2を取り出して、黒の数を1,2,3とします。
-
- タイル内は同じこと。
- タイル内の隣り合う変数を等しくします。
- 数字は周りの黒の数と等しいこと。
- 上下左右は、差分の絶対値の和が1のものです。
- 全ての黒がつながること。
- 繋がっていなかったら、その解の全白のマスに少なくとも1つ黒を置いて解きなおします。
python
m = LpProblem()
for i in range(ni-1):
for j in range(nj-1):
e = lpSum(a.query(f'{i}<=行<={i+1}&{j}<=列<={j+1}').Var)
m += e >= 1 # 2×2の白がない
m += e <= 3 # 2×2の黒がない
for _,v in a.groupby('字'):
for vi, vj in zip(v.Var, v.Var[1:]):
m += vi == vj # タイル内は同じ
for i, j, k in nums: # 数字は周りの黒の数と等しい
m += lpSum(a.query(f'abs(行-{i})+abs(列-{j})==1').Var) == k
while True:
m.solve()
r = a.Var.apply(value)
if unionfind.isconnected(r.values.reshape(ni,nj)):
break # 全ての黒がつながる
m += lpSum(a[r==0].Var) >= 1
結果の表示
python
plt.imshow((1-r).values.reshape(ni,nj), cmap='gray', interpolation='none')
plt.show()
解けていることが確認できます。
以上