Advent Calendar 13日目の記事 組合せ最適化でペイントエリアを解く
Advent Calendar 15日目の記事 組合せ最適化でののぐらむを解く
これなに
ウォールロジックを、Pythonで組合せ最適化モデルを作って解きます。
解く楽しみは、モデル化を工夫することになります。
自分でも試してみたい人は、下記を参考にしてください。
問題
- 数字が記入されているマスからその数字の数だけ縦と横に線を引きます
- 1つのマスには1本の線しか引くことができません
- 数字が記入されているマスには線を引くことができません
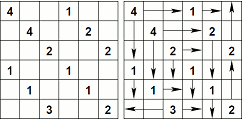
下記は、左が問題で、右が答えです。
dataにヒントの数が入っているとします。
python
import pandas as pd
from itertools import product
from pulp import LpProblem, lpSum, lpDot, value
from ortoolpy import addvars, addbinvars
data = """\
4..1..
.4..2.
..2..2
1..1..
.1..1.
..3..2""".split()
変数表
下記のような変数表を作成します。各行の変数は0または1をとります。
変数の値が1ならば、該当行 該当列のマスが黒になります。
「向」は{0:左, 1:上, 2:右, 3:下}です。VDirはその方向かどうか、VLenは矢印の長さです。
| 行 | 列 | 向 | VDir | VLen | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | v000001 | v000145 |
| 1 | 0 | 0 | 1 | v000002 | v000146 |
| ... | ... | ... | ... | ... | ... |
python
ni, nj = len(data), len(data[0])
mx = max(ni, nj)
a = pd.DataFrame([(i,j,k) for i,j,k in product(range(ni),
range(nj),range(4))], columns=list('行列向'))
a['VDir'] = addbinvars(len(a))
a['VLen'] = addvars(len(a))
a[:2]
数理モデルを作り解く
変数表ができたので、ウォールロジックの解になるように、制約条件を追加し数理モデルを作成し、解きましょう。
- 数字があれば、方向別長さの和に等しく、かつその位置に矢印がないこと (1)
- 数字がなければ矢印は1方向のみ (2)
- 数字がなければ矢印の方向に長さを1足すこと (3)
python
drc = [(-1, 0, 0), (0, -1, 1), (0, 1, 2), (1, 0, 3)]
m = LpProblem()
for i,j in product(range(ni), range(nj)):
b = a[(a.行==i)&(a.列==j)]
if data[i][j].isdigit():
m += lpSum(a[(a.行==i+y)&(a.列==j+x)&(a.向==k)].VLen
for y,x,k in drc) == int(data[i][j]) # (1)
m += lpSum(b.VLen) == 0 # (1)
continue
m += lpSum(b.VDir) == 1 # (2)
for y,x,k in drc:
r = b[b.向==k].iloc[0]
m += r.VLen <= mx * r.VDir # (3)
m += r.VLen <= r.VDir + lpSum(
a[(a.行==i+y)&(a.列==j+x)&(a.向==k)].VLen) # (3)
m.solve()
結果の表示
python
a['Val'] = a.VDir.apply(value)
print('\n'.join(''.join(' '+(data[i][j] if data[i][j].isdigit()
else '↑←→↓'[int(value(lpDot([0,1,2,3],a[(a.行==i)&(a.列==j)].Val)))])
for j in range(ni)) for i in range(nj)))
>>>
4 → → 1 → ↑
↓ 4 → → 2 ↑
↓ ↓ 2 → ↓ 2
1 ↓ ↓ 1 ↓ ↑
↓ 1 → ↓ 1 ↑
← ← 3 → ↓ 2
解けていることが確認できます。
以上