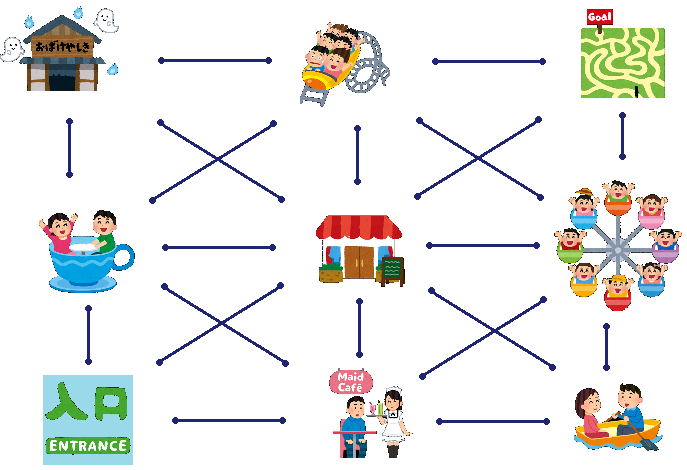
これなに

「python Adventvent Calendar 2017 16日目」TDLアトラクションの組み合わせ最適化をしてみるでは考慮されてない移動時間を入れて、組合せ最適化で解いてみます。

以前にも同じ記事を書いているのを忘れてました。今回は、オクトーバー・スカイ社のメルマガに出ていた多面体論の持ち上げ操作¹で強化した制約を入れています。

問題

8つのアトラクションがある遊園地でデートをします。200分の制限時間の中で総満足度を最大化しましょう。
（巡回セールスマン問題と違い、全て回らなくてもOKです）

Pythonで解く

アトラクション表を作ります。

python3

import pandas as pd

# パラメータ
atra = '入口 喫茶 ボート カップ レストラン 観覧車 お化け屋敷 コースター 迷路'.split()
prio = [0,50,36,45,79,55,63,71,42] # 満足度
tims = [0,20,28,15,35,17,18,14,22] # 滞在時間
timm = [[0,1,9],[0,3,7],[0,4,12],[1,2,11],[1,3,12],[1,4,7],[1,5,13],[2,4,14],[2,5,8],[3,4,11],
        [3,6,7],[3,7,12],[4,5,9],[4,6,13],[4,7,9],[4,8,13],[5,7,13],[5,8,7],[6,7,7],[7,8,6]]
n = len(atra)

# アトラクション表
dfa = pd.DataFrame(list(zip(atra,prio,tims)),columns=['Atra','Prio','TimU'])
dfa[:3]

	Atra	Prio	TimU
0	入口	0	0
1	喫茶	50	20
2	ボート	36	28
...	...	...	...

移動時間表を作ります。

python3

# 移動時間表
dft = pd.DataFrame([c for i,j,t in timm for c in [(i,j,t),(j,i,t)]],
    columns=['I','J','TimM'])
dft[:4]

	I	J	TimM
0	0	1	9
2	0	3	7
4	0	4	12
1	1	0	9
...	...	...	...

解きます。

python3

def solve_route(dfa, dft, limit_time, lower=0):
    """
    入口(index=0)から複数のアトラクションから時間内に満足度最大のものを選ぶ
    入力
        dfa: アトラクション表(Atra:アトラクション, Prio:満足度, TimU:滞在時間)
        dft: 移動時間表(I:点i, J:点j, TimM:移動時間)
        limit_time: 制限時間
        lower: 最低アトラクション数
    出力
        満足度の和、時間、利用順序
    """
    from more_itertools import iterate, take
    from pulp import LpProblem, LpMaximize, lpDot, lpSum, value
    from ortoolpy import addvars, addbinvars
    dfa,dft = dfa.copy(),dft.sort_values(['I', 'J'])
    m = LpProblem(sense=LpMaximize)
    dfa['VarS'] = [1] + addvars(n-1) # アトラクションを選ぶか
    dft['VarIJ'] = addbinvars(len(dft)) # IからJに行くか
    dft['VarJI'] = dft.sort_values(['J', 'I']).VarIJ.values # JからIに行くか
    u = [0]+addvars(n-1) # 入口から何番目か
    m += lpDot(dfa.Prio, dfa.VarS) # 目的関数
    e = lpDot(dfa.TimU, dfa.VarS) + lpDot(dft.TimM, dft.VarIJ)
    m += e <= limit_time # 制限時間
    for _,r in dfa.iterrows():
        m += r.VarS == lpSum(dft[dft.J==r.name].VarIJ) # 選んだら来る
    for _,v in dft.groupby('I'):
        m += lpSum(v.VarIJ) == lpSum(v.VarJI) #入ったら出る
    for _,(i,j,_,vij,vji) in dft.query('I!=0 & J!=0').iterrows():
        m += u[i]+1 -(n-1)*(1-vij) + (n-3)*vji <= u[j] #持ち上げポテンシャル制約(MTZ)
    for _,(_,j,_,v0j,vj0) in dft.query('I==0').iterrows():
        m += 1+(1-v0j) +(lower-3)*vj0 <= u[j]  #持ち上げ下界制約
    for _,(i,_,_,vi0,v0i) in dft.query('J==0').iterrows():
        m += u[i] <= (n-1)-(1-vi0)-(n-3)*v0i #持ち上げ上界制約
    m.solve()
    if m.status != 1:
        return -1, -1, []
    dft['ValIJ'] = dft.VarIJ.apply(value)
    dc = dict(dft[dft.ValIJ>0.5].values[:,:2])
    return value(m.objective), value(e), [dfa.Atra[i] 
        for i in take(int(value(lpSum(dfa.VarS)))+1, iterate(lambda k: dc[k], 0))]
solve_route(dfa, dft, 200)
>>>
(405.0,
 200.0,
 ['入口', 'カップ', 'お化け屋敷', 'コースター',
  '迷路', '観覧車', 'レストラン', '喫茶', '入口'])

滞在時間と移動時間の和が200で、総満足度が405になりました。

以上

今回の問題は、メルマガの巡回セールスマンと違うので、効果のほどは不明です。 ↩

組合せ最適化でデートコースを決めよう（強い定式化版）

これなに

問題

Pythonで解く