やったこと
- 手書き数字の画像データをSVMで分類
- Cross Validation でモデルの score を評価
- ハイパーパラメータ C を変えて、score がどう変わる確かめる
- ハイパーパラメータ gamma を変えて、score がどう変わる確かめる
ソースはこちら。
ライブラリとデータのインポート
交差検定用ライブラリ"cross_validation"をインポート。データは手書き数字のdigitsを使用。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import svm, datasets, cross_validation
digits = datasets.load_digits()
X_digits = digits.data
y_digits = digits.target
交差検定の方法とパラメータ設定
交差検定の方法は以下のようなものが用意されている。
- kFold(n, k): n個の標本データをk個のバッチ(塊)に分割。1バッチをテスト用に、残りの(k-1)バッチをトレーニング用に使う。テスト用に使うデータセットを変えて、k回検定を繰り返す。
- StratifiedKFold (y, k):分割後のデータセット内のラベルの比率を保ったまま、データをk個に分割。
- LeaveOneOut (n):kFoldで k = n のケースと等価。データの標本数が少ない時に。
- LeaveOneLabelOut (labels):与えられたラベルに従ってデータを分割。例えば年次に関するデータを扱う場合、年ごとのデータに分けて検定を行う場合など。
今回は、最もシンプルなKFoldを使う。分割数は4とした。後で気がついたけど、KFoldのところで、変数'shuffle=true'と定義すれば、自動でデータ順序をランダムに並び替えてくれるみたい。
np.random.seed(0) # 乱数のシード設定、0じゃなくてもなんでもいい
indices = np.random.permutation(len(X_digits))
X_digits = X_digits[indices] # データの順序をランダムに並び替え
y_digits = y_digits[indices]
n_fold = 4 # 交差検定の回数
k_fold = cross_validation.KFold(n=len(X_digits),n_folds = n_fold)
# k_fold = cross_validation.KFold(n=len(X_digits),n_folds = n_fold, shuffle=true)
# とすれば、最初の4行は不要。
SVM の変数Cを変えて実験
ハイパーパラメータCを変えて、モデルの評価値がどのように変化するか確かめる。Cは誤判定をどの程度許容するかを決めるパラメータ。SVMのカーネルはガウシアンカーネルとした。
参考:過去記事「SVMで手書き数字の認識」
C_list = np.logspace(-8, 2, 11) # C
score = np.zeros((len(C_list),3))
tmp_train, tmp_test = list(), list()
# score_train, score_test = list(), list()
i = 0
for C in C_list:
svc = svm.SVC(C=C, kernel='rbf', gamma=0.001)
for train, test in k_fold:
svc.fit(X_digits[train], y_digits[train])
tmp_train.append(svc.score(X_digits[train],y_digits[train]))
tmp_test.append(svc.score(X_digits[test],y_digits[test]))
score[i,0] = C
score[i,1] = sum(tmp_train) / len(tmp_train)
score[i,2] = sum(tmp_test) / len(tmp_test)
del tmp_train[:]
del tmp_test[:]
i = i + 1
検定の評価値を見るだけならもっと簡単に書ける。変数n_jobsで使用するCPU数も指定可能。-1は全CPUを使用。
cross_validation.cross_val_score(svc, X_digits, y_digits, cv=k_fold, n_jobs=-1)
arrayで評価値を出力してくれる。
array([ 0.98888889, 0.99109131, 0.99331849, 0.9844098 ])
結果をグラフで可視化
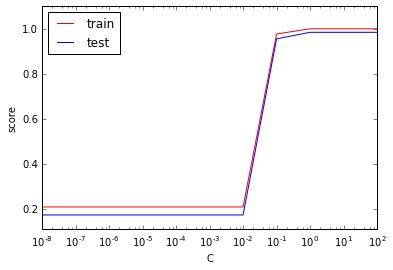
Cを横軸にして、トレーニング時の評価値、テスト時の評価値をプロット。Cが小さいと誤判定を許容しすぎるためか、精度が上がらない。
xmin, xmax = score[:,0].min(), score[:,0].max()
ymin, ymax = score[:,1:2].min()-0.1, score[:,1:2].max()+0.1
plt.semilogx(score[:,0], score[:,1], c = "r", label = "train")
plt.semilogx(score[:,0], score[:,2], c = "b", label = "test")
plt.axis([xmin,xmax,ymin,ymax])
plt.legend(loc='upper left')
plt.xlabel('C')
plt.ylabel('score')
plt.show
SVM の変数gammaを変えて実験
続いて、Cを100に固定して、gammaを変えて同様の実験。ガンマが大きいほど、分類境界が複雑になる。
g_list = np.logspace(-8, 2, 11) # C
score = np.zeros((len(g_list),3))
tmp_train, tmp_test = list(), list()
i = 0
for gamma in g_list:
svc = svm.SVC(C=100, gamma=gamma, kernel='rbf')
for train, test in k_fold:
svc.fit(X_digits[train], y_digits[train])
tmp_train.append(svc.score(X_digits[train],y_digits[train]))
tmp_test.append(svc.score(X_digits[test],y_digits[test]))
score[i,0] = gamma
score[i,1] = sum(tmp_train) / len(tmp_train)
score[i,2] = sum(tmp_test) / len(tmp_test)
del tmp_train[:]
del tmp_test[:]
i = i + 1
結果がこちら。
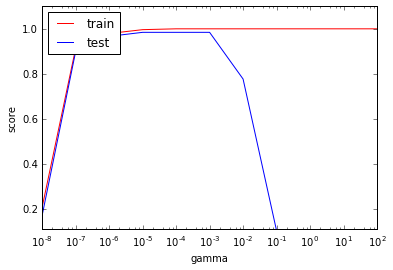
ガンマを大きくしていくと、トレーニング時の精度も、テスト時の精度もどちらも高くなるが、0.001を過ぎたあたりから、トレーニング時の精度は変わらないが、テスト時の精度が下がっていく。複雑性許容しすぎて、過学習が起こっていると思われる。変数の設定が重要なことがわかる。