前にビックデータについてのセミナーに行ったときに次元の呪いという言葉を聞いたので調べることに。
要約するとデータの次元数が増えることで、データの距離が離れる現象。
1次元のデータは平均値に最もデータが集中するのに、複数次元になると平均値にはデータがなくなってしまうんです。
機械学習をやっていくと突き当ったりするらしい。
カーネル法はこれを利用することで、分類の難しいデータ間のマージンを作り出しているとか・・・
とりあえず次元の呪いをRで確認する。
まず1次元でプロット
cur_of_dim <-data.frame(matrix(rnorm(1000,0,1),nrow=100,ncol=1))
mean(dist(cur_of_dim))
[1] 1.110581
hist(dist(cur_of_dim))
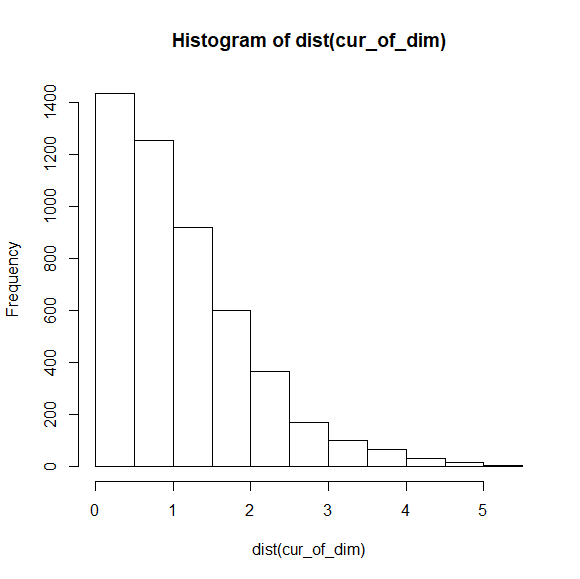
とりあえず一次元のデータを発生させた。
平均0, 標準偏差1のデータの平均からの距離をヒストグラムにした。
平均からの距離の平均は1.11だった。
距離は絶対値的なものなので、正規分布を半分に折りたたんだような図になった。
2次元にしてみる。
cur_of_dim <-data.frame(matrix(rnorm(1000,0,1),nrow=100,ncol=2))
mean(dist(cur_of_dim))
[1] 1.801263
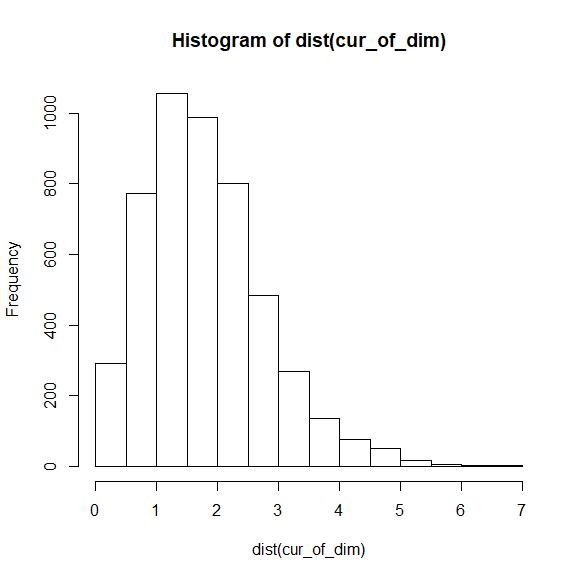
hist(dist(cur_of_dim))
2次元にしただけでも平均の0の数が減っていた。
なんで同じ平均のデータが減るんでしょう?
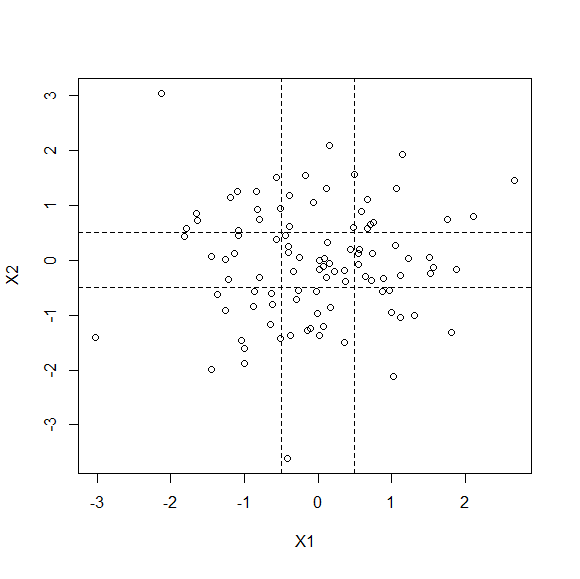
2次元をプロットしてみます。
平均に近い部分として、0±0.5ほどを点線にしてみます。
ついでにこの点線の中に何個のデータがあるのか確認してみます。
plot(cur_of_dim)
abline(h=c(0.5,-0.5),lty=2)
abline(v=c(0.5,-0.5),lty=2)
kakunin <-cur_of_dim[cur_of_dim[,1] >= -0.5 & cur_of_dim[,2] >= -0.5 & 0.5 > cur_of_dim[,1] & 0.5 > cur_of_dim[,2],]
nrow(kakunin)
[1] 16
100個のデータ中で0の周辺にあるデータは16個と少なくなっていました。
(ちなみに一次元では38個ありました。)
これを繰り返していくから平均にぴったり乗るデータは少なくなるんですね。
このまま次元を増やしていきます。
# 5次元
cur_of_dim <-data.frame(matrix(rnorm(1000,0,1),nrow=100,ncol=5))
mean(dist(cur_of_dim))
[1] 2.92333
# 10次元
cur_of_dim <-data.frame(matrix(rnorm(1000,0,1),nrow=100,ncol=10))
mean(dist(cur_of_dim))
[1] 4.394134
# 50次元
cur_of_dim <-data.frame(matrix(rnorm(1000,0,1),nrow=100,ncol=50))
mean(dist(cur_of_dim))
[1] 10.15969
# 100次元
cur_of_dim <-data.frame(matrix(rnorm(1000,0,1),nrow=100,ncol=100))
mean(dist(cur_of_dim))
[1] 14.55681
どんどん離れていくのが確認できました。
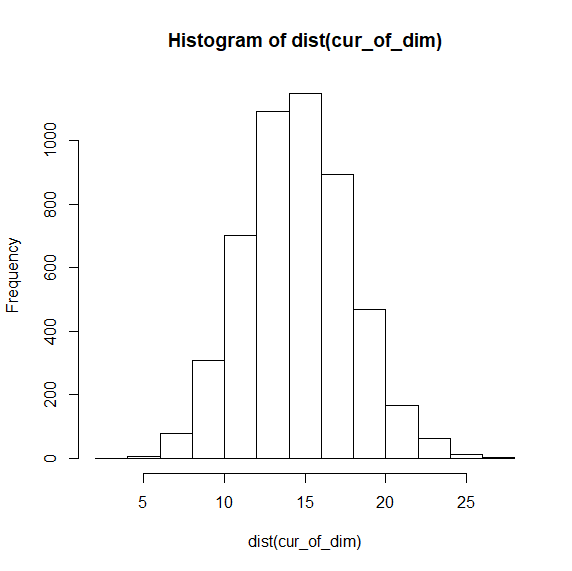
hist(dist(cur_of_dim))
ヒストグラム見てみるとほとんど平均の0にありませんでした。
これが次元の呪いなのでしょう。
正規分布でやりましたが、分布が変われば結果も変わりそう。
それはまた今度に。
普通の人でいいから恋人が欲しいという人がいますが、
平均的を求めるのは逆に難しそうです。
きっと普通の恋人ができないのは次元の呪いのせいなんです!
それは話が違う?
以上です
(一次元でもピッタリ平均値なんて存在せんやろ!って言われたことがありましたが、それはイプシロン-デルタ論法の話だったようなので、もしそちらを探している人がいたらそれとは別の話です。)