正規分布について
この記事はタニング=クルーガー効果によってイキってしまった私が書いていく正規分布についての記事です。
正規分布の歴史
正規分布とはドモアブルやラプラスによって1700年~1800年ごろに基礎が作られ、
ガウスが中心極限定理を発表したことで大きな発展につながったもの。
分布はベルの形をしており、データの中心・平均値が山の頂点となる。
平均値から離れた箇所にも稀ながら確率が存在することを表している。
ベル型を成す関数であり、マイナス無限から無限までを積分すると1になるような数式として考え生み出された。
Rがあれば数式理解も無理じゃない!
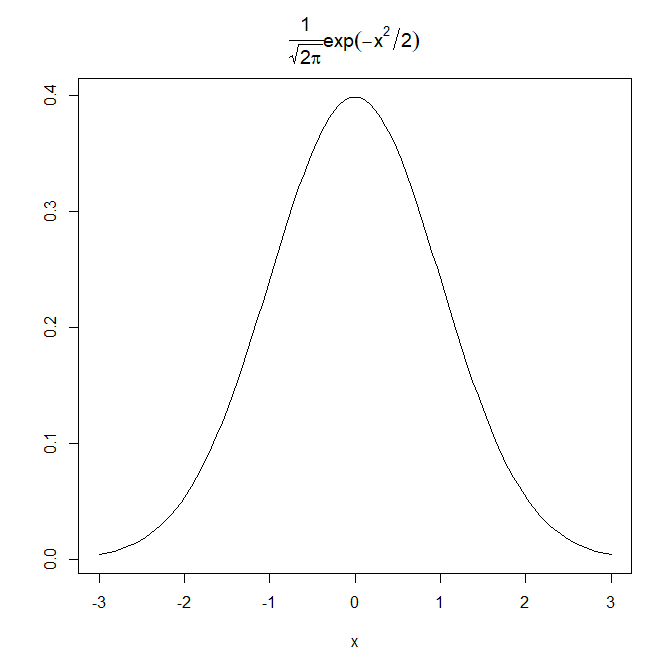
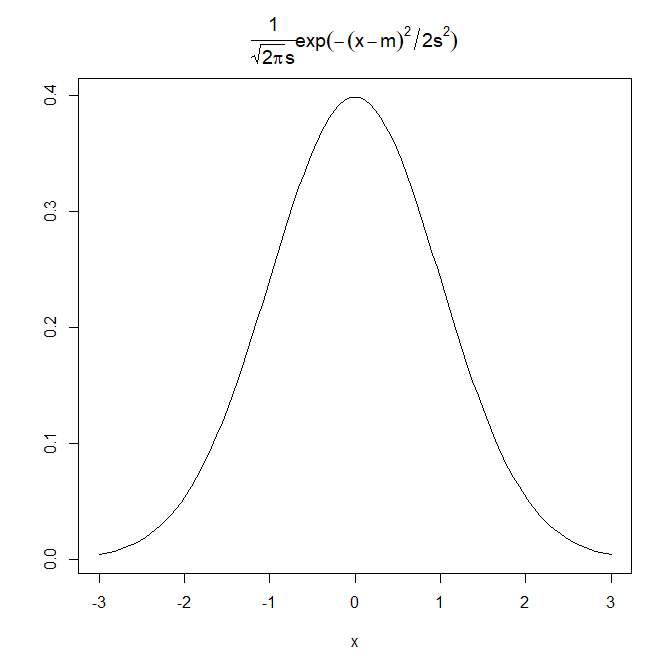
標準正規分布とはこういうものです。
標準正規分布ってのは平均が0で、幅がだいたい±3くらいまで広がっている形(分布)の事です。
標準偏差の説明はパスさせてください。
もしくは過去に95%信頼区間の記事を書いているのでそちらを見てください。
curve(dnorm(x), xlim=c(-3,3), ylab="",
main=expression(frac(1,sqrt(2*pi))*exp(-x^2/2)))
図中のタイトルの数式は標準正規分布の確率密度関数と呼ばれる式です。
Rの中にdnorm()というプログラム内の関数があります。
dはdensity(密度)のことで、normはnormal distribution(正規分布)の事です。
つまりdnormは正規分布の確率密度について定義されたプログラム内の関数という説明ができます。
図のような確率密度関数から確率を求めるには、微小区間を積分したら瞬間の確率が出ます。
積分したら確率が出るということは、面積が確率に相当しているということです。
確率は合計したら1になるものなので、全体の面積を積分すると1になるはずです。
数値積分はintegrate()で求められます。
integrate(dnorm,-Inf,Inf)
> integrate(dnorm,-Inf,Inf)
1 with absolute error < 9.4e-05
> integrate(dnorm,-3,3)
0.9973002 with absolute error < 9.3e-07
> integrate(dnorm,-2,2)
0.9544997 with absolute error < 1.8e-11
> integrate(dnorm,-1,1)
0.6826895 with absolute error < 7.6e-15
統計学で、正規分布に近似するデータの
「1σ区間は68割のデータがある」、
とか
「2σ見ていれば95%は説明できる」、
とかいうのは上記のことを言っています。
標準正規分布の確率密度関数とは
関数とは、何かxというデータが入ってきたら値f(x)を吐き出します。
y=axという式も**y=f(x)**として表現されます。
xというデータにaを掛け算した値を計算してくれる関数です。
式中expの後ろにxがあります。
expとは指数関数の事です。
expとはexponential:指数の略記です。
このexpも関数なのでf(x)です。
expとはe^xと表される式です。(eのx乗)
eとはネイピア数です。自然対数の底として使われます。
自然対数は今回どうでもいいです。
e = 2.718.....といった数の事です。
e^xと言われたら2.78^xという意味です。
piはパイです。
3.14です。
だいたい3です(ゆとり教育の賜物)。
ルートは平方根です。
0.5乗です。
1/2乗でもいいです。
以上をもとにアレルギーの出そうな数式を数字に変換すると、
前の項は
1/(2*3.14)^0.5 = 0.399
です。
後ろの項は、
2.78^(-x^2/2)
です。
つまり
0.399 * 2.78^(-1*x^2/2)
のxに何か数字を入れたら値が返ってくる関数だとわかりました。
数字を入れると図や式の意味が理解できるような気がします。
数字を入れてみる、f(x)を求める
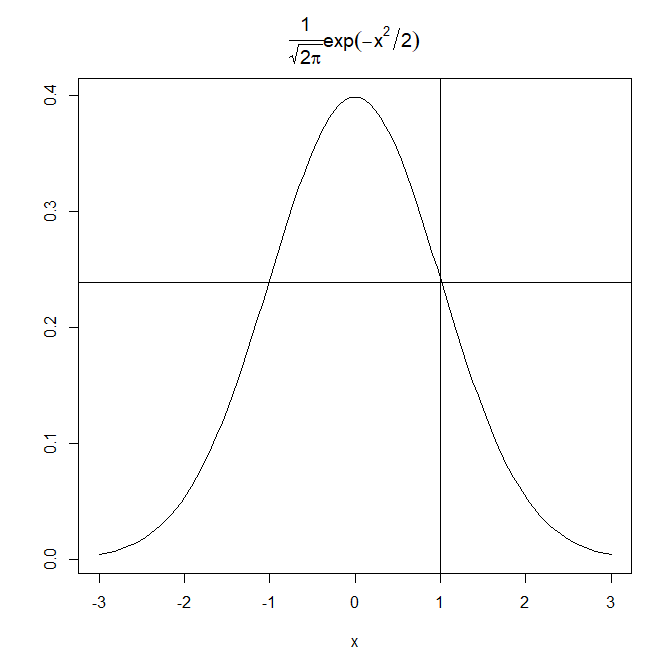
例えばxに1を代入します。
0.399 * 2.78^(-1*1^2/2) = 0.239
abline(h=0.239)
abline(v=1)
おお。こんな感じか。一致してます。
0を入れてみます。
0.399 * 2.78^(-1*0^2/2) = 0.399
そりゃそうですね。
-1*0は0ですし、
0/2は0です。
0乗は1ってのは決まりみたいに習うものでした。
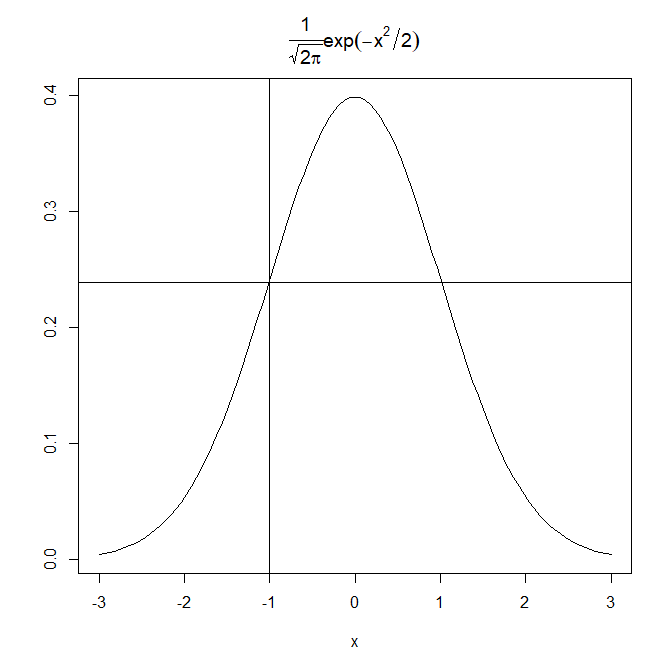
では-1を入れてみます
0.399 * 2.78^(-1*(-1)^2/2) = 0.239
二乗されることによってマイナスの効果は消えました。
abline(h=0.239)
abline(v=-1)
後ろの項について見てみる。
0から正の方向へ値を離していく。
> 2.78^(-1*(1)^2/2)
[1] 0.5997601
> 2.78^(-1*(2)^2/2)
[1] 0.1293929
> 2.78^(-1*(3)^2/2)
[1] 0.0100415
> 2.78^(-1*(4)^2/2)
[1] 0.000280312
徐々に減少しています。
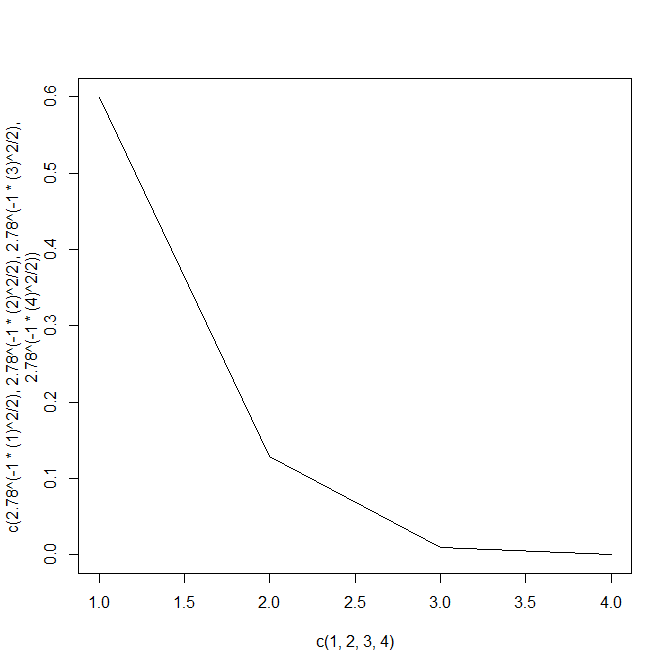
数字だけじゃ分からないので、図にしてみましょう。
plot(c(1,2,3,4),c(2.78^(-1*(1)^2/2),
2.78^(-1*(2)^2/2),
2.78^(-1*(3)^2/2),
2.78^(-1*(4)^2/2)),type="l")
0から離れるほど小さくなるが、傾斜は段々と緩やかになる。
0に徐々に近づく。
(0に漸近していく)
数字を入れていくことで標準正規分布の確率密度関数の動きは何となくわかりました。
数字を入れてわかったことは、
0.399(前の項)* 2.78^(-1*(-1)^2/2)(後ろの項)
から成り立っている式で、
xが0のとき最も大きい値をとり、0から1離れても-1離れても同じ値を取る。
正と負の方向に同じ距離離れていれば同じ値を返す。
だからplotすると山の形になる。
後ろの項を計算しながら確認したが、離れれば離れるほど傾斜は緩やかになる。
この性質のためにベルの形となる。
どんな時つかうの?
"正規分布に従う"とか、"サンプルサイズが大きければ正規分布に近似する"という言葉を聞く。
たとえば正規分布に従う数値の例には体重や身長がある。
体重や身長は取りうる値には限界がある。
サンプルサイズを1万として、一万人の身長を測定して平均を求める。
20歳男性の身長平均が170だったとすると、大多数の人は170±数センチに収まることは想像できるとおもう。
もちろん極めて高い身長の人や、低い身長の人も入ってきてはいるが少数であることは理解できる。
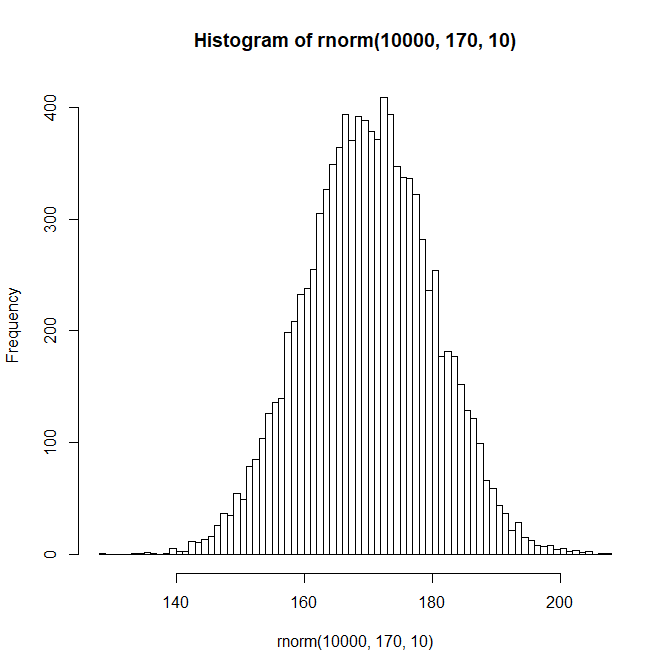
この身長についてヒストグラムを書くと以下のようになると考えられる。
hist(rnorm(10000,170,10),breaks=100)
正規分布に形が似ている。
(そりゃ正規分布から発生させた乱数だから、とは今は言わないでほしい)
たまに200とか130といった身長も観測されるが稀であるし、平均値に影響を及ぼすとも思えない。
ただ、少数ながら存在することを忘れてはならない。
つまり、130cmの20歳男性の存在する確率は?と聞かれたら、**極稀ながら存在する。**と答えられるためにも、
0に漸近するだけで0にはならない必要があるのです。
そのために(後ろの項)が働いてくれます。
でも身長って170が真中で0が真ん中ではないよね
身長の例では170が平均(山の頂点)であった。
標準正規分布は0が平均(山の頂点)であった。
"形が似ている"ということから"近似する"とは無理やり言えそう。
確率密度関数の良いところは積分すると確率になるところだった。
標準正規分布に従うデータがあったならば、-1から1の値が出てくる確率は?と聞かれたら
その範囲を積分したら0.68なので68%です。
と答えられる。
しかし、平均0と170ではそもそも値が違うし、ベルの広がり方も違う。
「20歳男性が167~168である確率は?」と聞かれたとて、
積分する対象の確率密度関数が分からないのでは求めようがない。
正規分布は標準化したら標準正規分布となる。
標準化とは、平均0標準偏差1に変換する行為である。
標準化とはデータ個々の値をデータ全体の平均で引き算し、
データの広がり具合である標準偏差で割ることで、データの広がりを抑える変換のことをいう。
(x-m)/s
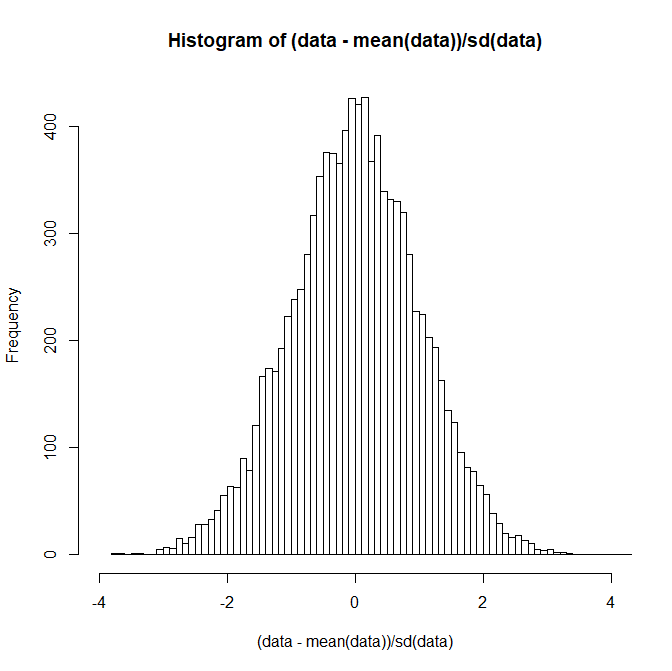
この処理を行うと、データは標準正規分布と極めて似た形になる。
data<-rnorm(10000,170,10)
hist((data-mean(data))/sd(data),breaks=100, xlim=c(-4,4))
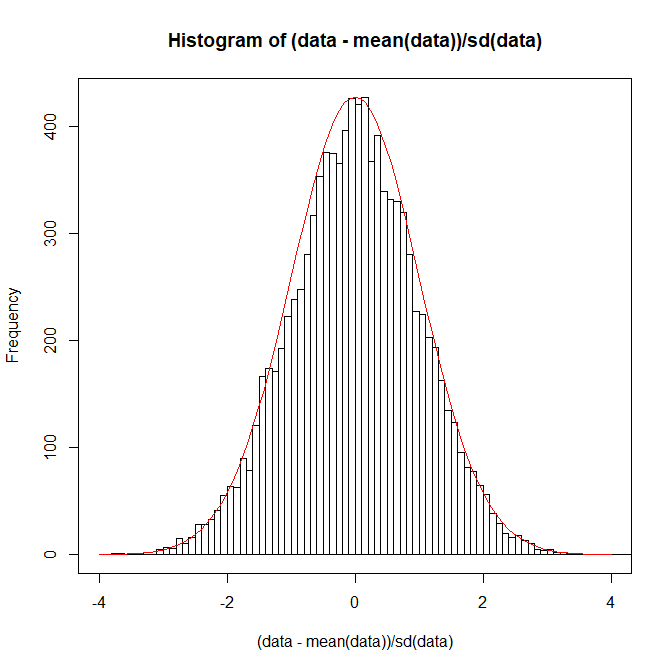
上からかぶせて確認してみよう
par(new=T)
curve(dnorm(x), xlim=c(-4,4), ylab="",xlab="",xaxt="n",yaxt="n",col="red")
全く似ていることが確認できた。
よって、身長というデータも、標準化することによって、
標準正規分布の確率密度関数と同じものを使って確率を出すことができるようになったわけだ。
でも標準化したことで元データが分かりにくくなった
平均が0になったということは、確率密度関数は標準正規分布のものを使うから確率が計算できるようになったとして、
「20歳男性が167~168である確率は?」と聞かれた時に、
標準化してしまったことによって、もはやx軸に167~168という数字は見当たらない。
どこからどこまでを積分したら167~168に相当するのかが分からなくなってしまった。
ならば標準正規分布の確率密度関数を、
標準化されてないがベル型で正規分布と言えそうなデータすべてに使える確率密度関数に変形してしまおう。
標準正規分布の確率密度関数が、平均0、標準偏差1のデータを想定していたなら
標準化の逆手順で元のデータに戻してやればいい。
つまり、引き算した平均値170を足して、割った標準偏差を掛け算してやる。
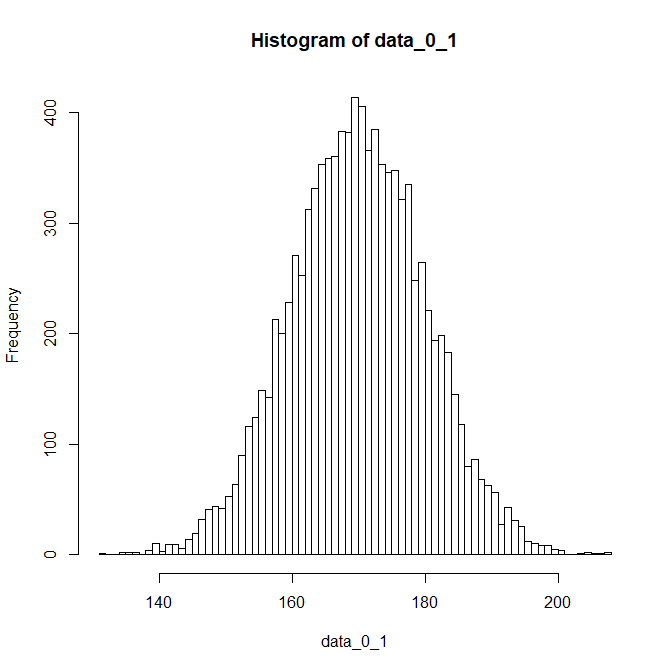
標準化を逆手順で戻す。
data_0_1 <- rnorm(10000,0,1)
data_0_1 <- (data_0_1* sd(data)) + mean(data)
hist(data_0_1,breaks=100)
平均0標準偏差1で発生させたデータに逆手順を行うとデータが身長のデータに似るようになった。
逆手順なので、先にデータに平均値を足し算してしまわないように。
後から標準偏差を掛け算すると数値が全く変わったものになるので注意。
このように、標準化されたデータは、平均値と標準偏差が分かれば自在なパラメータ(山の頂点や広がり)を持つ正規分布に変形できることがわかった。
標準正規分布の確率密度関数に変身してもらう
標準正規分布の確率密度関数にあるデータの入るxに少し手を加えて、変形してしまう。
平均値をmとして
標準偏差をsとする
curve(dnorm(x), xlim=c(-3,3), ylab="",
main=expression(frac(1,sqrt(2*pi)*s)*exp(-(x-m)^2/2*s^2)))
また前の項を考えます。
前の項はもともと0.399でした。
そこに標準偏差が割り算されます。
標準偏差10なら0.0399になります。
標準偏差はベルの幅に相当していました。
しかし、確率は合計して1です。ただ幅を広げるだけでは、確率が1を超えてしまいます。
そのため、ベルの幅を考えて前の項を小さくしているのです。
後ろの項を考えると、標準化と似ています。
xに入ってきた値から平均値mを引き算します。
xが160だとしたら、平均170との差は-10
180なら10となります。
その値の二乗を計算するので、符号はマイナスでもプラスでも構いません。
平均値からどれだけ離れているかを表しています。
ただ二乗すると、ほんとは平均値から10しか離れていなかったのに100という値が計算されてしまいます。
そこで分子の標準偏差も二乗したものを使います。
標準偏差が10であれば、分子は100になります。
よって、(x-m)^2 / s^2 = (160-170)^2 / 10^2 = 1 となります。
平均値から標準偏差一つ分離れた値は、標準偏差で割ると1になりました。
標準化と同じことが起こっています。
つまり、exp()の中身は標準化された値となるように処理されているのです。
後ろの項だけ計算してみましょう。
2.78^((-1/2)*((160-170)^2 / 10^2)) = 0.599
標準正規分布のときに計算した後ろの項と同じ値になりました。
> 2.78^((-1/2)*((160-170)^2 / 10^2))
[1] 0.5997601
> 2.78^((-1/2)*((150-170)^2 / 10^2))
[1] 0.1293929
> 2.78^((-1/2)*((140-170)^2 / 10^2))
[1] 0.0100415
標準偏差1つ分離していっても同じ値になりました。
つまり、上図中の式は、平均値や標準偏差をデータのパラメータあわせた関数と言える。
では数式で実装してみる
fxという関数を定義する
使うのはxというデータと、標準偏差、平均である。
fx<-function(x,SD,M) 1/(sqrt(2*pi)*SD)*(exp(-1*(x-M)^2/2/(SD^2)))
これで任意の平均や標準偏差にあわせた確率密度関数が定義できた。
一次元のデータがあったとする。
x1<-rnorm(1000,50,8)
SD1<-sd(x1)
M1<-mean(x1)
y<-rep(0,1000)
データの平均は50で、標準偏差は8だった。
このデータは正規分布に従うことが知られている。
このデータの確率密度関数は下図のようになる。
plot(x1,y,main=expression(frac(1,sqrt(2*pi)*8)*exp(-(x-50)^2/2%*%8^2)))
points(1,type="n")
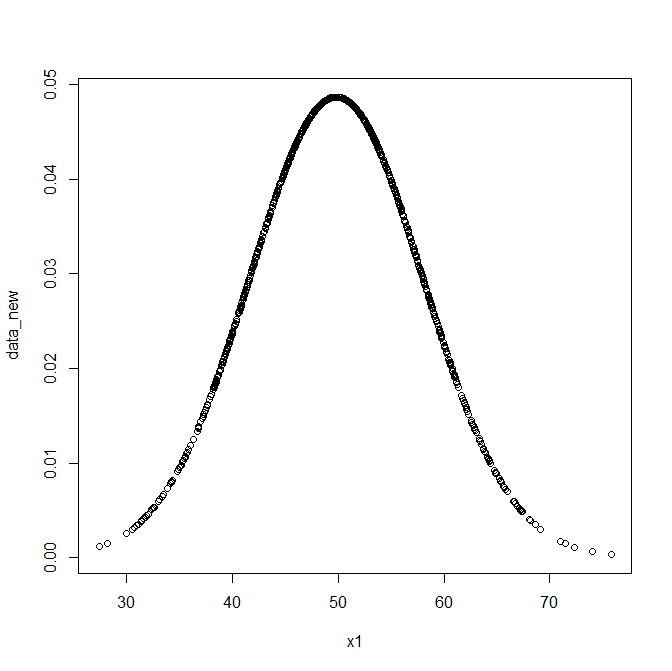
では確率密度関数によって計算された瞬間の確率値について定義した数式を使って計算してみる。
data_new<-fx(x1, SD1, M1)
plot(x1,data_new)
ベル型のカーブになったことがわかる。
50という平均値になる確率が最も高く表現され、
ベルの幅が標準偏差によって表現されていることがわかる。
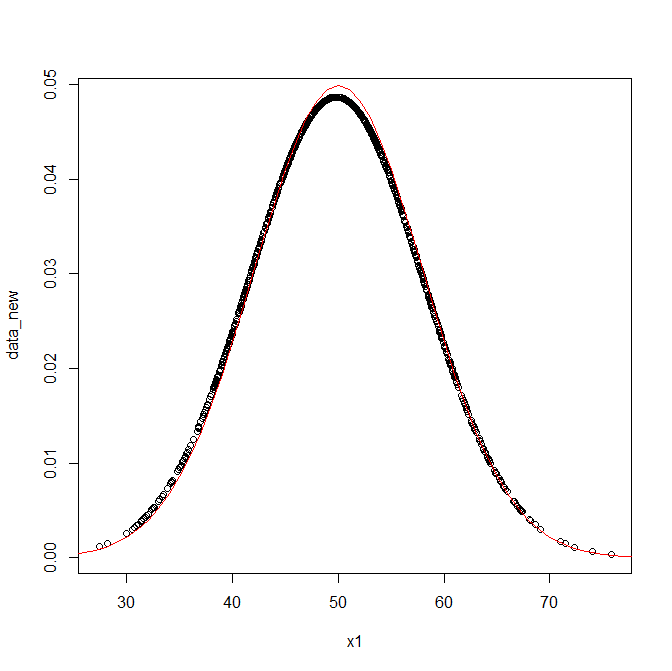
正しく実装できたのか、念のためRの組み込み関数dnorm()で上からplotして確認する。
curve(dnorm(x,50,8),0,100,add=T,col="red")
綺麗に重なっていることが確認できた。
正規分布を応用的につかう準備
この関数によって、xという値が変換され、yという値が新しくできた。
つまり、一次元のデータが二次元のデータになったと考えることができる。
df<-data.frame(fx=data_new, x = x1)
head(df)
fx x
1 0.035499955 43.45671
2 0.038963090 44.41898
3 0.046213558 53.27297
4 0.045358163 53.62315
5 0.033629041 57.17799
6 0.005808109 66.59357
平均に近い値は大きい値に、平均から遠い値は小さな値に変換してくれる関数ともとらえられる。
平均、標準偏差というパラメータがわかっていれば、どんなxが来ても変換してくれる。
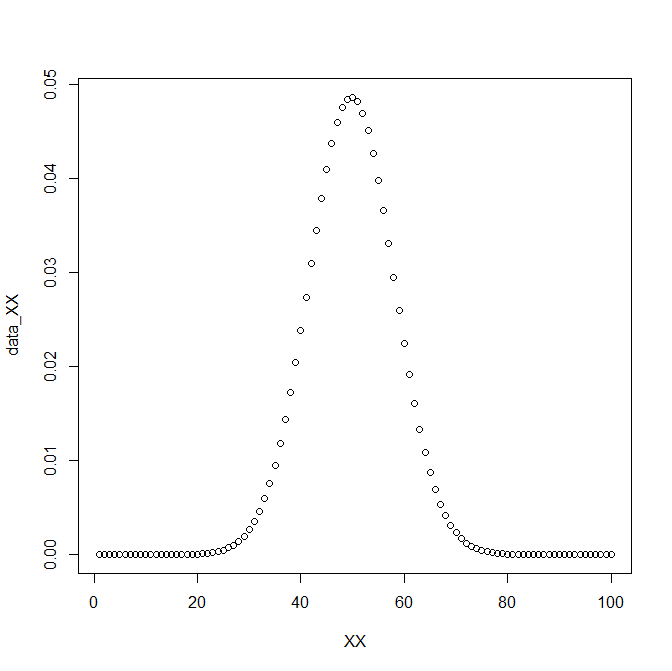
XX<-c(1:100)
data_XX<-fx(XX,SD1,M1)
plot(XX,data_XX)
たしかに変形してくれている。
> sum(data_XX)
[1] 1
合計はもちろん1となる。
(ただしsumを取る場合は、xが1刻みの想定である。seq(1,100,0.1)などで発生させた場合、0.1刻みなので合計値は10になる。)
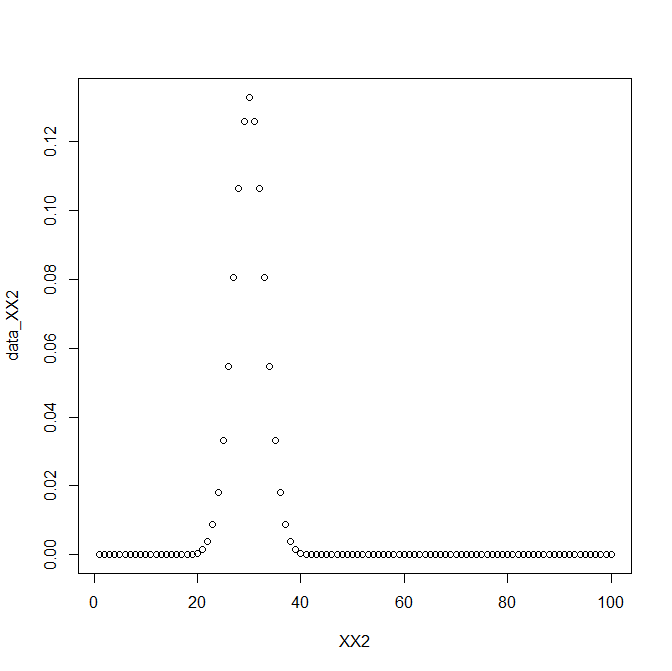
パラメータを変形したら、別の分布を書いてくれる。
XX2<-c(1:100)
data_XX2<-fx(XX2,3,30)
plot(XX2,data_XX2)
また違う形の正規分布にもフィットさせることができた。
以上
正規分布という存在や、確率密度関数は初めて見たときそっとテキストを閉じたが、
学習を進めるうちに逃げられないと悟り、ようやく最近慣れてきた。
正規分布の概念がわかると応用の幅は広く、カーネルトリック・ガウス過程回帰・異常検知にも使われる。
理解しておいて損はないし、なかなか(私のレベルで)わかりやすい解説が無かったので書くに至った。
今後の記事で応用していく。