0 はじめに
この記事では高速剰余変換と実装について解説していきます。この記事を書く上で参考にしたのはこのページです。
http://ushiro.jp/method/fmt.htm
http://www.cs.t-kougei.ac.jp/nsim/method/fmtbase.htm
基本的にはこのページで私が理解したとこ(+α)を解説します。多倍長整数の世界に興味のある方に少しでも面白さが伝わればと思い書きました。とか言ってますが私も全然素人です。ここではこの資料にのっとり高速剰余変換をFMT(Fast Modulo Transformation)と呼ぶこととします。 ←実は私がやってるのはNTT(数論変換)というようなものだったようで、詳しくは(FFTとNTTとFMTの違い)を見るとわかる通り剰余下でFFTやること=FMTではなかったようで私はずっと勘違いしていました。以下FMTはNTTと適宜読み替えてください。
1 なぜ高速剰余変換(FMT)が必要か
モチベーションの根底に「多数桁の円周率をプログラムで求めたい」というのがあります。円周率自体は小数ですが、実際の計算はほとんど多倍長整数を使って計算します。ここで「多倍長整数の乗算をいかに高速に行うか」がプログラム全体の速度に大きく影響します。普通、N桁の乗算は愚直にやると$O(N^{2})$の計算量でとても遅いですが、FMTを使えばおおむね$O(NlogN)$のオーダーまで速くなります。
なおただ単に円周率を計算するならGMP等のライブラリやy-cruncherがあるのですが、最初からこれを使ってしまっては面白みがないので今は考えないこととします。
2 FMTの簡易実装例
なにとはともあれこれで10進4桁の整数の乗算をしてみましょう。
Python3の簡易版FMT関数と逆FMT関数です。
import numpy as np
# MODP剰余下でaのb乗を返す
# 追記1:pow(a,b,MODP)を使ったほうが速い!
def ModExp(a, b):
ans = np.uint64(1)
aa = np.uint64(a)
while (b != 0):
if (b % 2 == 1):
ans = ans * aa % np.uint64(MODP)
aa = aa * aa % np.uint64(MODP)
b //= 2
return np.uint32(ans)
# bit逆順 uint型を想定
def bitRev(a):
a = (a & 0x55555555) << 1 | (a & 0xAAAAAAAA) >> 1
a = (a & 0x33333333) << 2 | (a & 0xCCCCCCCC) >> 2
a = (a & 0x0F0F0F0F) << 4 | (a & 0xF0F0F0F0) >> 4
a = (a & 0x00FF00FF) << 8 | (a & 0xFF00FF00) >> 8
a = (a & 0x0000FFFF) << 16 | (a & 0xFFFF0000) >> 16
return a >> (32 - digit_level)
def FMT(inputA):
# まず配列をビット逆順
arrayA = inputA[bitRev(np.uint32(range(digitN)))]
# FMTループ
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = ModExp(MODP_Wn, t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(MODP))
arrayA[t1] = (arrayAt0 + MODP - w1) % MODP
arrayA[t0] = (arrayAt0 + w1) % MODP
return arrayA[:]
def iFMT(inputA):
# まず配列をビット逆順
arrayA = inputA[bitRev(np.uint32(range(digitN)))]
# FMTループ
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = ModExp(MODP_Wn, digitN - t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(MODP))
arrayA[t1] = (arrayAt0 + MODP - w1) % MODP
arrayA[t0] = (arrayAt0 + w1) % MODP
return arrayA[:]
def DivN(inputA):
digitN_r = ModExp(digitN, MODP - 2) # digitNのモジュラ逆数を計算
ret = np.uint64(inputA[:]) * np.uint64(digitN_r) % np.uint64(MODP)
return np.uint32(ret)
if __name__=="__main__":
# 可変パラメーター
digit_level = 3
digitN = 1 << digit_level
MODP = np.uint32(257)
MODP_Wn = np.uint32(4) # 1の原始N乗根でなければならない。4の8乗=65536。65536%257=1
# C=A*Bをしたい
A=np.uint32([1,4,1,4,0,0,0,0])
B=np.uint32([2,1,3,5,0,0,0,0])
A = FMT(A) # 変換
B = FMT(B) # 変換
C = np.uint64(A[:]) * np.uint64(B[:]) % np.uint64(MODP) # 各要素どうし乗算
C = np.uint32(C)
C = iFMT(C) # 逆変換
C = DivN(C) # Nで割る
print("畳み込みの結果")
for i in range(digitN):
print("C[",i,"] =",C[i])
A,B各要素に10進1桁が入っています。ここでは
A=np.uint32([1,4,1,4,0,0,0,0])
B=np.uint32([2,1,3,5,0,0,0,0])
としているので4141*5312の計算をしようとしています。答えは21996992となるはずです。
畳み込みの結果
C[ 0 ] = 2
C[ 1 ] = 9
C[ 2 ] = 9
C[ 3 ] = 26
C[ 4 ] = 27
C[ 5 ] = 17
C[ 6 ] = 20
C[ 7 ] = 0
C[0]が1の位、C[1]が10の位・・・で畳み込みの結果が出力されています。
まだ繰り上がりの計算をしていませんので、計算すると
C[ 0 ] = 2
C[ 1 ] = 9
C[ 2 ] = 9
C[ 3 ] = 6
C[ 4 ] = 9
C[ 5 ] = 9
C[ 6 ] = 1
C[ 7 ] = 2
2・1・9・9・6・9・9・2
あってます!
次は1234*5678をやってみます。答えは7006652になるはずです。
畳み込みの結果
C[ 0 ] = 32
C[ 1 ] = 52
C[ 2 ] = 61
C[ 3 ] = 60
C[ 4 ] = 34
C[ 5 ] = 16
C[ 6 ] = 5
C[ 7 ] = 0
繰り上がり処理の結果
C[ 0 ] = 2
C[ 1 ] = 5
C[ 2 ] = 6
C[ 3 ] = 6
C[ 4 ] = 0
C[ 5 ] = 0
C[ 6 ] = 7
C[ 7 ] = 0
7・0・0・6・6・5・2
あってます!
面白いですね。
次は9999*9999をやってみます。
畳み込みの結果
C[ 0 ] = 81
C[ 1 ] = 162
C[ 2 ] = 243
C[ 3 ] = 67
C[ 4 ] = 243
C[ 5 ] = 162
C[ 6 ] = 81
C[ 7 ] = 0
繰り上がり処理の結果
C[ 0 ] = 1
C[ 1 ] = 0
C[ 2 ] = 0
C[ 3 ] = 3
C[ 4 ] = 2
C[ 5 ] = 7
C[ 6 ] = 9
C[ 7 ] = 9
答えは99980001になるはずですが、残念ながら違った結果がでています。
この簡易版FMTでは法$P=257$としており、すべての計算は257の剰余下で行われています。本当は畳み込み結果C[3]が324のところを67にされているのが原因です。剰余版オーバーフローみたいなもんです。
ここで少しFMT関数が何をしているかを説明します。
FMT関数はaを入力としてこのようなfを出力しています。
$f_k=a_0ω^{0}+a_1ω^{k}+a_2ω^{2k}....+a_{n-1}ω^{(n-1)k}$
(k=0,1,2・・・・n-1)
$ω$は適当な整数とし、$ω^{n}≡1$ $(mod$ $P)$となるPの剰余下で計算をします。$ω$と$P$は互いに素な必要があります。これにより$ω^1,ω^2,ω^3・・$は$ω^n$まで同じ数が出現せず、$ω^n$でちょうど1周回ってくる性質のためFFTと同じくバラフライ演算ができ、FFTと同様高速に計算できるのです。逆変換は$ω$を$-ω$に置き換えるだけです(ただし最後全体をNで割るのはFFTと同じ)。
FFTでは小数や複素数で計算を進めていきますが、これを全て整数でやることで小数特有の誤差を気にする必要がなくなります。ただ先ほど述べたように全ての計算を整数剰余下で行うので音声信号の周波数を求めたりする用途等には使われず、多倍長整数の乗算や競プロの問題に利用される程度で、FFTと比べたら用途は狭いようです。
多倍長整数の乗算を行うためには上記のコードのように
A,BをFMTで変換
↓
変換後のA,Bの各要素同士を乗算
↓
FMT逆変換
をすることで、畳み込み結果を得ることができます。
畳み込み結果もmod Pされているので、畳み込み結果がP以上になる可能性がある場合、計算が正しく行えません。なのでP自体を大きくするか、複数のPを使って剰余下の結果を得た後、中国余剰定理で復元するしかありません。基本的には後者のアプローチをとることが多いです。
参考
【FFT,FMTで$O(NlogN$)で畳み込みできる原理】
https://qiita.com/peria/items/fbdd52768b4659823d88
2-1 Pを大きくとるアプローチ
とりあえず257は小さすぎるので$P=65537$でやってみます。ソースコードのMODPとMODP_Wnを以下に書き換えます。
MODP = 65537
MODP_Wn = 16
これでやると
畳み込みの結果
C[ 0 ] = 81
C[ 1 ] = 162
C[ 2 ] = 243
C[ 3 ] = 324
C[ 4 ] = 243
C[ 5 ] = 162
C[ 6 ] = 81
C[ 7 ] = 0
繰り上がり処理の結果
C[ 0 ] = 1
C[ 1 ] = 0
C[ 2 ] = 0
C[ 3 ] = 0
C[ 4 ] = 8
C[ 5 ] = 9
C[ 6 ] = 9
C[ 7 ] = 9
99980001
あってます。
しかし、ただPを大きくするのでは限界があります。もっと大きい桁数で計算することを考えるとPの必要最低桁数は2進64桁以上になりそうで、いよいよ剰余計算自体がlong型でも扱えなくなってしまいます。
2-2 中国余剰定理を使ったアプローチ
Pを257と17でやってみましょう
import numpy as np
# MODP剰余下でaのb乗を返す
# 追記1:np.uint32(pow(np.uint32(a),np.uint32(b),np.uint32(MODP)))を使ったほうが速い!
def ModExp(a, b):
ans = np.uint64(1)
aa = np.uint64(a)
while (b != 0):
if (b % 2 == 1):
ans = ans * aa % np.uint64(MODP)
aa = aa * aa % np.uint64(MODP)
b //= 2
return np.uint32(ans)
# aの逆元を返す mod m
def modinv(a,m):
b = m
u = 1
v = 0
while (b) :
t = a // b
a -= t * b
tmp=a
a=b
b=tmp
u -= t * v
tmp = u
u = v
v = tmp
u %= m
if u < 0:
u += m
return u
# bit逆順 uint型を想定
def bitRev(a):
a = (a & 0x55555555) << 1 | (a & 0xAAAAAAAA) >> 1
a = (a & 0x33333333) << 2 | (a & 0xCCCCCCCC) >> 2
a = (a & 0x0F0F0F0F) << 4 | (a & 0xF0F0F0F0) >> 4
a = (a & 0x00FF00FF) << 8 | (a & 0xFF00FF00) >> 8
a = (a & 0x0000FFFF) << 16 | (a & 0xFFFF0000) >> 16
return a >> (32 - digit_level)
def FMT(inputA):
# まず配列をビット逆順
arrayA = inputA[bitRev(np.uint32(range(digitN)))]
# FMTループ
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = ModExp(MODP_Wn, t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(MODP))
arrayA[t1] = (arrayAt0 + MODP - w1) % MODP
arrayA[t0] = (arrayAt0 + w1) % MODP
return arrayA[:]
def iFMT(inputA):
# まず配列をビット逆順
arrayA = inputA[bitRev(np.uint32(range(digitN)))]
# FMTループ
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = ModExp(MODP_Wn, digitN - t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(MODP))
arrayA[t1] = (arrayAt0 + MODP - w1) % MODP
arrayA[t0] = (arrayAt0 + w1) % MODP
return arrayA[:]
def DivN(inputA):
digitN_r = modinv(digitN, int(MODP)) # digitNの逆元を計算
ret = np.uint64(inputA[:]) * np.uint64(digitN_r) % np.uint64(MODP)
return np.uint32(ret)
if __name__=="__main__":
digit_level = 3
digitN = 1 << digit_level
# C=A*Bをしたい
A_=np.uint32([9,9,9,9,0,0,0,0])
B_=np.uint32([9,9,9,9,0,0,0,0])
#まずp=257でやる
MODP = np.uint32(257)
MODP_Wn = np.uint32(4) # 1の原始N乗根でなければならない。4の8乗=65536。65536%257=1
A = FMT(A_) # 変換
B = FMT(B_) # 変換
C0 = np.uint64(A[:]) * np.uint64(B[:]) % np.uint64(MODP) # 各要素どうし乗算
C0 = np.uint32(C0)
C0 = iFMT(C0) # 逆変換
C0 = DivN(C0) # Nで割る
#p=17でやる
MODP = np.uint32(17)
MODP_Wn = np.uint32(2) # 1の原始N乗根でなければならない。2の8乗=256。256%17=1
A = FMT(A_) # 変換
B = FMT(B_) # 変換
C1 = np.uint64(A[:]) * np.uint64(B[:]) % np.uint64(MODP) # 各要素どうし乗算
C1 = iFMT(C1) # 逆変換
C1 = DivN(C1) # Nで割る
print("畳み込みの結果 mod","257","\t\t畳み込みの結果 mod","17","\t\tGarnerで復元")
for i in range(digitN):
print("C[",i,"] =",C0[i],
" \t\t\t\t","C[",i,"] =",C1[i],
"\t\t\t\t",int(C0[i])+((int(C1[i])-int(C0[i]))*modinv(257,17))%17*257
)
実行結果↓
畳み込みの結果 mod 257 畳み込みの結果 mod 17 Garnerで復元
C[ 0 ] = 81 C[ 0 ] = 13 81
C[ 1 ] = 162 C[ 1 ] = 9 162
C[ 2 ] = 243 C[ 2 ] = 5 243
C[ 3 ] = 67 C[ 3 ] = 1 324
C[ 4 ] = 243 C[ 4 ] = 5 243
C[ 5 ] = 162 C[ 5 ] = 9 162
C[ 6 ] = 81 C[ 6 ] = 13 81
C[ 7 ] = 0 C[ 7 ] = 0 0
ここではGarnerのアルゴリズムというのを使って復元しています。ちゃんとC[3]が324になってますね!復元したものを繰り上がり処理すれば
99980001
が得られます。
Garnerアルゴリズムについて超ざっくり説明すると、復元したいxがあって
x%a が ar
x%b が br
のとき
ar+(br-ar)*modinv(a,b)%b*a
でもとの値が復元できるというアルゴリズムです。modinvは「aをかけるとbの剰余下で1になる整数」を返す関数です。
Garnerのアルゴリズムはわかりやすいサイトがいくつもあるのでそちらをご参照ください。
https://www.creativ.xyz/ect-gcd-crt-garner-927/
https://qiita.com/drken/items/ae02240cd1f8edfc86fd
他にも拡張ユークリッド互除法で値を復元することもでき、それを使ってもいいと思います。
このようにPの値自体を大きくせずとも、使うPの種類を増やしていけば大きな数を復元できることがわかります。
3 大きめの桁に挑戦
3-1 1要素に32bit敷き詰める
今までわかりやすさ優先で10進法前提でやっていましたが4294967296進法(=2の32乗)で多倍長乗算をやりたいと思います。
A=np.uint32([4294967295,4294967295,4294967295,4294967295,0,0,0,0])
B=np.uint32([4294967295,4294967295,4294967295,4294967295,0,0,0,0])
入力側を32bit敷き詰めました。右半分はまだ0ですがこれもあとで使えるようになります。
このまま動かすとGarnerで復元できる257*17を大幅に超えるので法Pも大きくします。
MODPを469762049 , 1811939329 , 2013265921
MODP_Wnを443138433 , 1452317833 , 1801542727
とします。
あと「FMT→同じ要素同士乗算→iFMT→Nで割る」の一連の操作をComvolution関数にまとめて全体をクラス化します。
import numpy as np
# aの逆元を返す mod m
def modinv(a,m):
b = m
u = 1
v = 0
while (b) :
t = a // b
a -= t * b
tmp=a
a=b
b=tmp
u -= t * v
tmp = u
u = v
v = tmp
u %= m
if u < 0:
u += m
return u
# bit逆順 uint型を想定
def bitRev(a):
a = (a & 0x55555555) << 1 | (a & 0xAAAAAAAA) >> 1
a = (a & 0x33333333) << 2 | (a & 0xCCCCCCCC) >> 2
a = (a & 0x0F0F0F0F) << 4 | (a & 0xF0F0F0F0) >> 4
a = (a & 0x00FF00FF) << 8 | (a & 0xFF00FF00) >> 8
a = (a & 0x0000FFFF) << 16 | (a & 0xFFFF0000) >> 16
return a >> (32 - digit_level)
# garnerのアルゴリズム、3変数ver
# 64bit整数におさまらない可能性あり、pythonのint型を使用
def Garner(a_,b_,c_,ar_,br_,cr_):
a = int(a_)
b = int(b_)
c = int(c_)
ar = int(ar_)
br = int(br_)
cr = int(cr_)
x = ar + (br - ar) * modinv(a,b) % b * a
x = x + (cr - x % c) * modinv(a,c) % c * modinv(b,c) % c * a * b
#x %= a*b*c #a<b<cのときこの処理は必要ない
return x
class FMTClass():
def __init__(self,MODP,MODP_Wn):
self.MODP=np.uint32(MODP)
self.MODP_Wn=np.uint32(MODP_Wn)
# MODP剰余下でaのb乗を返す
# 追記1:np.uint32(pow(np.uint32(a),np.uint32(b),np.uint32(self.MODP)))を使ったほうが速い!
def ModExp(self,a, b):
ans = np.uint64(1)
aa = np.uint64(a)
while (b != 0):
if (b % 2 == 1):
ans = ans * aa % np.uint64(self.MODP)
aa = aa * aa % np.uint64(self.MODP)
b //= 2
return np.uint32(ans)
def FMT(self,inputA):
# まず配列をビット逆順
arrayA = inputA[bitRev(np.uint32(range(digitN)))]
# FMTループ
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = self.ModExp(self.MODP_Wn, t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(self.MODP))
arrayA[t1] = (arrayAt0 + self.MODP - w1) % self.MODP
arrayA[t0] = (arrayAt0 + w1) % self.MODP
return arrayA[:]
def iFMT(self,inputA):
# まず配列をビット逆順
arrayA = inputA[bitRev(np.uint32(range(digitN)))]
# FMTループ
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = self.ModExp(self.MODP_Wn, digitN - t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(self.MODP))
arrayA[t1] = (arrayAt0 + self.MODP - w1) % self.MODP
arrayA[t0] = (arrayAt0 + w1) % self.MODP
return arrayA[:]
def DivN(self,inputA):
digitN_r = modinv(digitN, int(self.MODP)) # digitNの逆元を計算
ret = np.uint64(inputA[:]) * np.uint64(digitN_r) % np.uint64(self.MODP)
return np.uint32(ret)
#A*Bの畳み込み結果を返す
def Convolution(self,A_,B_):
A = self.FMT(A_%self.MODP)
B = self.FMT(B_%self.MODP)
C = np.uint64(A[:]) * np.uint64(B[:]) % np.uint64(self.MODP) # 各要素どうし乗算
C = np.uint32(C) #結果は32bit範囲内におさまってるので
C = self.iFMT(C) # 逆変換
C = self.DivN(C) # Nで割る
return C
if __name__=="__main__":
digit_level = 3
digitN = 1 << digit_level
FMT_P0 = FMTClass(MODP=469762049 , MODP_Wn=443138433)
FMT_P1 = FMTClass(MODP=1811939329, MODP_Wn=1452317833)
FMT_P2 = FMTClass(MODP=2013265921, MODP_Wn=1801542727)
# C=A*Bをしたい
A_=np.uint32([4294967295,4294967295,4294967295,4294967295,0,0,0,0])
B_=np.uint32([4294967295,4294967295,4294967295,4294967295,0,0,0,0])
#p=469762049でやる
C0 = FMT_P0.Convolution(A_,B_)
#p=1811939329でやる
C1 = FMT_P1.Convolution(A_, B_)
#p=2013265921でやる
C2 = FMT_P2.Convolution(A_, B_)
print("畳み込みの結果 mod","469762049",
"\t\t畳み込みの結果 mod","1811939329",
"\t\t畳み込みの結果 mod", "2013265921",
"\t\tGarnerで復元")
for i in range(digitN):
print("C[",i,"] =",C0[i],
" \t\t\t\t", "C[", i, "] =", C1[i],
" \t\t\t\t", "C[", i, "] =", C2[i],
"\t\t\t\t",Garner(FMT_P0.MODP,FMT_P1.MODP,FMT_P2.MODP,C0[i],C1[i],C2[i])
)
結果は
畳み込みの結果 mod 469762049 畳み込みの結果 mod 1811939329 畳み込みの結果 mod 2013265921 Garnerで復元
C[ 0 ] = 325957443 C[ 0 ] = 1429170264 C[ 0 ] = 635297256 18446744065119617025
C[ 1 ] = 182152837 C[ 1 ] = 1046401199 C[ 1 ] = 1270594512 36893488130239234050
C[ 2 ] = 38348231 C[ 2 ] = 663632134 C[ 2 ] = 1905891768 55340232195358851075
C[ 3 ] = 364305674 C[ 3 ] = 280863069 C[ 3 ] = 527923103 73786976260478468100
C[ 4 ] = 38348231 C[ 4 ] = 663632134 C[ 4 ] = 1905891768 55340232195358851075
C[ 5 ] = 182152837 C[ 5 ] = 1046401199 C[ 5 ] = 1270594512 36893488130239234050
C[ 6 ] = 325957443 C[ 6 ] = 1429170264 C[ 6 ] = 635297256 18446744065119617025
C[ 7 ] = 0 C[ 7 ] = 0 C[ 7 ] = 0 0
検算してみましょう。
# 愚直に計算
import numpy as np
A_ = np.uint32([4294967295, 4294967295, 4294967295, 4294967295, 0, 0, 0, 0])
B_ = np.uint32([4294967295, 4294967295, 4294967295, 4294967295, 0, 0, 0, 0])
A=0
B=0
r=1
for i in range(8):
A += int(A_[i]) * r
B += int(B_[i]) * r
r*=2**32
print(A*B)
# FMTの答え
C_=[18446744065119617025,36893488130239234050,55340232195358851075,73786976260478468100,55340232195358851075,36893488130239234050,18446744065119617025,0]
C=0
r=1
for i in range(8):
C+=C_[i]*r
r*=2**32
print(C)
結果は
115792089237316195423570985008687907852589419931798687112530834793049593217025
115792089237316195423570985008687907852589419931798687112530834793049593217025
あってました!嬉しいですね!
これで4294967296進数で多倍長整数の乗算ができるようになりました。np.uint32型に32bit敷き詰めることができて気持ちいいです。また、Garnerで復元するところ以外は、計算は全て64bit整数の範囲内におさまっています。Garnerで復元するところはどうしても64bit整数をオーバーするので「Python3のint型」を使っています(Python3のint型は実質多倍長整数)。ここはGPU(CUDA)に移植する際には少し考えないといけなさそうですね。
3-2 A,Bの要素数を増やす
今までわかりやすさ優先でAとBを8要素でやっていましたが、もっと増やしてみたいと思います。要素数が$2^N$ならなんでも良い・・・と言いたいところですが、前述のよう$ω^n≡1$ $(mod$ $P)$という条件があります。
先ほどMODPを$469762049$ , $1811939329$ , $2013265921$
MODP_Wnを$443138433$ , $1452317833$ , $1801542727$
としていましたが、それぞれ
$443138433^8≡1$ $(mod$ $469762049)$
$1452317833^8≡1$ $(mod$ $1811939329)$
$1801542727^8≡1$ $(mod$ $2013265921)$
が成りたっていました。
$443138433$は$8$乗すると$469762049$剰余下で$1$になるので$443138433$は$1$の原始$8$乗根と言います。
要素数を$2^N$にしたいのであれば、1の原始$2^N$乗根とPを用意しなければいけませんが、ここでその例をいくつかあげてみます。
$52278$は$2013265921$を法としたとき、$1$の原始$2^{27}$乗根
$60733$は$469762049$を法としたとき、$1$の原始$2^{26}$乗根
$59189$は$1811939329$を法としたとき、$1$の原始$2^{26}$乗根
です。
ちょうどいいのでこれを使います。これでいっきに要素数を$2^{26}$まで増やして、1億桁近くの多倍長乗算ができます!
と、思ってやってみたらさすがに重くて結果が出るまで2日かかりました。やっぱりPythonは遅いですね()。数十秒で終わるように要素数を$2^{14}$に抑えたバージョンを貼ります。
import numpy as np
# aの逆元を返す mod m
def modinv(a,m):
b = m
u = 1
v = 0
while (b) :
t = a // b
a -= t * b
tmp=a
a=b
b=tmp
u -= t * v
tmp = u
u = v
v = tmp
u %= m
if u < 0:
u += m
return u
# bit逆順 uint型を想定
def bitRev(a):
a = (a & 0x55555555) << 1 | (a & 0xAAAAAAAA) >> 1
a = (a & 0x33333333) << 2 | (a & 0xCCCCCCCC) >> 2
a = (a & 0x0F0F0F0F) << 4 | (a & 0xF0F0F0F0) >> 4
a = (a & 0x00FF00FF) << 8 | (a & 0xFF00FF00) >> 8
a = (a & 0x0000FFFF) << 16 | (a & 0xFFFF0000) >> 16
return a >> (32 - digit_level)
# garnerのアルゴリズム、3変数ver
# 64bit整数におさまらない可能性あり、pythonのint型を使用
def Garner(a_,b_,c_,ar_,br_,cr_):
a = int(a_)
b = int(b_)
c = int(c_)
ar = int(ar_)
br = int(br_)
cr = int(cr_)
x = ar + (br - ar) * modinv(a,b) % b * a
x = x + (cr - x % c) * modinv(a,c) % c * modinv(b,c) % c * a * b
#x %= a*b*c #a<b<cのときこの処理は必要ない
return x
class FMTClass():
def __init__(self,MODP,MODP_Wn):
self.MODP=np.uint32(MODP)
self.MODP_Wn=np.uint32(MODP_Wn)
# MODP剰余下でaのb乗を返す
# 追記1:np.uint32(pow(np.uint32(a),np.uint32(b),np.uint32(self.MODP)))を使ったほうが速い!
def ModExp(self,a, b):
ans = np.uint64(1)
aa = np.uint64(a)
while (b != 0):
if (b % 2 == 1):
ans = ans * aa % np.uint64(self.MODP)
aa = aa * aa % np.uint64(self.MODP)
b //= 2
return np.uint32(ans)
def FMT(self,inputA):
# まず配列をビット逆順
arrayA = inputA[bitRev(np.uint32(range(digitN)))]
# FMTループ
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = self.ModExp(self.MODP_Wn, t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(self.MODP))
arrayA[t1] = (arrayAt0 + self.MODP - w1) % self.MODP
arrayA[t0] = (arrayAt0 + w1) % self.MODP
return arrayA[:]
def iFMT(self,inputA):
# まず配列をビット逆順
arrayA = inputA[bitRev(np.uint32(range(digitN)))]
# FMTループ
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = self.ModExp(self.MODP_Wn, digitN - t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(self.MODP))
arrayA[t1] = (arrayAt0 + self.MODP - w1) % self.MODP
arrayA[t0] = (arrayAt0 + w1) % self.MODP
return arrayA[:]
def DivN(self,inputA):
digitN_r = modinv(digitN, int(self.MODP)) # digitNの逆元を計算
ret = np.uint64(inputA[:]) * np.uint64(digitN_r) % np.uint64(self.MODP)
return np.uint32(ret)
#A*Bの畳み込み結果を返す
def Convolution(self,A_,B_):
A = self.FMT(A_%self.MODP)
B = self.FMT(B_%self.MODP)
C = np.uint64(A[:]) * np.uint64(B[:]) % np.uint64(self.MODP) # 各要素どうし乗算
C = np.uint32(C) #結果は32bit範囲内におさまってるので
C = self.iFMT(C) # 逆変換
C = self.DivN(C) # Nで割る
return C
# 検算用。A,Bの配列から一つの多倍長整数を作る。pythonのint型は乗算にKaratsuba法を使っているのでちょっと速い
def CalcAB(A,B):
Alist = A.tolist()
Blist = B.tolist()
r=2**32
for i in range(digit_level):
for j in range(2**(digit_level-1-i)):
Alist[j] = Alist[j * 2] + Alist[j * 2 + 1] * r
Blist[j] = Blist[j * 2] + Blist[j * 2 + 1] * r
r = r * r
return Alist[0] * Blist[0]
# 検算用。Cから一つの多倍長整数を作る
def CalcC(C):
Clist = C.tolist()
r = 2 ** 32
for i in range(digit_level):
for j in range(2 ** (digit_level-1 - i)):
Clist[j] = Clist[j * 2] + Clist[j * 2 + 1] * r
r = r * r
return Clist[0]
def CreateWn(a,m,n_level):
ans=a
for i in range(n_level-digit_level):
ans=ans*ans%m
return ans
# E0,E1,E2を使ってgarnerでEを復元して繰り上がり処理
def Carrying(C0,C1,C2):
C = np.zeros(digitN).astype(np.uint32)
upg = 0 # 繰り上がり分 python3のint型なのでオーバーフローの心配はない
for i in range(digitN):
g = Garner(FMT_P0.MODP, FMT_P1.MODP, FMT_P2.MODP, C0[i], C1[i], C2[i])
g += upg
C[i] = np.uint32(g % 4294967296)
upg = g//4294967296
return C
if __name__=="__main__":
digit_level = 14
digitN = 1 << digit_level
FMT_P0 = FMTClass(MODP=469762049 , MODP_Wn=CreateWn(60733,469762049,26))
FMT_P1 = FMTClass(MODP=1811939329, MODP_Wn=CreateWn(59189,1811939329,26))
FMT_P2 = FMTClass(MODP=2013265921, MODP_Wn=CreateWn(52278,2013265921,27))
# C=A*Bをしたい
# A,Bの初期化。前半にランダムな値をいれる。あとは0
A_ = np.zeros(digitN).astype(np.uint32)
A_[0:digitN // 2] = np.uint32( np.random.randint(0, 2147483648, (digitN // 2)) * 2
+ np.random.randint(0, 2, (digitN // 2)))
B_ = np.zeros(digitN).astype(np.uint32)
B_[0:digitN // 2] = np.uint32(np.random.randint(0, 2147483648, (digitN // 2)) * 2
+ np.random.randint(0, 2, (digitN // 2)))
#p=469762049でやる
C0 = FMT_P0.Convolution(A_,B_)
#p=1811939329でやる
C1 = FMT_P1.Convolution(A_, B_)
#p=2013265921でやる
C2 = FMT_P2.Convolution(A_, B_)
#一部結果表示
print("畳み込みの結果 mod","469762049",
"\t\t畳み込みの結果 mod","1811939329",
"\t\t畳み込みの結果 mod", "2013265921",
"\t\tGarnerで復元")
for i in range(10):
print("C[",i,"] =",C0[i],
" \t\t\t\t", "C[", i, "] =", C1[i],
" \t\t\t\t", "C[", i, "] =", C2[i],
"\t\t\t\t",Garner(FMT_P0.MODP,FMT_P1.MODP,FMT_P2.MODP,C0[i],C1[i],C2[i])
)
#繰り上がり
C=Carrying(C0,C1,C2)
#検算
print("検算開始")
if CalcAB(A_, B_)==CalcC(C):
print("正解!")
else:
print("ちがう!")
なんだか検算のほうが速かった気がします・・・。(まぁとりあえず今は正しく動いていることが確認できただけでヨシとします。)
上記コードですが
FMT_P0 = FMTClass(MODP=469762049 , MODP_Wn=CreateWn(60733,469762049,26))
このインスタンスに初期値を設定するところで、CreateWn関数を使っています。ここで要素数$2^N$に応じた原始$2^N$乗根を生成している感じです。例えば$60733$は$1$の$2^{26}$乗根と分かっているので、$2^{25}$乗根は$60733*60733$ $(mod$ $469762049)$で簡単に計算できます。
また余談ですが、自前で$P$とそれに対応する原始$2^N$乗根を探しあてるには全探索しても良いのですが、フェルマーの小定理を知っておくと良いかもしれません。今回使っているPはそれぞれ
$2013265921=15×2^{27}+1$
$1811939329=27×2^{26}+1$
$469762049 = 7×2^{26}+1$
であり、それぞれ$2^{27}$乗根、$2^{26}$乗根、$2^{26}$乗根まで存在します。
私は$2^N$に適当な数をかけて1を足した数が素数かどうかを判定して、素数ならあとは全探索で$2^{N}$乗根を探す、といった感じでやりました。
さらに余談ですが、使うPは素数である必要はなく、Garnerで復元できる条件を満たすかつdigitNと互いに素であればなんでも良いです(多分)。
フェルマー小定理の参考
https://qiita.com/drken/items/6b4031ccbb2cab7436f3
3-3 負巡回畳み込みを使って0埋め領域を活用
ここまで触れて来ませんでしたが
A=np.uint32([1,4,1,4,0,0,0,0])
B=np.uint32([2,1,3,5,0,0,0,0])
の右半分の0は有効活用できないでしょうか。結論から言うとできます。ここを0以外にすると、結果の上位桁が一周回って下位桁に加算されます。
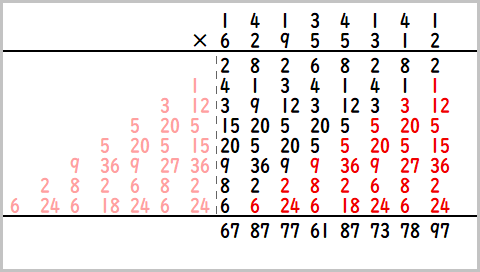
見てみたほうが早いので最初のfmt_smaple0.pyで以下の初期値にして試してみます。
A=np.uint32([1,4,1,4,3,1,4,1])
B=np.uint32([2,1,3,5,5,9,2,6])
結果
畳み込みの結果
C[ 0 ] = 97
C[ 1 ] = 78
C[ 2 ] = 73
C[ 3 ] = 87
C[ 4 ] = 61
C[ 5 ] = 77
C[ 6 ] = 87
C[ 7 ] = 67
薄いピンクのところが1周回って畳み込まれています。これが正巡回畳み込みです。
次にピンクの上位桁の復元をみすえて負巡回畳み込みというのをします。同じA,Bを使ってFMTに使う$ω^{nk}$を$ω^{n(k+1/2)}$に変更します。すると
畳み込みの結果
C[ 0 ] = 164
C[ 1 ] = 197
C[ 2 ] = 202
C[ 3 ] = 222
C[ 4 ] = 15
C[ 5 ] = 25
C[ 6 ] = 75
C[ 7 ] = 67
 こうなります。(画像とプログラムの出力は257剰余下でどちらも同じ値です。)
こうなります。(画像とプログラムの出力は257剰余下でどちらも同じ値です。)
この正巡回と負巡回の結果を使えば
(正巡回-負巡回)/2 で上位桁
(正巡回+負巡回)/2 で下位桁
を復元できます。もちろん小数はありえない世界なので剰余下でやります。
少し戻って、さっきの$ω^{n(k+1/2)}$にするというところについてもう少し詳しく解説します。そもそも元のFMT関数はaを入力としてこのようなfを出力していました。
$f_k=a_0ω^{0}+a_1ω^{k}+a_2ω^{2k}....+a_{n-1}ω^{(n-1)k}$
負巡回ではこれをこうします。
$f_k=a_0ω^{0}+a_1ω^{k+(1/2)}+a_2ω^{2(k+(1/2))}....+a_{n-1}ω^{(n-1)(k+(1/2))}$
以下がこれをコードに書き起こしたものになります。
$ω=4$、法$P=257$として
# digitN=8
# MODP=257
# FMT関数と同じ。ナイーブO(N^2)実装
def naiveFMT(inputA):
arrayA=np.zeros_like(inputA)
for i in range(digitN):
for j in range(digitN):
arrayA[i]+=inputA[j]*ModExp(4,i*j)
arrayA[i]%=MODP
return arrayA[:]
# 負巡回FMT
def naiveFMT_Neg(inputA):
arrayA = np.zeros_like(inputA)
for i in range(digitN):
for j in range(digitN):
arrayA[i]+=inputA[j]*ModExp(2,(i*2+1)*j)
arrayA[i]%=MODP
return arrayA[:]
こうなります。このやり方は$O(N^2)$の形ですが、実際の実装ではFMT関数部分を変えず、順変換の前にA[i],B[i]に$ω^{i/2}$をかけ、逆変換の後に$ω^{-i/2}$をかける処理を追加すれば良いです。この追加処理自体は線形時間なので負巡回の計算オーダーは正巡回と同じと言えます。
また今回は偶然$ω$の2乗根が存在したので大丈夫でしたが、$ω$の2乗根が存在しない場合は$ω^{1/2}$が計算できないので負巡回ができません。そのためにも原始$2^N$乗根の$2^N$がなるべく大きくなるものを探しておきたいものです。
負巡回畳み込みについて参考にさせて頂きました。
【FFTでの正巡回、負巡回畳み込みの話】
https://qiita.com/peria/items/cf4c4b72ebbeec7728af#fnref1
【FMT先駆者様のスライド】
http://ushiro.jp/research/fmt/sld021.htm
3-4 時間間引きFMTと周波数間引きFMTでビット逆順を相殺
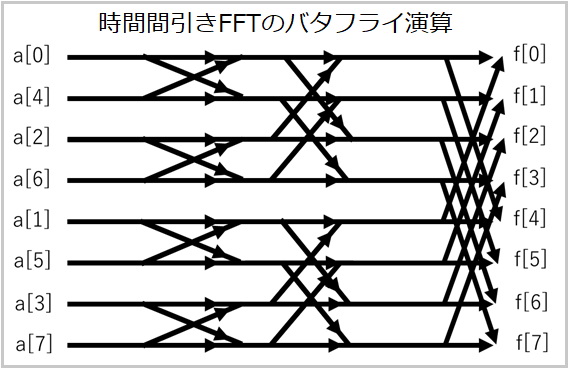
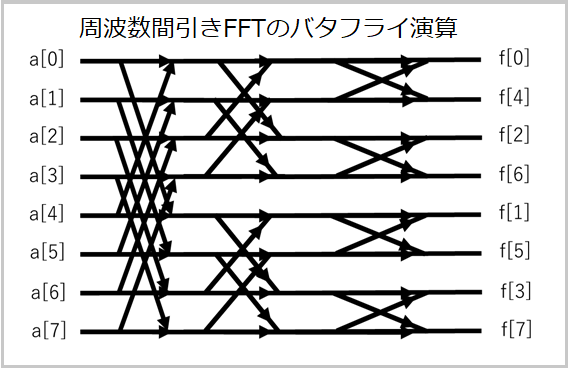
時間間引きFMTとか周波数間引きFMTという言葉はありませんが、時間間引きFFTと周波数間引きFFTのFMT版ということです。FFTでもFMTでもバタフライ演算の前か後ろに配列ビット逆順の処理が必要です。
稚拙なイメージ画像で申し訳ないですが、言いたいこととしては時間間引きFFTはバタフライ演算の前に配列ビット逆順が必要、周波数間引きFFTはバタフライ演算の後に配列ビット逆順が必要ということです。
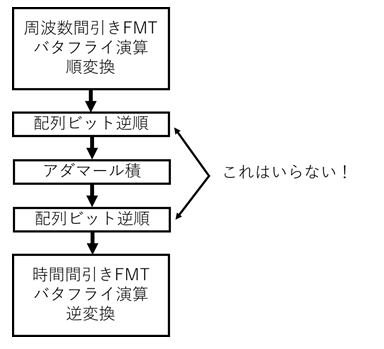
上記ソースコードではFMT関数は時間間引きFFTを参考に書いてるので、バタフライ演算の前にビット逆順が必要になっています。逆変換も時間間引きです。ということは、順変換を周波数間引きにして、逆変換を時間間引きにすればビット逆順が相殺されます!途中にあるA[i]*B[i]のアダマール積は配列の順番関係ないので気にしなくていいです。
FMT:時間間引き順変換
iFMT:時間間引き逆変換
uFMT:周波数間引き順変換
iuFMT:周波数間引き逆変換
とし、負巡回も込みで実装すると
import numpy as np
# aの逆元を返す mod m
def modinv(a,m):
b = m
u = 1
v = 0
while (b) :
t = a // b
a -= t * b
tmp=a
a=b
b=tmp
u -= t * v
tmp = u
u = v
v = tmp
u %= m
if u < 0:
u += m
return u
# garnerのアルゴリズム、3変数ver
# 64bit整数におさまらない可能性あり、pythonのint型を使用
def Garner(a_,b_,c_,ar_,br_,cr_):
a = int(a_)
b = int(b_)
c = int(c_)
ar = int(ar_)
br = int(br_)
cr = int(cr_)
x = ar + (br - ar) * modinv(a,b) % b * a
x = x + (cr - x % c) * modinv(a,c) % c * modinv(b,c) % c * a * b
#x %= a*b*c #a<b<cのときこの処理は必要ない
return x
class FMTClass():
def __init__(self,MODP,MODP_WnSqrt):
self.MODP=np.uint32(MODP)
self.MODP_WnSqrt = np.uint32(MODP_WnSqrt)
self.MODP_Wn = np.uint32(np.uint64(self.MODP_WnSqrt) * np.uint64(self.MODP_WnSqrt) % np.uint64(self.MODP))
# MODP剰余下でaのb乗を返す
# 追記1:np.uint32(pow(np.uint32(a),np.uint32(b),np.uint32(self.MODP)))を使ったほうが速い!
def ModExp(self,a, b):
ans = np.uint64(1)
aa = np.uint64(a)
while (b != 0):
if (b % 2 == 1):
ans = ans * aa % np.uint64(self.MODP)
aa = aa * aa % np.uint64(self.MODP)
b //= 2
return np.uint32(ans)
def FMT(self,inputA):
arrayA=inputA.copy()
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = self.ModExp(self.MODP_Wn, t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(self.MODP))
arrayA[t1] = (arrayAt0 + self.MODP - w1) % self.MODP
arrayA[t0] = (arrayAt0 + w1) % self.MODP
return arrayA[:]
def iFMT(self,inputA):
arrayA = inputA.copy()
for i in range(digit_level):
loopCnt_Pow2 = 1 << i
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = self.ModExp(self.MODP_Wn, digitN - t2 * (1 << (digit_level - 1 - i)))
w1 = np.uint32(np.uint64(arrayAt1) * np.uint64(w0) % np.uint64(self.MODP))
arrayA[t1] = (arrayAt0 + self.MODP - w1) % self.MODP
arrayA[t0] = (arrayAt0 + w1) % self.MODP
return arrayA[:]
def uFMT(self,inputA):
arrayA = inputA.copy()
for i in range(digit_level):
loopCnt_Pow2 = 1 << (digit_level - i - 1)
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = self.ModExp(self.MODP_Wn, t2 * (1 << i))
r0 = (arrayAt0 - arrayAt1 + self.MODP) % self.MODP
r1 = (arrayAt0 + arrayAt1) % self.MODP
w1 = np.uint32(np.uint64(r0) * np.uint64(w0) % np.uint64(self.MODP))
arrayA[t1] = w1
arrayA[t0] = r1
return arrayA[:]
def iuFMT(self,inputA):
arrayA = inputA.copy()
for i in range(digit_level):
loopCnt_Pow2 = 1 << (digit_level - i - 1)
for idx in range(digitN // 2):
t2 = idx % loopCnt_Pow2
t0 = idx * 2 - t2
t1 = t0 + loopCnt_Pow2
arrayAt0 = arrayA[t0]
arrayAt1 = arrayA[t1]
w0 = self.ModExp(self.MODP_Wn, digitN - t2 * (1 << i))
r0 = (arrayAt0 - arrayAt1 + self.MODP) % self.MODP
r1 = (arrayAt0 + arrayAt1) % self.MODP
w1 = np.uint32(np.uint64(r0) * np.uint64(w0) % np.uint64(self.MODP))
arrayA[t1] = w1
arrayA[t0] = r1
return arrayA[:]
def DivN(self,inputA):
digitN_r = modinv(digitN, int(self.MODP)) # digitNの逆元を計算
ret = np.uint64(inputA[:]) * np.uint64(digitN_r) % np.uint64(self.MODP)
return np.uint32(ret)
def PreNegFMT(self,A):
for i in range(digitN):
A[i] = np.uint32(np.uint64(A[i]) * np.uint64(self.ModExp(self.MODP_WnSqrt, i)) % np.uint64(self.MODP))
return A[:]
def PostNegFMT(self,A):
for i in range(digitN):
A[i] = np.uint32(
np.uint64(A[i]) * np.uint64(self.ModExp(self.MODP_WnSqrt, digitN * 2 - i)) % np.uint64(self.MODP))
return A[:]
#A*Bの畳み込み結果を返す
#上位桁、下位桁を復元して2倍の要素数で返す
def Convolution(self,A_,B_):
#正巡回
A = self.uFMT(A_%self.MODP)
B = self.uFMT(B_%self.MODP)
Cpos = np.uint64(A[:]) * np.uint64(B[:]) % np.uint64(self.MODP) # 各要素どうし乗算
Cpos = np.uint32(Cpos) #結果は32bit範囲内におさまってるので
Cpos = self.iFMT(Cpos) # 逆変換
Cpos = self.DivN(Cpos) # Nで割る
# 負巡回
A = self.PreNegFMT(A_ % self.MODP)#負巡回の前処理
B = self.PreNegFMT(B_ % self.MODP)#負巡回の前処理
A = self.uFMT(A)
B = self.uFMT(B)
Cneg = np.uint64(A[:]) * np.uint64(B[:]) % np.uint64(self.MODP) # 各要素どうし乗算
Cneg = np.uint32(Cneg) # 結果は32bit範囲内におさまってるので
Cneg = self.iFMT(Cneg) # 逆変換
Cneg = self.DivN(Cneg) # Nで割る
Cneg = self.PostNegFMT(Cneg) # 負巡回の後処理
#上位桁、下位桁 復元
Elo = (Cpos + Cneg) % self.MODP
Elo = (Elo + Elo % 2 * self.MODP) // 2
Ehi = (Cpos - Cneg + self.MODP) % self.MODP
Ehi = (Ehi + Ehi % 2 * self.MODP) // 2
E = np.zeros(digitN*2).astype(np.uint32)
E[:digitN] = Elo[:]
E[digitN:] = Ehi[:]
return E[:]
# 検算用。A,Bの配列から一つの多倍長整数を作る。pythonのint型は乗算にKaratsuba法を使っているのでちょっと速い
def CalcAB(A,B):
Alist = A.tolist()
Blist = B.tolist()
r=2**32
for i in range(digit_level):
for j in range(2**(digit_level-1-i)):
Alist[j] = Alist[j * 2] + Alist[j * 2 + 1] * r
Blist[j] = Blist[j * 2] + Blist[j * 2 + 1] * r
r = r * r
return Alist[0] * Blist[0]
# 検算用。Eから一つの多倍長整数を作る
def CalcE(E):
Elist = E.tolist()
r = 2 ** 32
for i in range(digit_level + 1):
for j in range(2 ** (digit_level - i)):
Elist[j] = Elist[j * 2] + Elist[j * 2 + 1] * r
r = r * r
return Elist[0]
def CreateWnSqrt(a,m,n_level):
ans=a
for i in range(n_level-digit_level-1):#負巡回で使うことを考え-1
ans=ans*ans%m
return ans
# E0,E1,E2を使ってgarnerでEを復元して繰り上がり処理
def Carrying(E0,E1,E2):
E = np.zeros(digitN * 2).astype(np.uint32)
upg = 0 # 繰り上がり分 python3のint型なのでオーバーフローの心配はない
for i in range(digitN * 2):
g = Garner(FMT_P0.MODP, FMT_P1.MODP, FMT_P2.MODP, E0[i], E1[i], E2[i])
g += upg
E[i] = np.uint32(g % 4294967296)
upg = g//4294967296
return E
if __name__=="__main__":
digit_level = 16
digitN = 1 << digit_level
FMT_P0 = FMTClass(MODP=469762049 , MODP_WnSqrt=CreateWnSqrt(60733,469762049,26))
FMT_P1 = FMTClass(MODP=1811939329, MODP_WnSqrt=CreateWnSqrt(59189,1811939329,26))
FMT_P2 = FMTClass(MODP=2013265921, MODP_WnSqrt=CreateWnSqrt(52278,2013265921,27))
# A,Bの初期化。前半後半ともにランダムな値をいれる。
A_ = np.zeros(digitN).astype(np.uint32)
A_[:] = np.uint32( np.random.randint(0, 2147483648, (digitN)) * 2
+ np.random.randint(0, 2, (digitN)))
B_ = np.zeros(digitN).astype(np.uint32)
B_[:] = np.uint32(np.random.randint(0, 2147483648, (digitN)) * 2
+ np.random.randint(0, 2, (digitN)))
#p=469762049でやる
E0 = FMT_P0.Convolution(A_,B_)
#p=1811939329でやる
E1 = FMT_P1.Convolution(A_, B_)
#p=2013265921でやる
E2 = FMT_P2.Convolution(A_, B_)
#結果一部表示表示
print("畳み込みの結果 mod","469762049",
"\t\t畳み込みの結果 mod","1811939329",
"\t\t畳み込みの結果 mod", "2013265921",
"\t\tGarnerで復元")
for i in range(10):
print("E[",i,"] =",E0[i],
" \t\t\t\t", "E[", i, "] =", E1[i],
" \t\t\t\t", "E[", i, "] =", E2[i],
"\t\t\t\t",Garner(FMT_P0.MODP,FMT_P1.MODP,FMT_P2.MODP,E0[i],E1[i],E2[i])
)
#繰り上がり
E=Carrying(E0,E1,E2)
#検算
print("検算開始")
if CalcAB(A_, B_)==CalcE(E):
print("正解!")
else:
print("ちがう!")
これでビット逆順の計算をなくし、A,Bの0埋め領域も消すことができました。また「FMT」関数と「iuFMT」関数は書いてはありますが実際には使われていません。
4 CUDAに移植
以上のコードをCUDAに移植します。私はPythonからCUDAをいじることが多いのでここではPyCUDAを使わせてください。
実行環境
GPU:RTX2080Ti
OS:Windows 10
Cuda compilation tools, release 10.1, V10.1.168
python 3.7.1 (Anaconda)
pyCUDA 2019.1 (CUDA 10.1に対応,pipコマンドでinstall)
(長いので折りたたんでいます。)
fmt_smaple5.py
# FMT(高速剰余変換) PyCUDA版
# 3つの素数PのもとでFMTを行うサンプル
# garnerのアルゴリズムで最後に値を復元しているため、2の90.7乗まで正確に復元できる
# 検算関数もあり
# 追記1:これより1.2~1.8倍速いバージョンあり。(githubにある。剰余をモンゴメリ乗算に変えたやつ)
# 追記2:これより2~5倍速いバージョンあり。剰余をあらかじめ計算して参照するタイプ(sample6)
import pycuda.autoinit
import pycuda.driver as drv
from pycuda.compiler import SourceModule
import numpy as np
import time
import os
programid_garner=SourceModule("""
#include "garner.cu"
""",include_dirs=[os.getcwd()])
kernel_garner=programid_garner.get_function("GarnerGPU")
class FMTClass():
def __init__(self,MODP,MODP_WnSqrt):
self.MODP=np.uint32(MODP)
self.MODP_WnSqrt = np.uint32(MODP_WnSqrt)
self.MODP_Wn = np.uint32(np.uint64(self.MODP_WnSqrt) * np.uint64(self.MODP_WnSqrt) % np.uint64(self.MODP))
self.programid = SourceModule("""
#define MODP (uint)(""" + str(MODP) + """)
#include "fmt.cu"
""", include_dirs=[os.getcwd()])
self.kernel_FMT=self.programid.get_function("FMT")
self.kernel_iFMT=self.programid.get_function("iFMT")
self.kernel_uFMT=self.programid.get_function("uFMT")
self.kernel_iuFMT=self.programid.get_function("iuFMT")
self.kernel_Mul_i_i=self.programid.get_function("Mul_i_i")
self.kernel_PostNegFMT=self.programid.get_function("PostNegFMT")
self.kernel_PreNegFMT=self.programid.get_function("PreNegFMT")
self.kernel_DivN=self.programid.get_function("DivN")
self.kernel_PosNeg_To_HiLo=self.programid.get_function("PosNeg_To_HiLo")
self.kernel_PostFMT_DivN_HiLo=self.programid.get_function("PostFMT_DivN_HiLo")
def FMT(self,gpuMemA):
for i in range(digit_level):
self.kernel_FMT(gpuMemA, np.uint32(1 << i), self.MODP_Wn, np.uint32(1 << (digit_level - 1)),
grid=(gsz // lsz, 1, 1), block=(lsz, 1, 1))
return
def uFMT(self,gpuMemA):
for i in range(digit_level):
self.kernel_uFMT(gpuMemA, np.uint32((1<<(digit_level-1))>>i), self.MODP_Wn, np.uint32(1 << (digit_level - 1)),
grid=(gsz // lsz, 1, 1), block=(lsz, 1, 1))
return
def iFMT(self,gpuMemA):
for i in range(digit_level):
self.kernel_iFMT(gpuMemA, np.uint32(1 << i), self.MODP_Wn,
np.uint32(1 << (digit_level - 1)), grid=(gsz // lsz, 1, 1), block=(lsz, 1, 1))
return
def iuFMT(self,gpuMemA):
for i in range(digit_level):
self.kernel_iuFMT(gpuMemA, np.uint32(1<<(digit_level-1-i)), self.MODP_Wn,
np.uint32(1 << (digit_level - 1)), grid=(gsz // lsz, 1, 1), block=(lsz, 1, 1))
return
def Mul_i_i(self,gpuMemA,gpuMemB):
self.kernel_Mul_i_i(gpuMemA, gpuMemB, grid=(gsz2 // lsz2, 1, 1), block=(lsz2, 1, 1))
return
def DivN(self,gpuMemA):
self.kernel_DivN(gpuMemA, np.uint32(1<<digit_level), grid=(gsz2 // lsz2, 1, 1), block=(lsz2, 1, 1))
return
def PreNegFMT(self,gpuMemA,gpuMemB):
self.kernel_PreNegFMT(gpuMemA,gpuMemB, self.MODP_WnSqrt,
np.uint32(1<<digit_level), grid=(gsz2 // lsz2, 1, 1), block=(lsz2, 1, 1))
return
def PostNegFMT(self,gpuMemA):
self.kernel_PostNegFMT(gpuMemA, self.MODP_WnSqrt,
np.uint32(1<<digit_level), grid=(gsz2 // lsz2, 1, 1), block=(lsz2, 1, 1))
return
def PosNeg_To_HiLo(self,gpuMemE,gpuMemA,gpuMemB):
self.kernel_PosNeg_To_HiLo(gpuMemE, gpuMemA,gpuMemB, np.uint32(1 << digit_level),
grid=(gsz2 // lsz2, 1, 1), block=(lsz2, 1, 1))
return
def PostFMT_DivN_HiLo(self,gpuMemE,gpuMemA,gpuMemB):
self.kernel_PostFMT_DivN_HiLo(gpuMemE, gpuMemA, gpuMemB, np.uint32(1 << digit_level),
self.MODP_WnSqrt,grid=(gsz2 // lsz2, 1, 1), block=(lsz2, 1, 1))
return
# FMTで畳み込み乗算の結果を得る
# A,Bは計算過程で内部が破壊されているので注意
def Convolution(self,A,B):
A_Neg = drv.mem_alloc(4 * digitN) #4=sizeof(uint)
B_Neg = drv.mem_alloc(4 * digitN) # 4=sizeof(uint)
E = drv.mem_alloc(4 * digitN * 2) # 4=sizeof(uint)
self.PreNegFMT(A,A_Neg)#負順回用
self.PreNegFMT(B,B_Neg)#負順回用
self.uFMT(A)
self.uFMT(B)
self.uFMT(A_Neg)
self.uFMT(B_Neg)
self.Mul_i_i(A,B)#Bに結果が入る
self.Mul_i_i(A_Neg,B_Neg)#Bに結果が入る
self.iFMT(B)
self.iFMT(B_Neg)
self.PostNegFMT(B_Neg)
self.DivN(B)#FFTみたくNで最後割らないといけない
self.DivN(B_Neg)
self.PosNeg_To_HiLo(E,B,B_Neg)#eに結果が入る
#PostFMT_DivN_HiLo(E,B,B_Neg) # 上4行のかわりにこれをつかってもよい
drv.DeviceAllocation.free(A_Neg)
drv.DeviceAllocation.free(B_Neg)
return E
def Creategszlsz():
gsz = 1 << (digit_level - 1) # gpu global_work_size
lsz = min(gsz, 256) # gpu local_work_size
gsz2 = digitN
lsz2 = min(gsz2, 256)
return gsz, lsz, gsz2, lsz2
# 検算用。A,Bの配列から一つの多倍長整数を作る。pythonのint型は乗算にKaratsuba法を使っているのでちょっと速い
def CalcAB(A,B):
Alist = A.tolist()
Blist = B.tolist()
r=2**32
for i in range(digit_level):
for j in range(2**(digit_level-1-i)):
Alist[j] = Alist[j * 2] + Alist[j * 2 + 1] * r
Blist[j] = Blist[j * 2] + Blist[j * 2 + 1] * r
r = r * r
return Alist[0] * Blist[0]
# 検算用。Eから一つの多倍長整数を作る
def CalcE(E):
Elist = E.tolist()
r = 2 ** 32
for i in range(digit_level + 1):
for j in range(2 ** (digit_level - i)):
Elist[j] = Elist[j * 2] + Elist[j * 2 + 1] * r
r = r * r
return Elist[0]
# 検算
def AnswerCheck(host_A,host_B,host_E):
print("検算開始")
CPUres = CalcAB(host_A, host_B)
GPUres = CalcE(host_E)
if CPUres!=GPUres:
print("not equal !!!!!!!")
print(CPUres)
print(GPUres)
else:
print("あってる")
return
def InitializeAB():
host_A = np.random.randint(2107483648, size=(digitN)).astype(np.uint32) * 2\
+ np.random.randint(2, size=(digitN)).astype(np.uint32)
host_B = np.random.randint(2107483648, size=(digitN)).astype(np.uint32) * 2\
+ np.random.randint(2, size=(digitN)).astype(np.uint32)
return host_A,host_B
def CreateWnSqrt(a,m,n_level):
ans=a
for i in range(n_level-digit_level-1):#負巡回で使うことを考え-1
ans=ans*ans%m
return ans
# E0,E1,E2を使ってgarnerでEを復元して繰り上がり処理。結果はGPU内
def Carrying(E0,E1,E2,E):
gsz3 = 1 << (digit_level+1)
lsz3 = min(gsz3, 256)
kernel_garner(E0,E1,E2,E,np.uint32(digitN*2),
grid=(gsz3 // lsz3, 1, 1),block=(lsz3, 1, 1))
return
if __name__ == '__main__':
digit_level = 25 #################################可変パラメーター############################# 最大25
digitN = 1 << digit_level
gsz, lsz, gsz2, lsz2 = Creategszlsz()#GPUカーネルのgridサイズblockサイズ計算
print("A,Bの要素数=",digitN)
FMT_P0 = FMTClass(MODP=469762049 , MODP_WnSqrt=CreateWnSqrt(60733,469762049,26))
FMT_P1 = FMTClass(MODP=1811939329, MODP_WnSqrt=CreateWnSqrt(59189,1811939329,26))
FMT_P2 = FMTClass(MODP=2013265921, MODP_WnSqrt=CreateWnSqrt(52278,2013265921,27))
host_E = np.zeros(digitN * 2).astype(np.uint32)#結果格納用
E = drv.to_device(host_E) # gpuメモリ確保。かならず0に初期化しておかないといけない
print("初期値生成")
host_A, host_B = InitializeAB()
A0 = drv.to_device(host_A) # gpuメモリ確保&転送
B0 = drv.to_device(host_B) # gpuメモリ確保&転送
A1 = drv.to_device(host_A) # gpuメモリ確保&転送
B1 = drv.to_device(host_B) # gpuメモリ確保&転送
A2 = drv.to_device(host_A) # gpuメモリ確保&転送
B2 = drv.to_device(host_B) # gpuメモリ確保&転送
print("GPU計算開始")
stime = time.time()
E0 = FMT_P0.Convolution(A0, B0)
E1 = FMT_P1.Convolution(A1, B1)
E2 = FMT_P2.Convolution(A2, B2)
# ここからgarner&繰り上がり、E0,E1,E2から復元繰り上げしEに出力
Carrying(E0, E1, E2 , E)
drv.Context.synchronize() #タスク待ち命令
print("GPU計算終了",time.time()-stime,"sec")
# 結果をGPU→CPU
drv.memcpy_dtoh(host_E, E)
# 検算 ここは桁数が多いととても重い。digit_level = 20で約30秒
#AnswerCheck(host_A, host_B, host_E)
fmt.cu
# define ulong unsigned long long
# define uint unsigned int
//A*B%MODP
__device__ uint ABModC(uint a,uint b){
ulong tmp=((ulong)(__umulhi(a,b)))*(1ULL<<32)+(ulong)(a*b);
return (uint)(tmp%MODP);
}
//exp(a,b)%MODP
__device__ uint ModExp(uint a,uint b){
ulong ans=1ULL;
ulong aa=a;
while(b!=0){
if (b%2==1) ans=ans*aa%MODP;
aa=aa*aa%MODP;
b/=2;
}
return (uint)ans;
}
//逆変換後は、FFTでいうNで除算しないといけない。
// a/arrayLength mod P
__device__ uint DivN_f(uint a,uint arrayLength)
{
uint as =a/arrayLength;
uint ar =a-as*arrayLength;
uint pn =MODP/arrayLength;
if (ar!=0){
as+=(arrayLength-ar)*pn+1;
}
return as;
}
//arrayLength2 = arrayLength/2
__global__ void FMT(uint *arrayA,uint loopCnt_Pow2,uint omega,uint arrayLength2 ) {
uint idx = threadIdx.x+blockIdx.x*256;
uint t2 = idx%loopCnt_Pow2;
uint t0 = idx*2-t2;
uint t1 = t0+loopCnt_Pow2;
uint w0;
uint w1;
uint arrayAt0=arrayA[t0];
uint arrayAt1=arrayA[t1];
uint r0;
uint r1;
w0=ModExp(omega,t2*(arrayLength2/loopCnt_Pow2));
w1=ABModC(arrayAt1,w0);
r0=arrayAt0-w1+MODP;
r1=arrayAt0+w1;
if (r0>=MODP){r0-=MODP;}
if (r1>=MODP){r1-=MODP;}
arrayA[t1]=r0;
arrayA[t0]=r1;
}
__global__ void uFMT(uint *arrayA,uint loopCnt_Pow2,uint omega,uint arrayLength2 ) {
uint idx = threadIdx.x+blockIdx.x*256;
uint t2 = idx%loopCnt_Pow2;
uint t0 = idx*2-t2;
uint t1 = t0+loopCnt_Pow2;
uint w0;
uint w1;
uint arrayAt0=arrayA[t0];
uint arrayAt1=arrayA[t1];
uint r0;
uint r1;
w0=ModExp(omega,t2*(arrayLength2/loopCnt_Pow2));
r0=arrayAt0-arrayAt1+MODP;
r1=arrayAt0+arrayAt1;
if (r0>=MODP){r0-=MODP;}
if (r1>=MODP){r1-=MODP;}
w1=ABModC(r0,w0);
arrayA[t1]=w1;
arrayA[t0]=r1;
}
__global__ void iFMT(uint *arrayA,uint loopCnt_Pow2,uint omega,uint arrayLength2 ) {
uint idx = threadIdx.x+blockIdx.x*256;
uint t2 = idx%loopCnt_Pow2;
uint t0 = idx*2-t2;
uint t1 = t0+loopCnt_Pow2;
uint w0;
uint w1;
uint arrayAt0=arrayA[t0];
uint arrayAt1=arrayA[t1];
uint r0;
uint r1;
w0=ModExp(omega,arrayLength2*2-t2*(arrayLength2/loopCnt_Pow2));
w1=ABModC(arrayAt1,w0);
r0=arrayAt0-w1+MODP;
r1=arrayAt0+w1;
if (r0>=MODP){r0-=MODP;}
if (r1>=MODP){r1-=MODP;}
arrayA[t1]=r0;
arrayA[t0]=r1;
}
__global__ void iuFMT(uint *arrayA,uint loopCnt_Pow2,uint omega,uint arrayLength2 ) {
uint idx = threadIdx.x+blockIdx.x*256;
uint t2 = idx%loopCnt_Pow2;
uint t0 = idx*2-t2;
uint t1 = t0+loopCnt_Pow2;
uint w0;
uint w1;
uint arrayAt0=arrayA[t0];
uint arrayAt1=arrayA[t1];
uint r0;
uint r1;
w0=ModExp(omega,arrayLength2*2-t2*(arrayLength2/loopCnt_Pow2));
r0=arrayAt0-arrayAt1+MODP;
r1=arrayAt0+arrayAt1;
if (r0>=MODP){r0-=MODP;}
if (r1>=MODP){r1-=MODP;}
w1=ABModC(r0,w0);
arrayA[t1]=w1;
arrayA[t0]=r1;
}
//同じ要素同士の掛け算
__global__ void Mul_i_i(uint *arrayA,uint *arrayB ) {
uint idx = threadIdx.x+blockIdx.x*256;
uint w0;
w0=ABModC(arrayB[idx],arrayA[idx]);
arrayB[idx]=w0;
}
//逆変換後のNで割るやつ。剰余下で割るには特殊処理が必要
__global__ void DivN(uint *arrayA,uint arrayLength ) {
uint idx = threadIdx.x+blockIdx.x*256;
arrayA[idx]=DivN_f(arrayA[idx],arrayLength);
}
//負巡回計算の前処理
//sqrt_omegaの2N乗が1 (mod P)
//a[0]*=ModExp(sqrt_omega,0)
//a[1]*=ModExp(sqrt_omega,1)
//a[2]*=ModExp(sqrt_omega,2)
//a[3]*=ModExp(sqrt_omega,3)
__global__ void PreNegFMT(uint *arrayA,uint *arrayB,uint sqrt_omega,uint arrayLength) {
uint idx = threadIdx.x+blockIdx.x*256;
arrayA[idx]%=MODP;
uint w0=ModExp(sqrt_omega,idx);
arrayB[idx]=ABModC(arrayA[idx],w0);
}
//負巡回計算の後処理
//sqrt_omegaの2N乗が1 (mod P)
//a[0]*=ModExp(sqrt_omega,-0)
//a[1]*=ModExp(sqrt_omega,-1)
//a[2]*=ModExp(sqrt_omega,-2)
//a[3]*=ModExp(sqrt_omega,-3)
__global__ void PostNegFMT(uint *arrayA,uint sqrt_omega,uint arrayLength) {
uint idx = threadIdx.x+blockIdx.x*256;
uint w0=ModExp(sqrt_omega,arrayLength*2-idx);
arrayA[idx]=ABModC(arrayA[idx],w0);
}
//負巡回計算と正巡回計算結果から、上半分桁と下半分桁を求める
__global__ void PosNeg_To_HiLo(uint *arrayE,uint *arrayA,uint *arrayB,uint arrayLength) {
uint idx = threadIdx.x+blockIdx.x*256;
uint a=arrayA[idx];
uint b=arrayB[idx];
uint subab=(a-b+MODP);//まず(a-b)/2を求めたい
uint flag=subab%2;
subab-=MODP*((subab>=MODP)*2-1)*flag;//ここで絶対偶数になる
subab/=2;//(a-b)/2 MOD Pを算出
arrayE[idx+arrayLength]=subab;//上位桁は(a-b)/2 MOD P
arrayE[idx]=a-subab+MODP*(a<subab);//a-((a-b)/2)=a/2+b/2 つまり(a+b)/2が下位桁
}
//vramへの書き込み回数を減らす目的に作った関数
//PostNegFMT関数とDivN関数とPosNeg_To_HiLo関数の統合版
__global__ void PostFMT_DivN_HiLo(uint *arrayE,uint *arrayA,uint *arrayB,uint arrayLength,uint sqrt_omega) {
uint idx = threadIdx.x+blockIdx.x*256;
uint a=arrayA[idx];
uint b=arrayB[idx];
//ここは負巡回の後処理計算部分
uint w0=ModExp(sqrt_omega,idx+(idx%2)*arrayLength);
b=ABModC(b,w0);
//Nで除算する関数
a=DivN_f(a,arrayLength);
b=DivN_f(b,arrayLength);
//あとは一緒
uint subab=(a-b+MODP);//まず(a-b)/2を求めたい
uint flag=subab%2;
subab-=MODP*((subab>=MODP)*2-1)*flag;//ここで絶対偶数になる
subab/=2;//(a-b)/2 MOD Pを算出
arrayE[idx+arrayLength]=subab;//上位桁は(a-b)/2 MOD P
arrayE[idx]=a-subab+MODP*(a<subab);//a-((a-b)/2)=a/2+b/2 つまり(a+b)/2が下位桁
}
garner.cu
# define ulong unsigned long long
# define uint unsigned int
# define MOD_P0 469762049LL
# define MOD_P1 1811939329LL
# define MOD_P2 2013265921LL
//3つの互いに素なPが与えられるので、それぞれの余りから元の値を復元したい
//このときPは全て固定なので剰余計算は全部決め打ちでいける
//E0~E2が入力、E3に出力
//繰り上がりも考慮
//arrayLength2=arrayE3の配列サイズ
__global__ void GarnerGPU(uint *arrayE0,uint *arrayE1,uint *arrayE2,uint *arrayE3,uint arrayLength2 ) {
int idx = threadIdx.x+blockIdx.x*256;
ulong ar=arrayE0[idx];
ulong br=arrayE1[idx];
ulong cr=arrayE2[idx];
ulong x=ar;
ulong brx=br-x+MOD_P1;
if (brx>=MOD_P1)brx-=MOD_P1;
x=x+(brx*1540148431)%MOD_P1*MOD_P0;
//1540148431=modinv(MOD_P0,MOD_P1)
//この時点でxはMOD_P1*MOD_P0以下であることが保証されている
ulong crx=cr+MOD_P2-x%MOD_P2;
if (crx>=MOD_P2)crx-=MOD_P2;
ulong w1=(crx*1050399624)%MOD_P2;
//1050399624=modinv(MOD_P0,MOD_P2) *modinv(MOD_P1,MOD_P2)%MOD_P2
ulong w2=MOD_P0*MOD_P1;
ulong out_lo=w1*w2;
ulong out_hi=__umul64hi(w1,w2);
if (out_lo>(out_lo+x)){
out_hi++;
}
out_lo+=x;
//ここから繰り上がり処理
uint ui00_32=(uint)(out_lo%(1ULL<<32ULL));
uint ui32_64=(uint)(out_lo/(1ULL<<32ULL));
uint ui64_96=(uint)(out_hi%(1ULL<<32ULL));
uint lastE3_0 = atomicAdd( &arrayE3[idx+0], ui00_32 );
if ((lastE3_0+ui00_32)<lastE3_0){//繰り上がりを考慮
ui32_64++;
if (ui32_64==0)ui64_96++;
}
if (ui32_64!=0){
uint lastE3_1 = atomicAdd( &arrayE3[idx+1], ui32_64 );
if ((lastE3_1+ui32_64)<lastE3_1){//繰り上がりを考慮
ui64_96++;//こいつがオーバーフローすることは絶対にない
}
}
uint upflg=0;
if (ui64_96!=0){
uint lastE3_2 = atomicAdd( &arrayE3[idx+2], ui64_96 );
if ((lastE3_2+ui64_96)<lastE3_2){//繰り上がりを考慮
upflg++;
}
}
uint lastE3_i;
for(int i=idx+3;i<arrayLength2;i++){ //9999999+1みたいなとき用
if (upflg==0)break;
lastE3_i = atomicAdd( &arrayE3[i], upflg );
if (lastE3_i==4294967295){
upflg=1;
}else{
upflg=0;
}
}
}
3つのファイルは同じディレクトリに入れていれば動くはずです。
さてCUDAに移植する際にそのままは移植できないのでいくつか工夫する必要がありました。Garnerで復元するところはlong型を超える値が出てきてしまい(だいたい2進90桁)Python3 int型を使っていましたが、
x = ar + (br - ar) * modinv(a,b) % b * a
x = x + (cr - x % c) * modinv(a,c) % c * modinv(b,c) % c * a * b
このうちa,b,c,ar,br,crは31bitにおさまる数を使っているので、2行目の一番右のbを乗算するまでは確実に64bit整数の範囲内におさまります。ここでCUDAには__umul64hiという64bit整数×64bit整数の上位桁を計算する命令があるので、これを使うことで計算結果をulong型変数2つに余裕で格納することができます。
また、繰り上がり計算もGPUで並列計算しています。出力配列は1要素あたり32bitなので、Garnerで2進90桁を復元したら0-31桁、32-63桁、64-95桁と分割して各要素に加算します。
uint lastE3_1 = atomicAdd( &arrayE3[idx+1], ui32_64 );
ここではuint型のarrayE3[idx+1]にui32_64を加算したいという状況です。普通に加算処理を書くと、他のスレッドからもarrayE3[idx+1]にアクセスがあるのでデータ競合の問題が発生してしまいます。なのでここはAtomic演算を使って排他アクセスします。またatomicAddは加算前のarrayE3[idx+1]に入っている値を返してくれます。加算後の値というのは返って来ず、uint型でオーバーフローしたかもすぐには分かりません。ただ加算前の値+加算したい値はスレッド内でも計算できるので、arrayE3[idx+1]自体で繰り上がりが発生したかは判定できます(これはソースを見たほうが早いかもしれません)。そうしたらarrayE3[idx+2]に対してAtomic演算で加算処理しまたそこで繰り上がったらarrayE3[idx+3]に・・・といった処理をしていけば良いです。繰り上が続いていく確率は非常に低いので1スレッドあたり3,4回のAtomic演算で処理を終わらせることができます。Atomic演算自体はランダムアクセス程度の速度なので極端に遅くなる心配もないです。
また、CUDAでなくOpenCLでもmulhi命令やAtomic演算は扱えます。
さてそれでは速度比較をしたいと思います。
5 速度比較
5-1 Python vs CUDA
A,B=$2^N$桁(4294967296進数)
として
$C=A×B$
をCPU,GPUで計算して速度を測ります。
fmt_smaple4.py vs fmt_smaple5.pyをやっている感じです。
計測したところはA,Bのデータがデバイス(CPU,GPU)に確保された状態から、繰り上がり処理が完了したところまでです。
実行環境
CPU:core i9 9920X
RAM:DDR4 3600Mhz 16G*4 クアッドチャネル
GPU:RTX 2080Ti
処理時間(msec)
| N | Python | PyCUDA |
|---|---|---|
| 2 | 2.636432648 | 2.030849457 |
| 3 | 5.752801895 | 0.997066498 |
| 4 | 11.19756699 | 0.999450684 |
| 5 | 16.37482643 | 0.985145569 |
| 6 | 31.54706955 | 0.997781754 |
| 7 | 81.0508728 | 1.992464066 |
| 8 | 188.5592937 | 1.996278763 |
| 9 | 445.4622269 | 2.000808716 |
| 10 | 1047.091961 | 1.92117691 |
| 11 | 2431.799173 | 2.991437912 |
| 12 | 5611.189127 | 2.968549728 |
| 13 | 12762.6946 | 3.026247025 |
| 14 | 28899.42575 | 2.991199493 |
| 15 | 64907.24063 | 3.007650375 |
| 16 | 145894.0177 | 2.97832489 |
| 17 | 326845.052 | 4.023790359 |
| 18 | 732387.6169 | 8.923768997 |
| 19 | 1558503.907 | 16.954422 |
| 20 | 3391695.763 | 30.91740608 |
| 21 | 7350215.919 | 58.69293213 |
| 22 | 16059278.7 | 120.541811 |
| 23 | 34747664.01 | 222.6142883 |
| 24 | 75119683.56 | 473.2966423 |
| 25 | 161561500 | 940.9193993 |
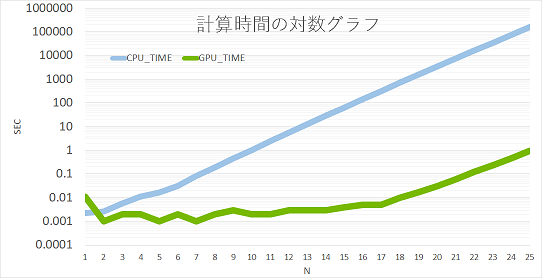
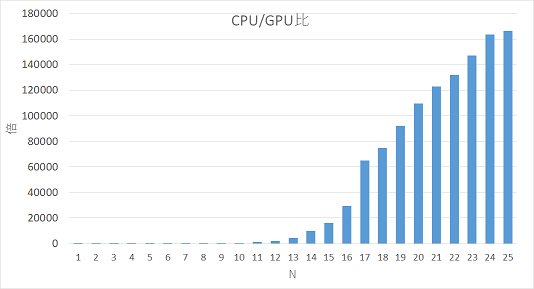
な、なんということでしょう!最大で__16万倍__以上も高速化できました。$N=25$ではCUDAで0.94secに対しPythonで161000secかかっており歴然たる差です。GPGPU最高!!!
(定数倍高速化に目が行きがちですが、ちゃんとNが増えるにつき計算時間が2.3-4倍になっているところも注目です。)
正直なところここまで差がついたのは、私の書いたPythonコードが最適化されてないというのも大きいと思っています。無駄な型変換とか多い気がするし(追記1:コメント頂きpow関数使って2.6倍高速化できました)。もちろんCPU,GPUのハード性能の差も大きいはずです。インタプリタ言語特有の遅さみたいなのもありそうですし。なんだかいろんな要素が積み重なって16万倍の差につながっているようなので、まずはC++でも測ってみましょう。
5-2 Python vs C++ vs CUDA
処理時間(msec)
| N | Python | C++ | PyCUDA |
|---|---|---|---|
| 2 | 2.6 | 20 | 2 |
| 3 | 5.8 | 8 | 1 |
| 4 | 11 | 7 | 1 |
| 5 | 16 | 24 | 1 |
| 6 | 32 | 9 | 1 |
| 7 | 81 | 9 | 2 |
| 8 | 189 | 9 | 2 |
| 9 | 445 | 21 | 2 |
| 10 | 1047 | 20 | 2 |
| 11 | 2432 | 33 | 3 |
| 12 | 5611 | 81 | 3 |
| 13 | 12763 | 144 | 3 |
| 14 | 28899 | 290 | 3 |
| 15 | 64907 | 656 | 3 |
| 16 | 145894 | 1456 | 3 |
| 17 | 326845 | 3255 | 4 |
| 18 | 732388 | 7183 | 8.9 |
| 19 | 1558504 | 15912 | 16.95 |
| 20 | 3391696 | 35121 | 30.92 |
| 21 | 7350216 | 77173 | 58.69 |
| 22 | 16059279 | 168893 | 120.5 |
| 23 | 34747664 | 367561 | 222.6 |
| 24 | 75119684 | 798197 | 473.3 |
| 25 | 161561500 | 1727122 | 940.9 |
Python vs C++で約90倍、C++ vs CUDAで約1800倍の差がつきました(C++はgcc -O3でコンパイル)。インタプリタ言語とコンパイラ言語の差もすごいです。こんなもんなんですかね?せいぜい10倍くらいの差かと思っていましたが。
ここで多倍長乗算の処理のうち何の処理が一番計算時間を占めているか気になったので計測してみました。C++での計算時間を参考にしています。
これを見ると計算時間のほとんどがFMT順変換と逆変換であることが分かります。いくら$O(NlogN)$のオーダーといえど二重ループになっているところであり、やはり重いですね。二重ループ内の処理はメモリアクセス(ランダムアクセス)と64bit整数の剰余計算がメインなのでそのどちらかが律速になっていると睨みました。そこでべき剰余だけを2倍量計算するコードでC++で計測してみたところ計算時間が約2倍になりました。つまりべき剰余の演算律速だったということです。
ボトルネックはおおむね特定できたので、先ほどのC++ vs CUDAの速度差についても考えてみたいと思います。現在1コア1スレッドSIMD化なしのC++プログラム vs CUDAという構図になっています。これではあまりにもCPUコード側が不利なので、CPU全コアフル稼働&SIMD化したらどこまで速くなるか気になります。
ところで剰余計算ってSIMD化でどこまで速くなるんですかね・・?除数が固定なら剰余が乗算に置き換えられてどうこうなると聞いたことがあるようなないような(追記1:剰余を乗算やビット演算に置き換えるのをモンゴメリ乗算というそうです。)
5-3 C++ vs OpenCL(on CPU)
CPUフル稼働できて私が使えるのはOpenCLしかないのでこれを使います。OpenCLはAMDのGPUでGPGPUやる時に登場しがちですが、CPU上でも動きます。私の経験ですがCPU上で動かしたときもかなり性能を引き出してくれる印象がありますので、性能比較で遊ぶにはもってこいです。
さっそく遊んでみましょう!
処理時間(msec)
| N | OpenCL(i9 9920X) | C++ |
|---|---|---|
| 2 | 0 | 20 |
| 3 | 1 | 8 |
| 4 | 0 | 7 |
| 5 | 1 | 24 |
| 6 | 1 | 9 |
| 7 | 1 | 9 |
| 8 | 1 | 9 |
| 9 | 2 | 21 |
| 10 | 4 | 20 |
| 11 | 5 | 33 |
| 12 | 5 | 81 |
| 13 | 7 | 144 |
| 14 | 9 | 290 |
| 15 | 14 | 656 |
| 16 | 28 | 1456 |
| 17 | 55 | 3255 |
| 18 | 113 | 7183 |
| 19 | 240 | 15912 |
| 20 | 513 | 35121 |
| 21 | 1112 | 77173 |
| 22 | 2412 | 168893 |
| 23 | 5240 | 367561 |
| 24 | 11355 | 798197 |
| 25 | 24500 | 1727122 |
OpenCLはC++の70倍高速という結果です。i9 9920Xは12コアなので1コアあたりでも6-7倍高速化したことになります。これはSIMDの何がどう効いたのか良くわかりませんが・・・。(整数も早くなるんですかね)
5-4 OpenCL(on GPU) vs CUDA
せっかくなので同じ土俵でOpenCL vs CUDAの因縁の対決をやってみましょう。RTX2080Ti上でOpenCLとCUDAを動かしたときの速度はこうなりました。
処理時間(msec)
| N | OpenCL(RTX2080Ti) | PyCUDA(RTX2080Ti) |
|---|---|---|
| 2 | 1 | 2 |
| 3 | 0 | 1 |
| 4 | 1 | 1 |
| 5 | 1 | 1 |
| 6 | 1 | 1 |
| 7 | 1 | 2 |
| 8 | 1 | 2 |
| 9 | 1 | 2 |
| 10 | 1 | 2 |
| 11 | 1 | 3 |
| 12 | 1 | 3 |
| 13 | 2 | 3 |
| 14 | 1 | 3 |
| 15 | 2 | 3 |
| 16 | 3 | 3 |
| 17 | 4 | 4 |
| 18 | 6 | 9 |
| 19 | 13 | 17 |
| 20 | 26 | 31 |
| 21 | 54 | 59 |
| 22 | 113 | 121 |
| 23 | 242 | 223 |
| 24 | 435 | 473 |
| 25 | 930 | 941 |
ほんのわずかOpenCLのほうが速そうに見えますが。なんとなく引き分けでいいような気がします。
またOpenCLの結果からCPU(i9 9920X)とGPU(RTX2080Ti)の性能差が25倍くらいだということも分かりました。もちろんこの性能差というのは今回のプログラムに関してのみ言えることで、処理内容によっていくらでも変わりうるものです。
というわけでまとめると、16万倍の内訳は
Python vs C++ : コンパイラ言語の壁で__90倍__高速化
C++ vs OpenCL(on CPU) : マルチスレッド&SIMD化で__70倍__高速化
CPU vs GPU : ハードウェア性能差で__25倍__高速化
になります。
5-5 べき乗余のテーブル生成、参照で2~5倍高速化(2020/1追記分)
これまで二重ループ内のべき乗余$ω^{i}$を逐一計算してましたが、あらかじめ計算した配列を用意して参照するようにします。これでC++で5倍、PyCUDAで2倍速くなりました。
ソースはこちら
PyCUDA:https://github.com/toropippi/FMT_QiitaSample/blob/master/fmt_smaple6_qiita.py
OpenCL:https://github.com/toropippi/FMT_QiitaSample/tree/master/%E9%80%9F%E5%BA%A6%E6%AF%94%E8%BC%83%E7%94%A8OpenCL
C++:https://github.com/toropippi/FMT_QiitaSample/blob/master/%E9%80%9F%E5%BA%A6%E6%AF%94%E8%BC%83%E7%94%A8C%2B%2B/fmt_table.cpp
| N | C++テーブル参照なし | C++テーブル参照あり |
|---|---|---|
| 2 | 20 | 0 |
| 3 | 8 | 0 |
| 4 | 7 | 0 |
| 5 | 24 | 0 |
| 6 | 9 | 0 |
| 7 | 9 | 1 |
| 8 | 9 | 1 |
| 9 | 21 | 2 |
| 10 | 20 | 4 |
| 11 | 33 | 9 |
| 12 | 81 | 19 |
| 13 | 144 | 40 |
| 14 | 290 | 84 |
| 15 | 656 | 175 |
| 16 | 1456 | 369 |
| 17 | 3255 | 775 |
| 18 | 7183 | 1639 |
| 19 | 15912 | 3445 |
| 20 | 35121 | 7436 |
| 21 | 77173 | 15656 |
| 22 | 168893 | 32999 |
| 23 | 367561 | 72912 |
| 24 | 798197 | 174132 |
| 25 | 1727122 | 380685 |
| N | OpenCL(CPU)テーブル参照なし | OpenCL(CPU)テーブル参照あり |
|---|---|---|
| 2 | 0 | 0 |
| 3 | 1 | 0 |
| 4 | 0 | 1 |
| 5 | 1 | 1 |
| 6 | 1 | 1 |
| 7 | 1 | 1 |
| 8 | 1 | 1 |
| 9 | 2 | 1 |
| 10 | 4 | 2 |
| 11 | 5 | 3 |
| 12 | 5 | 3 |
| 13 | 7 | 3 |
| 14 | 9 | 4 |
| 15 | 14 | 5 |
| 16 | 28 | 7 |
| 17 | 55 | 12 |
| 18 | 113 | 19 |
| 19 | 240 | 35 |
| 20 | 513 | 74 |
| 21 | 1112 | 152 |
| 22 | 2412 | 323 |
| 23 | 5240 | 765 |
| 24 | 11355 | 2106 |
| 25 | 24500 | 4884 |
| N | PyCUDAテーブル参照なし | PyCUDAテーブル参照あり |
|---|---|---|
| 2 | 2 | 0 |
| 3 | 1 | 1 |
| 4 | 1 | 1 |
| 5 | 1 | 2 |
| 6 | 1 | 1 |
| 7 | 2 | 1 |
| 8 | 2 | 1 |
| 9 | 2 | 2 |
| 10 | 2 | 2 |
| 11 | 3 | 2 |
| 12 | 3 | 2 |
| 13 | 3 | 3 |
| 14 | 3 | 2 |
| 15 | 3 | 3 |
| 16 | 3 | 3 |
| 17 | 4 | 3 |
| 18 | 9 | 4 |
| 19 | 17 | 5 |
| 20 | 31 | 10 |
| 21 | 59 | 21 |
| 22 | 121 | 47 |
| 23 | 223 | 104 |
| 24 | 473 | 226 |
| 25 | 941 | 536 |
6 ガウス=ルジャンドルのアルゴリズムで円周率を3億桁計算
いよいよ円周率を計算してみましょう。アルゴリズムはガウスルジャンドルwikiを使います。乗算以外に除算や平方根の計算がでてきますが、これはニュートン法を使えば良いです。
出力は16進数でtxtに出力とします。10進数は基数変換が大変そうなので次回以降実装とします。
ソースはこちら
https://github.com/toropippi/FMT_QiitaSample/blob/master/CalcPI_GPGPUfmt.py
| 4294967296進数N桁 | 10進数N桁 | 計算時間(sec) |
|---|---|---|
| 1024 | 9864.150898 | 1.105081319 |
| 2048 | 19728.3018 | 1.332427501 |
| 4096 | 39456.60359 | 1.591748238 |
| 8192 | 78913.20718 | 1.945914745 |
| 16384 | 157826.4144 | 2.207063675 |
| 32768 | 315652.8287 | 2.728562117 |
| 65536 | 631305.6575 | 3.273030281 |
| 131072 | 1262611.315 | 4.13736844 |
| 262144 | 2525222.63 | 5.635286331 |
| 524288 | 5050445.26 | 8.3940575 |
| 1048576 | 10100890.52 | 13.05427217 |
| 2097152 | 20201781.04 | 24.9399969 |
| 4194304 | 40403562.08 | 48.619494 |
| 8388608 | 80807124.16 | 98.77346897 |
| 16777216 | 161614248.3 | 190.9101679 |
| 33554432 | 323228496.6 | 423.4236162 |
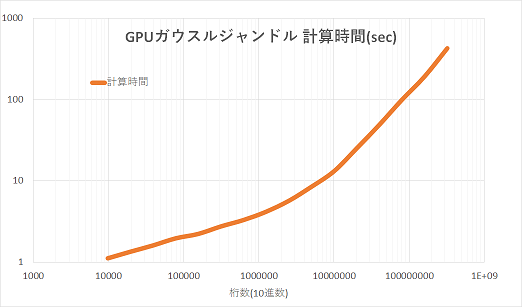
だいたい円周率3億桁計算するのにGPUを使って420秒かかっています。y-cruncherだとCPUで10億桁200秒程度らしいのでまだまだですね・・。
アルゴリズム的にはy-cruncherが採用しているChudnovskyの公式が最速らしいのでガウスルジャンドルをそれに変えれば少しは速くなるでしょうか・・・?ただその場合binary splittingをどうGPUに最適化するかという問題になりそうです。というかなりました。それで挫折して今回ガウスルジャンドルを使った形です。
あとこのプログラムでは剰余計算が律速になっているようなのでそこをなんとか高速化したらもう少しy-cruncherに喰らいつけるのでは・・と思案してます。できるかもわかりませんが・・。
追記1:モンゴメリ乗算の愚直実装で1.2倍高速化できました。1.2倍・・・あまり速くならなかったけどこれ元々コンパイラが剰余をモンゴメリ乗算に展開してた可能性もある?
追記2:べき乗余テーブル参照にして2倍速くなりました(5-5に追記)
7 最後に
最後までお付き合い頂きありがとうございます。
実はFMTのGPU実装は6年前から挑戦していたのですが色んなポイントで挫折していました。6年も経てばQiita含め参考記事もいろいろ増えていて私自身、色んな面で助けられました。一方FMTで多倍長に挑戦した記事はあまりないように思い、同じことをやろうとしている人に少しでも役に立てばと思って記事にしてみました。単に多倍長の計算をするならGMPを使えばいいですが(それもそれで面白そうですが)、やはりGPUで計算するロマンと自分で実装する楽しさは何にも勝るため、何としてでも完成させてよかったです。参考にしてほしい反面、間違ったことを書いてるとそのまま広まってしまうのではという恐怖もあります。もし内容で気になったことがあればコメント頂ければ幸いです。
次回は未定です。
8 追加の参考文献とか
円周率jpのぺージ
http://xn--w6q13e505b.jp/
個人ブログ。C++実装コードあり
https://math314.hateblo.jp/entry/2015/05/07/014908
個人ブログ?C++実装コードあり
https://lumakernel.github.io/ecasdqina/math/FFT/NTT
個人ブログ。Python実装コードあり
https://smijake3.hatenablog.com/entry/2017/01/04/042136
https://tjkendev.github.io/procon-library/cpp/fft/fmt.html
ニュートン法で逆数と平方根を求める
http://www.finetune.co.jp/~lyuka/technote/fract/sqrt.html
モンゴメリ乗算
https://ikatakos.com/pot/programming_algorithm/number_theory/montgomery_multiplication